基于MATLAB的自动推料机构多目标优化设计
周 昇
(南通职业大学 机械工程学院,江苏 南通226007)
自动推料机构属于多杆机构,用传统的方法设计多杆机构时,先要初步确定多杆机构的部分结构参数,接着进行计算其它结构参数,如果所得结果不符合设计要求,以上过程要重复进行,直至满足设计要求。因此用传统的方法设计多杆机构,设计时间长,工作量大,而且设计结果不一定是最优的设计[1]。如果能建立多杆机构优化设计的数学模型,并且将多杆机构的基本结构参数(杆长、节点坐标)作为设计变量,体积最小和效率最高作为目标函数,运动连续性和空间结构等要求作为设计约束条件,运用MATLAB编制多杆机构优化设计程序,就可以方便快速计算出符合设计要求且体积最小效率率最高的自动推料机构。
1 多目标优化和fm incon函数[3]
在工程实际问题中,如果同时要求两个或两个以上目标函数达到最优值,就称为多目标优化设计问题。多目标优化设计数学模型的表达式为:
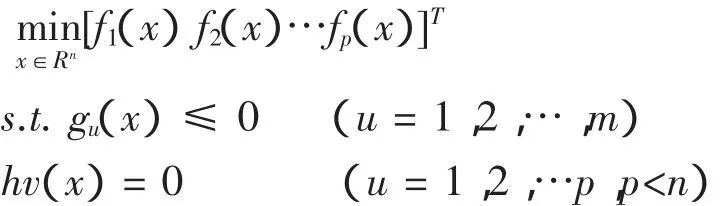
多目标优化问题求解的方法主要是构建合适的评价函数。评价函数是由单目标函数组合而成的。单目标函数的求解可以用MATLAB优化工具箱中的函数fmincon来实现,其调用格式为:
[x,fval]=fmincon(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon)
2 建立自动推料机构优化设计的数学模型
如图1为自动推料机构,它的主体机构是六杆机构,这个六杆机构是由一个曲柄摇杆机构和一个摇杆滑块机构串联组成。曲柄1铰接在机架6的A点,连杆A一端与曲柄1铰接,另一端与摇杆3在C点铰接,摇杆3与机架6在D点铰接,连杆B一端与摇杆在E点铰接,另一端与滑块5在F点铰接,滑块5与机架用移动副连接。曲柄1绕A点转动,连杆A带动摇杆3绕D点摆动,连杆B带动滑块5沿机架6上的轨道往复移动。构件的长度AB、AD、BC、CE、ED、EF,偏距e是机构的基本结构参数,可将它们作为设计变量,所以一共是7个变量。变量基本尺寸如表1所示。
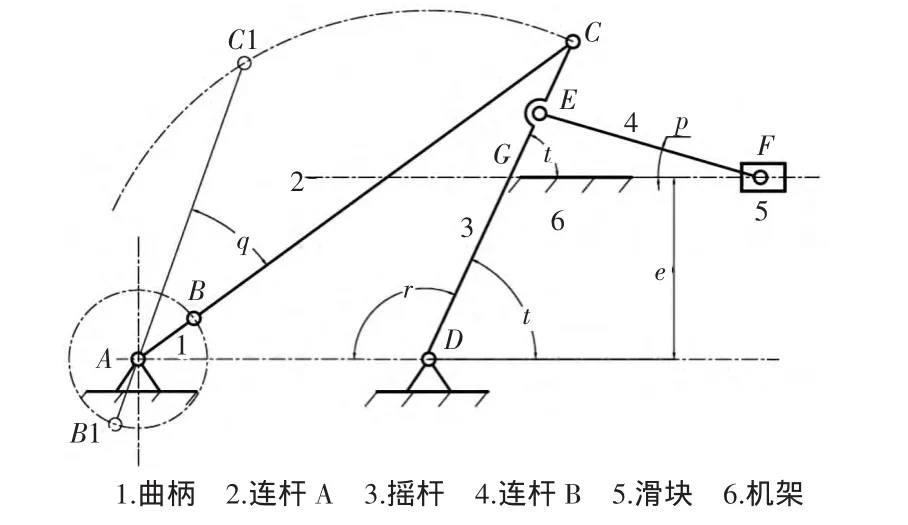
图1 自动推料机构
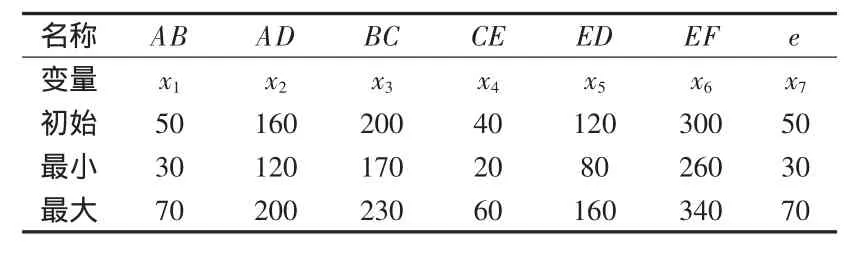
表1 自动推料机构基本尺寸
曲柄摇杆机构的急回特性系数为k=1.2,图1画出了曲柄运动的两个极限位置(曲柄和连杆A重合在一条线上),角度q为极位夹角。

滑块的行程为100 mm.
2.1 自动推料机构优化设计的设计变量
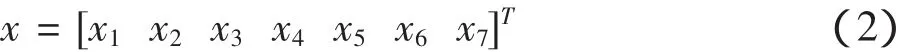
2.2 自动推料机构优化设计的目标函数
目标函数主要反映机构工作时的经济成本,当连杆B与水平线夹角P即压力角最小时机构阻力最小工作效率最高,所以可将压力角设定为一个目标函数 f1(x).
在现位置时,连杆B摆动到最高点,此时压力角p获得向上的最大值p1,此时r为r1,根据余弦定理:
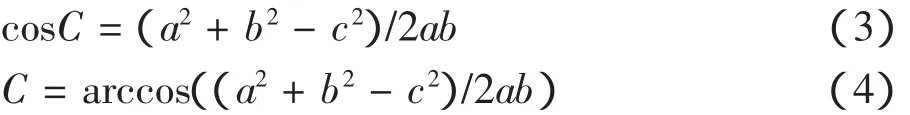
为叙述简单,将(4)式编成函数
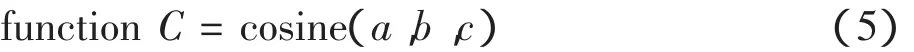
(见后面程序),所以在△ADC中有:
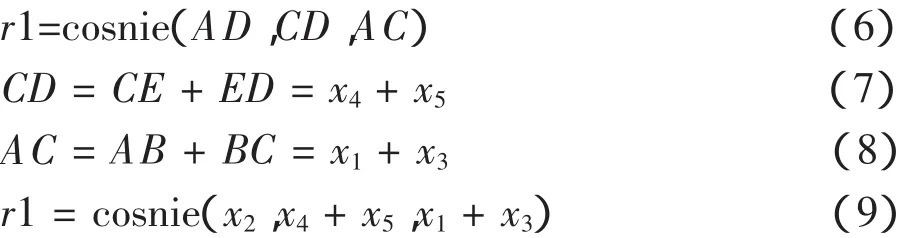
根据正弦定理,在△EFG中有:

B点移动到B1位置时,连杆B摆动到最低点,此时压力角p获得向下的最大值p2,此时r为r2,对比上面此时在△ADC中:

另一个目标函数放f2(x)设定为机构的总体尺寸(机构宽度×长度)最小。


2.3 自动推料机构设计的约束条件
2.3.1 非线性不等式约束
在由AB、BC、CD、AD组成的曲柄摇杆机构中要实现正常的曲柄摇杆运动,AB应为最短杆,即AB 2.3.2 非线性等式约束 整个机构要满足行程要求,即 因为r= π -t而 cos(π-a)=-cos a所以 必须符合k=1.2的急回特性 根据余弦定理,在△ADC中有: 2.4.1 主运行程序 %脚本main %定义起始点 x0=[50 160 200 40 120 300 50] %定义函数自变量的下界 l b=[30 120 170 20 80 260 30] %定义函数自变量的上界 ub=[70 200 230 60 160 340 70] %调用函数fmincon [x,fval,exitflag,output]=fmincon(@objfun,x0,[],[],[],[],lb,ub,@confun) x,fval,exitflag,output 2.4.2 已知三边求角函数cosnie(余弦定理) %编写余弦定理函数cosnie function C=cosine(a,b,c) C=a cos((a2+b2-c2)/(2×a×b)) end 2.4.3 目标函数objfun %编写目标函数objfun function f=objfun(x) r1=cosine(x(2),x(4)+x(5),x(1)+x(3));%调用余弦函数 p1=a sin(( x(5)× sin(r1)-x(7))/x(6)) f1=abs(p1) r2=cosine(x(2),x(4)+x(5),x(3)-x(1)) p2=a sin(( x(5)× sin(r2)-x(7))/x(6)) if abs(p2)>abs(p1) f1=abs(p2);end f1=57.3×f1 f2=(x(2)+x(6))×(x(1)+x(3)) f=f1×105+f2 end 2.4.4 约束的函数confun %编写描述非线性等式和不等式约束的函数 function[c q]=confun(x) %非线性不等式约束 c(1)=x(1) -x(2) c(2)=x(1) -x(3) c(3)=x(1) -x(4)-x(5) c(4)=x(2) -x(3) c(5)=x(4) +x(5)-x(3) c(6)=x(1) +x(3)-x(2)-x(4) -x(5) c(7)=x(7)-x(4)-x(5) %非线性等式约束 r1=cosine(x(2),x(4)+x(5),x(1)+x(3)) p1=asin(( x(5)× sin(r1)-x(7))/x(6)) r2=cosine(x(2),x(4)+x(5),x(3)-x(1)) p2=asin(( x(5)×sin(r2)-x(7))/x(6)) q(1)=x(5)×(cos(r2)-cos(r1))+x(6)×(cos(p1)-cos(p2))-100 q1=57.3×cosine(x(2),x(1)+x(3),x(4)+x(5)); q2=57.3×cosine(x(2),x(3)-x(1),x(4)+x(5)); q(2)=q2-q1-16.36; end 运行程序后可得: x=57 176 195 20 80 260 62 将优化前后进行对比建立表2,从表2可以看出,经过优化设计后的自动推料机构由于p的减小,连杆B差不多一直保持在水平状态,因此工作阻力减少,整个机构的工作效率提高,驱动曲柄的电动机功率减少了35%.同时自动推料机构所占空间也减少了8%,优化的效果是非常明显的。 表2 自动推料机构优化前后对比表 综上所述,基于MATLAB优化工具箱的机构设计方法,在满足使用要求,保证使用性能的前提下,与传统设计方法比较,可以设计出体积较小,效率较高的自动推料机构,同时也节省设计时间、减小设计难度,是对传统设计的重大改进。经验也同时证明,用MATLAB优化工具箱求解机械机构的优化问题,是非常明智的选择。 [1]孙开元.常见机构设计及应用图例[M].北京:化学工业出版社,2013:20-21. [2]赵继俊.优化技术与MATLAB优化工具箱[M].北京:机械工业出版社,2011:166-171. [3]李万祥.工程优化设计与MATLAB实现[M].北京:清华大学出版社,2010:251-259. [4]秦大同.机构设计[M].北京:化学工业出版社,2014:61-70.
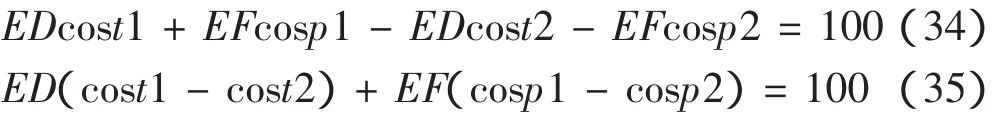


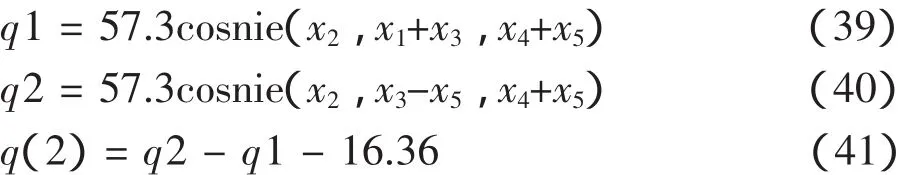
2.4 自动推料机构优化设计的MATLAB代码[3]

3 结束语

