城市商业银行经济资本及风险管理研究

李淑锦，吕 全

(杭州电子科技大学 经济学院，浙江 杭州310018)

经济资本是用来减缓风险冲击和保持正常经营的资本。自巴塞尔协议颁布以来，经济资本管理体系在各大商业银行得到深入的应用。然而，随着我国加入WTO，国内金融市场逐渐对外开放，银行面临的风险越来越大，风险种类越来越复杂，各类风险事件层出不穷，如浙江省温州市频频传出民间借贷资金链断裂，企业主跑路的消息，同时，省内光伏行业也曾出现大面积的倒闭潮。这预示着信贷集中的负面影响开始凸显，商业银行经济资本的管理面临新的挑战。

国内学者已经注意到我国银行信贷风险集中的问题，如褚应前和秦海坤(2002)［1］通过对靖江市内中国工商银行等五家大型国有商业银行的调研和分析，指出银行前十大客户贷款占各项贷款的比重较高，且呈上升趋势。赵宇翔(2008)［2］利用2002—2006年山东省银行的数据，构建基于违约率的风险集中度模型，定量分析了山东省银行业的信贷风险集中情况。

关于经济资本，2006年发布的新《巴塞尔协议Ⅱ》［3］的内部评级法介绍了信用风险最低经济资本的度量方法，其理论基础是渐进单因子模型(ASRF 模型)，2010年的《巴塞尔协议Ⅲ》从监管的角度对银行资本的质量和数量提出更高的要求，但仍然沿用之前的内部评级法度量最低经济资本。Goody(2003)［4］认为ASRF 模型假设过于苛刻，此后国内外学者对经济资本计量方法进行了调整。Pykhtin(2004)［5］首次将ASRF 模型扩展为多因子模型，使用各个部门的系统风险因子来描绘不同部门的系统风险，以此来解决存在行业集中风险时ASRF 模型低估经济资本的问题;在多因子模型的基础上，Cespedes(2006)［6］构建扩散因子，提出了扩散因子模型。国内，姚奕和杜音颖(2007)［7］解读了银行所需资本的计提公式和计提方法;杨继光和刘海龙(2009)［8］、秦学志(2012)［9］通过梳理国外学者使用的多因子模型、二项式扩展技术和扩散因子模型，介绍这三种模型的计算方法及其应用范围，但仅仅停留在理论上的公式推导，没有使用银行数据进行具体分析。

从目前国内对经济资本的研究现状看，理论多于实证，对大型国有银行的研究多于对中小商业银行的研究。由于城市商业银行有其自身发展的优劣势，在其信贷组合中常常存在信贷集中风险，因此本文重点研究城市商业银行的经济资本计量问题。首先以代表性的宁波银行为例，分析了其信贷集中风险问题，然后利用二项式扩展技术对北京银行和宁波银行的经济资本进行测算，以期从量化的角度指导城市商业银行加强风险管理，提高抗风险的能力。

一、城市商业银行信贷风险集中度的现状

商业银行的信贷风险集中度分为客户集中度、行业集中度以及传染集中度三种。学术界主要采用HHI 指数方法来计量信贷组合的客户集中度;行业集中度是计量贷款组合的行业或地区不均匀分布产生的风险，如果用RCα表示α 行业的行业集中度，可以利用下面的公式(1)度量。

具体的指标见李淑锦和吕全(2013)［10］。传染集中度是计量由于双边交易关系而相互关联企业的贷款集中所产生的风险，由于其度量涉及到的变量较多，计算方法复杂，数据难以收集，本文在研究经济资本配置时忽略了该集中度风险。

为了说明我国城市商业银行信贷风险集中现状，本部分仅以宁波银行的情况加以说明。利用宁波银行2008—2013年的信贷数据，用HHI 指数对客户集中度进行测算，结果显示，在此期间宁波银行信贷投放于前十大客户的比重不大，HHI 指数值较小，且存在逐年下降的趋势，说明其客户集中风险较小。

根据公式(1)测算了2008—2013年宁波银行信贷组合的行业集中度，具体的结果见李淑锦和吕全(2013)［10］。结果发现在2008—2013年宁波银行信贷投放主要集中在制造业、租赁和商务服务业、批发和零售业以及房地产业，其行业集中度水平一直较高，采矿业，公共管理、社会保障和社会组织以及文化、体育和娱乐业等行业的集中度水平始终较低，充分说明我国城市商业银行信贷资产存在行业集中的风险。

二、经济资本的计量模型

经济资本是商业银行为了管理信贷风险而需要的一种资本，银行必须确保拥有充足的经济资本以预防非预期的损失。新《巴塞尔协议》的主要创新就是利用内部评级法中的渐进单因子模型来计算商业银行的经济资本。

(一)渐进单因子模型

该模型做了两个关键假设:(a)银行信贷组合是无限粒度的;(b)只有一个系统风险来源。在特殊风险因子独立以及(a)与(b)假设下，经济资本的计算公式为

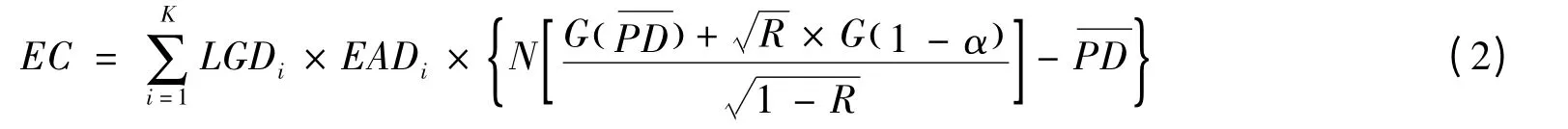
其中，EADi表示第i 笔贷款的违约暴露，LGDi表示第i 笔贷款的违约损失率，N 和G 分别表示标准正态分布的分布函数及其反函数，是信贷资产平均违约概率，K 是信贷资产数目，1－α 为置信水平，而

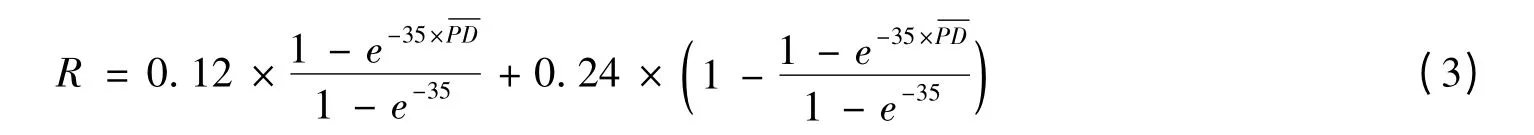
表示组合中资产的平均相关系数。

由模型的两个假设可知，ASRF 模型没有把信贷集中风险纳入其中考虑。

(二)二项式扩展技术

当银行的信贷组合存在行业集中度风险时，对经济资本的配置，学术界常用的理论模型主要有三种:多因子模型，扩散因子模型以及二项式扩展技术方法。多因子模型能准确地度量贷款组合因行业集中风险而需要额外计提的经济资本，但该模型计算复杂，且同ASRF 模型一样是基于渐进计算，比较适合大型国有银行;扩散因子模型也是在ASRF 模型的基础上计算调整后的经济资本，但需要通过模拟的方法获得扩散因子等参数，得到的结果也会存在精确度不高的问题;二项式扩展技术方法通过直接对银行的信贷资产进行划分和加总，更适合规模相对较小的、存在行业集中风险的银行对经济资本的计量，因此，本文选取二项式扩展技术作为城市商业银行的经济资本计量方法。

1．二项式扩展技术的基本原理

李红侠(2010)［11］介绍了二项式扩展技术，该方法假设信贷组合中的资产服从二项分布，且信贷组合中的资产具有同质性和独立性，即每个借款者拥有相同的违约率PD，风险暴露EAD 和违约损失率LGD，并且各借款者相互独立。然而，银行信贷组合中资产是彼此相关的。对此，需对资产池中的资产经过一定的处理，将其分为D 类，构造一个与原始资产池具有一致特征的理想化资产池，这样就可以使用二项式扩展技术计算出理想资产池的损失分布和经济资本，以理想资产池的经济资本代替现实的经济资本。计算过程中所涉及到的变量主要有行业相关系数、信贷资产池的分集评分D、各个行业的违约率以及违约损失率等。

2．二项式扩展技术的步骤

(1)违约率PD 的估计

信贷违约可以定义为在某一时期内无法足额归还银行贷款本金及利息的行为。有关违约率的计算，有历史数据统计法和市场数据期权法。根据新《巴塞尔协议》规定和我国银行业实际情况，本文将贷款逾期时间在3 个月以上的贷款和由于借款人财务状况恶化，或无力还款而对借款合同还款条款作出调整的那类重组贷款作为违约贷款。因此，违约率的计算公式可以简单地表示为:

(2)违约损失率LGD 的估计

违约损失率是指债务人一旦违约将给债权人造成的损失比例，反映的是贷款损失的严重程度。违约损失率的计算方法包括历史数据回归分析法、单风险因素模型估计法和β 分布估计法等。根据《巴塞尔资本协议》中内部评级初级法的规定，对非认定的抵押品担保的公司、主权和银行的高级债权的违约损失率值规定为45%，对非认定的抵押品担保的公司、主权和银行的次级债权的违约损失率值规定为75%，对于有满足巴塞尔委员会要求的抵押品抵押的贷款，可以根据委员会提供的公式(见公式5)来求得违约损失率。因此，只需对银行贷款资产的合理分类，就可以根据IRB 初级法求得违约损失率。

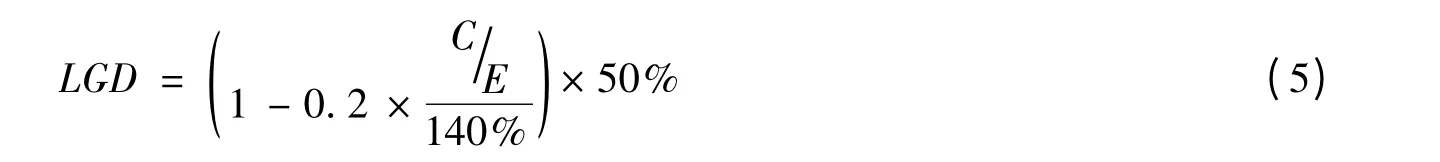
(3)行业相关系数

行业的相关性是影响风险集中度和经济资本的关键指标。估计行业相关性的方法主要有股票价格收益率、信贷违约率和资产收益率。Düllmann(2008)［12］的研究表明，由于违约率历史数据有向下偏斜的特点，用违约率数据来估计其相关性是不准确的，用资产收益的相关性来估计将更加有效。

(4)信贷资产池的分集评分

分集评分的原理是构造理想的资产组合，复制出原始资产池的违约损失情况。分集评分体现了原始资产池中各行业资产的风险集中程度。其计算公式为:

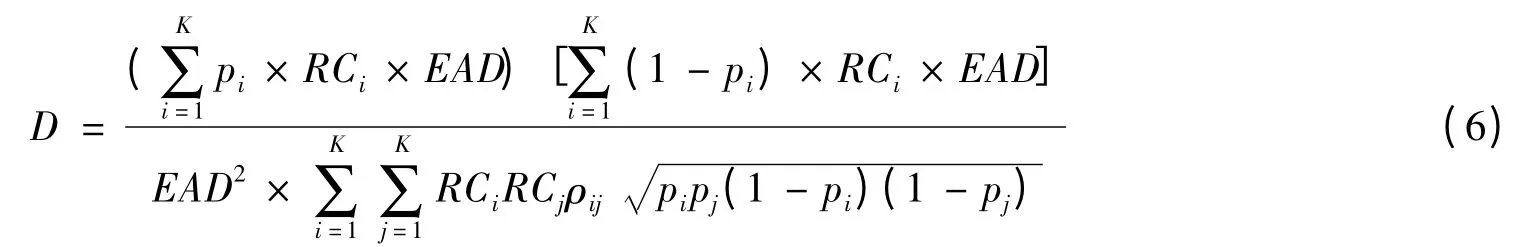
其中，RCi表示行业i 的风险集中度，pi表示行业i 的违约概率，ρij表示行业i 和行业j 之间的相关系数，EAD 表示违约暴露，K 为行业总数。

(5)理想资产池的违约分布及累积分布

在分集评分的基础上，得出理想资产池的违约分布及其累计分布，其基本计算公式为:

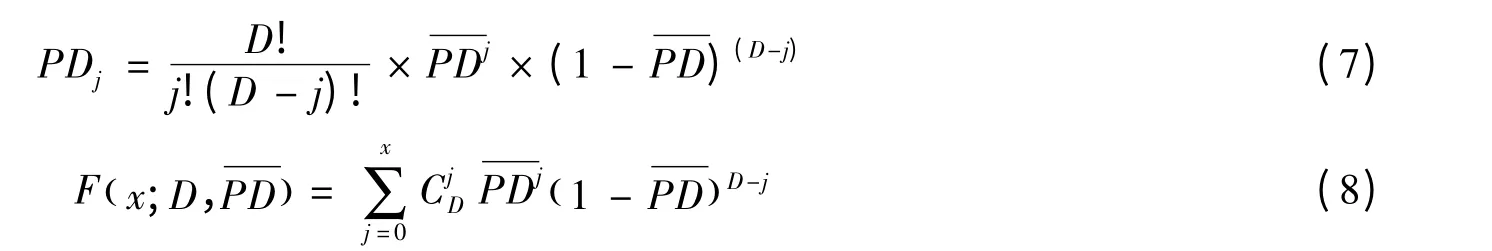
其中，PDj为D 类资产中有j 类同时违约的概率，是资产的平均违约概率。

(6)预期损失EL 和非预期损失UL

预期损失是银行预期在特定时期内资产可能遭受的平均损失EL;非预期损失是商业银行在一定的置信水平下最大损失超过预期损失值的部分，结合上文公式，可得非预期损失为:

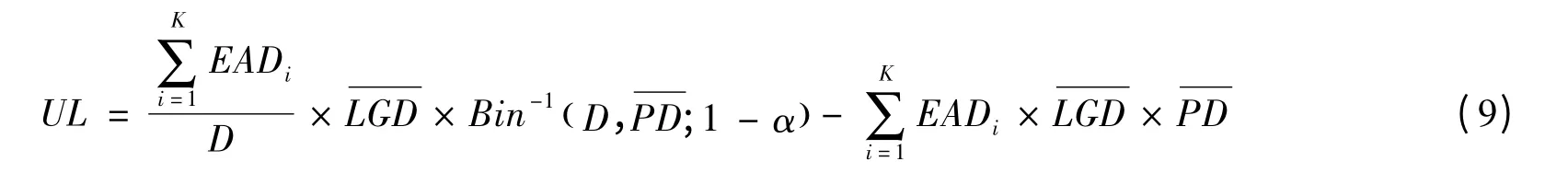
从以上公式中看出，非预期损失与分集评分D、行业风险集中度、违约暴露、违约概率以及违约损失率的大小有关。蒋建芳(2007)［13］认为非预期损失是损失分布的标准差，而经济资本是通过计量非预期损失得到的，那么抵消这种损失所要求的资本可以描述为经济资本。因此，本文同样以非预期损失作为经济资本的同义词，认为在风险的控制和监管上，非预期损失等于经济资本。

三、代表性的城市商业银行经济资本测算

(一)数据来源

1．研究对象和时间跨度的选择。本文选取宁波银行和北京银行作为研究对象，其资产规模处于城市商业银行的第一梯队，在当地具有较高的影响力，代表性较强。此外，宁波银行和北京银行属于上市公司，信息披露较完整，有利于进一步研究。本文选取的研究年份为两家银行上市之后若干年，即2008年至2013年。

2．行业的选取。本文按照国民经济行业分类标准对银行的贷款客户进行分类，选取贷款发放量最大的19 个行业(见表1)。

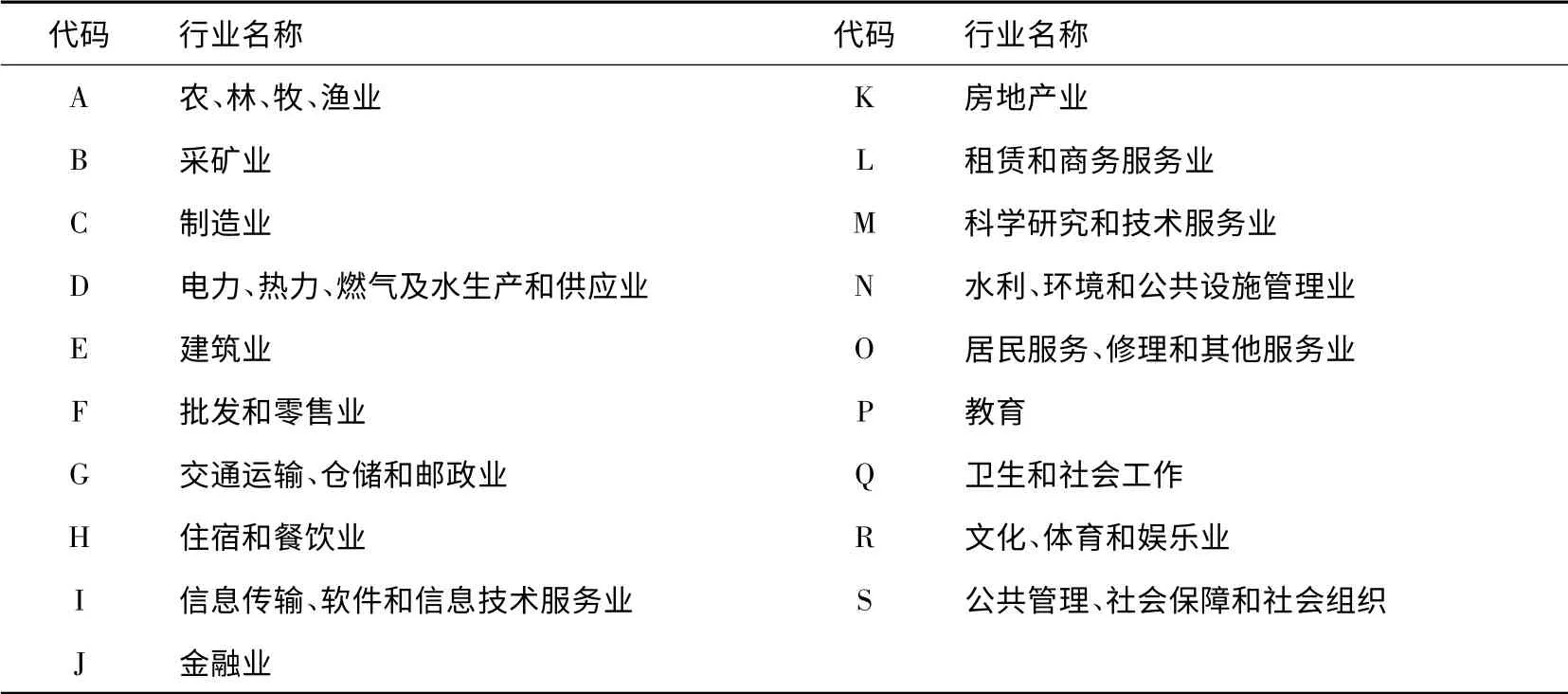
表1 商业银行贷款客户的主要行业分布

3．本文的数据来源包括2008年至2013年宁波银行和北京银行的年度报告和财务报表等披露的信息，《中国统计年鉴》，《中国金融统计年鉴》以及和讯财经等网站。

本文以2013年宁波银行和北京银行的真实贷款数据为样本，运用二项式扩展技术，测算两家银行平均违约概率，平均违约损失率，各行业的相关系数以及分集评分D，获得原始信贷资产池的损失分布，最终测算出2008年至2013年银行需要的经济资本。

(二)经济资本

1．平均违约率和平均违约损失率

信贷资产组合的平均违约率由各行业的违约率根据风险暴露比重加权平均获得，平均违约损失率根据银行贷款资产的抵押情况加权平均获得。利用公式(4)、(5)和两家银行年报披露的数据，计算出宁波银行2013年的平均违约概率为0.74%，平均违约损失率为0.503 3;北京银行2013年的平均违约概率为0.51%，平均违约损失率为0.571 5。

2．关于行业相关性

行业相关性是影响行业风险集中度的关键指标，本文采用资产收益率来度量行业相关性。结果表明，房地产业与住宿和餐饮业，教育与住宿和餐饮业、房地产业、水利、环境和公共设施管理业这几个行业之间的相关性相对较强，说明银行贷款行业的分布对风险分散作用较弱。

3．资产池的分集评分

由于城市商业银行信贷组合的行业集中度较高，而这些行业的相关性较强，所以本文采用分集评分的思想来构建理想资产池。根据公式(6)以及行业相关系数，计算得到宁波银行和北京银行信贷资产池的分集评分D 为9 和11。

4．理想资产池的违约分布及预期损失

运用二项式扩展技术测算理想资产池的信贷违约分布，进而计算资产池的损失分布。根据公式(7)和(8)，计算得到的理想资产池的违约损失以及信贷组合的预期损失如表2 和表3所示。因为理想资产池的损失分布近似代表了原始资产池的违约损失情况，这样，就可以根据理想资产池违约损失状况对原始资产池的信用质量做出判断。

例如，宁波银行的信贷资产均不发生违约的概率为93.5%，有一项发生违约的概率为6.31%，违约后的损失额度为41 600 万元，有2 项发生违约的概率为0.19%，违约后的损失额度为2 494 万元，有3项发生违约的概率为0.01%，违约后的损失额度约为65 万元，如此类推，测算出宁波银行的预期损失额为44 160 万元。同理，根据表3 可以得出北京银行的预期损失为119 017 万元。

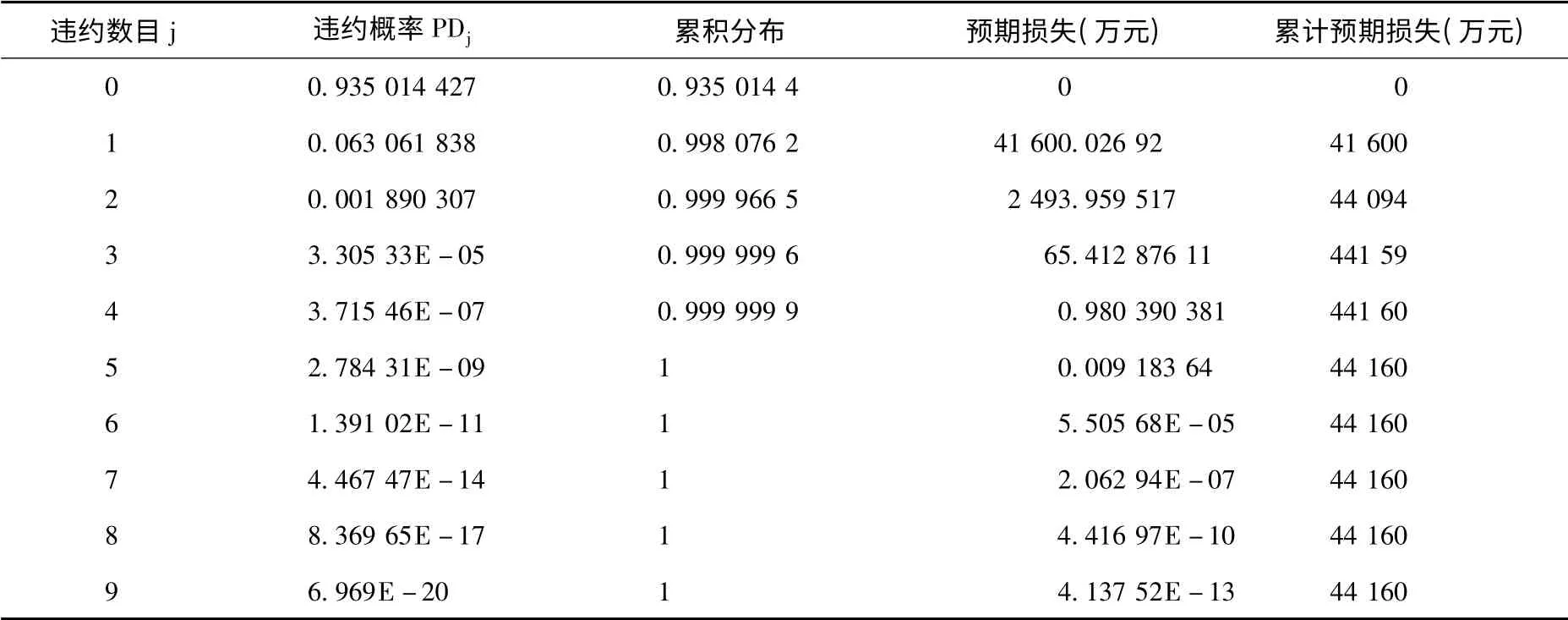
表2 宁波银行理想资产池的违约损失情况(2013年)

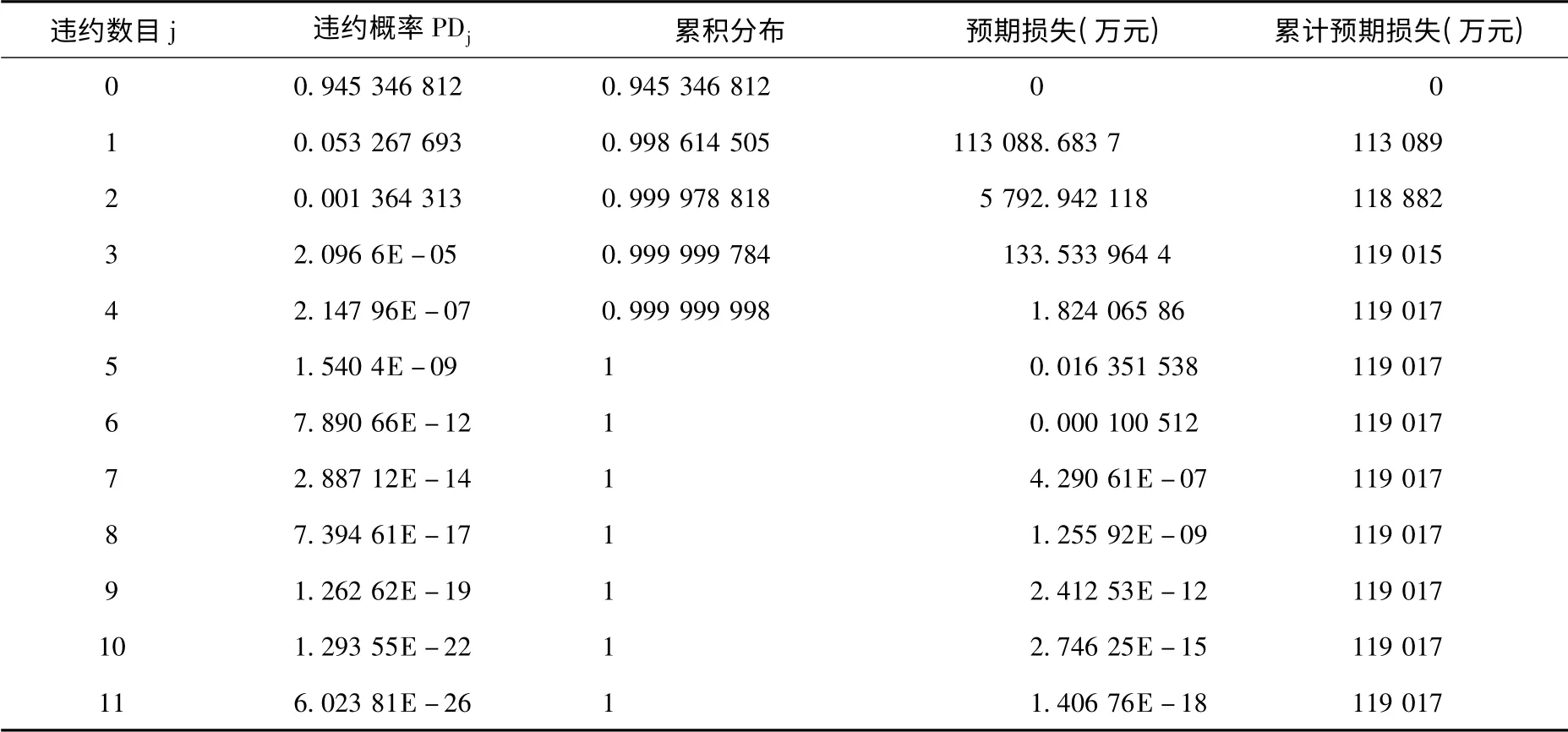
表3 北京银行理想资产池的违约损失情况(2013年)

5．经济资本的比较

按照巴塞尔协议对置信水平的规定，置信水平1－α 设为99.9%。根据ASRF 模型的计算公式(2)和二项式扩展技术的计算公式(9)，结合表2 和表3 中的违约分布情况，分别计算两家银行2008年至2013年的经济资本，两种模型计算结果如表4 和表5所示。

表4 2008－2013年宁波银行的经济资本

表5 2008－2013年北京银行的经济资本

结果表明，运用ASRF 模型计算的经济资本小于利用二项式扩展技术得出的经济资本，这正是因为城市商业银行信贷投放的行业集中度比较明显，而ASRF 模型并没有考虑这部分风险，故低估了银行所需的经济资本。此外，表4 和表5 中北京银行和宁波银行历年的贷款损失准备小于相应年份银行所需的经济资本，说明银行的损失准备不足以应付面临的风险，一旦发生贷款违约，银行可能会陷入困境。

四、结论

信贷集中风险与经济资本的计量和管理是一个值得深入研究的课题。由于国内城市商业银行的经济资本管理整体水平不高，并且银行普遍存在披露数据质量不高的问题，因此信贷集中风险和经济资本的计量仍是商业银行信贷风险资本管理中的一大难点。

本文结合新《巴塞尔协议》中的渐进单因子模型，重点介绍考虑行业集中风险因素的二项式扩展技术，运用这两种方法分别对2008年至2013年间宁波银行和北京银行的经济资本进行测算。结果表明基于ASRF 模型计算的经济资本低于基于二项扩展技术计算的经济资本，说明行业集中风险的存在使商业银行需要更多的经济资本来抵御可能的信用风险;而且，银行计提的贷款损失准备不能抵御银行潜在的风险。

我国城市商业银行应该加快完善其公司治理机制，建立健全信用风险管理体系，加强经济资本管理理念和人才的培养，实施以风险集中为基础的经济资本管理，提高其抗风险的能力。

［1］褚应前，秦海坤．对县域经济信贷集中的思考［J］．金融纵横，2002(10):29－30．

［2］赵宇翔．基于违约率的银行信贷风险集中度研究［J］．金融发展研究，2008(6):30－33．

［3］Basel Committee on Banking Supervision．International Convergence of Capital Measurement and Capital Standards:A Revised Framework［J/OL］．2004－05－31］．www．bis．org．

［4］Gordy．A Risk－Factor Model Foundation for Ratings－Based Bank Capital Rules［J］．Journal of Financial Intermediation，2003(12):199－232．

［5］Pykhtin．Multi－factor Adjustment［J］．Risk，2004(8):85－90．

［6］Cespedes．A Simple Multi－Factor“Factor Adjustment”for the Treatment of Diversification in Credit Capital Rules［C］．Basel:BIS press，2006．

［7］姚奕，杜音颖．解读巴塞尔新资本协议资本计提的原则和方法［J］．新金融，2007(3):33－37．

［8］杨继光，刘海龙．商业银行组合信用风险经济资本测度方法研究［J］．金融研究，2009(4):143－158．

［9］秦学志，魏强，胡友群．信贷组合集中度风险计量模型综述［J］．现代管理科学，2012(1):23－24．

［10］Li Shujin，Lv Quan．Study on credit concentration of city commercial bank in ZheJiang province［J］．Proceeding of 2013 International Conference－WTO ＆Financial Engineering，2013(9):307－313．

［11］李红侠．商业银行贷款集中度风险的计量模型与实证研究［J］．海南金融，2010(2):25－29．

［12］Dullmann．Estimating asset correlations from stock prices or default rates –which method is superior?［J］．Banking and Financial Studies，2008(4):47－87．

［13］蒋建芳．浅析商业银行经济资本管理［J］．当代经济，2007(7):74－75．