不同船型干散货运价联动

李新伟, 余思勤, 陈金海(上海海事大学 .经济管理学院； .上海高级国际航运学院， 上海 201306)

不同船型干散货运价联动

李新伟a, 余思勤b, 陈金海a
(上海海事大学 a.经济管理学院； b.上海高级国际航运学院， 上海 201306)

为研究海岬型船、巴拿马型船、超灵便型船和灵便型船国际干散货运价的联动关系，建立自回归分布滞后(Autoregressivessive Distributed Lag,ADL)模型和动态条件相关系数多元随机波动率(DCC-MSV)模型，分别分析运价的领先滞后关系和风险传导过程。采用2009—2014年的数据做实证分析发现：海岬型船运价引导巴拿马型船运价，巴拿马型船运价引导灵便型船和超灵便型船运价，灵便型船运价和超灵便型船运价间存在较强的相互引导关系；海岬型船向巴拿马型船溢出运价波动风险，超灵便型和灵便型船相互溢出运价波动风险。

交通运输经济学;干散货运价；ADL模型；DCC-MSV模型；波动溢出效应

干散货航运市场包括海岬型船、巴拿马型船、超灵便型船和灵便型船等4个子市场,其中海岬型船航运市场因规模大、运价高、波动性强，成为市场的主导。分析4个市场运价间的领先滞后关系和风险传导过程，有利于理解运价变化、判断未来走势。

对国际干散货航运市场的研究主要从船型、航线和租船方式等3个维度，采用协整检验、Granger因果检验误差修正模型(Vector Error Correction Model,VECM)等分析运价的领先滞后关系，采用MGARCH(Multivariate Generalized AutoRegressive Conditional Heteroskedasticity)和MSV(Multivariate Stochastiic Volatility)等模型分析风险传导过程。ZHANG等[1]采用VECM模型分析即期与远期、程租与期租市场运价间的引导关系；朱意秋等[2]采用EGARCH模型分析国际干散货运输C3和C5航线即期与远期运费间的波动溢出效应；CHEN等[3]采用协整检验、Granger因果检验和ECM-GARCH模型分析不同航线上海岬型船及巴拿马型船运价的动态关系和波动溢出效应；范永辉等[4]采用三元BEKK-GARCH模型分析海岬型船、巴拿马型船和灵便型船运价间的波动溢出效应，发现海岬型船对巴拿马型船与灵便型船单向溢出，巴拿马型船和灵便型船之间双向溢出。随着更具灵活性和适用性的MSV模型不断完善[5]以及基于MCMC参数估计方法逐渐成熟，MSV模型被引入航运领域。宫晓婞[6]采用MSV模型研究巴拿马型船FFA市场及其他FFA市场的波动溢出效应；宋旭变[7]采用EGARCH和VS-MSV模型研究干散货FFA中C5和P3A航线即期运价与远期运价的波动溢出效应。此外，文献[8]和文献[9]还对干散货运价与集装箱运价的领先滞后关系和波动溢出效应、新造船运价与二手干散货船价格间的波动溢出效应等内容进行研究。

由以上研究可知，对国际干散货运价引导关系和波动溢出效应的研究注重影响方向，不注重影响的滞后期和强度,也较少采用MSV模型。对此,采用自回归分布滞后(Autoregressivessive Distributed Lag,ADL)模型和DCC-MSV模型，从方向、时滞和强度等3个角度分析4种干散货船型运价的领先滞后关系和风险传导过程，以便及时把握和规避风险，为船舶所有人、航运公司及货主等企业或相关人员的经营决策提供参考，促进国际干散货运费衍生品。

1 数据准备

1.1数据选取

国际干散货运价以海岬型船运价指数(Baltic Capesize Index,BCI)、巴拿马型船运价指数(Baltic Panamax Index,BPI)、超灵便型船运价指数(Baltic Supramax Index,BSI)及灵便型船运价指数(Baltic exchange Handy Size Index,BHSI)为代表。这里采用改变计算规则后的2009年7月1日至2014年12月24日的波罗的海干散货指数(Baltic Dry Index,BDI)做实证分析。

图1为4种船型的BDI，数据来源于Clarkson数据库。从图中可看出：船型越大，运价指数越高，波动性越强，且变动具有一定的领先性。

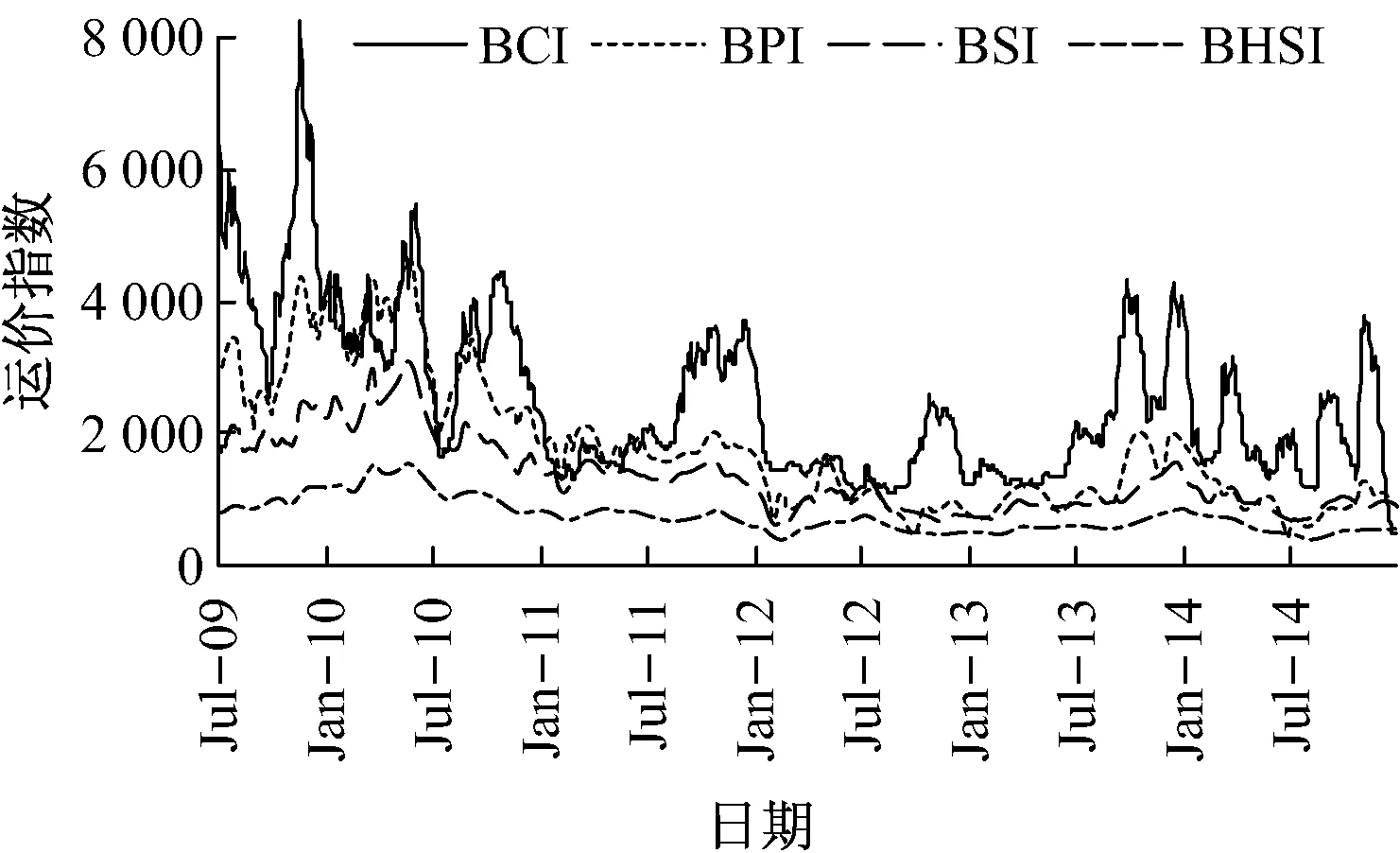
图1 4种船型的BDI

1.2数据处理

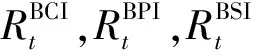
表和的基本统计特征

2 运价的领先滞后关系

若各船型的运价不仅受自身滞后期的影响，而且受其他船型运价滞后期的影响，则可建立ADL模型模拟运价变化。ADL模型可表示为

(1)

(2)

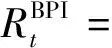
(3)

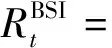
(4)

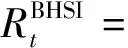
(5)

参数估计结果显示，各船型运价主要受自身滞后项和当期其他船型运价的影响。

1) 在方向上:海岬型船运价和巴拿马型船运价互为滞后相关，前者对后者的影响滞后期更长，说明BCI领先于BPI波动；超灵便型船运价和灵便型船运价互为滞后相关，且滞后期基本相当，说明HSI和BHSI的波动相互引导。此外，BPI引导BSI和BHSI波动，其他船型运价之间不存在相互引导关系。

2) 在滞后期上:BCI对BPI,BSI对BHSI,BHSI对BSI引导的滞后期均为3;BPI对BCI,BPI对BHSI引导的滞后期均为1，说明领先时间较短。

3) 在强度上:BHSI对BSI的引导强度最大，BSI对BHSI的引导强度次之，BCI对BPI的引导强度较小，BPI对BCI的引导强度为负。

因此,灵便型船运价与超灵便型船运价间存在较强的相互影响关系，海岬型船运价引导巴拿马型船运价波动，巴拿马型船运价引导灵便型船和超灵便型船运价波动，其他船型运价之间不存在明显的引导关系，据此可更加准确地预测运价走势。

3 运价的风险传导过程

3.1DCC-MSV模型

多元SV模型适合研究不同资产、不同行业间的相关性和风险溢出效应，其波动由滞后期波动率和不可测的随机过程共同决定。从模型结构和实证分析看，SV类2个随机扰动项的设计比ARCH族模型更符合实际波动率要求。DCC-MSV模型适合研究动态相关关系和波动溢出效应，已在金融市场有所运用。[10-11]这里建立一般化的二元DCC-MSV模型

(6)

3.2模型参数估计

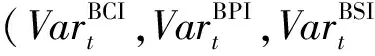
表和波动溢出效应参数

表2和表3中:MC误差远小于标准误差，说明参数估计结果收敛；各参数的边缘后验分布和密度估计曲线平滑，说明参数贝叶斯估计值误差非常小。

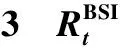
表和波动溢出效应参数

3.3波动溢出效应分析

对于运价波动风险评估，海岬型船只能根据自身的历史波动性进行推断，巴拿马型船可同时参考自身的和海岬型船的历史波动性，超灵便型船和灵便型船可参考自身的和对方的历史波动性，进行行业风险分析。船舶所有人、航运企业和货主可根据以上分析结果预判未来的运价波动风险。

4 结束语

为研究海岬型船、巴拿马型船、超灵便型船和灵便型船国际干散货运价的联动关系，分别建立ADL模型和DCC-MSV模型分析运价的领先滞后关系和风险传导过程。采用2009—2014年的BCI，BPI，BSI和BHSI数据进行实证分析。结果表明：在运价的领先滞后关系方面，海岬型船运价引导巴拿马型船运价波动，巴拿马型船运价引导灵便型船和超灵便型船运价波动，灵便型船运价与超灵便型船运价间存在较强的相互影响关系，其他船型运价之间不存在明显的引导关系；在运价的波动溢出效应方面，海岬型船向巴拿马型船溢出运价波动风险，超灵便型船和灵便型船相互溢出运价波动风险，其他船型之间不存在风险溢出效应。船舶所有人、航运企业和货主可根据不同船型国际干散货运价的领先滞后关系与风险传导过程，及时预判未来的运价变化，趋势防范运价波动风险。

[1] ZHANG J, ZENG Q, ZHAO X. Forecasting Spot Freight Rates Based on Forward Freight Agreement and Time Charter Contract[J]. Applied Economics, 2014, 46(29): 3639-3648.

[2] 朱意秋, 陈先洋. C3和C5航线远期运费波动溢出效应实证研究[J].中国海洋大学学报: 社会科学版, 2011(3): 28-32.

[3] CHEN S, MEERSMAN H, VANDE V E. Dynamic Interrelationships in Returns and Volatilities Between Capesize and Panamax Markets[J]. Maritime Economics & Logistics, 2010, 12(1): 65-90.

[4] 范永辉, 杨华龙, 刘金霞. 基于BEKK方差模型的干散货航运市场间波动溢出效应分析[J]. 数学的实践与认识, 2013, 42(23): 18-24.

[5] YU J, MEYER R. Multivariate Stochastic Volatility Models: Bayesian Estimation and Model Comparison[J]. Econometric Reviews, 2006, 25(2-3): 361-384.

[6] 宫晓婞. 干散货远期运费市场波动性及行为特征研究[D]. 大连:大连海事大学, 2011.

[7] 宋旭变. 干散货航运FFA市场波动溢出效应研究[D]. 大连:大连海事大学, 2012.

[8] HSIAO Y J, CHOU H C, WU C C. Return Lead-Lag and Volatility Transmission in Shipping Freight Markets[J]. Maritime Policy & Management, 2013(Ahead-of-Print): 1-18.

[9] DAI L, HU H, CHEN F,etal. Volatility Transmission in the Dry Bulk Newbuilding and Secondhand Markets: An Empirical Research[J]. Transportation Letters, 2014, 6(2): 57-66.

[10] KU Y C, BLOOMFIELD P, GHOSH S K. A Flexible Observed Factor Model with Separate Dynamics for the Factor Volatilities and Their Correlation Matrix[J]. Statistical Modelling, 2014, 14(1): 1-20.

[11] ACHCAR J A, CEPEDA C E, BAROSSI F M. Multivariate Volatility Models: An Application to IBOVESPA and Dow Jones Industrial[J]. Cuadernos de Economía, 2012, 31(56): 301-320.

[12] 杨华龙,刘金霞,范永辉.波罗的海干散货运价指数波动性研究[J].中国航海，2011,34(3): 84-88.

Lead-LagandVolatilitySpilloverAmongDryBulkShippingFreights

LIXinweia，YUSiqinb，CHENJinhaia
(a. School of Economics & Management; b. Shanghai Advanced Institute of International Shipping, Shanghai Maritime University, Shanghai 201306, China)

The Autoregressive Distributed Lag (ADL) model and the Dynamic Conditional Correlation Multivariate Stochastic Volatility (DCC-MSV) model are respectively adopted to detect the Lead-lag correlation of return and volatility spillover effect among international dry bulk shipping markets. The empirical results suggest that the return of BCI lead BPI, which lead both BSI and BHSI, while the return of BSI and BHSI lead each other. The Volatility Spillover from BCI to BPI, while that of BSI and BHSI Spillover to each other.

traffic transport economics; dry bulk shipping freight； ADL model； DCC-MSV model； volatility spillover effect

2015-07-11

教育部高等学校博士学科点专项科研基金(20113121110003)

李新伟(1975—)，女，山东青岛人，副教授，博士生，从事交通运输规划与管理研究。E-mail：lxw@163.com

陈金海(1986—)，男，浙江台州人，博士生，从事交通运输经济与管理研究。E-mail：jinhaichen2005@163.com

1000-4653(2015)03-0131-04

F224，F551

A