倾斜河岸水域沿岸斜航船舶水动力数值计算

张 科, 邹早建, b(上海交通大学 . 船舶海洋与建筑工程学院； b. 海洋工程国家重点实验室， 上海 200240)

倾斜河岸水域沿岸斜航船舶水动力数值计算

张 科a, 邹早建a, b
(上海交通大学 a. 船舶海洋与建筑工程学院； b. 海洋工程国家重点实验室， 上海 200240)

以集装箱船KCS船模为研究对象，采用基于雷诺平均纳维尔-斯托克斯方程求解的计算流体动力学(Computational Fluid Dynamics, CFD)方法，对在倾斜河岸水域沿岸匀速斜航船舶的黏性流场进行数值模拟并计算船体水动力，计算中基于低速假设忽略自由面兴波的影响。通过对不同水深和河岸倾角进行计算，分析这些因素对船舶所受水动力的影响，得到船舶所受横向力或转艏力矩为0时的漂角。该研究可为船舶在相关限制水域进行操纵与控制提供指导，以保证其安全航行。

水路运输； 倾斜河岸； 斜航； 水动力； 计算流体动力学； 数值计算

近岸航行的船舶通常会因岸壁效应的影响而受到一个岸吸力和一个艏推力矩的作用[1]，若不操舵加以控制，可能会以某一漂角作斜航运动而无法维持直航状态。与在无限水域直航相比，船舶在浅水航道等限制水域沿岸斜航时的绕流场更加复杂，所受水动力和操纵性能也与无限水域有很大不同。因此，研究船舶在浅水航道沿岸航行时的水动力性能，对于指导船舶驾驶员正确操控船舶，避免碰撞、触底等事故发生，保证船舶安全航行而言，具有重要的现实意义。

在过去几十年中，相关学者对船舶在限制水域中的操纵水动力进行的大量模型试验、理论与数值计算研究，主要基于势流理论的细长体理论和三维面元法。HESS[2]针对船舶靠近垂直岸壁航行的情况提出了一套计算船舶所受横向力的理论模型。KING等[3]采用细长体理论方法对某一数学船型在倾斜河岸水域中航行时的水动力进行了数值计算，分析了河岸倾角和水深对船舶水动力的影响。HE等[4]采用细长体理论方法对某一实际船型在倾斜河岸水域中航行时的水动力进行了数值计算，分析了船-岸距离、水深及河岸倾角对船舶水动力的影响。熊新民等[5]采用三维Rankine源面元法计算了船舶近岸航行时的水动力。随着计算机技术飞速发展，计算流体动力学(Computational Fluid Dynamics, CFD)方法在船舶水动力学领域得到了广泛应用。目前已有学者采用CFD方法进行限制水域中船舶操纵水动力的计算研究。LO等[6]应用FLOW-3D软件计算了某集装箱船模近岸航行时受到的水动力。王化明[7]应用FLUENT软件对几种船型在浅水和浅窄航道中斜航、回转及近岸航行时的黏性流场进行数值模拟，计算了相关水动力。ZOU等[8-9]应用SHIPFLOW软件对浅水中近岸航行船舶的水动力及船体下蹲现象进行了研究;同时,应用不确定度分析方法对计算结果的可靠程度进行了考察。

尽管倾斜河岸水域是一种常见的限制水域，但相关的试验研究比较缺乏，理论与数值计算研究也很少。对此，采用基于雷诺平均纳维尔-斯托克斯方程求解的CFD方法，对其进行数值研究。以集装箱船KCS船模为研究对象，针对船舶在倾斜河岸水域沿岸匀速斜航时的情况，应用CFD商业软件FLUENT对船舶的黏性绕流场进行数值模拟，计算船舶所受的水动力。计算中考虑到船舶在限制水域中航行时航速较低的特点并基于已有的研究结果[10]，忽略自由面兴波的影响。通过对不同水深和不同河岸倾角工况进行计算，分析这些因素对船舶所受水动力的影响，确定船舶在倾斜河岸水域沿岸斜航时所受横向力或转艏力矩为0时的漂角。

1 控制方程

图1为研究所用坐标系，考虑船舶在倾斜河岸水域中以速度U沿河岸匀速斜航时的情况。采用2个右手直角坐标系，其中：oxy平面和o0x0y0平面位于无扰自由面上；z轴和z0轴垂直向上为正。α为漂角，定义艏部指向岸壁时α为正，背离岸壁时为负。

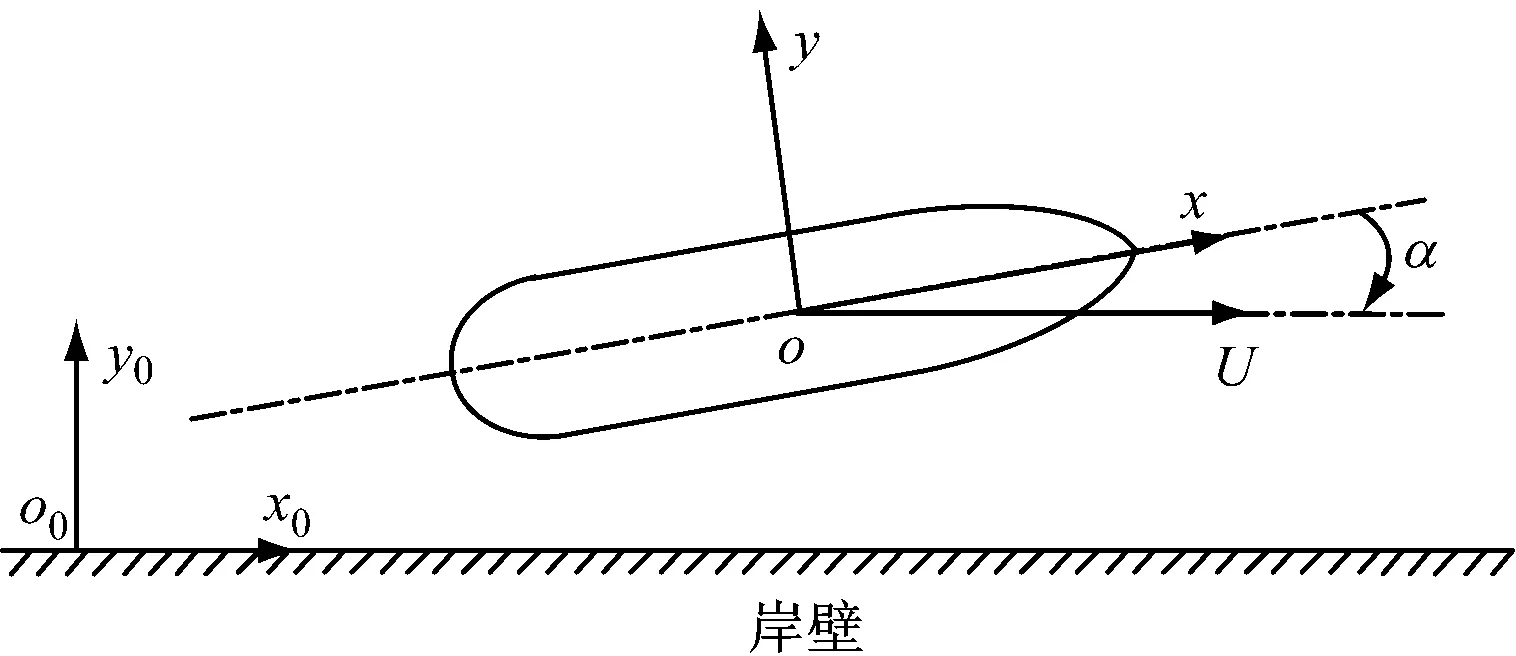
图1 坐标系

采用雷诺平均法，在空间固定坐标系下所考虑的黏性流体定常流动的控制方程为

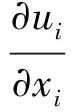
(1)

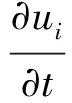
i,j=1,2,3

(2)

选择SSTk-ω两方程湍流模型来封闭控制方程组。[7]SSTk-ω湍流模型的湍流动能k和湍流耗散率ω方程为

(3)

(4)

式(3)～式(4)中：Γk和Γω为扩散系数；Gk和Gω为湍流生成项；Yk和Yω为湍流耗散项;Dω为横向扩散项。

2 数值求解

2.1计算对象

选取集装箱船KCS船模为计算对象，其缩尺比为36∶1。该船型是SIMMAN2008专题研讨会[11]组织国际比较研究的标准船型之一，其轮廓图见图2，实船船型参数见表1。

图2 KCS船型轮廓图

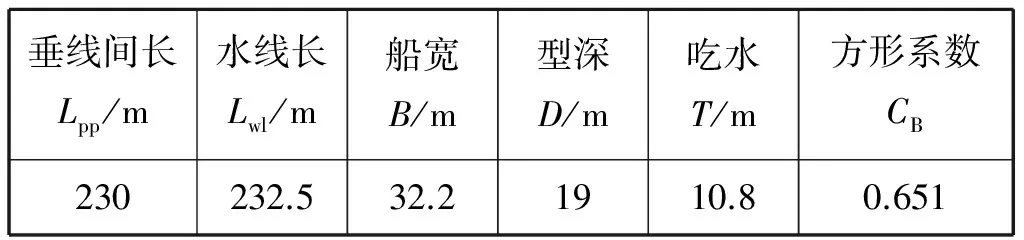
表1 KCS实船船型参数

2.2计算域及边界条件

研究船舶定常斜航运动情况，根据相对运动原理，假定船舶不动，水流以-U的速度流向船舶。计算域及其边界见图3，图中θ为河岸倾角。水深h定义为船舶中纵剖面与中横剖面交线在无扰自由面上的交点到水底的垂直距离。计算域边界上的边界条件设置如下。

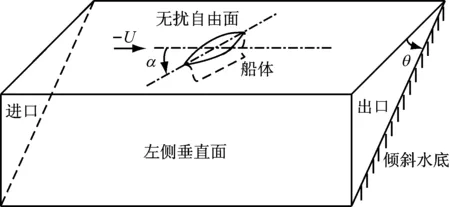
图3 计算域及其边界

1) 进口边界：距离艏部1.0Lpp，设定为速度入口(velocity-inlet)边界条件。

2) 出口边界：距离艉部3.0Lpp，设定为出口(outflow)边界条件。

3) 无扰自由面：假设船速很低，忽略自由面兴波的影响，在无扰自由面上设定为对称(symmetry)边界条件。

4) 倾斜水底：设定为移动壁面(wall)边界条件，移动速度为-U。

5) 船体表面：设定为无滑移壁面(wall)边界条件。

6) 左侧垂直面：距离船舶航行轨迹5.0B，在小漂角的假设下，其对船模周围流场的影响可忽略[1-7]，在其上设定为对称(symmetry)边界条件。

2.3数值方法

应用通用CFD软件FLUENT，采用分离式求解器进行上述黏性流体定常流动问题数值求解；由于流速低且流体不可压缩，压力项采用标准离散格式，其他项采用二阶迎风格式，以提高计算精度；压力-速度耦合方程采用SIMPLEC算法进行求解；亚松弛因子选择系统默认值。

3 计算结果及分析

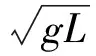
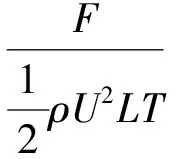
(5)

3.1水深的影响

在一定的河岸倾角下对不同水深、不同漂角进行计算，计算工况见表2。

表2 河岸倾角一定时的计算工况

计算结果见图4和图5，其中：图4为河岸倾角θ=10°时，不同水深下横向力系数和转艏力矩系数随漂角的变化关系；图5为河岸倾角θ=10°，水深吃水比h/T=2.0时不同漂角下无扰自由面和船体表面上的压力分布图。

从图4a中可看出：在一定的水深下，随着漂角由负变为正，横向力由正变为负，即当艏部由离岸转向靠岸时，船舶所受横向力由岸推力变为岸吸力，这可从图5中得到验证；此外，当船舶以某一负的漂角斜航时，其所受横向力为0，水深吃水比越小，横向力为0的漂角的绝对值就越大。从图4b中可看出：在一定的水深下，随着漂角由负变为正，转艏力矩由正变为负，即当艏部由离岸转向靠岸时，船舶所受转艏力矩由艏推力矩变为艏吸力矩，这可从图5中得到验证；此外，当船舶以某一正的漂角斜航时，其所受转艏力矩为0，水深吃水比越小，转艏力矩为0的漂角就越大。

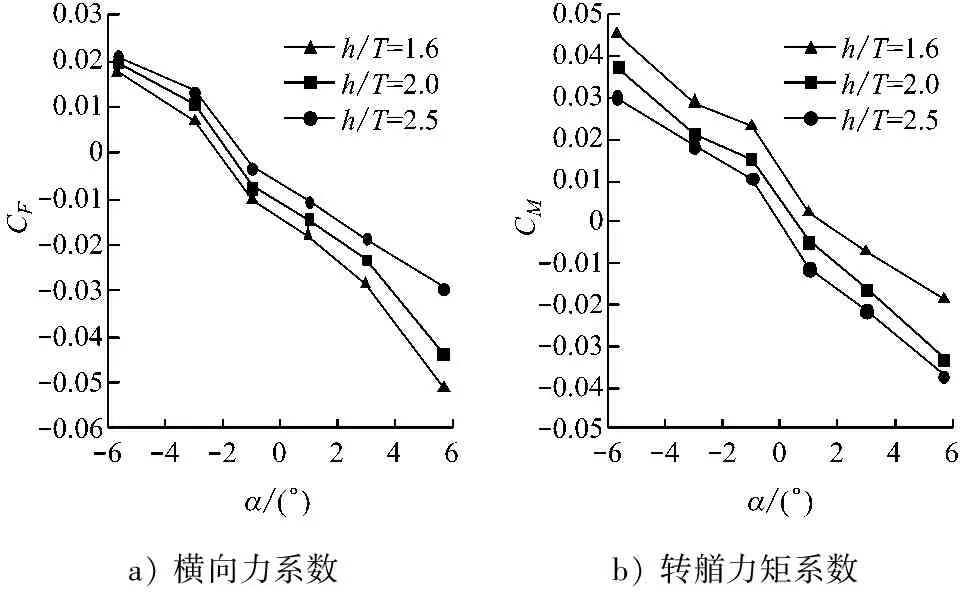
a)横向力系数b)转艏力矩系数

图4 不同水深下横向力系数和转艏力矩系数随漂角的变化关系(Fn=0.15,θ=10°)

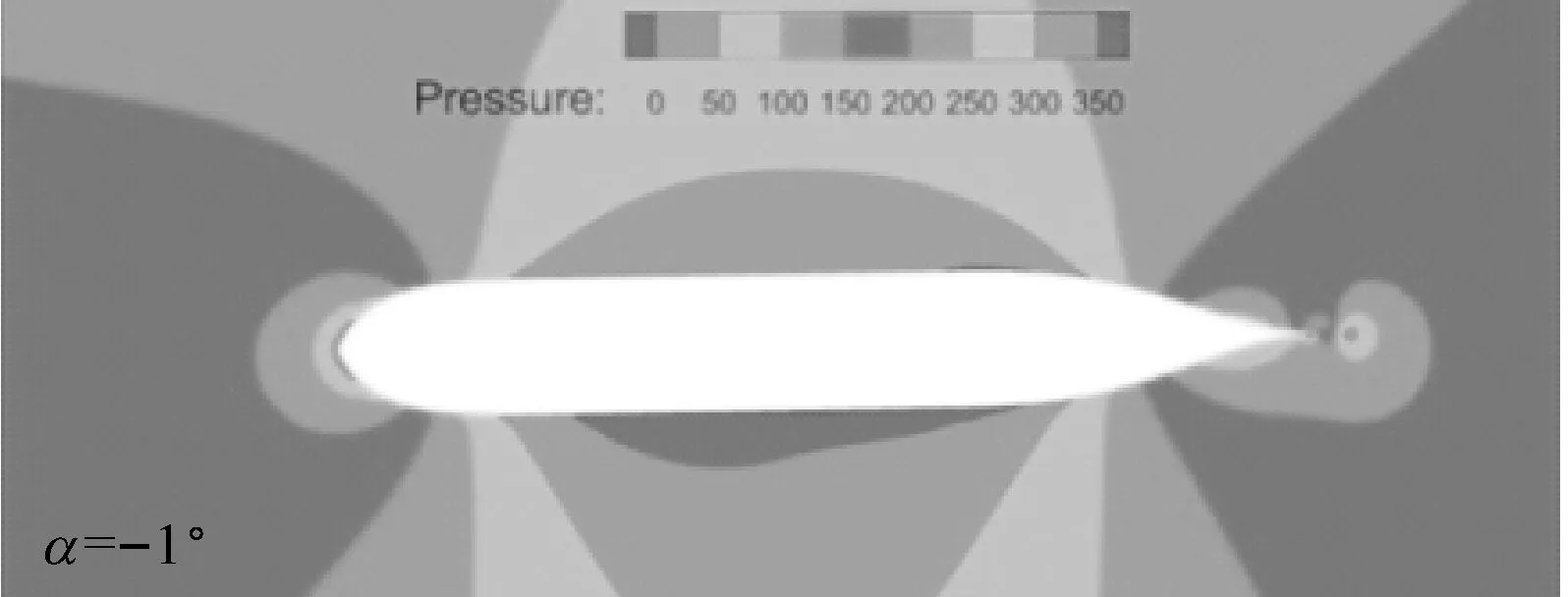
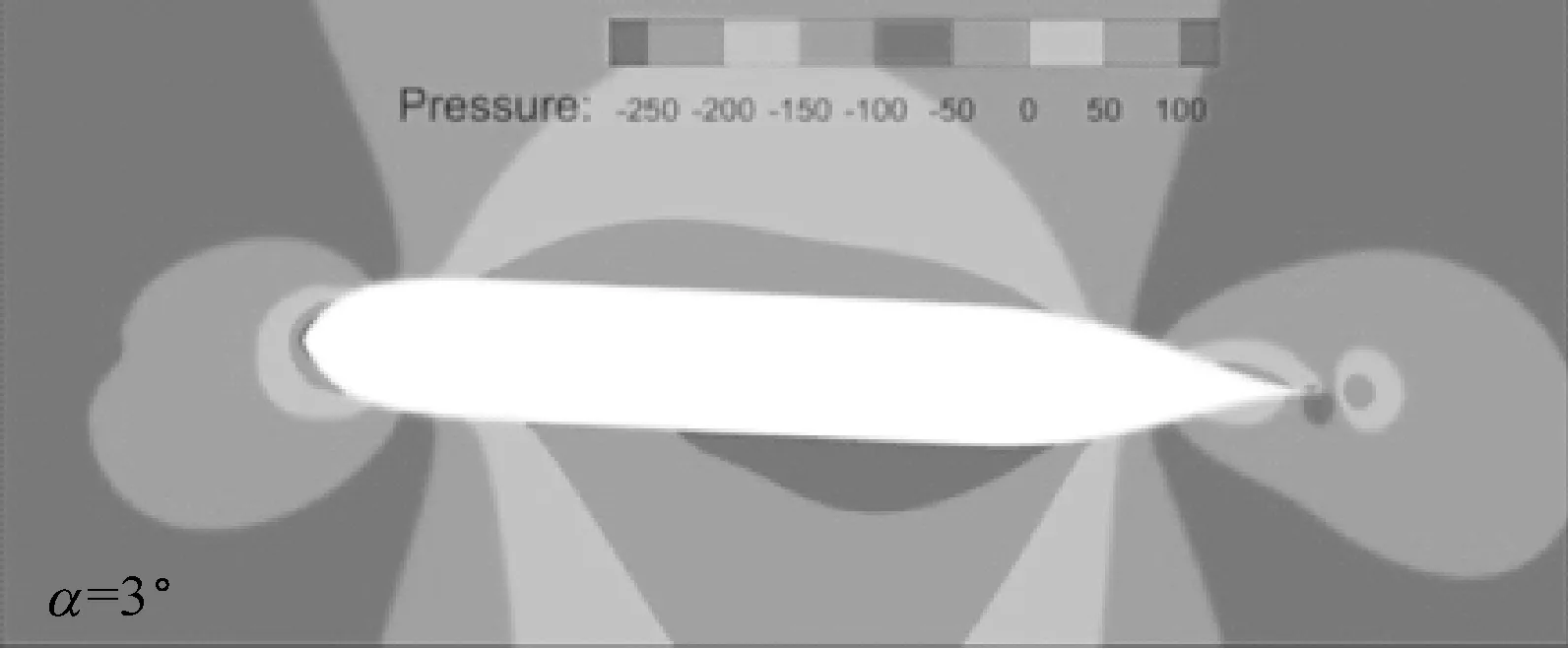
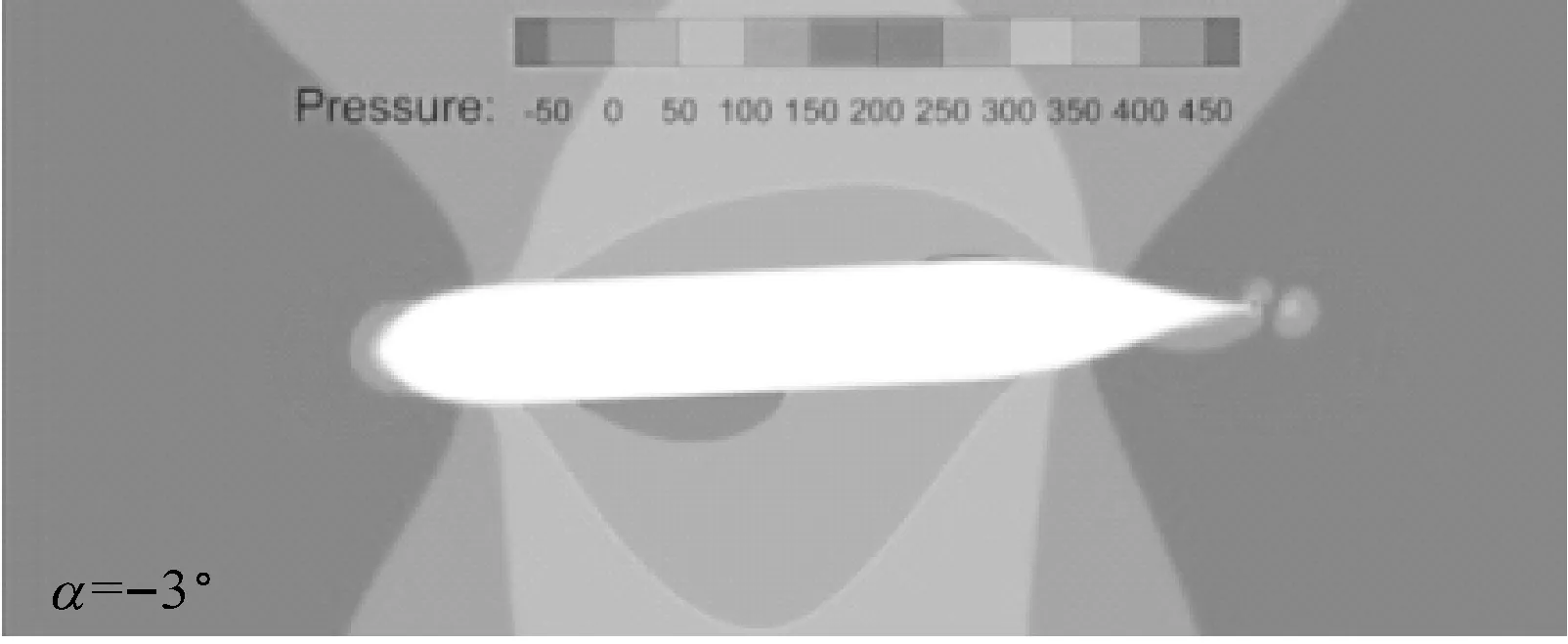
a) 无扰自由面压力图

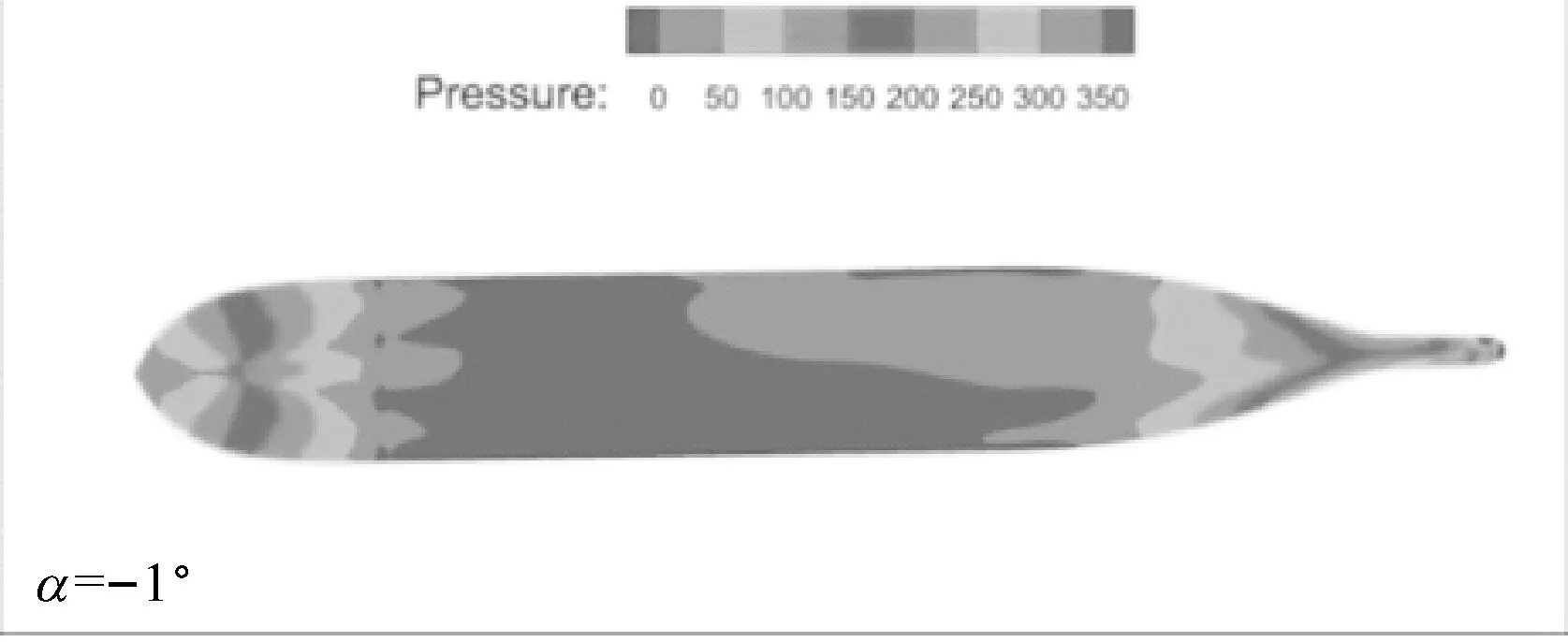
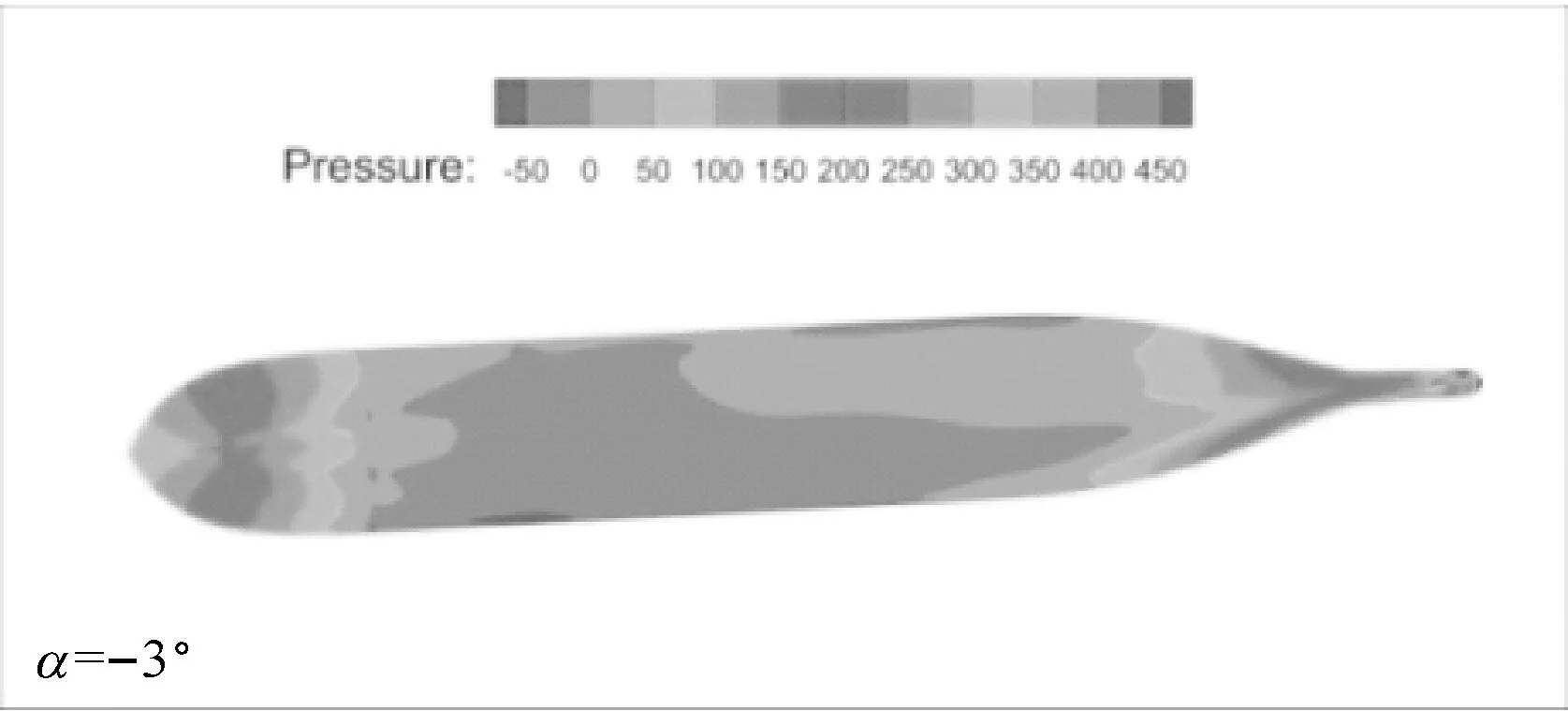
b) 船体表面压力图

图5 不同漂角下无扰自由面和船体表面上的压力分布图(Fn=0.15,h/T=2.0,θ=10°)

3.2河岸倾角的影响

在一定的水深下，对不同的河岸倾角、不同的漂角进行计算，计算工况见表3。

表3 水深一定时的计算工况

计算结果见图6和图7，其中：图6为水深吃水比h/T=2.0时，不同河岸倾角下横向力系数和转艏力矩系数随漂角的变化关系；图7为水深吃水比h/T=2.0,河岸倾角θ=15°时，不同漂角下无扰自由面和船体表面上的压力分布图。

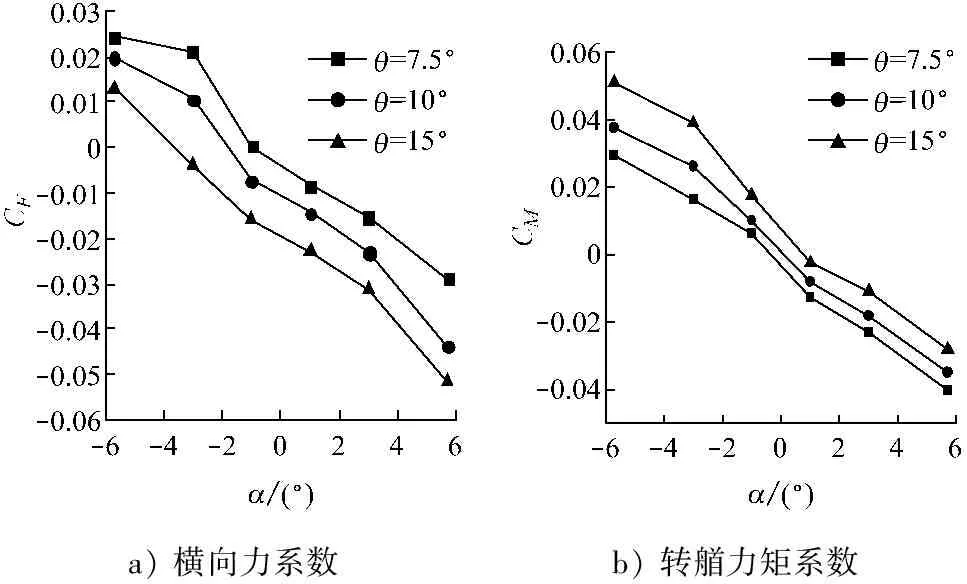
a)横向力系数b)转艏力矩系数

图6 不同河岸倾角下横向力系数和转艏力矩系数随漂角的变化关系(Fn=0.15,h/T=2.0)

从图6a中可看出：在一定的河岸倾角下，随着漂角由负变为正，横向力由正变为负，即当艏部由离岸转向靠岸时，船舶所受横向力由岸推力变为岸吸力，这可由图7验证；当船舶以某一负的漂角斜航时，其所受横向力为0，河岸倾角越小，横向力为0的漂角的绝对值就越小。从图6b中可看出：在一定的河岸倾角下，随着漂角由负变为正，转艏力矩由正变为负，即当艏部由离岸转向靠岸时，船舶所受转艏力矩由艏推力矩变为艏吸力矩，这可由图7验证；当船舶以某一正的漂角斜航时，其所受转艏力矩为0，河岸倾角越大，转艏力矩为0的漂角就越大。

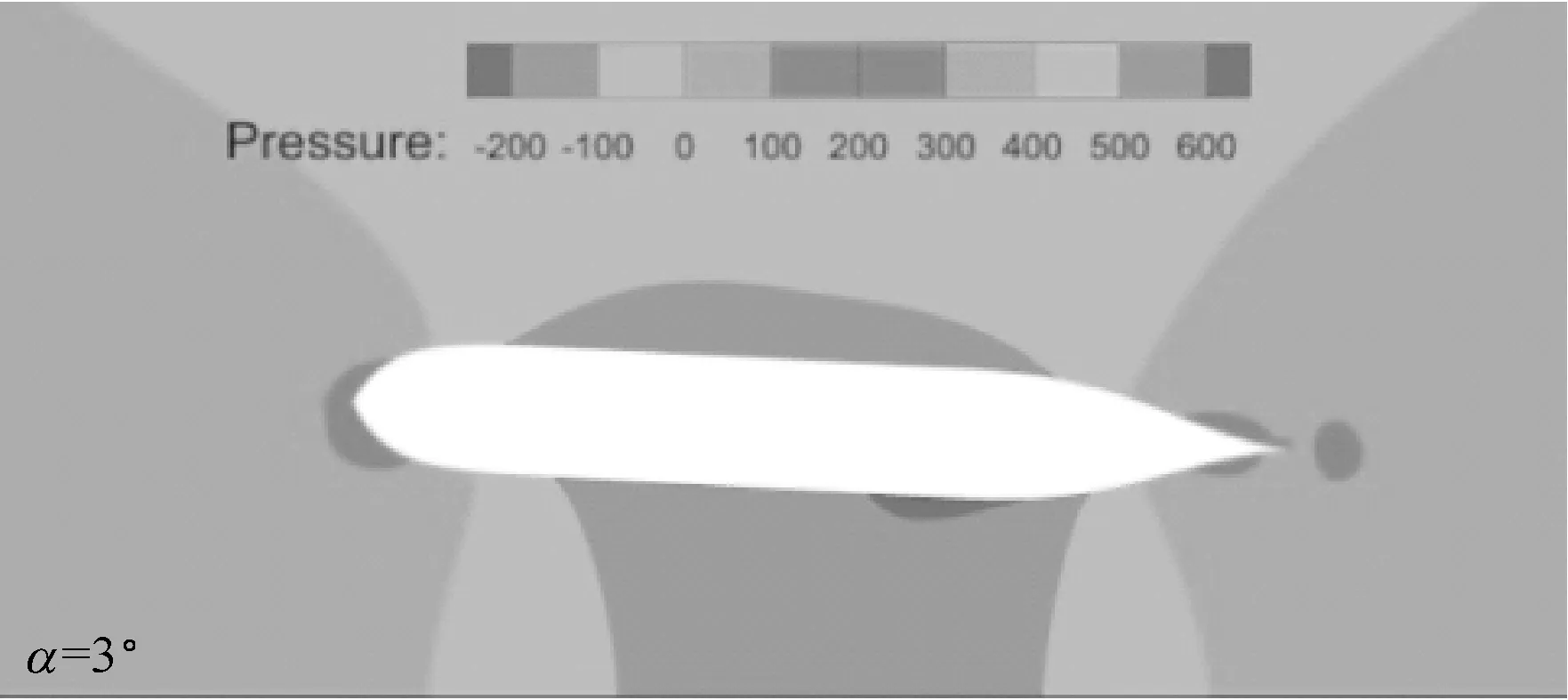
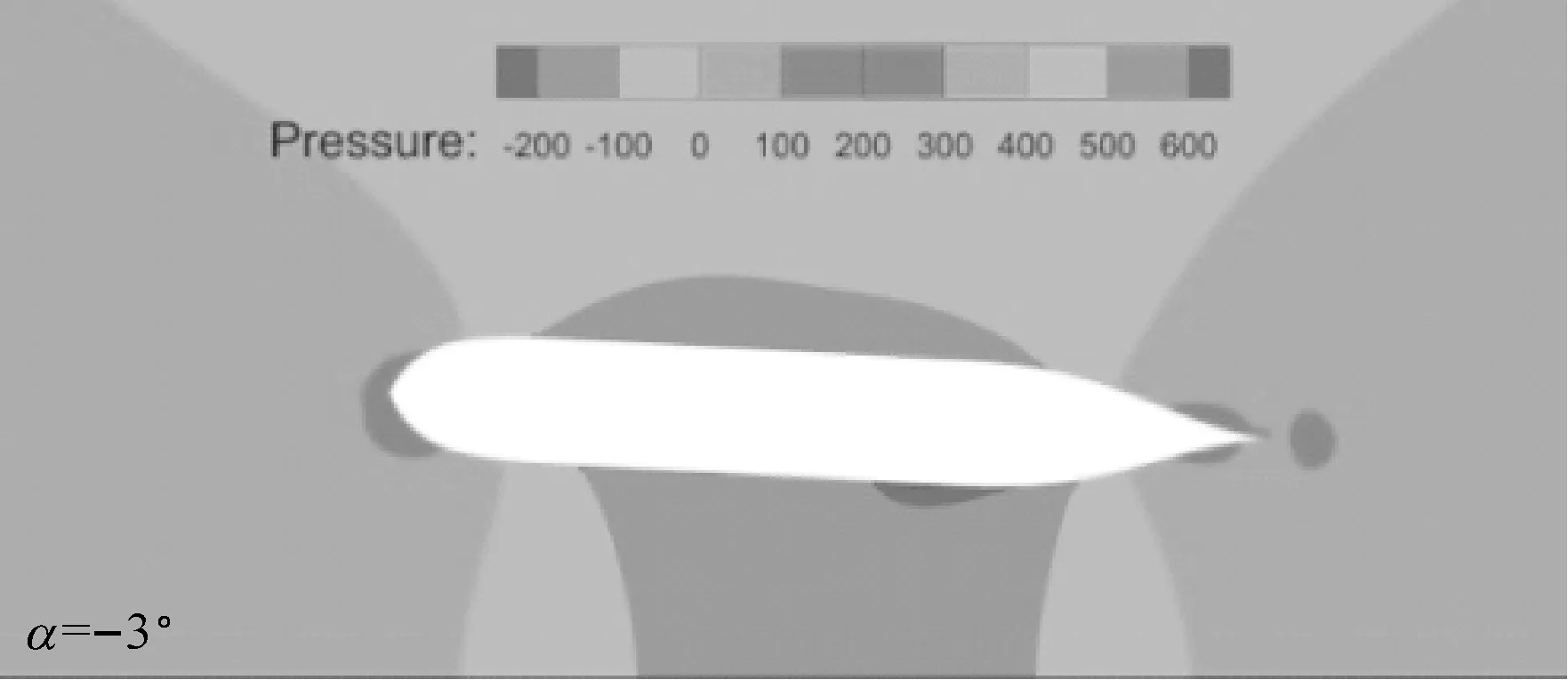
a) 无扰自由面压力图

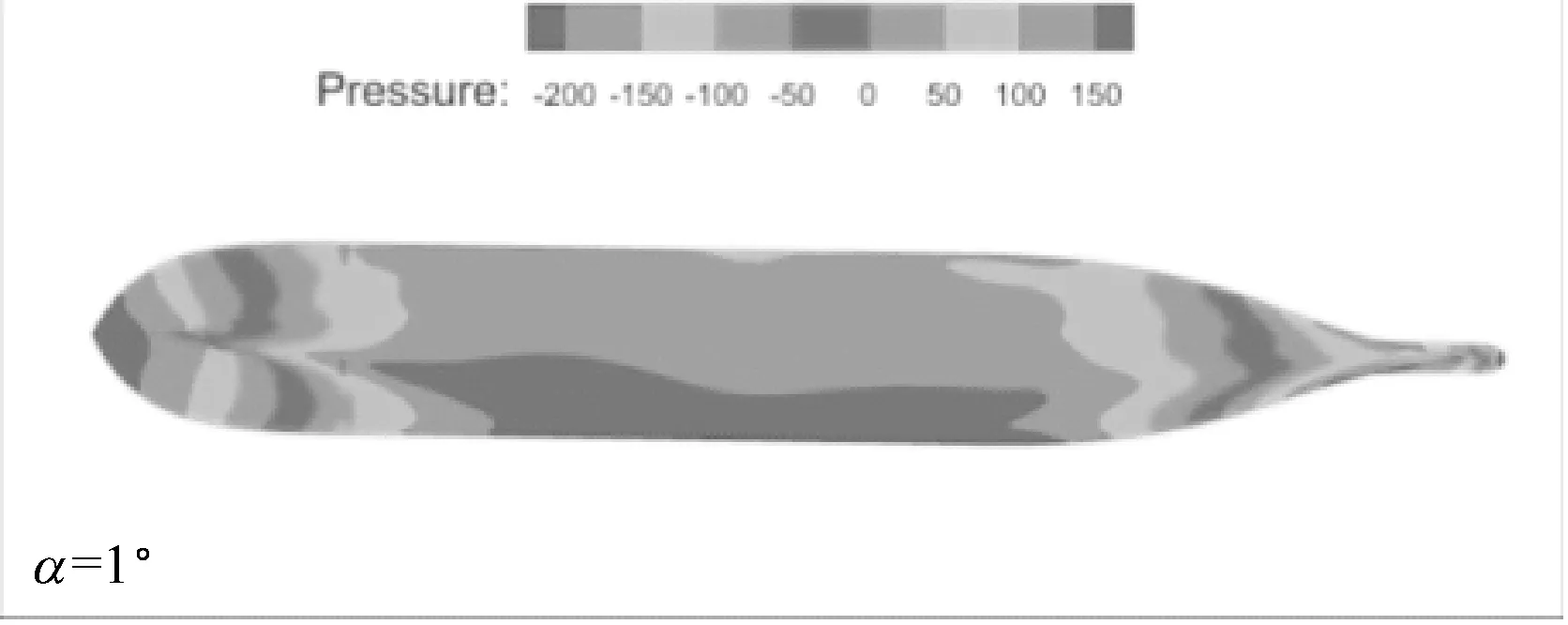
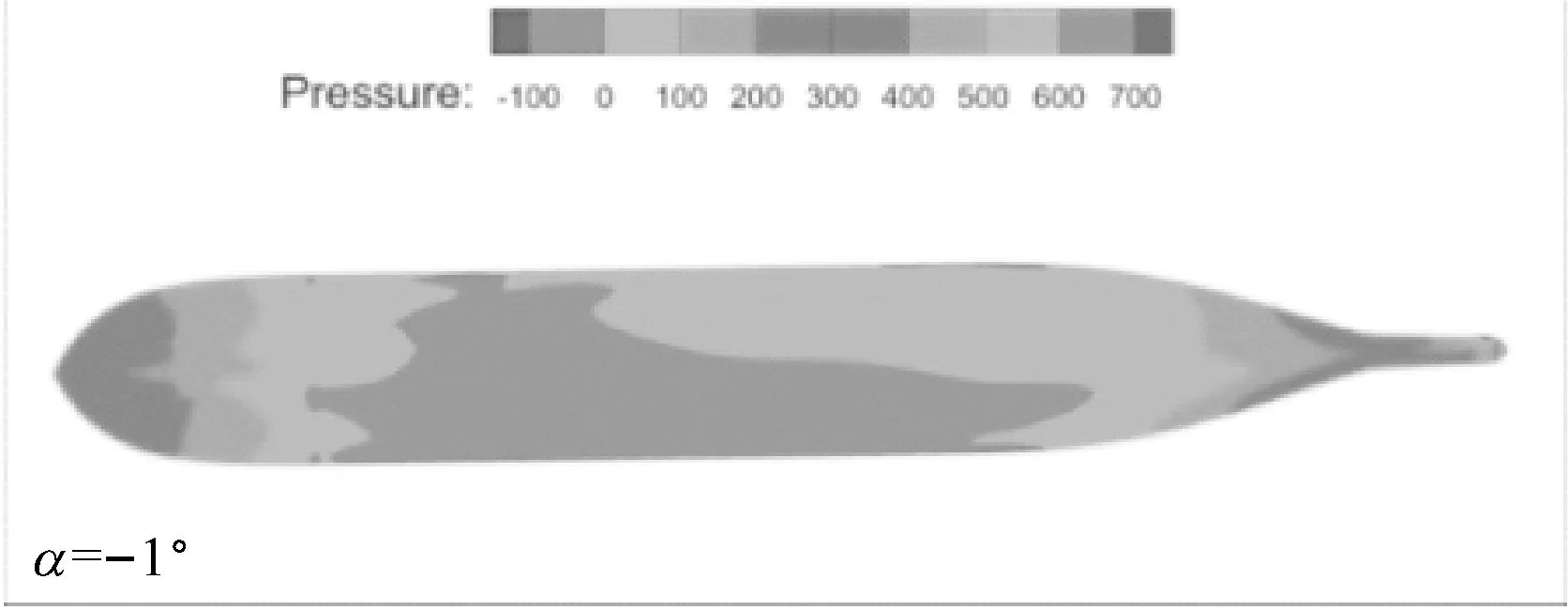
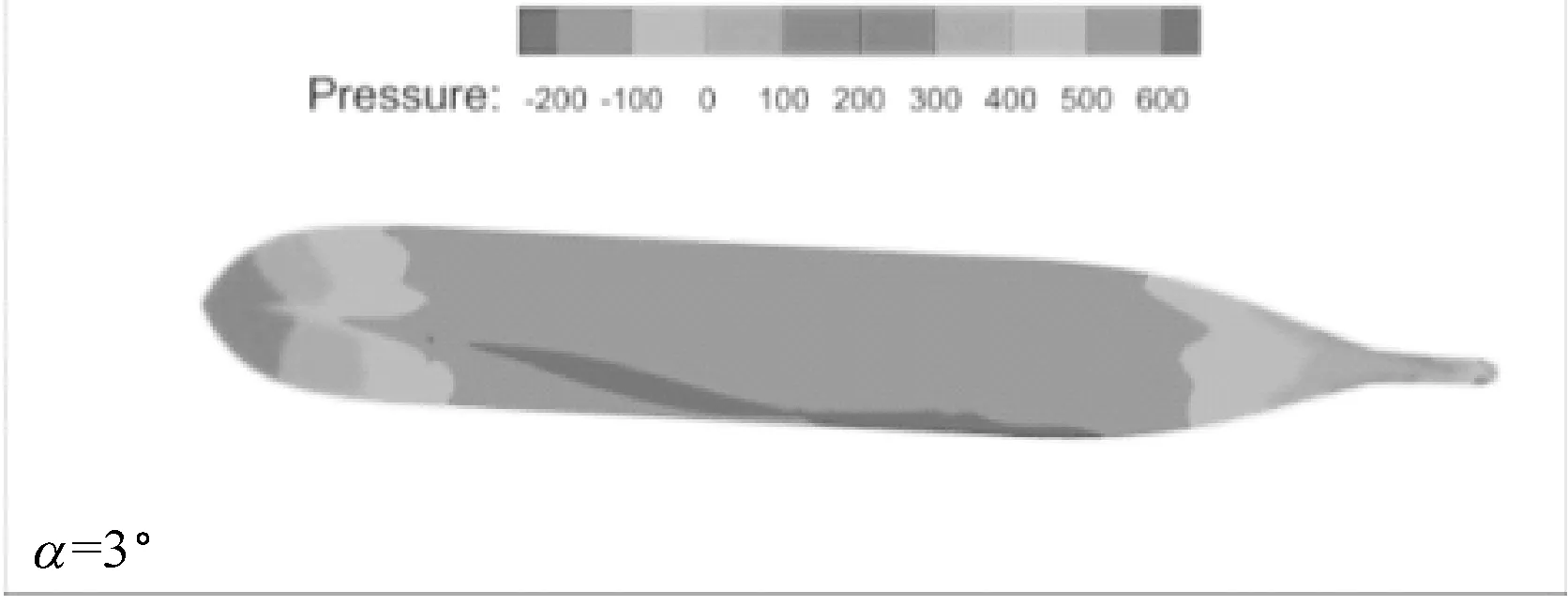
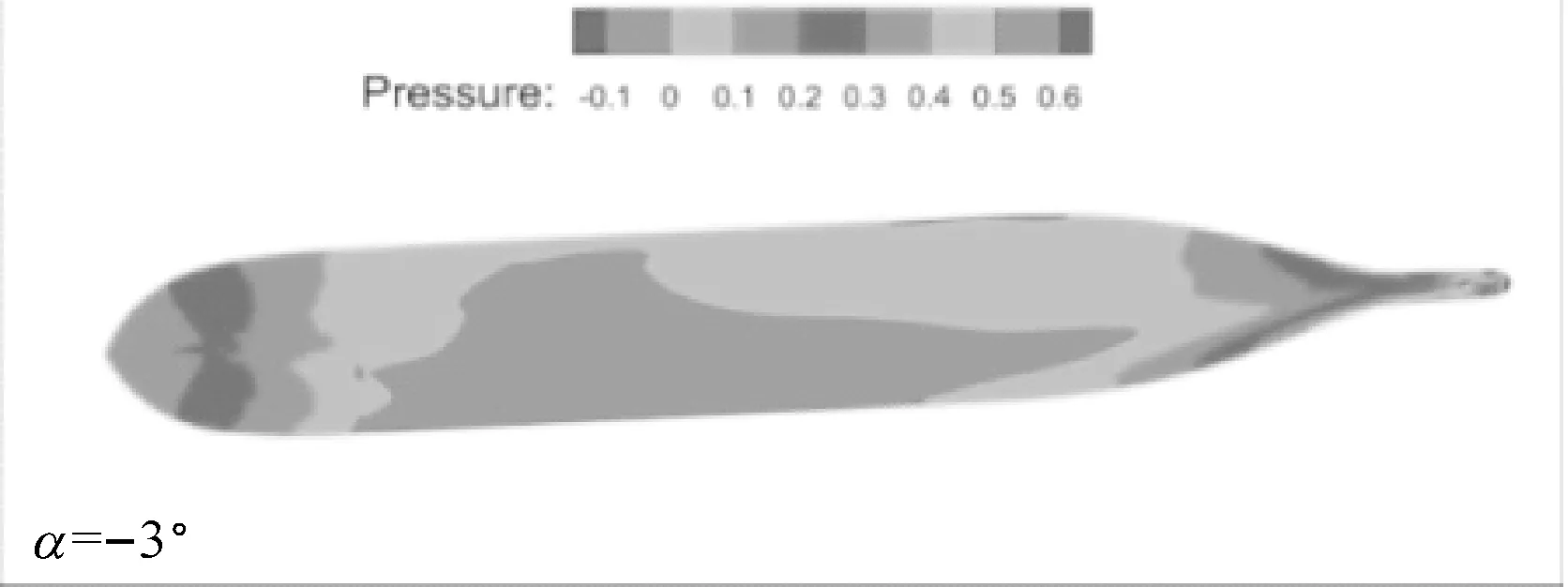
b) 船体表面压力图

图7 不同漂角下无扰自由面和船体表面上的压力分布图(Fn=0.15,h/T=2.0,θ=15°)

4 结束语

以集装箱船KCS船模为研究对象，应用CFD软件FLUENT对船舶在倾斜河岸水域沿岸斜航运动的黏性绕流场进行了数值模拟，计算得到了船舶所受横向力和转艏力矩；通过计算，分析了水深和河岸倾角对船舶所受水动力的影响，确定了船舶所受横向力或转艏力矩为0时的漂角。研究结果表明：在一定水深和一定河岸倾角下，随着漂角由负到正变化，船舶所受横向力和转艏力矩的作用方向均可能发生变化；当船舶以一定的漂角斜航时，其受到的横向力或转艏力矩为0。该研究结果可为船舶在相关限制水域进行安全操纵与控制提供一定的依据。但是，由于缺乏试验数据，水动力计算结果的精度有待进一步提高，这里所得到的结论仅仅是定性的，要得到定量的结论，还需作进一步的研究。

[1] 姚建喜. 船舶近岸航行岸壁效应数值研究[D]. 上海：上海交通大学, 2010.

[2] HESS F. Lateral Forces on a Ship Approaching a Vertical Wall: A Theoretical Model[J]. Journal of Ship Research, 1979, 23(4): 284-296.

[3] KING G F, TUCK E O. Lateral Forces on Ships in Steady Motion Parallel to Banks or Beaches[J]. Applied Ocean Research, 1979, 1(2): 89-98.

[4] HE Q, KIJIMA K. The Effect of Slope Bank on Hydrodynamic Forces Acting on a Ship[J]. Transactions of West-Japan Society of Naval Architects, 1989, 79: 53-60.

[5] 熊新民, 吴秀恒. 自由面和岸壁对限制航道中船舶操纵性水动力的影响[J]. 中国造船, 1994 (1): 34-44.

[6] LO D C, SU D T, CHEN J M. Application of Computational Fluid Dynamics Simulations to the Analysis of Bank Effects in Restricted Waters[J]. Journal of Navigation, 2009, 62(3): 477-491.

[7] 王化明. 限制水域操纵运动船舶黏性流场及水动力数值研究[D]. 上海：上海交通大学, 2009.

[8] ZOU L, LARSSON L, DELEFORTRIE G，etal. CFD Prediction and Validation of Ship-Bank Interaction in a Canal[C]. Proceedings of the International Conference on Ship Manoeuvring in Shallow and Confined Water: Ship to Ship Interaction, Trondheim, Norway, 2011.

[9] ZOU L, LARSSON L. Computational Fluid Dynamics (CFD) Prediction of Bank Effects Including Verification and Validation[J]. Journal of Marine Science and Technology, 2013, 18(3): 310-323.

[10] MA S J, ZOU Z J, HUANG L P. A Numerical Study on Bank-Effect Related Hydrodynamics[C]. 2ndInternational Conference on Maritime Technology and Engineering, MARTECH 2014, Lisbon, Portugal, 2014.

[11] SIMMAN 2008, Workshop on Verification and Validation of Ship Maneuvering Simulation Methods[DB/OL]. Copenhagen, Denmark, 2008. http://www.simman2008.dk.

NumericalCalculationofHydrodynamicForcesonShipSailingObliquelyAlongSlopingBank

ZHANGKea，ZOUZaojiana，b
(a. School of Naval Architecture, Ocean and Civil Engineering; b. State Key Laboratory of Ocean Engineering, Shanghai Jiao Tong University, Shanghai 200240, China)

With the model of KCS container ship as study object, the numerical simulation of the viscous flow around a ship sailing obliquely along a sloping bank with constant speed is conducted, and the hydrodynamic forces acting on the ship are calculated through solving the Reynolds-averaged Navier-Stokes equations by using the Computational Fluid Dynamics (CFD) method. Under the assumption of low ship speed, the effect of free surface elevation is neglected. With a series of computations for different water depth and sloping angle of the bank, the influences of these factors on the hydrodynamic forces are analyzed, and the drift angle at which the lateral force or yaw moment is zero is determined. The results of this study can provide a certain safety guidance on manoeuvring and control of ships sailing in such restricted waters.

waterway transportation; sloping bank; oblique motion; hydrodynamic forces; CFD; numerical calculation

2015-05-10

国家自然科学基金(51309152)

张科(1989—), 男, 湖南怀化人, 硕士, 从事限制水域船舶水动力数值研究。 E-mail: zhangkk14@sina.cn

邹早建(1956—), 男, 江西抚州人, 教授, 博士生导师, 从事船舶操纵与控制研究。 E-mail: zjzou@sjtu.edu.cn

1000-4653(2015)03-0052-05

U661.1

A