基于无模型的船舶航向跟踪控制
张玉喜(大连海事大学 航海学院,辽宁 大连 116026)
基于无模型的船舶航向跟踪控制
张玉喜
(大连海事大学 航海学院,辽宁 大连 116026)
针对非线性船舶航向运动数学模型中存在的显著不确定性问题及其控制器输入饱和限制问题,提出一种基于Backstepping的直接自适应神经网络控制方法。采用Backstepping方法对船舶航向控制系统进行递归式设计并借助一种饱和内补偿辅助系统处理系统中的输入饱和限制问题;同时,从实际应用的角度出发,充分考虑系统中存在的显著不确定性并运用径向基神经网络对不确定性进行估计和补偿,使所设计的控制器更贴近工程应用。仿真计算结果验证了所提控制方法在船舶航向控制系统中的有效性,可实现高精度的航向保持控制。
船舶工程;船舶航向控制;输入饱和;神经网络;后推
水路运输与人类文明的进步密切相关,是完成地区之间及国与国之间大宗货物贸易最有效、最经济的方式。然而,船舶在海上航行过程中会遇到各种各样的危险,且逐渐向着大型化、高速化和自动化方向发展,因此人们对船舶的操纵与控制性能提出了更高的要求。船舶运动控制技术的开发与研究必将受到越来越多的重视。
控制理论在船舶运动控制领域的应用较早,而控制策略是船舶运动控制科学的主要研究对象。为提高航向控制的精确度,并使其具有良好的鲁棒性,先后应用了多种先进的控制策略,如最小方差控制和线性二次高斯(Linear Quadratic Gaussian, LQG)控制等自适应控制策略[1]、广义预测控制[2]、变结构控制[3]和H∞鲁棒控制[4]等。此外,李俊方等[5-6]提出一种考虑输入饱和的基于神经网络的自适应跟踪控制算法,在其中引入了辅助系统以补偿饱和对系统造成的影响,最终使系统获得了良好的控制性和稳定性。总之,控制理论的发展为船舶运动控制系统的设计提供了诸多控制算法,为船舶运动科学的进一步发展注入了活力。
随着控制理论不断发展,基于Lyapunov函数的递归式设计思想(即Backstepping方法)在控制领域变得越来越流行,主要应用于具有不匹配特性的严格反馈下三角不确定非线性系统的控制设计中。但是,当系统的非线性数学模型呈现出高度的不确定性(例如不能被线性参数化、完全未知的不确定性)时,该方法的应用就会受到一定的限制。[7-8]因此,相关学者[9]进一步发展了各种基于模糊逻辑系统和神经网络等逼近器的自适应Backstepping控制方法。此外,从工程应用的角度出发,驱动器饱和限制作为一种重要的非光滑非线性项,经常出现在船舶的航向航迹控制系统中,且可能导致系统的控制性能变差,甚至破坏系统的稳定性。[10]对此,文献[11]针对具有输入饱和特性的海洋水面船舶进行了自适应神经网络跟踪控制,为消除输入饱和限制的影响引入了一种辅助设计系统。因此,为保障船舶航向控制系统的稳定性和控制性能,在控制设计中考虑系统的输入饱和问题是十分必要的。
综上,针对船舶航向运动非线性不确定数学模型,同时考虑系统的显著不确定性问题和执行器的饱和限制问题,将Backstepping技术与饱和内补偿辅助系统相结合,设计出一种自适应神经网络控制器,以解决系统输入饱和可能影响系统的控制性和稳定性的问题。此外,希望该研究工作可拓展船舶自动舵的选择范围,促使自动舵产品化,进而对船舶运动控制的发展产生一定的积极意义。
1 问题的描述与准备
1.1问题的描述
船舶航向非线性运动数学模型可描述为
(1)
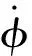
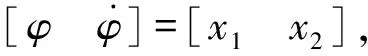
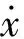
(2)
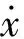
(3)
设计目标是在考虑系统的显著不确定性和输入饱和的情况下,针对船舶航向非线性运动控制系统,在Backstepping方法的基础上结合饱和辅助设计系统,设计一种鲁棒性好、适应性强、参数整定简单、控制精度较高的船舶航向控制器,保证船舶在恶劣环境中安全航行。
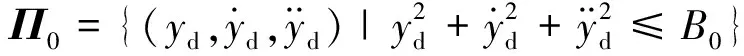
假设2g(·)是光滑的非线性未知函数,符号已知,存在g1>g0>0满足g1>|g(·)|>g0,存在常数gm>0使|g(·)|≤gm。即未知光滑函数g(·)是严格正的或负的,为不失一般性,假设g1>g(·)>g0。
1.2饱和内补偿系统
为处理系统的输入饱和问题,引进文献[10]295提到的辅助设计系统。考虑输入u的饱和限制为
-um≤u≤uM
(4)
式(4)中:-um和uM分别为已知输入u的最小值和最大值,即
(5)
式(5)中:v为整个系统要设计的控制输入。
1.3径向基函数神经网络(RBFNN)
在工程控制领域,径向基函数神经网络常被用于逼近有界的非线性函数,可表示为WTS(Z),其中:Z∈Ω⊂Rn为输入矢量;W∈Rl为权重;S(Z)∈RL为激活函数;L为节点数。万能逼近定理表示为:若节点数L选的足够大,则在某个紧致集上,WTS(Z)能使任意的连续函数逼近到理想的精度上。即
h(Z)=W*TS(Z)+ε
(6)
式(6)中:W*为理想常数权值;ε为逼近误差;S(Z)=[s1(Z),s2(Z),…,si(Z)]T,si(Z)经常选为高斯函数,其形式为
(7)
式(7)中:μi为中心值;ηi为高斯函数的宽度;1 针对非线性船舶航向运动数学模型中存在的显著不确定性问题及其控制器输入饱和限制问题,在Backstepping方法的基础上结合饱和辅助设计系统,设计一种鲁棒性好、控制精度高的船舶航向控制器,保证船舶在海上安全航行,下面为简要的设计过程。 步骤1定义跟踪误差z1=x1-yd并对其求导得 (8) 定义 z2=x2-a2 (9) 式(9)中:a2为虚拟控制律。 对式(9)做适当变换并将其代入式(8)得 (10) (11) 选择虚拟控制律 (12) 式(12)中:k1>0,为设计参数。 将式(12)代入式(11)得 (13) 为便于考虑系统输入饱和的影响,选取以下辅助设计系统。 (14) 式(14)中:k4>0,ε0>0,为设计参数;Δu=u-v;e是为减弱输入饱和对系统的影响而引进的变量;v为要设计的控制律。 步骤2对z2求导得 (15) 由式(6)可知 (16) 式(16)中:|ε|≤ε*且Z=[x1,x2]T。 将式(16)代入式(15)得 (17) 选取李雅普诺夫候选函数 (18) 对V2求导得 (19) 选择控制律v为 (20) 将式(20)代入式(19)得 (21) 注意到 (22) (23) (24) (25) (26) 选取自适应律 (27) 式(27)中:σ为小的设计参数。 注意到 (28) (29) 由式(29)可得 (30) 以大连海事大学远洋教学实习船“育鲲”轮为例进行仿真研究,以验证所提控制算法的有效性。该船的国际海事组织(International Maritime Organization, IMO)识别号为9378132,船长116 m,船宽18 m,设计吃水5.4 m,方形系数0.56,排水量5 735.5 t,舵面积11.8 m2。通过计算可得船舶非线性运动数学模型参数K=0.31,T=62.38。 选择跟踪信号时,选取能代表某一实际性能要求的数学模型,即 0.002 5φr(t) (31) 式(31)中:φm为船舶航向的理想系统性能;φr(t)为一个经过处理的命令输入信号,其值在0°~30°变化,周期为800 s。 在仿真中,选取控制器设计参数k1=20,k2=6,k4=1.2,σ=0.1,仿真结果见图1和图2。 图1 船舶航向历时曲线 图2 舵角历时曲线 由图1和图2可知:所设计的自适应神经网络控制器具有良好的适应性和鲁棒性,控制效果令人满意。 针对船舶航向控制系统中的非线性和不确定性,考虑输入饱和对系统稳定性的影响,在Backstepping算法的基础上融入神经网络控制技术,提出了一种符合工程实际的船舶航向控制算法。该算法的优点是鲁棒性好、参数易于调节,控制器的奇异值问题得到了有效解决,所设计的控制器结构简单,控制性能有保障。此外,在控制器设计过程中,饱和辅助设计系统及时对船舶航向非线性系统做了补偿,为系统的稳定性和控制性能提供了保障。 [1] 贾欣乐, 杨承恩, 颜德文. 自适应舵控制策略[J]. 大连海运学院学报, 1993, 19(2):179-188. [2] 胡耀华, 贾欣乐. 广义预测控制应用于船舶航向和航迹保持[J]. 中国造船, 1998(1):36-41. [3] 杨盐生. 不匹配不确定系统的变结构鲁棒控制及应用[J]. 交通运输工程学报, 2001, 1(2):103-107. [4] 贾欣乐, 张显库. H∞控制器应用于船舶自动舵[J]. 控制与决策, 1995, 10(3):250-254. [5] LI Junfang, LI Tieshan. Design of Ship's Course Autopilot with Input Saturation [J]. ICIC Express Letters, 2011, 5(10):3779-3784. [6] LI Junfang, LI Tieshan. Direct Adaptive NN Control of Ship Course Autopilot with Input Saturation [C]. Proceedings of the 4th International Workshop on Advanced Computational Intelligence, 2011. [7] LI Tieshan, WANG Dan, FENG Gang,etal. A DSC Approach to Robust Adaptive NN Tracking Control for Strict-Feedback Nonlinear Systems[J]. IEEE Transactions on Systems, Man, and Cybernetics,2010,40(3):915-927. [8] 王林, 陈楠, 高嵬. 基于Backstepping的船舶航向自适应滑模控制[J].船电技术, 2012,32(4):16-18. [9] KWAN C, LEWIS F L. Robust Backstepping Control of Nonlinear Systems Using Neural Networks[J]. IEEE Transactions on Systems, Man, and Cybernetics, 2000, 30(6):753-766. [10] 李俊方,李铁山. 考虑输入饱和的直接自适应神经网络跟踪控制[J]. 应用科学学报,2013, 31(3): 294-302. [11] CHEN M, GE S S. Neural Network Tracking Control of Ocean Surface Vessels with Input Saturation[C]. IEEE International Conference on Automation and Logistics, 2009. ModelFreeShipCourse-KeepingControl ZHANGYuxi Based on the backstepping technique, a direct adaptive neural network controller is proposed for the course-keeping control of ships with system uncertainties and input saturation. The radial basic function neural network is used as an approximation for the unknown system uncertainties and the possible instability caused by input saturation constrains is dealt with by an auxiliary design system. The algorithm is convenient to implement in engineering applications. The results of simulation show that the controller for ship motion control is effective in high precision ship course control. ship engineering; ship course control; input saturation; neural network; backstepping 2015-04-18 青年骨干教师基金(01780128) 张玉喜(1983—),男,黑龙江绥化人,讲师,研究方向为非线性控制、神经网络控制和船舶航向航迹控制等。 E-mail:mxtluck@163.com 1000-4653(2015)03-0009-04 U664.82;TP183 A2 控制器设计与稳定性分析
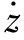
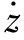
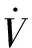
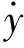
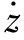

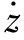


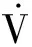
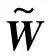

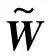


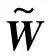
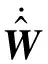
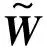
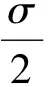
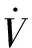

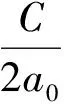
3 计算机仿真


4 结束语
(Navigation College, Dalian Maritime University, Dalian 116026, China)

