基于大口径火炮的实时弹道解算方法研究

秦鹏飞，崔青春，李 硕，刘爱峰，熊 涛

（西北机电工程研究所，陕西 咸阳 712099）

进入21世纪以来，随着高新技术的快速发展，战场侦察校射手段、战术机动性普遍增强，使得战场对抗空前加剧，这就对火炮火控系统提出了更高的要求，诸元解算是火控系统的核心任务之一［1］，所以必须在诸元解算的精度与速度两方面加以研究。实践证明，采用数值方法解弹道方程的方法能够提高诸元解算的精度，但相应地增加了诸元解算的时间。现行基于二分法的弹道解算方法虽然能满足目前火控系统的技术指标要求，但随着计算机技术的迅猛发展，对火控弹道诸元解算速度提出了更高要求，有必要对诸元解算的速度加以进一步研究。所以如何探索出一种能够提高解算速度的数值解算方法，是实现射击诸元实时解算的有待解决的难题之一。

在战场环境中根据作战要求，射击诸元解算是在已知目标坐标信息的条件下求解火炮射角和弹丸飞行时间，但此时无法直接为弹道方程组提供初始射角，导致无法对弹道方程组直接进行求解，所以使得该问题归结于微分方程的边值问题，即弹道求解的反问题［2］。在弹道模型确定的条件下，求解射击诸元的速度主要取决于对初始射角的估计、对弹道方程组求解和对射角进行迭代的速度三个方面［3］。因此，要提高诸元解算的速度，就必须针对初始射角的选取方法、弹道微分方程组的求解方法、射角修正的迭代方法三方面进行进一步研究。

1 弹道模型选择

弹道方程模型是弹道解算的基础和前提，直接影响着模型计算的速度与精度。弹道方程模型可以分为两类：一类是将弹丸作为质点研究的质点弹道模型；另一类是将弹丸作为刚体研究的刚体弹道模型［3］。质点模型不考虑弹丸在飞行过程中的姿态，而刚体模型考虑了在飞行过程中弹丸姿态的改变对弹道的影响。根据火炮种类的不同，在进行弹道计算时就需要选择不同的弹道方程模型［4］。笔者以某大口径火炮为例进行研究。由于该火炮射程相对较近、飞行过程中弹丸质量不发生变化，弹丸质心位置不发生变化，弹丸姿态变化对弹道的影响很小，所以可将其作为质点来考虑，采用弹丸质点运动方程弹道模型［5］。

数学模型如下：

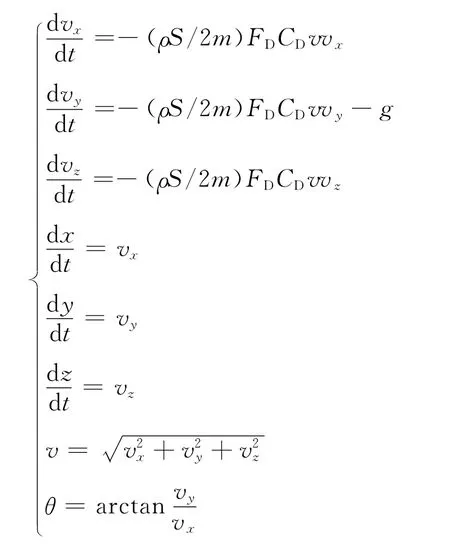
式中：vx、vy、vz分别为x、y、z方向弹丸飞行速度；ρ为空气密度；S为弹丸横截面积；m为弹丸质量；FD为弹道复合系数；CD为阻力系数；g为重力加速度。

2 现行基于二分法的弹道解算方法

现行基于二分法的弹道解算方法是将二分法的思想运用在求解火炮射击诸元的问题上（这里只考虑弹道低射界情况，在高射界区域可用同样方法求解）。具体方法如下：

1）根据炮目距离xc可以确定装药号数，从而确定火炮初速v0。

2）将最小射角θmin和最大射角θmax作为初始边界条件，初始射角选为θ0＝（θmin＋θmax）／2。

3）利用定步长的四阶龙格库塔法对弹道微分方程组积分得到射程x0，当x0＜xc时，令最小射角θmin不变，最大射角θmax＝θ0；当x0＞xc时，令最大射角θmax不变，最小射角θmin＝θ0。

4）取θ1＝（θmin＋θmax）／2作为下一次迭代的射角，积分得到对应射程X1，根据3）反复进行迭代。

5）直到第N次迭代后射程（xN－xc）＜ε，即得到射角θN及对应的弹丸飞行时间tN。

二分法解算示意图如图1所示。

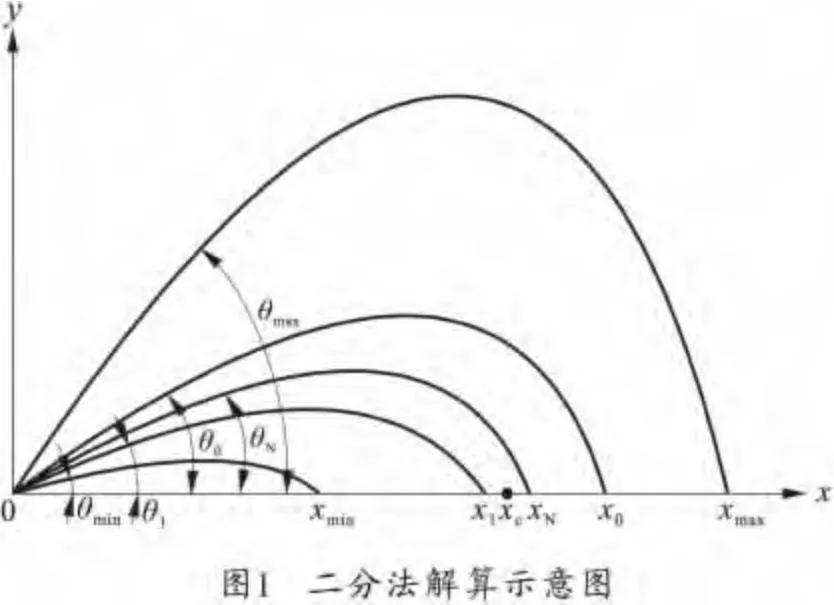
3 基于落点诸元信息的弹道解算方法

实践证明，现行的基于二分法求解射击诸元的方法已经能够满足目前火炮火控系统的技术指标要求，但为了进一步提高诸元解算速度，可以从该方法中得到几点启示：

1）初始射角的选取与目标的炮目距离没有关联性，往往使得初始射角与真实射角误差较大，导致迭代次数较多。

2）采用的定步长四阶龙格库塔法计算速度较慢。

3）使用二分法的修正方法收敛速度较慢。

为了提高弹道解算的速度，实现射击诸元实时解算的目标，根据现行二分法得出的3点启示，对弹道解算方法进行了针对性研究，探索出基于落点诸元信息的弹道解算方法，该方法的思想是：

1）根据已知射表，提取出1组射程与射角的相关数据，通过二次拟合的方法得到一个射程与射角的二次关系式。在进行实时射击诸元解算过程中，根据任意的射程就可得到与之相对应的初始射角，此射角与真实射角误差相对较小。

2）采用的变步长四阶龙格库塔法对弹道模型方程组进行数值计算，在一定程度上也提高了计算速度。

3）根据前一次的弹道积分得到落点的射程、速度信息，对后一次迭代射角进行修正，使得收敛速度得以提升。

基于落点诸元信息的弹道解算方法的具体方法如下：

1）根据目标坐标（XD，YD，ZD），可得到炮目距离进而可以确定装药号数，从而确定火炮初速v0。

2）在已知射表中，提取出1组射程（X1，X2，…，XN－1，XN）与射角（θ1，θ2，…，θN－1，θN）的数据，通过二次拟合得到一个射程与射角的关系式θ＝k2X2＋k1X＋k0；再根据炮目距离L，运用拟合的射程与射角关系式估计出初始射角θ01＝k2L2＋k1L＋k0；再根据目标坐标（XD，YD，ZD）及炮口坐标（0，0，0）可得到炮目高低角φ＝arctan（YD／XD）；最后得到初始射角θ0＝θ01＋φ。

3）再利用变步长的四阶龙格库塔法对弹道模型积分得到落点诸元信息射程xC、x方向速度vxC、y方向速度vyC。当xC＞xD时，射角修正量Δθ0≈Δy／xD＝（vyC／xxC）（xC－xD）／xD，此时若有误差距离Δx＝xC－xD，Δx＞100m 时，积分步长变为上步步长的2倍，反之变为上步步长的0.5 倍；当xC≤xD时，同样方法处理。

4）取θ1＝θ0－Δθ0作为下一次迭代的射角，利用变步长积分得到对应射程x1，根据3）反复进行迭代。

5）直到第N次迭代后得到落点的射程xN，且xN－xD＜ε（误差允许值），即得到射角θN及对应的弹丸飞行时间tN。

射角迭代示意图如图2所示。图中O点为炮口所在位置，D点为目标所在位置，x轴为弹丸飞行射程方向，y轴为弹丸飞行高程方向。

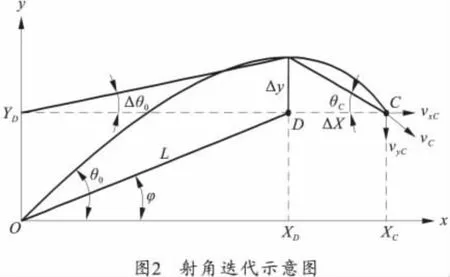
4 程序仿真验证

以某大口径火炮为研究对象，分别在标准条件与非标准条件下对解算方法进行仿真验证。各参数定义为：弹径为d、弹丸质量为m、空气阻力系数参照1943年的标准空气阻力系数、重力加速度为9.8 m／s2、全装药条件下初速为v0。

假设条件如下：

1）在标准条件下，炮口坐标为（0，0，0），目标坐标为（2 800，50，0）。

2）在非标准条件下，炮口坐标为（0，0，0），目标坐标为（6 800，50，0），纵风速度为10m／s。

分别应用Matlab数值仿真软件对基于落点诸元信息的弹道解算方法进行仿真验证（这里不再对基于二分法的弹道解算方法进行仿真，该方法在文献［6］中有详细介绍），具体方法如下：

1）对初始射角进行估计。

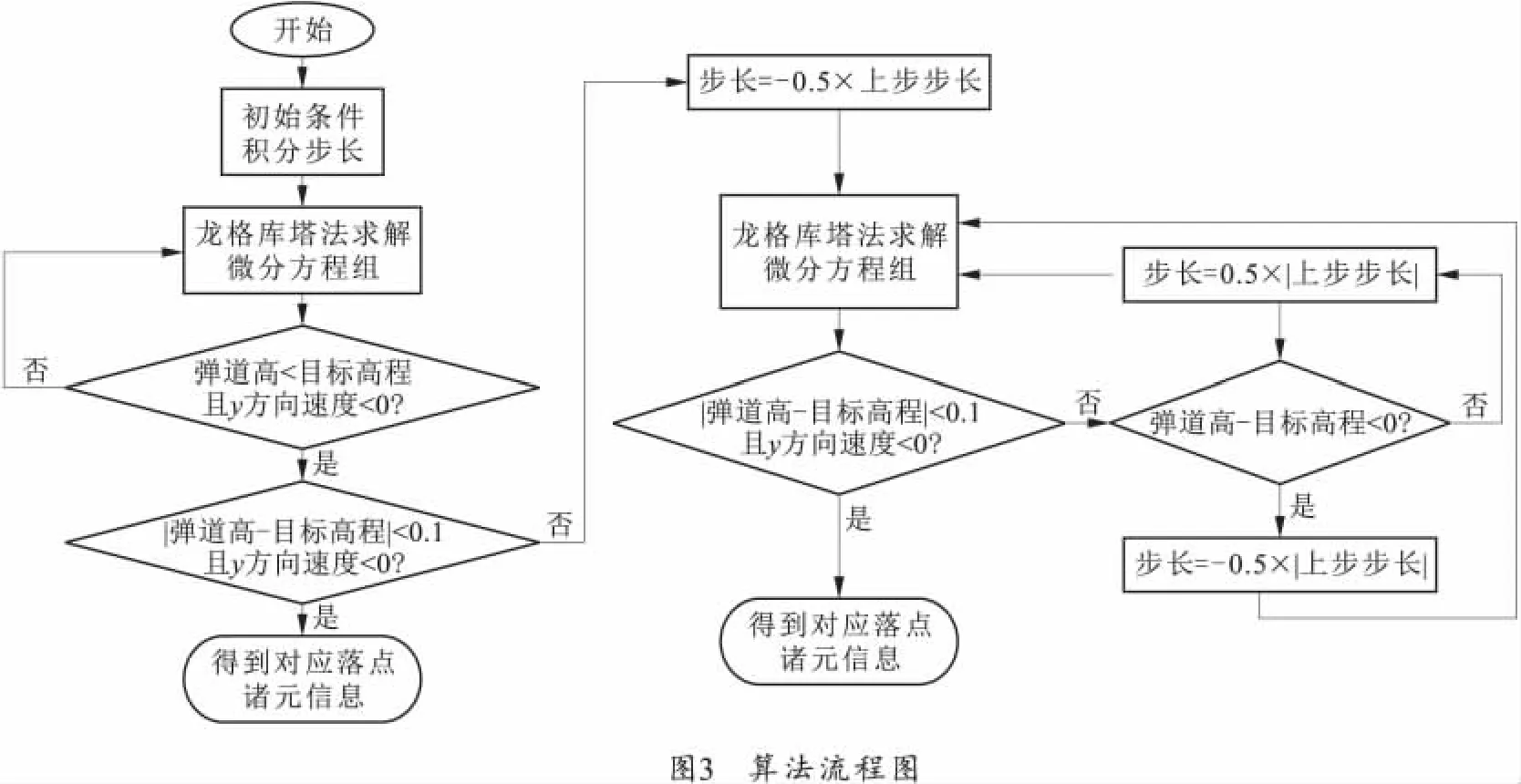
2）应用变步长的四阶龙格库塔法对弹道微分方程组进行求解，得到落点诸元信息的射程xC、x方向速度vxC、y方向速度vyC、从而可得射角修正量Δθ0。算法流程图如图3所示。

3）通过反复对射角的迭代解算，最终得到所需射角与弹丸飞行时间。射角迭代流程图如图4所示。

5 仿真结果分析

5.1 标准条件下仿真结果

利用二分法解算方法求解出的弹道迭代曲线如图5所示。虚线表示中间迭代过程的弹道曲线，实线表示最终命中目标的弹道曲线。

利用落点诸元信息解算方法求解出的弹道迭代曲线如图6所示。

对两种解算方法进行仿真计算得出的重要参数如表1所示。

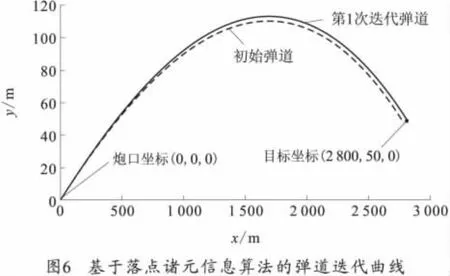
表1 两种解算方法解算的结果

通过对仿真结果的分析，采取基于落点诸元信息的解算方法相对于基于二分法的解算方法有以下几点改进：

1）在对初始射角估计方面，θ0＝120.083mrad，已经较接近于射角真值θ0＝121.601 8mrad。

2）在迭代次数方面，仅需要1次迭代修正就能找到所需射角，大大减少了迭代次数。

3）在解算时间方面，使用同1台计算机进行仿真计算时，仅需0.098s的解算时间，足以表明解算时间有大幅度缩减。

5.2 非标准条件下仿真结果

利用二分法解算方法求解出的弹道迭代曲线如图7所示。图中虚线表示中间迭代过程的弹道曲线，实线表示最终命中目标的弹道曲线。

利用落点诸元信息解算方法求解出的弹道迭代曲线如图8所示。图中虚线表示中间迭代过程的弹道曲线，实线表示最终命中目标的弹道曲线。

对两种解算方法进行仿真计算得出的重要参数如表2所示。

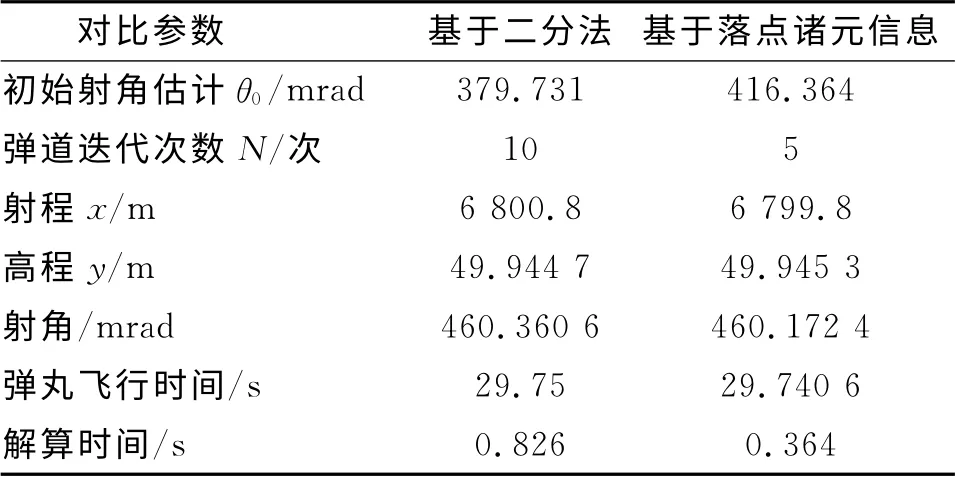
表2 两种解算方法解算的结果

通过对仿真结果的分析，得到与标准条件下相似的结论。在对初始射角估计方面、迭代次数方面、解算时间方面都得到了一定的改进。

6 结束语

通过对火炮射击诸元实时弹道解算方法的研究，分析了对弹道解算速度的影响因素。根据在现行的基于二分法的弹道解算方法中得到的几点启示，并针对这几点启示进行了进一步的理论研究，探索出了一种新的火炮射击诸元解算方法，通过对新的基于落点诸元信息的弹道解算方法的理论研究与仿真验证，得出这种新的解算方法能既能够保证解算的精度又能大幅度地缩短弹道解算时间，对实现火炮射击诸元的实时解算有着重要参考价值。

（References）

［1］周启煌，常天庆，邱晓波.战车火控系统与指控系统［M］.北京：国防工业出版社，2003.ZHOU Qihuang，CHANG Tianqing，QIU Xiaobo.Fire control system and command control system of combat vehicle［M］.Beijing：National Defense Industry Press，2003.（in Chinese）

［2］王敏忠.炮兵应用外弹道学及仿真［M］.北京：国防工业出版社，2009.WANG Minzhong.Artillery applied exterior ballistics and simulation［M］.Beijing：National Defense Industry Press，2009.（in Chinese）

［3］钱林方.火炮弹道学［M］.北京：北京理工大学出版社，2009.QIAN Linfang.Ballistics of cannon［M］.Beijing：Beijing Institute of Technology Press，2009.（in Chinese）

［4］赵新生.弹道解算理论与应用［M］.北京：兵器工业出版社，2006.ZHAO Xinsheng.The theory and application of trajectory calculation［M］.Beijing：The Publishing House of Ordnance Industry，2006.（in Chinese）

［5］韩子鹏.弹箭外弹道学［M］.北京：北京理工大学出版社，2008.HAN Zipeng.Rocket external ballistics［M］.Beijing：Beijing Institute of Technology Press，2008.（in Chinese）

［6］秦鹏飞.基于二分法的实时弹道解算方法研究［C］∥陕西省兵工学会第十七届学术年会.西安：陕西省兵工学会，2013.QIN Pengfei.Research on the real－time ballistic algorithm based on method of bisection［C］∥The Academic Annual Meeting of the Seventeenth Shaanxi Ordnance Society.Xi’an：Shaanxi Ordnance Society，2013.（in Chinese）