基于ADC模型的点目标最佳CEP求解

宋谢恩，宋卫东，吴汉洲

（军械工程学院 火炮工程系，河北 石家庄 050003）

火箭弹经过弹道修正后，射击精度明显提高，甚至可对点目标进行射击［1］。圆概率误差（Circle Error Probability，CEP）作为射击精度的重要衡量指标，等于概率为50%的圆形误差范围的半径［2］。由于点目标与面目标的射击方式、幅员大小等不同，故其对于射击精度的需求也不同。针对于点目标的CEP需求，笔者基于作战效能理论和射击毁伤理论，考虑实战条件，确立了点目标最佳CEP 的求解方法，采用固定效能法，分析了CEP 变化对毁伤概率和射击成本等产生的影响，得出了点目标的CEP需求规律。

1 最佳CEP求解模型

1.1 最佳CEP的提出

在不考虑外界约束的情况下，CEP越小射击精度越高，射击效果越好［3］。但在受到成本、目标毁伤幅员等条件约束时，CEP不再是越小越好。故在实际条件约束下，存在最佳CEP，能够在满足射击任务要求的前提下实现成本最低。

1.2 WSEIAC系统效能模型

美国空军武器系统效能工业咨询委员会（WSEIAC）把系统效能定义为：系统能满足一组规定任务要求之程度的量度，它是可用度、可信赖度及能力的函数。表达式为

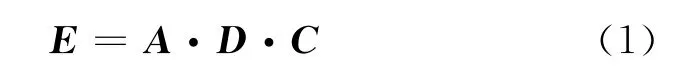
式中：E为系统效能；A为可用度，即系统在开始执行任务时处于可用状态的概率；D为可信赖度，即在给定的系统所处初始状态下，系统在执行任务过程中所处状态的量度；C为能力，即已知系统在执行任务过程中所处的状态时，系统完成规定任务的量度，如毁伤概率等［4］。

研究对象为弹道修正火箭弹，其状态分为“正常工作”和“发生故障”两种。这时，系统的可用度、可信赖度和能力分别表示为

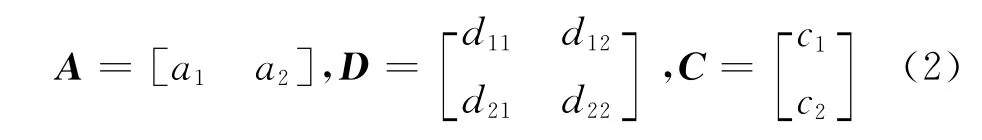
显然，d21＝0，d22＝1，c2＝0，则系统的效能向量E可表示为［5］

a1、d11、c1包含了诸如发现目标概率、生存概率、命中概率、可靠性等多方面的因素，且这些因素为串联关系，故

式中，P1为第i项因素的概率。

本文主要研究CEP 变化影响的可靠性因素P1、命中概率P2，可将式（4）转化为

1.3 命中概率计算模型

火箭弹落点散布服从正态分布，设修正弹落点坐标为（x，z），x～N（μx，σ2x），z～N（μz，σ2z）。修正弹CEP以目标点为中心，故μx＝μz＝0。假定纵横向落点相互独立，采用射击落点圆散布模型，σx＝σz＝σ。设δCEP为圆概率误差的量符号，其与纵、横向射击精度有近似的关系式［6］：

设目标的毁伤幅员［7］半径为R，当火箭弹落点（x，z）与目标点（0，0）距离小于毁伤幅员半径时，目标即被命中。所以单发射击命中目标点概率为

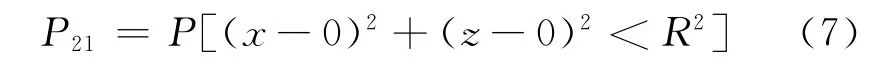
令χ2α（2）＝R2／σ2，由概率论卡方分布可将式（7）转换为［8］

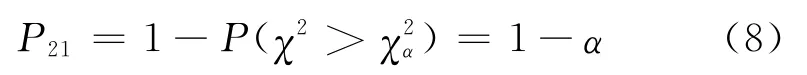
射击N发命中概率为

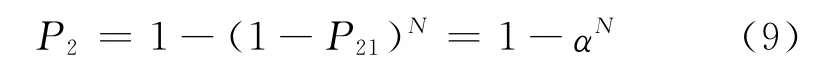
毁伤概率P＝P1P2。

1.4 效费比计算模型

效费分析是武器系统研制开发过程中的重要环节，其目的在于寻求效能与费用的最优方案［9］。效费比计算公式［10］：

全寿命费用T＝T0＋T1，其中T1为修正弹成本，T0为其他费用。采用固定效能法进行分析：规定要求的效能水平，估算各方案完成任务的费用。费用最少的方案被认为是最优方案。

总结以上方法可得，对点目标射击最佳CEP求解，即求解达到相同毁伤概率P时，最少修正弹成本T1对应的δCEP。

2 最佳CEP求解

2.1 计算初始条件

弹道修正火箭弹对点目标射击时采用集火射击方式；设对不同种类目标的有效毁伤半径分别为30、20、10、5、3、2m［7］；δCEP从50m等差递减到1m；毁伤概率要求P为0.9、0.5、0.3。不同δCEP的修正弹单发成本T11：由于成本限制，根据可靠性理论［11］得出不同δCEP的修正弹可靠性P1不同：

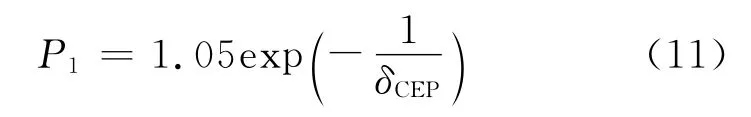
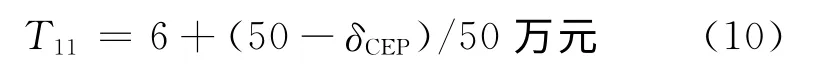
2.2 计算结果及分析

按照建立的最佳CEP求解模型进行运算，R＝30m、P＝0.9时，计算结果如图1～图5所示。随着δCEP变大，单发修正弹对目标点的毁伤概率先变大后变小，完成射击任务所需弹药量随之先变小后变大，修正弹总成本也是先变小后变大，其极值点如图5中A点（12，7.8），即R＝30m、P＝0.9对应的最佳δCEP为12 m，最小修正弹成本为7.8万元。图3曲线为图1、图2两曲线的乘积，随着δCEP增大，命中概率变小而可靠性变大时。当δCEP＜12m时，可靠度为主导因素，δCEP＞12 m 命中概率为主导因素。所以毁伤概率曲线有上述变化。

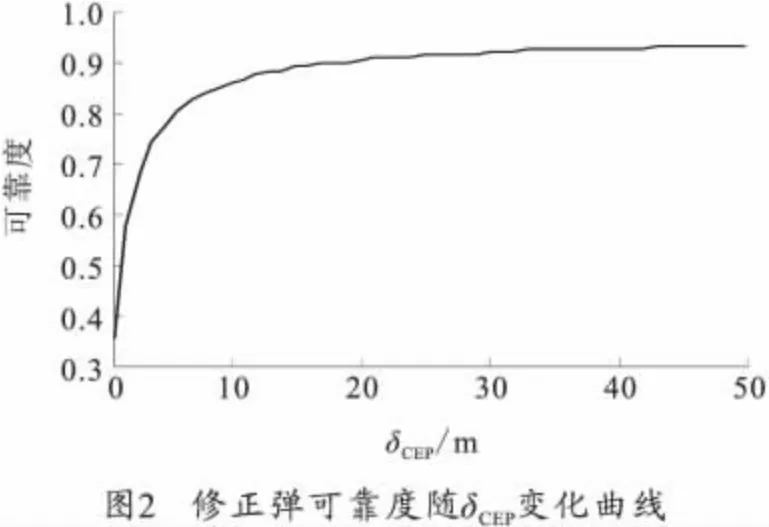
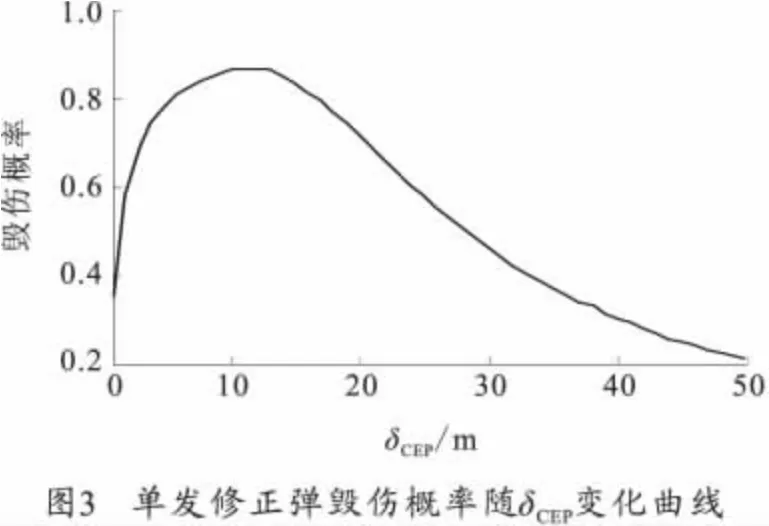
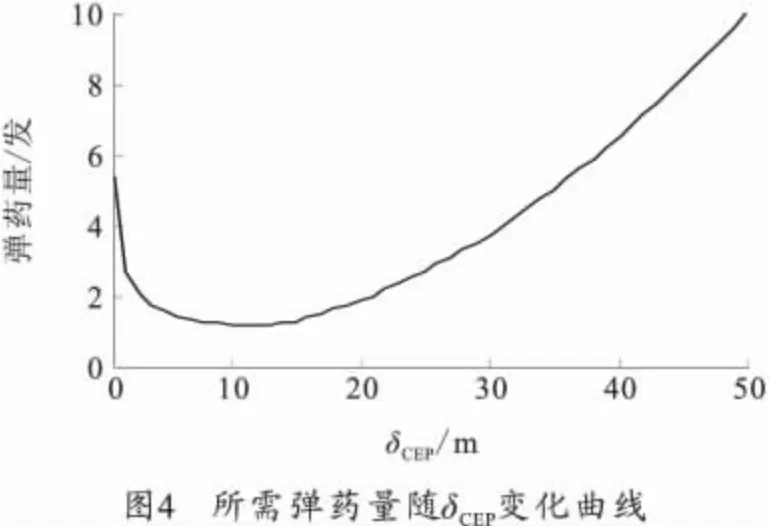
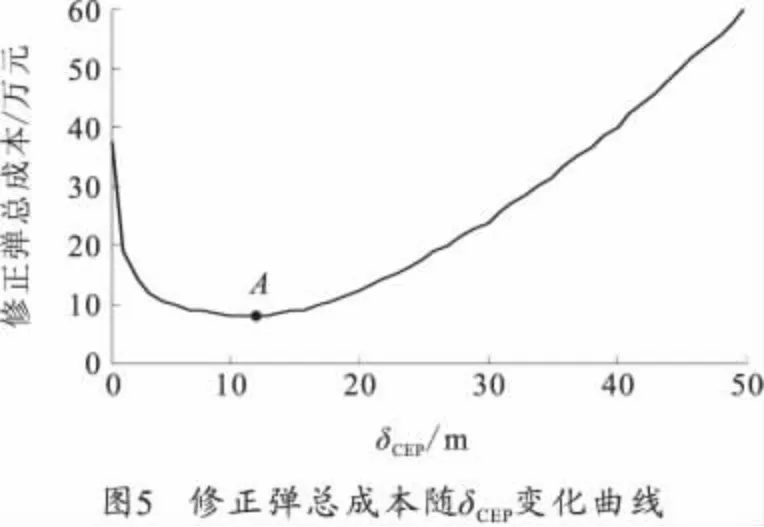
当R和P变化时，对应的图2不变，对应的图1、图3～图5的变化规律一致，仅数值变化。不同R和P对应的最佳CEP 如表1～表3所示。纵向对比，对于同一毁伤幅员R，最佳CEP相等，总成本随着毁伤概率要求的减小而减小。横向对比，对于同一毁伤概率要求，随着毁伤幅员变大，最佳δCEP变大，而总成本随之降低。综合3 个表数值可得出，火箭弹在经过弹道修正后，适合攻击毁伤幅员较大或者毁伤概率要求不高的目标，对于毁伤幅员较小且毁伤概率要求较高的目标，射击成本过高，不适合作为火箭弹的攻击目标。

综合分析结果和无控火箭弹作战使命，推断火箭弹在经过弹道修正后攻击的点目标一般为简易装甲等易损性目标，毁伤幅员较大，毁伤概率要求较高，故得出修正弹设计指标δCEP＝10m。

表1 P＝0.9时的最佳CEP

表2 P＝0.5时的最佳CEP

表3 P＝0.3时的最佳CEP

3 结论

笔者基于ADC效能求解模型，将CEP对火箭炮武器系统效能影响转化为对命中概率、可靠性的影响，采用效费分析中的固定效能法，分析了不同射击条件下的CEP变化对毁伤概率和射击成本等产生的影响，最终得出了为攻击点目标进行弹道修正后的火箭弹适合攻击毁伤幅员较大或者毁伤概率要求不高的目标，不适合攻击毁伤幅员较小且毁伤概率要求较高的目标，并推断弹道修正火箭弹对点目标射击时的最佳CEP 为10 m 左右。毁伤概率、效费比的计算方法和最佳CEP 的确定思路为其他武器系统的效能分析和相关设计指标确定提供了参考。

（References）

［1］张民权，刘东方，王冬梅，等.弹道修正弹发展综述［J］.兵工学报，2010，31（2）：127－130.ZHANG Minquan，LIU Dongfang，WANG Dongmei，et al.A summary for trajectory correction projectiles［J］.Acta Armamenterii，2010，31（2）：127－130.（in Chinese）

［2］国防科学技术工业委员会.GJB102A－1998 弹药系统术语［S］.北京：国防科学技术工业委员会军标出版发行部，1987：3.National Defense Science and Technology Industrial Committee.GJB102A－1998Nomenclature of amnmnition system［S］.Beijing：Military Standard Publishing Department of National Defense Science and Technology Industrial Committee，1987：3.（in Chinese）

［3］郭锡福.远程火炮武器系统射击精度分析［M］.北京：国防工业出版社，2004：1－4.GUO Xifu.Firing accuracy analysis for long range gun weapon systems［M］.Beijing：National Defense Industry Press，2004：1－4.（in Chinese）

［4］罗兴柏，刘国庆.陆军武器系统作战效能分析［M］.北京：国防工业出版社，2007：10－19.LUO Xingbai，LIU Guoqing.Analysis of operational effectiveness for army weapon system［M］.Beijing：National Defense Industry Press，2007：10－19.（in Chinese）

［5］李廷杰.导弹武器系统的效能及其分析［M］.北京：国防工业出版社，2000：34－35.LI Tingjie.Effectiveness analysis for missile weapon systems ［M］.Beijing：National Defense Industry Press，2000：34－35.（in Chinese）

［6］姚志军.多管火箭射击精度试验方法研究［D］.南京：南京理工大学，2008.YAO Zhijun.Firing accuracy test method of multiple launch rocket system［D］.Nanjing：Nanjing University of Science and Technology，2008.（in Chinese）

［7］郑津生.炮兵射击理论研究与应用［M］.北京：中国人民解放军出版社，1995：178－183.ZHENG Jinsheng.Gunnery theory study and application［M］.Beijing：The PLA Publishing House，1995：178－183.（in Chinese）

［8］闫章更，魏振军.试验数据的统计分析［M］.北京：国防工业出版社，2001：22－26.YAN Zhanggeng，WEI Zhenjun.Statistical analysis of geotechnical test data［M］.Beijing：National Defense Industry Press，2001：22－26.（in Chinese）

［9］王玉泉.装备费用效能分析［M］.北京：国防工业出版社，2010：1－3.WANG Yuquan.Cost－effectiveness analysis for materiel［M］.Beijing：National Defense Industry Press，2010：1－3.（in Chinese）

［10］王珂晟，邹永显，李永东，等.试论武器装备的效费比分析［J］.装甲兵工程学院学报，2003，17（3）：55－58.WANG Kesheng，ZOU Yongxian，LI Yongdong，et al.Analysis on proportion of effectiveness and life cycle cost of weapon equipment［J］.Journal of Academy Armored Force Engineering，2003，17（3）：55－58.（in Chinese）

［11］姜兴渭，宋政吉，王晓晨.可靠性工程技术［M］.哈尔滨：哈尔滨工业大学出版社，2005：26－31.JIANG Xingwei，SONG Zhengji，WANG Xiaochen.Reliability engineering technology［M］.Harbin：Harbin Institute of Technology Press，2005：26－31.（in Chinese）