基于概率法与有限元法的火炮方向机齿轮传动误差分析

李 忠，韩崇伟，赵宇和，石志翔，彭 超

（西北机电工程研究所，陕西 咸阳 712099）

齿轮传动是现代机械产品中十分常见的传动机构，广泛应用于航天航空、舰船、火炮、机床等许多大中型工业机器中。齿轮传动的误差直接影响了运动传递的准确性，进而影响整个机械的性能。火炮方向机是一种典型的齿轮传动机构，笔者分析了火炮方向机齿轮传动过程中产生的静态传动误差和动态传动误差，推导了齿轮传动总误差的计算公式，同时得到了方向机在不同载荷下动态误差曲线，可为研究火炮方向机对调炮精度的影响提供参考。

1 影响齿轮传动误差的因素

传动误差是指输入轴单向回转时，输出轴转角的实际值相对于理论值的变动量［1］。在理想的传动过程中，输入轴转角φi与输出轴转角φo之间应该符合理想的传动关系，即

式中，i为传动结构的总传动比。

在齿轮传动的过程中，影响齿轮传动误差的因素主要有齿轮本身的加工误差、齿轮的装配偏差以及齿轮在传动过程中的磨损误差，在实际工作中通过定期检修，可以调整由于磨损造成的齿轮啮合间隙，因此文中暂不考虑齿轮磨损对齿轮传动误差的影响［2］。而影响齿轮传动链误差的主要因素除了因齿轮制造和装配不绝对准确造成的单向传动误差和回程误差等静态传动误差外，还有传动齿轮与传动轴因受负载转矩而产生扭转变形和弯曲变形导致的动态传动误差，它随着负载转矩的大小而改变。由上可知，齿轮传动链的传动误差是由齿轮本身、所在轴和轴承等零部件制造装配时的误差，以及受负载转矩时产生动态误差等综合作用的结果。

2 齿轮传动的静态误差分析

齿轮静态传动误差的来源主要是齿轮的制造误差和安装误差。齿轮制造误差是由于齿轮制造时几何偏心、运动偏心、齿形误差和齿厚偏差等因素综合作用形成。齿轮安装误差是由于齿轮实际回转中心相对理论回转中心的偏离引起的，主要影响因素有中心距偏差、齿轮与轴的配合间隙和轴承的径向游隙。

2.1 单向传动误差

齿轮传动的单向传动误差主要是由切向综合总偏差F′i引起，切向综合总偏差作为大周期误差反映了齿轮几何偏心和运动偏心导致的静态传动误差。记为

由机械设计手册［3］查得：

式中：Fp为齿距累积总偏差的公差；f′i为一齿切向综合偏差。

所以，一对啮合齿轮副的单向传动误差角φ为

式中：K1、K2分别为相互啮合的两个齿轮的单向传动误差；d2为从动轮的分度圆直径。

2.2 空回误差

齿轮传动的空回误差，就是当主动轮反向转动时从动轮相对滞后主动轮的转角，其原因主要是由于齿轮的齿厚偏差、中心距偏差和轴承游隙等因素导致齿轮啮合产生圆周侧隙，从而引起传动空回［4］。

1）齿厚偏差导致的圆周侧隙

为了补偿齿轮制造和安装误差，热膨胀变形以及便于润滑所留齿侧间隙，可以根据齿厚偏差来确定。一对齿轮副由此而产生的侧隙为

式中，Es1、Es2分别为两个齿轮的实际偏差值。

2）中心距偏差导致的圆周侧隙

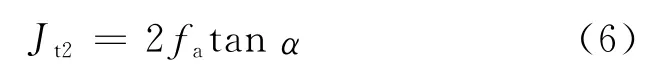
式中，fa为中心距偏差值，等于实际中心距减去理论中心距；α为压力角。

3）轴承游隙导致的圆周侧隙

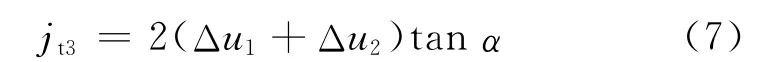
式中，Δu1、Δu2分别为两齿轮支撑轴承的径向游隙。

由此可知，一对齿轮副的空回误差为

式中，jt为齿轮副的圆周侧隙。

由于齿轮传动静态传动误差的随机性，各项误差是相互独立的且服从正态分布，根据经验，误差随机量落在±3σ范围里的置信率为99.74%，根据概率论理论得到齿轮传动静态传动误差的数字特征［5］为

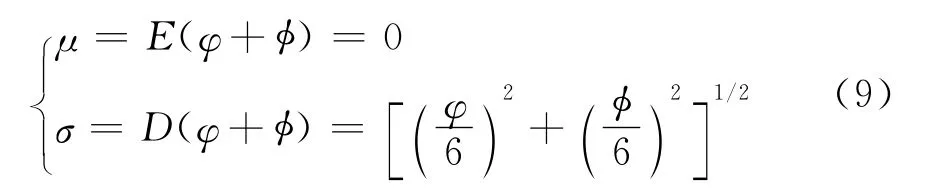
式中：E为齿轮静态传动误差的期望；σ为齿轮静态传动误差的标准差。

所以取齿轮副的静态传动误差

齿轮传动系统的静态传动误差是由各级齿轮副的误差逐级叠加而成，通过传动比折算到末级齿轮上，考虑到各级误差的随机性，则

式中，i2，i3，…，ik为各级齿轮副的传动比。

3 齿轮传动的动态误差分析

齿轮传动时，由于传递转矩的增大，以及传动轴和齿轮材料的刚度不足，会导致传动过程中传动轴和齿轮的弹性扭转变形，使转动角产生滞后，从而引起齿轮传动动态传动误差。

3.1 传动轴的扭转变形

根据材料力学［6］的相关知识可知：当转动轴受到扭矩T时，传动轴的扭转变形为

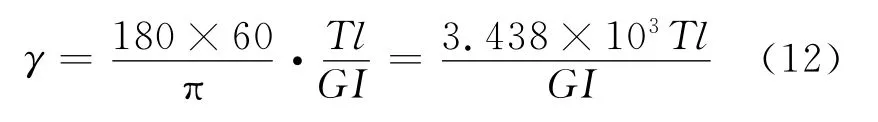
式中：T为轴承受的扭矩；l为轴的长度；G为材料的剪切模量；I为轴的极惯性矩；其中GI／l被称为扭转刚度，在实际的工程设计中，为了节省材料，传动轴通常为阶梯轴，其等效扭转刚度为ke。则式（12）变为

所以，齿轮传动系统因传动轴的扭转变形产生的动态传动误差为

3.2 传动轴的弯曲变形

在齿轮传动过程中，在齿面法向力Fn的作用下，传动轴会发生弯曲变形，变形方向与齿轮传动的啮合线方向相一致，如图1所示。

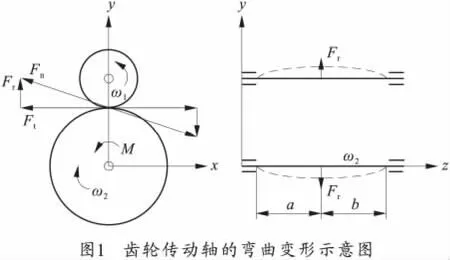
根据轴的弹性弯曲变形理论［3］可得，传动轴在齿轮位置沿啮合线方向的弹性变形量为

式中：Fn为法向啮合力；a、b为齿轮到两轴承端的距离；E为弹性模 量；dz为轴的直径。

通常将其分解为切向分量和法向分量，由此导致齿轮传动副产生的圆周侧隙有如下关系：

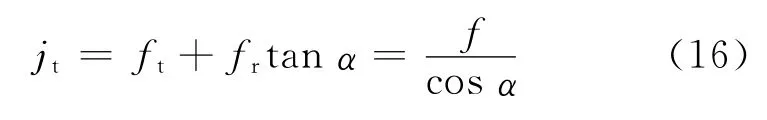
式中：ft为传动轴弯曲变形的切向分量；fr为传动轴弯曲变形的径向分量。

所以，传动轴的弯曲变形导致一对齿轮传动副的动态传动误差角为

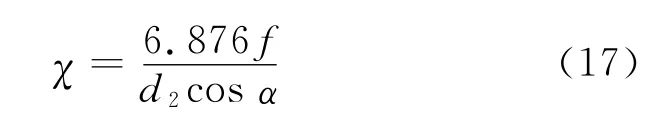
当反向传动时，传动轴会出现沿啮合线反方向的弯曲变形，从而引起的回差应该为2χ。齿轮传动系统因传动轴的弯曲变形产生的动态传动误差为

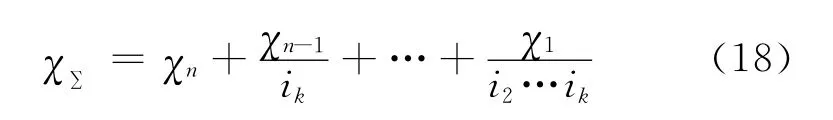
3.3 齿轮的扭转变形

齿轮传动是圆周运动的传动，从误差传递方法考虑，有学者提出了扭转啮合刚度理论［7］，定义扭转刚度km为：齿轮承受的扭矩载荷T和在该扭矩载荷作用下轮体产生的弹性扭转角θ之间的比值。

齿轮的扭转变形主要包括3部分：轮毂扭转、轮齿弯曲变形和齿面接触变形，这3种变形综合起来对齿轮传动的误差可以用齿轮在分度圆上的扭转变形角来描述，如图2所示。因此，要获得齿轮扭转啮合刚度就需要得知齿轮在该载荷下的扭转变形角位移［8］。

以直齿圆柱齿轮为例，利用有限元分析软件Ansys workbench分析齿轮在齿面法向Fn作用下的扭转变形角位移［9－10］。

对轮齿受力分析，齿轮受到圆周力、径向力和法向力，有如下关系式：

式中，T为齿轮受到的扭矩。

根据式（19），可以得到作用于轮齿齿面的法向力Fn。

齿轮的载荷与约束情况：在齿内圈面A 添加固定约束，在齿面B添加法向力，如图3所示。

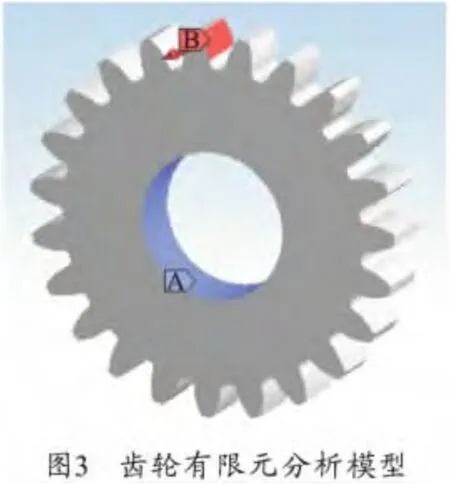
根据仿真分析云图，得到齿顶的扭转变形xa和齿根的扭转变形xf，利用插值法得到分度圆的扭转变形角位移为

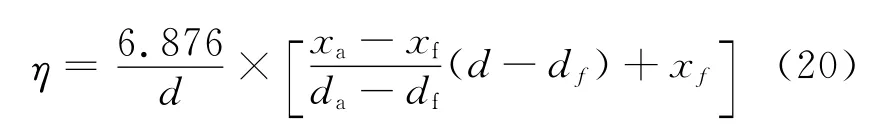
式中：d为齿轮分度圆直径；da为齿轮齿顶圆直径；df为齿轮齿根圆直径。

因为齿轮传动的过程中单齿啮合和双齿啮合是相互交替进行的［11］，从单齿过渡到双齿时，齿轮的变形会逐渐变小，取齿轮的等效扭转刚度为kme，所以齿轮的扭转变形角为

式中，εα为重合度。

齿轮传动系统因齿轮的扭转变形产生的动态传动误差为

所以，齿轮传动链的动态传动误差为

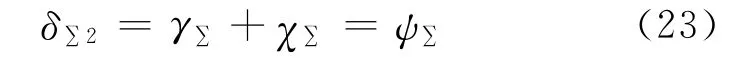
综上所述，在齿轮链传动过程中，齿轮传动总误差由静态传动误差和动态传动误差组成，即

4 实例分析

以某型火炮方向机的传动机构为例，采用上述误差分析方法，计算该方向机的传动误差，将计算结果与实际传动误差比较。

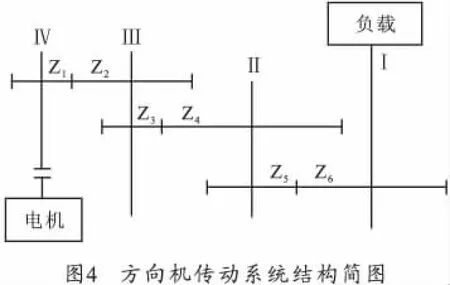
方向机传动机构主要参数如下：火炮炮塔水平方向上的转动惯量J＝11 331kg·m2，角加速度α＝70（°）／s2，负载的转动扭矩T＝931.13N·m，齿轮与轴的材料弹性模量E＝2.06×1011Pa，剪切模量G＝7.9×1010Pa，泊松比μ＝0.3。齿轮链中传动齿轮的主要参数如表1所示。

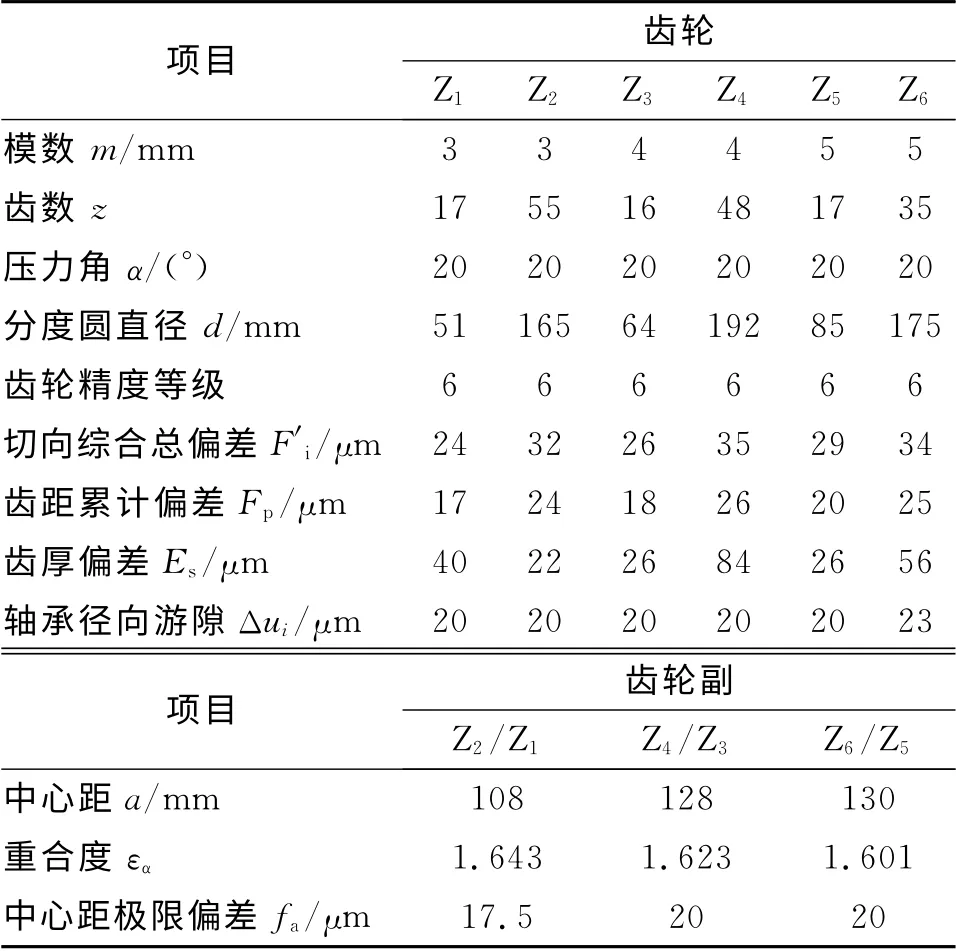
表1 齿轮链的主要参数

4.1 方向机静态误差的计算

根据表1中数据可知方向机传动机构各级传动齿轮的单向传动误差K1与K2，圆周侧隙jt以及从动轮的分度圆直径d2等参数如表2所示，由式（4）以及（8）～（11）计算得到方向机的静态传动误差如表2所示。

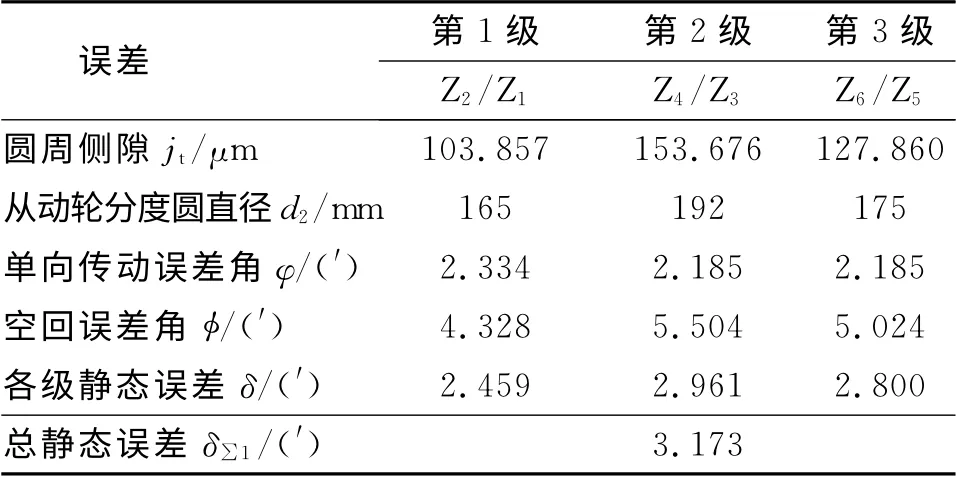
表2 方向机的静态误差

所以，由于制造和安装等因素的影响，方向机的传动齿轮的静态传动误差为δ∑1＝3.173。

4.2 方向机动态误差的计算

方向机传动结构的各传动轴受到的扭矩如表3所示。

表3 传动轴受到的扭矩

根据式（12）计算各级传动轴的扭转变形如表4所示。

表4 传动轴的扭转变形角

代入式（14），得到方向机传动轴由于扭转变形而产生的动态传动误差角为γ∑＝5.292。

下面计算方向机传动轴在齿面法向力作用下产生的弯曲变形。首先，根据表3中传动轴受到的扭矩和式（19），可以计算得到各传动齿轮受到法向力Fn，如表5所示。

表5 方向机传动齿轮受到的法向力

根据3.2节的传动轴弯曲变形分析方法，分析传动轴Ⅰ的受力情况，如图5所示。

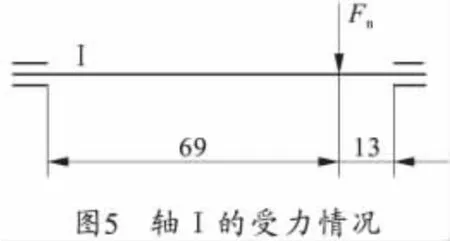
将参数代入式（16），得到传动副齿轮Z5与Z6之间的圆周侧隙f＝0.562，再代入式（17）得到，由于传动轴Ⅰ弯曲变形导致齿轮Z5与Z6的动态传动误差角χ1＝0.047。

同理，可以计算得到第2级传动齿轮Z3与Z4的传动误差角χ2＝0.216，以及第1级传动齿轮Z1与Z2的动态传动误差角χ3＝0.015。

代入式（18），计算得到方向机齿轮传动系统因传动轴的弯曲变形而产生的动态传动误差χ∑＝0.154。

可见，初级传动轴和末级传动轴的弯曲变形导致的传动误差是很小的，这是由于在安装设计过程中，将初级轴上的齿轮与末级轴上的齿轮靠近支撑轴承安装，减小了轴的弯曲变形，进而减小了对齿轮传动精度的影响。

下面采用有限元方法，根据方向机传动齿轮所受到的负载，计算方向机传动时因齿轮变形引起的动态传动误差。

利用三维建模软件UG 的参数化建模功能，建立传动链齿轮的三维模型，导出Parasolid的.x＿t文件，再导入有限元分析工具Ansys workbench中，对齿轮的受力变形进行分析，得到传动齿轮的仿真结果如图6所示。

根据上面的仿真分析云图，可知方向机传动链齿轮在负载扭矩作用下各齿轮的齿顶圆与齿根圆的变形位移，代入式（20），计算得到齿轮分度圆的变形角位移，即是测量点的变形角位移。再由式（21）～（23），计算得到齿轮的扭转变形角，结果如表6所示。

表6 传动链齿轮的变形位移

由式（24）计算得到方向机传动由于齿轮扭转变形而产生的动态传动误差ψ∑＝1.091。

综上所述，当炮塔角加速度为70（°）／s2时，方向机的动态传动误差δ∑2＝6.537。

4.3 方向机传动总误差的计算

根据上述总结的齿轮传动误差计算方法，最后得到该方向机的传动误差如表7所示。

表7 方向机的传动误差

所以，方向机在该负载作用下的传动总误差为9.71′，与工程实际误差值8′～10′相符。

火炮在跟踪瞄准射击目标的过程中，炮塔的调转角加速度是变化的，那么方向机的负载也应该是变化的，因此方向机传动结构的动态传动误差随着负载的变化而变化。利用上述动态传动误差的计算方法，分别计算炮塔的调转角加速度为10（°）／s2，20（°）／s2，…，70（°）／s2时，方向机传动的动态传动误差分别如表8所示。

表8 不同调转角加速度下方向机动态传动误差

利用Matlab的数据拟合功能，得到方向机动态传动误差在炮塔不同调转角加速度下的变化曲线如图7所示。

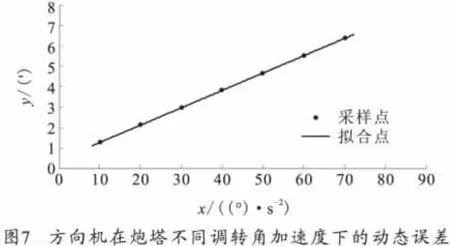
拟合曲线为：

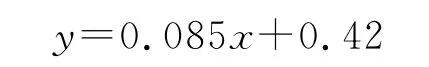
式中：x为炮塔调转角加速度；y为方向机的动态传动误差。

综上所述，方向机的传动总误差可以写成：

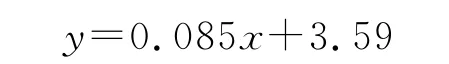
5 结论

根据齿轮传动制造与安装误差的正态分布规律，采用概率法分析了火炮方向机齿轮传动的静态传动误差；采用有限元法，仿真分析了火炮方向机齿轮传动结构在不同载荷下的动态扭转变形，得到了方向机传动动态传动误差在炮塔不同调转角加速度下的变化曲线，最后得出了传动总误差与炮塔调转角加速度的关系式，可为研究火炮方向机对调炮精度的影响提供参考。

（References）

［1］李蕾.精密机械设计［M］.北京：化学工业出版社，2005.LI Lei.Design of precision machinery［M］.Beijing：Chemistry Industry Press，2005.（in Chinese）

［2］李聚波，贺红霞，张洛平，等.齿轮传动精度的分析与计算［J］.煤矿机械，2006，27（7）：18－20.LI Jubo，HE Hongxia，ZHANG Luoping，et al.Analysis and calculation of precision of gear transmission［J］.Coal Mine Machinery，2006，27（7）：18－20.（in Chinese）

［3］成大先.机械设计手册［M］.北京：化学工业出版社，2010.CHENG Daxian.Mechanical design manual［M］.Beijing：Chemistry Industry Press，2010.（in Chinese）

［4］周广武，王家序，李俊阳，等.滤波减速器回差分析与精度控制［J］.中国科技论文在线，2010，5（8）：608－614.ZHOU Guangwu，WANG Jiaxu，LI Junyang，et al.Analysis and control on the backlash of filtering gear reducer［J］.China Science Paper Online，2010，5（8）：608－614.（in Chinese）

［5］林长洪，朱家诚.齿轮传递误差计算的分析［J］.设计与研究，2011，8（38）：10－13.LIN Changhong，ZHU Jiacheng.The calculation of transmission error of gear［J］.Design and Research，2011，8（38）：10－13.（in Chinese）

［6］胡益平.材料力学［M］.四川：四川大学出版社，2011.HU Yiping.Mechanics of materials［M］.Sichuan：Sichuan University Press，2011.（in Chinese）

［7］刘刚，阎石林.齿轮扭转啮合刚度数值计算方法研究［J］.煤矿机械，2012，33（11）：34－35.LIU Gang，YAN Shilin.Research on numerical calculation method of gear torsional mesh［J］.Coal Mine Machinery，2012，33（11）：34－35.（in Chinese）

［8］王晓军，刘韶庆.基于啮合刚度的传动链转角误差研究［J］.机械工程与自动化，2012，171（2）：180－182.WANG Xiaojun，LIU Shaoqing.Study on transmission chain rotation error based on meshing stiffness［J］.Mechanical Engineering and Automation，2012，171（2）：180－182.（in Chinese）

［9］吴文光，朱如鹏.基于Workbench的斜齿轮固有特性分析［J］.机械传动，2010，34（4）：54－56.WU Wenguang，ZHU Rupeng.Analysis on natural vibration characteristics of helical gear based on workbench［J］.Journal of Mechanical Transmission，2010，34（4）：54－56.（in Chinese）

［10］赵葵，刘海岷，雷海胜，等.基于ansys workbench的蜗杆斜齿轮静力学仿真［J］.武汉工业学院学报，2012，31（1）：28－31.ZHAO Kui，LIU Haimin，LEI Haisheng，et al.The static mechanics simulation of worm－helical gear based on ansys workbench［J］.Journal of Wuhan Polytechnic University，2012，31（1）：28－31.（in Chinese）

［11］付昆昆，郑百林，石玉权.基于接触有限元法的齿轮多齿时变啮合刚度数值分析［J］.计算机辅助工程，2012，21（5）：65－68.FU Kunkun，ZHENG Bailin，SHI Yuquan.Numerical analysis of multi－tooth time－varying meshing stiffness of gear based on contact finite element method［J］.Computer Aided Engineering，2012，21（5）：65－68.（in Chinese）