基于平面二次曲线的非单视点全景相机标定方法

韩 笑，廖粤峰

(1.河南机电高等专科学校电气工程系，河南 新乡 453000;2.河南机电高等专科学校自动控制系，河南 新乡 453000)

0 引言

在计算机视觉研究中，很多情况下需要获取周围360°的全景图像。全景视觉系统就是为了应对这种需求逐步开始得到广泛研究的。全景成像系统是指成像视场大于半球，并主要由普通相机和全向反射镜组成的系统，也叫全景相机［1］。全景相机可以分为单视点全景相机和非单视点全景相机，一般全景相机是在单视点环境下标定的，但由于单视点约束条件较为苛刻，系统很难精确标定［2-3］。因此，本文从实际应用出发，研究非单视点相机标定方法。

近年来，国内外学者针对全景相机标定方法展开了大量的研究。Geyer 和Daniilidis 所提出的标定方法是仅使用图像中的3 条直线投影曲线就可恢复出抛物面折反射全景相机的内部参数［4］。Swaminathan等人在非单视点折反射成像系统中使用了一个简单参数化模型，通过这个模型分析了该成像系统的特征［5］。Perdigoto 与Araujo 提出了一种由一个轴对称的反射镜和一个中心位于镜像轴针孔摄像机的系统标定方法，其中有2 个标定参数用到了非线性优化方法［6］。张雷改进了球面统一成像模型［7］，引入畸变参数，提出了一种基于平行直线投影性质的单图标定方法。杨长江等人提出了一种基于平面二次曲线的摄像机标定方法［8］，该方法只需要摄像机在2 个或2个以上不同的方位摄取一个含有3 个或3 个以上同心二次曲线的平面模板的图像，摄像机和平面模板都可以自由移动，该方法在求解过程中不需要非线性迭代，可以直接获得解析解。

本文在文献［8］的基础上提出一种基于平面二次曲线计算非单视点折反射全景相机反射镜位置与姿态的标定方法。首先推导非单视点折反射全景相机光线投影方程及坐标变换关系，然后利用全景图像和反射镜背部平面模板上3 个同心二次曲线的对应关系，线性计算出反射镜和相机的相对位置与姿态。在标定过程中不需要非线性迭代，可直接获得反射镜位置与姿态参数的解析解。本文假设反射镜镜面参数、镜头畸变参数及相机内参数均已知。

1 折反射全景相机投影模型

1.1 单视点双曲面折反射全景相机投影模型

根据小孔成像原理，在三维空间中，当入射光线的延长线经过双曲面反射镜的一个焦点时，其反射光线必经过另一个焦点。当全景相机投影中心与双曲面反射镜外部焦点重合时，整个系统满足单视点要求［9-11］。如图1 所示，a、b 为双曲面反射镜长短轴。

图1 双曲面折反射全景相机示意图

此时，全景相机坐标系原点Oc与反射镜外部焦点重合。设反射镜坐标系原点Om与双曲面反射镜内部焦点重合，二次曲面反射镜的方程如式(1)所示。

但当相机镜头投影中心与双曲面反射镜外部焦点不重合时，就不满足单视点要求。为此，文献［12］提出了一种基于光学畸变校正的折反射全方位视觉系统单视点约束测定方法。该方法首先建立实际图像与理想图像之间的映射关系，从而得到满足单视点约束的理想透视模型;然后根据空间圆的透视投影特性，又可以通过反射镜上端面边缘图像估计出反射镜相对于相机的位置和姿态。从而可以检测出单视点约束条件。

1.2 非单视点双曲面折反射全景相机投影模型

非单视点双曲面折反射相机投影过程如图2 所示。

图2 非单视点折反射全景相机示意图

此时入射光线延长线不经过反射镜内部焦点Om。但根据小孔成像原理，反射光线必定经过相机投影中心，即全景相机坐标系原点Oc。则反射镜坐标系和全景相机坐标系之间的坐标变换关系如式(2)所示:

其中，P'c、P'm分别表示反射镜坐标系和全景相机坐标系点齐次坐标，Rc为旋转矩阵，Tc为平移矩阵。

相机坐标系原点Oc在反射镜坐标系下的坐标Ocm可表示为:

1)透视相机成像模型。

空间中的一点坐标M［X，Y，Z］T，图像上的二维点坐标m［u，v］T，相应的齐次坐标分别为M'［X，Y，Z，1］T与m'=［u，v，1］T。全景相机模型采用针孔模型［13］，二维图像点m 与三维空间点M 之间的映射关系如式(4)所示:

其中，s 为一非零尺度因子，R 为旋转矩阵，T 为平移矩阵，总称为相机外参矩阵。K 为相机内参矩阵，且其中，u0、v0为主点坐标，f1、f2为图像尺度因子，γ 为畸变因子［14-15］。

2)空间点向像平面投影计算方程。

如图2 所示，设Pm1［xm1，ym1，zm1］为反射镜坐标系下一空间点坐标，m'为其对应图像点齐次坐标，Pm2［xm2，ym2，zm2］为入射光线与反射镜交点。如式(3)所示，已知反射镜方程与Ocm坐标，则入射光线V，Pm2点处反射镜面法向量N 及反射光线向量F 可用式(6)～式(8)表示:

因为反射角等于入射角，所以V、N、F 三个向量共面，则有式(9)所示方程组:

可以看出式(9)为非线性方程组，在已知Pm1，Ocm点坐标的情况下，无法给出Pm2点坐标的解析解。在实际求解过程中可根据式(6)～式(9)用非线性方法求出Pm2点坐标的数值解。设P'm2表示Pm2点齐次坐标，则根据式(2)和式(4)，图像点齐次坐标m'可表示为:

其中，s 为一任意非零尺度因子。

3)由图像点计算空间入射光线向量方程。

如图2 所示，已知图像点齐次坐标m'，则反射光线向量F 为:

其中，F 在世界坐标系下的向量坐标为［Fx，Fy，Fz］，Fc为反射光线F 在相机坐标系下向量坐标［16］。

则反射光线与反射镜交点Pm2坐标可表示为:

其中，系数k 及其参数可用式(14)～式(17)计算:

由式(12)可获得2 组解，Pm2点处法向量可由式(7)得到。由图2 反射光线F 与法向量N 关系可知:

式(18)可表示2 向量内积，满足式(18)的解即为需要的解。已知法向量N 及反射向量F，空间入射光线向量V 如式(19)所示:

2 反射镜位置与姿态计算

2.1 模板平面与图像平面之间的映射关系

假设模板平面位于世界坐标系的X-Y 平面上，即Z=0。设旋转矩阵R 的第i 列为ri，由式(2)可得:

仍用M 表示模板平面上点，但此时M=［X，Y］T，M'=［X，Y，1］T，这样模板平面上点M 与对应图像点m 之间映射关系为:

H 为一个3 ×3 矩阵，λ 为一常数因子，平移向量T 表示平面模板坐标系原点到相机坐标系原点的矢量。

2.2 反射镜位置姿态计算

图3 平面二次曲线模板与反射镜位置示意图

如图3 所示，同心二次曲线位于反射镜背部模板平面上，二次曲线中心为模板平面原点，模板坐标系Z 轴与反射镜轴线重合，与反射镜坐标系之间的关系可表示为:其中，Pm为反射镜坐标系下坐标，M'为模板平面坐标系下齐坐标，I 为单位矩阵，平移向量Td=［0，0，l］表示平面模板坐标系原点到反射镜坐标系原点的矢量，l 为反射镜背面到其内部焦点的距离。

假设模板平面二次曲线用矩阵C 表示，它在图像上的投影仍为二次曲线，用矩阵Q 表示，可以分别表示为:

记Q'=KTQK，如果令det(C)=det(Q')，det(H)=1，则由式(27)可得式(28):

假设用来标定的二次曲线为椭圆和圆，其中一个二次曲线矩阵为

由式(28)有:

将H=［h1，h2，h3］代入式(29)，可得:

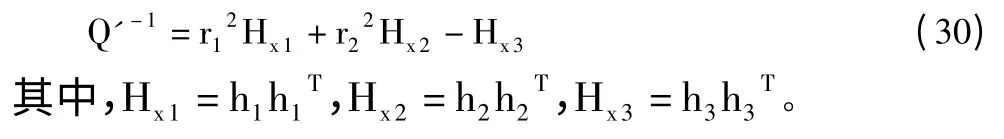
由于Hx1、Hx2、Hx3为未知变量，则至少需要3 个同心二次曲线才可以求解出Hx1，Hx2，Hx3。理论上，可将这3 个矩阵对角线上元素的平方根分别作h1，h2，h3各个分量的绝对值，符号由Hx1，Hx2，Hx3三个矩阵的上三角元素确定。但这种方法没有考虑噪声的影响及Hx1，Hx2，Hx3的奇异性。所以本文采用文献［8］提出的矩阵分解方法来确定h1，h2，h3。以h1为例，Hx1=h1h1T是秩为1 的对称矩阵，因此存在奇异值分解Hx1=UΛUT，U 为正交阵，由于噪声影响，一般计算出来的σ'i(i ＞1)并不等于0，但和σ'1相比非常小可以忽略，这样可以得到:

令:

可以求出h1=［g11，g12，g13］T。同样可以得到h2和h3。由式(22)可以看出，h1，h2，h3和r1，r2，Tc之间差一个比例系数λ。由于‖r1‖=‖r2‖=1，因此，可以计算出比例系数λ，如式(32)所示:

将式(32)代入式(22)可得r1=h1/λ，r2=h2/λ，T=h3/λ，此时式(20)中R 的第三个列向量可表示为r3=r1×r2。

联立式(10)、式(21)和式(23)，可以计算出反射镜坐标系相对于相机坐标系的旋转矩阵和平移向量为Rc=R，Tc=T-RTd。

3 全景相机标定实验

本文采用实拍图像实验来检验提出的标定算法。其中反射镜镜面参数为a=31.2888 mm，b=51.1958 mm，反射镜半径r=40 mm，计算得l=23.0941 mm。实验环境如图4 所示。

图4 非单视点实验环境示意图

相机分辨率为1024 ×768。用相机拍摄20 幅标定板图像，采用MATLAB 标定工具箱标定出相机内参数及镜头畸变参数，如表1 所示。

表1 相机标定结果

反射镜背面模板平面上的同心二次曲线已专门制作，如图5 所示。

图5 标定使用的平面二次曲线示意图

2 个同心圆和一个椭圆，小圆是椭圆的内切圆，大圆是椭圆的外切圆。其中r1=47 mm，r2=55 mm。拍摄的全景图像如图6 所示。

图6 拍摄的非单视点全景图

对全景图像中同心二次曲线进行椭圆拟合，为消除镜头畸变带来的拟合误差，首先根据相机标定结果对全景图像进行畸变校正。椭圆提取结果如图7 所示。

图7 提取出的同心二次曲线图

计算出反射镜坐标系相对于相机坐标系的旋转矩阵和平移向量为:

使用文献［12］提出的方法，使用最内侧同心圆计算得到的平移向量结果为:

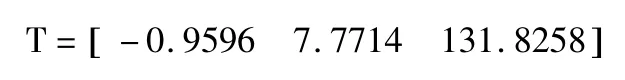
由上述可得，计算结果与本文所使用方法计算结果基本一致，由于文献［17］无法确定旋转矩阵R 的确切解，故不作比较。

对全景图像做柱面展开和透视展开，观察展开后的图像能否保持直线，同时与未标定的直接展开图做对比来评价标定结果，展开效果如图8 所示。

图8 全景图像柱面展开及透视展开图

如图8 所示，图8(a)与图8(c)为按单视点模型做透视和柱面展开的效果图。从图中可以看出全景图像中心发生了很明显的偏移，因此从展开图中可以发现立体标定块和平面标定块发生了很明显的扭曲，其中柱面展开图中扭曲更为明显;图8(b)与图8(d)为根据标定结果，用2.2 节的计算公式得到的透视和柱面展开图，通过对比可以发现立体标定块和平面标定块以及背景景物扭曲都已消除。因此，本文的标定结果是可信的。

4 结束语

本文提出了一种基于二次曲线的非单视点折反射全景相机标定方法，并给出了非单视点相机光线正反向投影计算方程。该方法原理简单，计算过程不需要非线性迭代，易于实现自动化，可实时计算反射镜位置与姿态，用于单视点约束测定或全景图像无畸变展开。接着本文根据提出的标定方法进行了相关的标定实验，用全景透视和柱面展开图像验证了标定结果。

［1］Puig L，Bermudez J，Sturm P，et al.A calibration of omnidirectional cameras in practice:A comparison of methods［J］.International Journal of Computer Vision，2012，11(6):120-137.

［2］陈铎.摄像机标定方法研究与实现［D］.沈阳:东北大学，2008.

［3］Ramalingam S，Sturm P，Lodha S K.Generic self-calibration of central cameras［J］.Computer Vision and Image Understanding，2010，114(2):210-219.

［4］Geyer C，Daniilidis K.Paracatadioptric camera calibration［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，2002，24(5):687-695.

［5］Swaminathan R，Grossberg M D，Nayar S K.Non-single viewpoint catadioptric cameras:Geometry and analysis［J］.International Journal of Computer Vision，2006，66(3):211-229.

［6］Perdigoto L，Araujo H.Calibration of mirror position and extrinsic parameters in axial non-central catadioptric systems［J］.Computer Vision and Image Understanding，2013，117(8):909-921.

［7］张雷.单视点折反射成像系统的建模、标定与应用［D］.杭州:浙江大学，2010.

［8］杨长江，孙凤梅，胡占义.基于平面二次曲线的相机标定［J］.计算机学报，2000，23(5):541-547.

［9］Micusik B.Two-view geometry of omnidirectional cameras［D］.Prague:Czech Technical University，2004.

［10］Scaramuzza D，Martinelli A，Siegwart R.A toolbox for easily calibrating omnidirectional cameras［C］// Proceedings of the 2006 IEEE/RSJ International Conference on Intelligent Robots and Systems.2006:5695-5701.

［11］Christopher Mei，Patrick Rives.Single viewpoint omnidirectional camera calibration from planar grids［C］// Proc.IEEE Int.Conf.Robot.Autom，2007:3945-3950.

［12］朱齐丹，张帆，李科，等.折反射全方位视觉系统单视点约束测定新方法［J］.华中科技大学学报(自然科学版)，2010，38(7):115-118.

［13］张铖伟，王彪，徐贵力.摄像机标定方法研究［J］.计算机技术与发展，2010(11):175-176.

［14］贾丹.摄像机现场标定算法研究［D］.哈尔滨:哈尔滨工程大学，2007.

［15］陈江.二目立体测量系统关键技术研究［D］.南京:南京航空航天大学，2006.

［16］Caglioti V，Taddei P，Boracchi G，et al.Single-image calibration of off-axis catadioptric cameras using lines［C］//Proceedings of the 11th IEEE International Conference on Computer Vision.2007:1-6.

［17］Mashita T，Iwai Y，Yachida M.Calibration method for misaligned catadioptric camera［J］.IEICE Transactions on Information and Systems，2006，89(7):1984-1993.