改进的模板匹配显微细胞图像分割算法

葛 亮，于 卡

(1.重庆大学计算机学院，重庆 400044;2.软件理论与技术重庆市重点实验室，重庆 400044)

0 引言

随着医学影像和信息技术的迅速发展，图像处理与计算机视觉技术被广泛应用于生物医学工程领域，极大推动了生物医学的发展。利用计算机技术对显微成像设备采集的数字细胞图像进行自动分析和处理，可以有效降低病理医师的劳动强度和工作量，避免人工操作中受主观因素的影响。因此，计算机图像处理技术在细胞图像处理领域中的应用研究逐渐成为世界范围内的热门课题［1］。

在此研究中，最基本和首要的任务是进行图像中细胞的分割，它是细胞体视学中量化分析与处理工作的重要基础。到目前为止，现有的图像分割算法都能够应用于细胞图像分割中，如阈值法、数学形态法、边缘检测法等。阈值法根据应用场合和分割目的不同，分为单阈值法和多阈值法。如果仅提取细胞核区域或细胞体区域，可使用单阈值法。Lin Zhonghua 首先对彩色细胞图像进行K-L 变换得到灰度图像，然后使用最大方差阈值选择(Otsu)法进行阈值判定，把细胞体区域和背景区域进行分离［2］。P.K.Sahoo 等使用二维Renyi 熵确定单阈值，对细胞图像进行分割［3］。若要同时提取细胞核区域和细胞质区域，可使用多阈值法。谢凤英等采用扩展Otsu 法获得双阈值，实现免疫细胞的细胞质与细胞核分割［4］。D.Bruzzese 等基于模糊熵理论求解多阈值实现从血细胞图像中分割红细胞区域［5］。阈值法的优点是速度快、计算简单，对目标和背景反差较大的细胞图像分割有效。但当背景复杂或目标与背景反差很小时，难以取得满意效果。数学形态学分割方法中有一种应用广泛的方法是基于拓扑理论提出的分水岭算法，K.Jiang 等将分水岭算法应用到三维HSV 颜色空间中，实现了血细胞图像中白细胞细胞核与细胞质的分割［6］。W.Chen 等根据形态学重构确定分水岭标记点，使用基于梯度图像的分水岭算法，从血细胞图像中分割细胞核和细胞质［7］。分水岭算法虽然能够在一些图像中取得较好的分割效果，但对绝大多数图像而言，分水岭法存在过分割的问题。换言之，分水岭方法依赖于标记的选取并且对噪声十分敏感。在边缘检测法中，检测图像目标边界通常使用边缘检测模板或边缘检测算子。赵英红等首先利用Canny 算子对胸水细胞边缘进行初次提取，然后利用数学形态学中的线形和菱形结构元素及填充函数对细胞边缘进行精确提取，该算法获得了较好的实验结果［8］。C.H.Lin 等先使用Sobel 算子对宫颈细胞图像进行边缘提取，而后引入非最值抑制策略按照梯度方向判断边缘点是否应该保留，经剪枝和细化后，选取最长的2 条封闭边缘作为细胞质和细胞核的边缘［9］。边缘检测算法一般只适用于边界较明显的细胞图像，对于边界模糊及灰度变化较复杂的图像，通常很难得到理想的分割结果。上述这些细胞图像分割算法，在一些光照均匀、背景简单或者只是存在单个细胞的图像中分割效果很好，但对于光照不均匀、背景复杂、边界模糊以及存在粘连细胞的图像中分割效果却不是很理想，所以研究更为智能更为普适的分割算法尤为重要。C.Chen提出了通过模板匹配来分割细胞图像［10］，该算法在显微细胞图像分割中具有很好的通用性。从实验结果可以看出，该算法所获得的细胞边界与实际情况比较吻合。对于光照不均匀及含有粘连的细胞图像，也能提取理想的细胞组织边界。它的缺点是在创建模板集时，过多地关注于尽可能多地产生模板，以至于产生了较多冗余模板，从而造成图像分割时间过长的问题。

本文针对C.Chen 所提出的传统模板匹配显微细胞图像分割算法在产生的模板集中存在冗余的问题，在深入分析产生冗余模板原因的基础上，提出了改进的模板匹配显微细胞图像分割算法。该算法通过精简模板集，达到了缩短图像分割时间，提高算法效率的目的。通过与现有细胞图像分割算法的对比，验证了改进算法的有效性。

1 传统模板匹配细胞图像分割算法

传统模板匹配细胞图像分割算法分为学习阶段和分割阶段。在学习阶段，为待分割细胞构建形状和亮度的统计模型，产生模板集。在分割阶段，利用模板集分割测试图像。图1 描述了该算法的一般流程。

图1 传统模板匹配细胞图像分割算法流程图

在学习阶段，首先需要获取细胞样本图像，该算法构建了一个简单的图形用户界面，通过在该界面中加载训练图像，手动在该图像中描绘矩形子窗口的方式得到样本图像，为了获得最佳结果，所选择的样本图像应尽可能包含不同类型和形状的细胞。接着对样本图像进行刚性配准［11］，采用了归一化互相关(Normalized Cross Correlation，NCC)作为优化准则，并且在优化过程中对样本图像进行旋转倒置(图像翻转)以得到最匹配的角度。之后使用这些处理过后的样本图像来评估标准模板［12］并且使用水平集方法［13］来分割标准模板，这个标准模板代表了所有样本图像的形状和亮度平均值。得到标准模板以后，使用主成分分析(Principal Component Analysis，PCA)技术建立统计模型，产生基本模板集。最后通过对基本模板集中的每幅图像在7 个方向(每次旋转30°)上进行旋转来扩大模板集，得到最终模板集。

在分割阶段，首先计算最终模板集中所有模板与测试图像区域的NCC 相似性，并把最大的相似性值作为像素点的检测值，得到检测图。接下来对检测图进行处理，得到细胞位置的种子点。对检测图处理的依据有2 个，一是检测图中的检测值应大于所设定的阈值;二是细胞间应相隔一定的距离。然后，利用种子点所对应模板的细胞形状把种子点所对应的细胞大致区域分割出来，得到测试图像的近似分割。最后，通过判断近似分割中的细胞是单个细胞还是粘连在一起的细胞，使用非刚性配准技术对细胞边界进行调整，得到测试图像的精确分割。

采用传统模板匹配细胞图像分割算法对显微细胞图像进行实验，所产生的基本模板集中的部分模板如图2 所示。从图中可以看出该模板集中存在许多相似度过高的冗余模板，直接影响分割阶段图像的分割速度。因此分析基本模板集的生成过程，找出产生冗余模板的原因进而精简模板集是非常必要的。从传统模板匹配算法过程可以看出，该算法使用PCA技术建立统计模型，产生基本模板集［10］，其算法过程为:1)将每幅样本图像分别与标准模板进行非刚性配准，记录图像中所有像素的空间变化情况，进而把所有样本图像中像素的空间变化情况组合得到空间变化矩阵v。2)使用PCA 技术，计算该空间变化矩阵的平均值和协方差矩阵，接着计算该协方差矩阵的特征值λp和特征向量qp(p=1，2，3，...)。3)通过保留大的特征值所对应的特征向量来构建统计模型，在这里，特征值选取的标准是特征值累计之和大于特征值总和的95%。统计模型的主要变化定义为=+bpqp，其中取bp=。4)根据vp，bp，由标准模板插值形变得到一组基本模板。从上述基本模板集的产生过程来看，特征值选取所设定的阈值为特征值累计之和大于特征值总和的95%，当选取的特征值比较小时，对特征值进行5 次取样的值bp相差不大，进而vp，bp的值相差会很小，用其对标准模板进行形变，所生成的模板集会存在相似度很高的冗余模板。其次，的值是由、bp和qp的值来确定，随着这3 个值的变化，会使得所计算出来的值非常接近，产生模板的冗余。从上述分析可以看出，有必要剔除基本模板集中的冗余模板，以提高算法效率。

图2 基本模板图像

2 改进的模板匹配细胞图像分割算法

精简传统模板匹配算法产生的模板集是本文算法的核心，其基本过程包括:提取模板的形状特征、度量模板间的相似度和剔除冗余模板，如图3 所示。在传统模板匹配图像分割算法中，模板中的细胞形状与测试图像中的细胞形状越相似，算法得到的分割结果就越好，同时测试图像中的细胞区域也是由其所对应模板的细胞形状分割出来的;此外，最终模板集是由基本模板集中的每个模板在7 个方向上旋转所得到的，删除一个基本模板相当于在最终模板集中删除其所对应的7 个不同方向的模板，可以通过精简基本模板集来达到精简最终模板集的目的。因此本文采用基本模板的形状特征作为分析冗余模板的依据。

图3 精简模板集的流程图

1)提取形状特征。

首先需要提取基本模板集中所有模板的形状特征。本文使用基于区域的形状描述法［14］，通过计算含有14 个分量的特征向量Fm=(Φ1，Φ2，Φ3，Φ4，Φ5，Φ6，Φ7，Area，Perimeter，MajorAxisLength，MinorAxisLength，Eccentricity，EquivDiameter，Solidity)来描述模板的形状特征。其中，m 表示模板的编号(m=1，...，N，N 为模板总数);Φi(i=1，...，7)是7 个Hu 不变矩，计算方法见公式(1);Area 表示区域面积，用图像中细胞区域的像素总数来度量;Perimeter 表示区域周长，用图像中细胞区域边界像素总数来度量;MajorAxisLength、MinorAxisLength 和Eccentricity 分别表示与细胞区域具有相同标准二阶中心矩的椭圆的长轴长度、短轴长度和离心率;EquivDiameter 表示与细胞区域具有相同面积的圆的直径;Solidity 表示细胞区域像素总数与其最小凸多边形中的像素总数的比值。上述特征都具有旋转不变性的特点。

2)度量相似性。

在使用特征向量Fm度量模板集中模板间相似性时，由于Fm各维的分布在数量级上差异很大，本文采用标准化欧氏距离来定义模板图像之间的相似性距离d(见公式(2))，并将此距离归一化(见公式(3))，从而得到对称的相似性矩阵。当模板总数为N 时，相似性矩阵的大小为N×N。

其中d 为模板a 与模板b 间的相似性距离，Fak表示模板a 的第k 个特征分量，Fbk表示模板b 的第k 个特征分量，sk表示第k 个特征分量的标准差。

其中D 表示模板间归一化相似性距离，dmax表示模板集中任意2 个模板间相似性距离的最大值。

3)剔除冗余模板。

设定相似性阈值tsimilar，剔除基本模板集中相似度过高的模板。即对步骤2)所得到相似性矩阵的下三角按照行进行扫描，当某矩阵元素的值大于或等于tsimilar时，剔除该矩阵元素所在列对应的模板，最终得到精简模板集。

3 实验及结果分析

本文在U2OS(包含48 张图像)和NIH3T3(包含49 张图像)2 个细胞图像集上进行实验。该细胞图像集［15］来自Dr.Murphy 实验室，是通过郝思特33342 荧光信号获得，并且在图像集中提供了由医学专家人工分割得到的标准分割结果。其中，U2OS 图像集中的细胞形状具有多样性，并且存在细胞粘连的情况;而NIH3T3 中的图像强度分布不均匀。

所有的实验在处理器为英特尔Xeon E5530，内存为8 G 的机器上运行。在实验中，本文算法的tsimilar设置为0.95(该值是根据经验法来确定，对于不同的细胞图像集，该值保持不变)，其他参数的设置与传统模板匹配算法［10］的参数设置保持不变。

本文对Otsu 阈值分割算法［16］、分水岭算法［17］、传统模板匹配算法和本文算法进行了对比实验。Otsu 阈值分割算法，是从灰度直方图中通过判定准则自动选择阈值来分割图像。对于分水岭算法，首先根据扩展的H-maxima 变换和H-minima 变换确定前景种子点和背景种子点，然后根据种子点找出区域边界分割图像。对于模板匹配算法，先把图像集分为训练图像和测试图像2 部分，通过在训练图像中选取样本图像产生基本模板集，并对每个基本模板在7 个方向上进行旋转(每次旋转30°)，得到最终模板集;然后利用最终模板集对测试图像进行分割，得到分割结果。其中，传统模板匹配算法从U2OS 图像集的训练图像中选取了35 张细胞样本图像，产生了60 个基本模板和420 个最终模板;从NIH3T3 图像集的训练图像中选取了40 张细胞样本图像，产生了70 个基本模板和490 个最终模板。而本文算法对传统算法产生的基本模板集提取形状特征，并计算其相似度，进而剔除相似度大于等于0.95 的模板来精简模板集。对于U2OS 图像集，精简得到41 个基本模板和287 个最终模板，模板集规模缩减31.7%;对于NIH3T3 图像集，得到42 个基本模板和294 个最终模板，模板集规模缩减40.0%。模板集精简前后对比如表1 所示。图4 和图5 展示了在U2OS 图像集和NIH3T3 图像集中部分相似度大于等于0.95 的模板，图4 和图5 中(b)部分图像的右上角用白色数字标注了其与(a)部分图像的相似度数值，在本文算法中，通过剔除(b)部分的图像来精简模板集。

表1 模板集缩减前后对比

图6～图7 展示了图像集中部分图像的分割结果。通过直观对比可以看出，Otsu 阈值分割算法在光照比较均匀的图像中，分割出来的细胞会存在许多孔洞以及细胞边界不光滑的现象;对于光照不均匀的情况，只能分割出少量亮度强的细胞。分水岭算法的分割结果存在过分割、误分割、不贴合细胞边界、不能很好地分割粘连细胞的现象。而本文算法和传统模板匹配算法都有较好的分割结果，同时本文算法的分割结果与传统模板匹配算法相比，几乎没有变化。

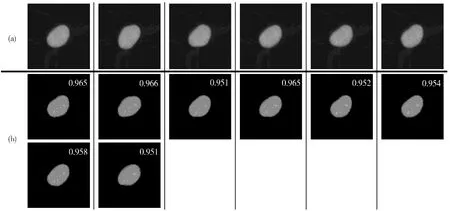
图4 U2OS 图像集中部分相似度过高的模板

图5 NIH3T3 图像集中部分相似度过高的模板

图6 不同分割算法在U2OS 图像集(均匀光照下)的分割结果对比

图7 不同分割算法在NIH3T3 图像集(不均匀光照下)的分割结果对比

表2 不同算法分割结果的定量比较

为了进一步验证本文算法的有效性，采用不同评价指标［15］对上述算法的实验结果做定量分析。定量分析的基本思想是将标准分割结果图像R 与算法分割结果图像S 进行比较，计算两者间的相似度指标或者差异度指标。本文计算的指标具体包括:

1)RI 值(Rand Indices)和JI 值(Jaccard Indices)。

RI 值和JI 值的定义如下:

假设i 和j 代表原图像中的像素(i≠j)，则i 和j组成的所有像素对被分为4 种类别:①Ri=Rj并且Si=Sj;②Ri≠Rj并且Si=Sj;③Ri=Rj并且Si≠Sj;(4)Ri≠Rj并且Si≠Sj。公式中a，b，c，d 对应于4 种类别中每一种类别的像素对个数。这2 个指标用于度量正确分割所占的比值，数值越大说明算法分割结果越接近标准分割结果。

2)距离归一化总和(Normalized Sum of Distances，NSD)和Hausdorff 距离(H)。

NSD 和H 的定义如下:

其中，i 表示R 图像中细胞像素与S 图像中细胞像素并集中的像素，D(i)表示像素i 与标准分割结果中细胞边界之间的距离。这2 个指标考虑了空间信息，弥补了RI 和JI 没有考虑空间特征信息的缺点，数值越小说明算法分割结果越接近标准分割结果。

3)细胞误分个数:Split，Merged，Added 和Missing。

Split 表示算法将标准分割结果中的一个细胞误分为2 个细胞的个数;Merged 表示算法将标准分割结果中的2 个细胞合并为一个细胞的个数;Added 表示算法将标准分割结果中的背景误分割为细胞的个数;Missing 表示算法将标准分割结果中的细胞误以为是背景的个数。细胞误分个数指标的数值越小，意味着分割结果越好。

把不同算法在U2OS 和NIH3T3 图像集上的分割结果分别与标准分割结果进行对比，计算上述评价指标，结果见表2。其中，黑色加粗数字代表每个指标的最佳值。从总体来看，虽然Otsu 阈值分割算法和分水岭算法平均分割每幅图像所需的时间非常少，但从图像分割的性能来看，远不及本文方法和传统模板匹配算法。对比本文算法和传统模板匹配算法，两者的分割质量评价指标值相当，说明模板集的缩减并没有对分割质量产生影响。同时，本文算法在图像分割运行时间上有了大幅度的减少。对于U2OS 和NIH3T3 图像集，算法平均运行时间分别缩短了35.0%和40.7%。

4 结束语

本文描述了一种改进的模板匹配显微细胞图像分割算法，该算法通过精简模板集来提高传统模板匹配显微细胞图像分割算法的效率。通过对2 个不同显微细胞图像集的实验，定量分析了新算法的性能，并与传统模板匹配分割算法、阈值分割算法和分水岭算法进行了比较。实验结果表明，本文算法和传统模板匹配分割算法在分割准确率方面远高于阈值分割算法和分水岭算法。同时，本文算法通过精简模板集，在保持分割质量的情况下，大幅度减少了平均分割每幅图像所需的时间，提高了算法的执行效率。下一步将考虑改进算法的模板匹配环节，提高算法对于背景复杂的细胞图像的分割准确率。

［1］李宽.细胞图像的分割、纹理提取及识别方法研究［D］.长沙:国防科学技术大学，2012.

［2］Lin Zhonghua.The cell image segmentation based on the K-L transform and Otsu method［C］// Proceedings of the International Conference on Multimedia and Signal Processing.2011:25-28.

［3］Sahoo P K，Arora G.A thresholding method based on twodimensional Renyi's entropy［J］.Pattern Recognition，2004，37(6):1149-1161.

［4］谢凤英，姜志国.基于最大方差的免疫细胞图像双阈值分割［J］.中国体视学与图像分析，2007，12(1):59-61.

［5］Brussese D，Giani U.Automatic multilevel thresholding based on a fuzzy entropy measure［M］// Classification and Multivariate Analysis for Complex Data Structures.2011:125-133.

［6］Jiang Kan，Liao Qing-min，Xiong Yuan.A novel white blood cell segmentation scheme based on feature space clustering［J］.Soft Computing，2006，10(1):12-19.

［7］Chen Wei-bin，Zhang Xin.A new watershed algorithm for cellular image segmentation based on mathematical morphology［C］// Proc.of the 2010 International Conference on Machine Vision and Human-Machine Interface(MVHI).2010:653-656.

［8］赵英红，乔双，董丽华.Canny 算子与数学形态学算子相结合实现胸水细胞的边缘提取［J］.东北师大学报(自然科学版)，2008，40(3):42-45.

［9］Lin Chuen-horng，Chan Yung-kuan，Chen Chun-chieh.Detection and segmentation of cervical cell cytoplast and nucleus［J］.International Journal of Imaging Systems and Technology，2009，19(3):260-270.

［10］Chen Cheng，Wang Wei，Ozolek J A，et al.A flexible and robust approach for segmenting cell nuclei from 2D microscopy images using supervised learning and template matching［J］.Cytometry A，2013，83(5):495-507.

［11］Rohde G K，Ribeiro A J，Dahl K N，et al.Deformation-based nuclear morphometry:Capturing nuclear shape variation in hela cells［J］.Cytometry A，2008，73(4):341-350.

［12］Heitz G，Rohlfing T，Maurer C R.Statistical shape model generation using nonrigid deformation of a template mesh［C］// Proceddings of SPIE Medical Imaging.2005:1411-1421.

［13］Li Chun-ming，Xu Chen-yang，Gui Chang-feng，et al.Level set evolution without reinitialization:A new variational formulation［C］// Proceedings of IEEE Conference on Computer Vision and Pattern Recognition(CVPR).2005:430-436.

［14］冈萨雷斯.数字图像处理(MATLAB 版)［M］.阮秋琦，译.2 版.北京:电子工业出版社，2007:321-363.

［15］Coelho L P，Shariff A，Murphy R F.Nuclear segmentation in microscope cell images:A hand-segmented dataset and comparison of algorithms［C］// Proceedings of the 9th IEEE International Symposium on Biomedical Imaging.2009:518-521.

［16］Otsu N.A threshold selection method from gray-level histograms［J］.IEEE Transactions on Systems，Man and Cybernetics，1979，9(1):62-66.

［17］Wahlby C，Sintorn I，Erlandsson F，et al.Combining intensity，edge and shape information for 2D and 3D segmentation of cell nuclei in tissue sections［J］.Journal of Microscopy，2004，215(Pt1):67-76.