一种改进型的分布式Lazy 关联分类算法

杨浩敏，马 超，吴海燕

(重庆大学计算机学院，重庆 400044)

0引言

关联分类算法［1］是基于关联规则的分类算法。相对于决策树算法、贝叶斯算法、KMeans 算法以及支持向量机等分类算法，关联分类算法在准确率和可拓展性方面有着不错的表现，成为分类算法研究领域重要的分支。关联分类算法总体上可以分为2 大类:显式关联分类算法和lazy 关联分类算法［2］。

显式关联分类算法的训练和分类这2 个环节是彼此独立的，在国际上比较有影响力的算法主要有CBA［3］算法和CMAR［4］算法。

Lazy 关联分类算法将训练阶段推迟到了分类阶段，典型算法是Veloso A 等人于2006 年提出的。该算法先将待分类样本对训练样本做投影操作，然后利用挖掘出来的关联规则构建分类器，能够较好地解决显式关联分类算法存在的small disjunction 和候选规则集过大的问题。Elena Baralis 等人在2008 年提出采用lazy 思想进行剪枝的L3算法［5］，严格意义属于显式关联分类。2013 年，付萌等人利用混合策略方法［6］，将lazy 方法的优点应用到显式关联分类中;李宾飞等人则将lazy 方法应用到数量型关联分类中［7］。在lazy 关联分类算法中，每个待分类样本都要对训练样本进行投影并构建一个分类器，对多个待分类样本进行分类时效率很低。

分布式关联规则挖掘算法能够提升lazy 关联分类关联规则挖掘环节的效率，典型算法是基于Apriori的并行算法［8］。D.W.Cheung 于1996 年提出了FDM算法［9］，利用局部剪枝基于Apriori 的并行算法进行改进，减少各个分区间的数据通讯量。王越在2003年提出了带有中心节点的C-DMA(Center-Data Mining Algorithim)算法［10］，将全局剪枝放到中心节点中进行，将数据通讯局限在中心节点和各个分节点之间。张春生等人利用数据局部性对C-DMA 算法进行改进［11］，提出分段支持度，使得分片之间几乎不用进行数据交换，不仅提高了算法的执行效率，也提高了算法挖掘全局规则的能力。针对lazy 关联分类算法特有的投影操作，并未见分布式实现。

应用分布式关联规则挖掘算法的lazy 关联分类算法称为分布式lazy 关联分类(DLAC)算法。现有的DLAC 算法存在2 个主要问题:1)对多个待样本进行分类时效率低下;2)投影操作未分布式实现。第一个问题是lazy 关联分类本身的问题，第二个问题是分布式关联规则挖掘算法应用于lazy 关联分类所带来的问题。针对上述2 个问题，本文提出一种改进型的分布式lazy 关联分类PDLAC 算法，对满足条件的多个待分类样本进行聚合，然后进行分布式投影并分布式地挖掘关联规则，最后构建分类器。对满足条件的多个待分类样本进行聚合，有效地解决lazy 关联分类算法对多个待分类样本进行分类的效率问题;分布式投影解决了分布式关联规则挖掘算法应用于lazy关联分类时的不足。

1 分布式lazy 关联分类算法

DLAC 算法主要由2 部分组成:lazy 关联分类算法和分布式关联规则挖掘算法C-DMA。

1.1 Lazy 关联分类算法

lazy 关联分类算法是在显式关联分类算法的基础上发展而来的。

典型的显式关联分类算法是CBA 算法，算法步骤如下:

1)离散化训练样本和待样本中的连续属性。

2)使用关联规则挖掘算法Apriori，挖掘出候选的关联规则CARs。

3)使用分类器构造算法CBA-CB，从候选的关联规则CARs 中选择合适的关联规则来构建分类器。

关联分类中涉及的基本概念:

假 设 T={t1，t2，...，tn}为事务集，Ti={t1i，t2i，...，tni}为一个事务，t1i，t2i，...，tni称为Ti的子项，Ti的子集称为项集S，S⊆Ti。设项集A、B，那么关联规则定义为“A→B”。在关联分类当中，A 一般为属性的集合，B 一般为类别。

关联规则A→B 可用如下参数描述:

支持度:

置信度:

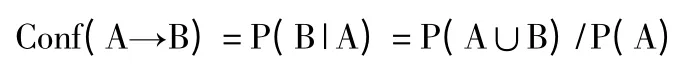
步骤2)中使用关联规则挖掘算法Apriori 挖掘出支持度较高的关联规则。步骤3)中优先选择CARs中置信度高的关联规则插入分类器，并删除该关联规则覆盖的训练样本对象，如果该关联规则没有覆盖任何训练样本对象，则不加入分类器当中。对于训练样本中不被CARs 关联规则覆盖的样本对象，选择大部分样本所属类别作为默认类。

lazy 关联分类算法对每一个待分类样本构建一个分类器。算法步骤如下:

1)每一个待分类样本对训练样本进行投影。

2)在投影后的训练样本中，使用关联规则挖掘算法挖掘支持度较高的关联规则。

3)选择置信度最好的一条关联规则，对待分类样本进行分类。

1.2 分布式关联规则挖掘算法

C-DMA 算法是由FDM 算法发展而来的，是对并行Apriori 算法的一种改进，算法的具体步骤如下，其算法流程图如图1 所示。

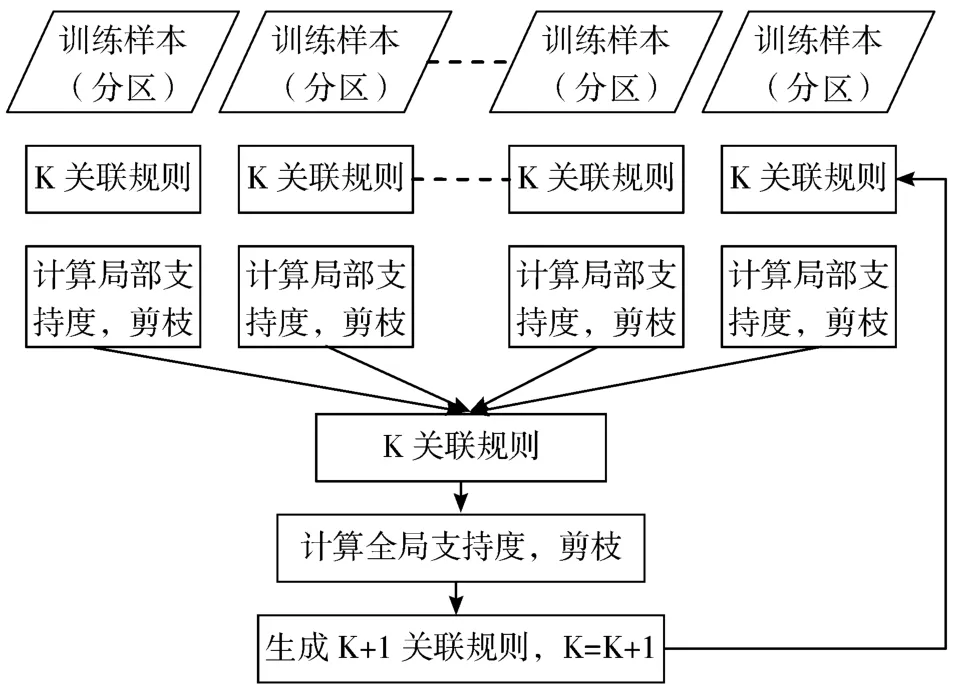
图1 C-DMA 算法流程图

1)将训练样本分区，K=1。

2)在各个分区中挖掘K 候选关联规则，根据局部支持度，对候选关联规则进行裁剪。

3)汇总各个分区的候选关联规则，根据全局支持度，对候选关联规则进行剪枝。

4)根据剪枝后的K 候选关联规则，生成K+1 候选关联规则，K=K+1。

5)循环步骤2)～4)，直到无法生成候选关联规则。

1.3 DLAC 算法存在的问题

显式关联分类算法直接从训练样本中挖掘关联规则，构建分类器，多个待分类样本使用同一个分类器。lazy 关联分类算法采用lazy 分类思想［12］，每一个待分类样本先对训练样本做投影，然后挖掘关联规则构建分类器，每一个待分类样本都对应一个分类器。经过研究，lazy 关联分类能够较好地解决显式关联分类算法存在的small disjunction 和候选规则集过大的问题，但也存在以下2 个缺点:

1)对多个待分类样本进行分类时，效率很低。

2)分类器中只有一条规则，容易导致过度拟合的问题。

分布式关联规则挖掘算法C-DMA 应用于lazy 关联分类中的时候，只在关联规则挖掘一个环节做了分布式实现，投影操作并没有分布式实现。

2 改进型的分布式lazy 关联分类算法

2.1 PDLAC 算法概述

基于上面的分析，本文提出改进型的分布式lazy关联分类PDLAC 算法。PDLAC 算法对待分类样本进行KMeans 聚类;其次，判断类内的待分类样本是否满足聚合条件，满足进行聚合，不满足则类内的每个待分类样本单独成为一类;然后，进行分布式投影并使用C-DMA 算法挖掘关联规则;最后，构建分类器对类内的一个或多个待分类样本进行分类。算法主要解决以下3 个问题:1)如何对待分类样本进行聚合;2)如何分布式实现投影操作;3)分类器如何构造。

基于lazy 方法的分布式关联分类算法模型如图2 所示。其算法步骤如下:

1)对待分类样本进行KMeans 聚类。

2)对每一个类别判断是否满足聚合条件，满足则进行聚合，不满足则每个待分类样本单独成为一类。

3)每一个待分类样本聚合对训练样本进行分布式投影操作。

4)使用C-DMA 算法挖掘关联规则。

5)对每一类待分类样本构建一个分类器。

6)使用分类器对类内的样本进行分类。

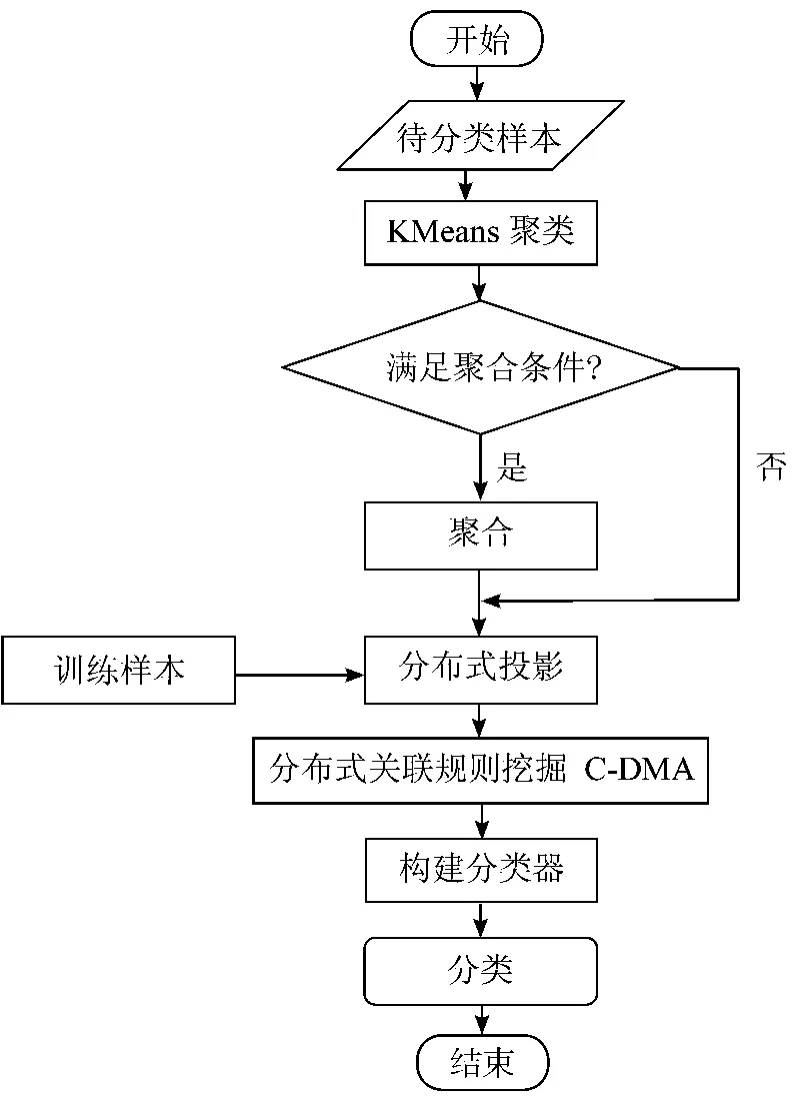
图2 PDLAC 算法流程图

2.2 待分类样本聚合

对待分类样本进行聚合，使得多个相似的待分类样本只需进行一次投影操作和关联规则挖掘。具体做法是使用KMeans 算法对待分类样本进行聚类，判断类别是否符合聚合条件，如果符合聚合条件则进行聚合，进行属性聚合，并进行分布式投影和关联规则分布式挖掘，最后构建该类别的分类器并进行分类;如果不符合聚合条件，每个待分类样本直接进行分布式投影并分布式挖掘关联分类规则，选取置信度最高的规则对待分类样本进行分类。对待分类样本进行聚合，需要解决2 个关键问题:KMeans 聚类的粒度问题，聚合判断条件。

KMeans 聚类的时候，聚类的类别个数与粒度成反比关系。确定了类别的个数就确定了聚类的粒度。假设训练样本每个维度的可选项个数为c，如果不同维度的可选项个数不同则取平均值，待分类样本个数为N，那么聚类的类别个数KMeans_ClassNum=3N/c。

待分类样本经过KMeans 聚类，形成多个类别，对每个类别中的待分类样本的属性进行聚合。I1，I2，...，In表示某个类别的待分类样本，I 表示样本聚合的结果，I=I1∪I2∪...∪In。LenI 表示聚合后I 的长度，LenIn表示I1，I2，...，In的平均长度，LenIn=LenIi/n。

聚合判断条件是ln LenI/ln LenIn＜ln n。

2.3 分布式投影

分布式投影将待分类样本或样本聚合的结果分发到各个训练样本分片中去，在各个分片中进行独立的投影操作，示意图如图3 所示。

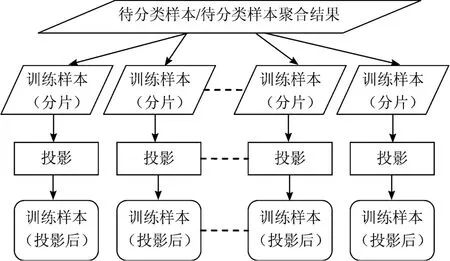
图3分布式投影示意图

2.4 分类器构造

分类器表示为R，C-DMA 算法生成的关联规则表示为CARs，CARs 中的一条关联规则表示为r，某个聚类的待分类样本表示为S。分类器构造的基本思想是挑选r 中优先级较高的规则，使之能够完整覆盖S。最终形成的分类器形如:

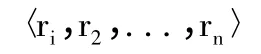
其中，〈ri，r2，...，rn〉左边的优先级高于右边，且分类器中不存在缺省类。

若规则ri和rj满足以下任一条件，则ri的优先级高于rj，记为ri＞rj。

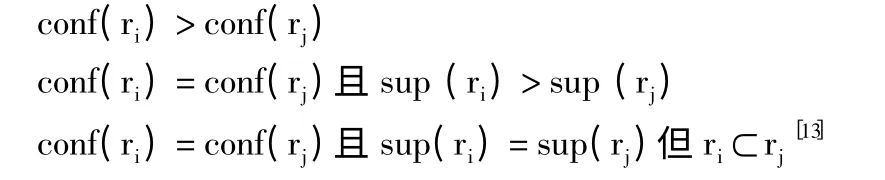
分类器构造的步骤如下:

1)按照优先级对关联规则进行排序。

2)依次挑选CARs 中的关联规则加入R 中。根据关联规则优先级高低，用每条关联规则检测待分类样本S，删除S 中被r 覆盖的样本，如果r 能够覆盖至少一个待分类样本，则将r 加入到R 中。

3)当CARs 中规则遍历完或不再有待分类样本时，结束规则选择过程。

3 实验与对比分析

3.1 实验环境

1)硬件环境。

实验的计算服务器使用曙光TC4600 刀片服务器，每台刀片的CPU 为16 核，内存32 G，存储为SAS硬盘300 G;交换机使用SummitX460-48t-10G 千兆交换机，背板带宽320 Gpbs。

2)分布式环境。

分布式环境使用Spark 1.0.1，部署模式为Standalone 模式，1 个Master 节点，3 个Worker 节点，见表1。Worker 节点上部署HDFS，用于存放数据。Worker 节点都可以用于分布式计算，并行最小粒度为1 CPU，所以该环境支持最高的并行度为36。

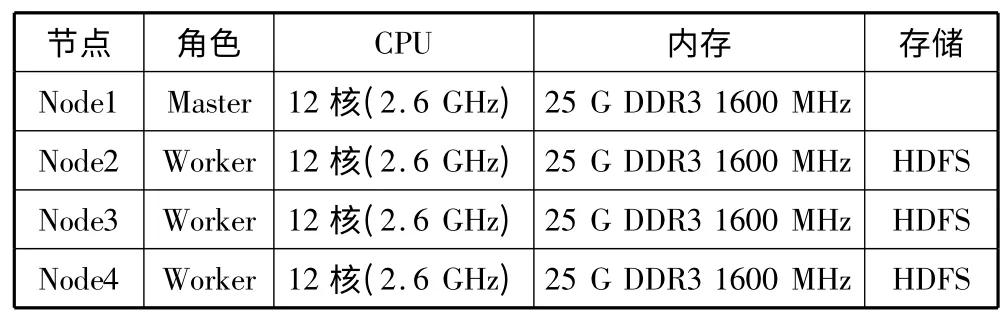
表1 分布式环境

3.2 实验数据

为了测试本文提出的基于lazy 方法的分布式关联分类算法的性能，本文选用第一届全国高校云计算创新应用大赛K-频繁项集挖掘并行算法使用数据集，用于本文算法时，随机给数据添加类别标识。由于本文提出的算法主要在提升算法效率，所以添加标识的做法并不会影响实验结果的可信度。由于实验数据在HDFS 中的分片数目为15，所以本文的实验的并行度为15。实验数据表如表2 所示。

表2 实验数据

3.3 结果与分析

为了验证分布式投影对算法性能的提升，在不同minSup 下，从数据集中任意抽取5 条待分类规则，对分布式投影的DLAC 算法与传统DLAC 算法的性能比较。同一支持度下的算法耗时为5 次耗时的平均值。算法设定的minConf 为60%。实验结果如图4所示。

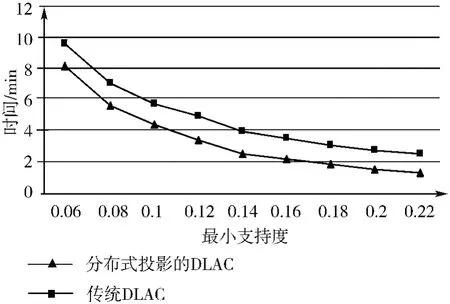
图4 分布投影的DLAC 与传统DLAC 性能比较

为了验证待分类样本聚合对算法性能的提升，本文对比了不同待分类样本数量下使用聚合方法的DLAC 算法与传统DLAC 算法的性能。算法设定的minSup 为20%，minConf 为60%。实验结果如图5所示。

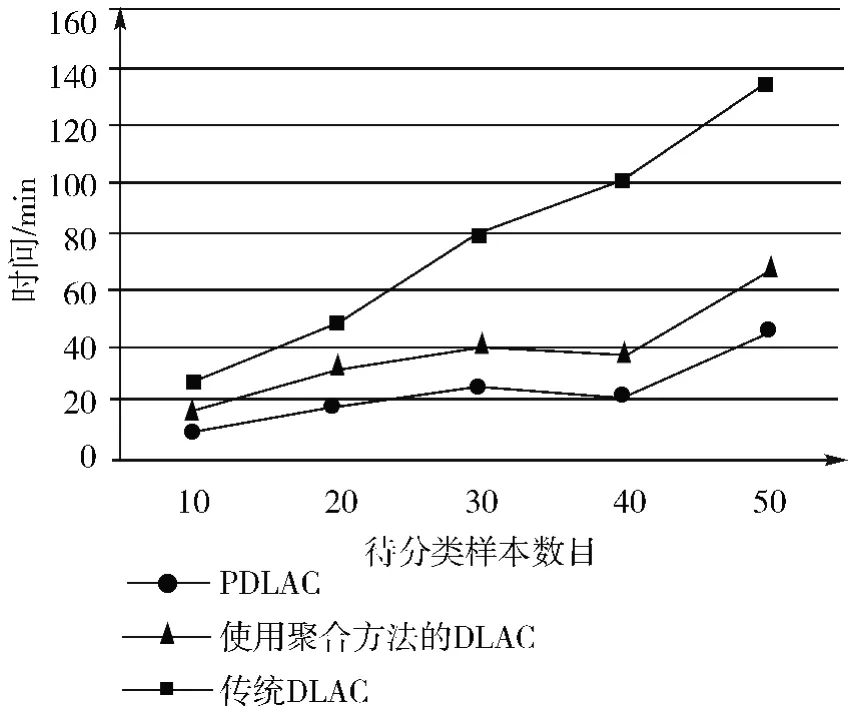
图5 PDLAC、使用聚合方法的DLAC 与传统DLAC 性能比较

从图4 中可以看出，在不同的minSup 下，使用分布式投影能够很好地提升DLAC 算法的性能，但性能提升的幅度随着minSup 的减小而递减。分布式投影能够提升性能主要是因为分布式投影相比串行投影有着性能的提升。性能提升幅度递减是因为投影操作只进行一次，而随着最小支持度的减少，候选规则集会非线性增大，分布式投影的性能提升对比候选规则集挖掘的时间比重越来越低。

从图5 中可以看出，使用聚合方法的DLAC 算法的性能远高于传统的DLAC 算法，主要是因为聚合使得满足条件的待分类样本使用同一个分类器，大大减少了对每个待分类构建一个分类器的时间。PDLAC算法所用的时间远小于DLAC 算法，因为PDLAC 算法集合了分布式投影与聚合方法的优点。随着待分类样本数目的增加，PDLAC 算法性能提升越大，因为待分类样本越多，能够使用同一分类器进行的分类的待分类样本越多，相比对每个待分类样本构建一个分类器，时间节省越多。

图4、图5 的结果表明本文提出的算法——PDLAC 算法更加优越，不仅解决了分布式关联规则挖掘算法应用于lazy 关联分类时的不足，也解决了lazy 关联分类本身存在的对多个待分类样本分类时效率低的问题。

4 结束语

本文提出了一种改进型的分布式lazy 关联分类PDLAC 算法，使用聚合方法与分布式投影改进传统的DLAC 算法。实验结果分析表明，PDLAC 算法相比传统的DLAC 算法，性能有着较大幅度的提升。对满足条件的多个待分类样本进行聚合，有效地解决lazy 关联分类算法对多个待分类样本进行分类的效率问题;分布式投影解决了分布式关联规则挖掘算法应用于lazy 关联分类时的不足。

下一步的工作是继续研究PDLAC 算法在待分类样本没有显著关联情况下的性能，并进一步改进算法使之适合待分类样本没有显著关联的情况。

［1］Thabtah F.A review of associative classification mining［J］.The Knowledge Engineering Review，2007，22(1):37-65.

［2］Veloso A，Meira W，Zaki M J.Lazy association classification［C］// Proc.of the 6th IEEE International Conference on Data Mining.2006:645-654.

［3］Liu Bing，Hsu W，Ma Yiming.Integrating classification and association rule mining［C］// Proc.of the 4th International Conference on Knowledge Discovery and Data Mining.1998:80-86.

［4］Li Wenmin，Han Jiawei，Pei Jian.CMAR:Accurate and efficient classification based on multiple class-association rules［C］// Proc.of IEEE International Conference on Data Mining.2001:369-376.

［5］Baralis E，Chuusano S，Garza P.A lazy approach to associative classification［J］.IEEE Transactions on Knowledge and Data Engineering，2008，20(2):156-171.

［6］李学明，付萌，李宾飞.基于混合策略的关联分类方法［J］.计算机应用，2013，30(3):724-727.

［7］李学明，李宾飞，杨涛，等.基于lazy 方法的数量型关联分类［J］.计算机应用，2013，33(8):2184-2187.

［8］Symth P，Goodman R M.An information theoretic approach to rule induction from databases［J］.IEEE Transaction on Knowledge and Data Engineering，1992，4(4):301-316.

［9］Cheung D W，Ng V T，Fu A W.Efficient mining of association rules in distributed database［J］.IEEE Transactions on Knowledge and Data Engineering，1996，8(6):911-922.

［10］王越.分布式关联规则挖掘的方法研究［D］.重庆:重庆大学，2003:17-18.

［11］张春生，李艳，庄丽艳，等.基于局部性原理的分布式关联规则挖掘算法［J］.计算机工程与应用，2012，48(21):143-145.

［12］Friedman J，Kohavi R，Yun Y.Lazy decision trees［C］//Proc.of the 13rd National Conference on Art Intelligence.1996:717-724.

［13］Wang Ke，Zhou Senqiang，He Yu.Growing decision trees on support-less association rules［C］// Proc.of the 6th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining.2000:265-269.