基于概率因果模型的核动力系统故障诊断

左绍义 廖磊 蔡琦 袁灿

摘 要：提出了一种将智能优化算法融入概率因果模型中实现核动力系统故障诊断的方法。根据概率因果模型，将一个核动力系统的故障诊断问题转化为寻优问题，然后将概率因果模型的极大似然估计作为入侵性野草算法的寻优条件，利用故障与征兆之间的关联强度实现故障诊断。实验结果表明，该方法具有较好的准确性和鲁棒性，能够满足实际故障诊断的需求。

关键词：故障诊断 入侵性野草算法 仿真计算

中图分类号：TL383 文献标识码：A 文章编号：1674-098X（2015）09（b）-0106-02

对核动力系统进行故障诊断目前来说，主要是通过现象或者征兆、可用的历史信息或者先验知识以及故障原因等来进行[1-4]，因此，可以将一个故障诊断问题形式化描述为：D=（F，S，I，S+），其中F={f1，f2，，fn}为故障的有限非空集，n表示所有故障的个数，S={s1，s2，，sm}为系统状态的有限非空集，m表示所有可能状态的个数，I为已知的先验信息，S+S为系统表征的现象或者征兆。

根据上述形式化描述，那么对于一些已知故障现象或者征兆的故障，可以利用概率因果模型，将故障诊断问题转化为给定征兆，求诊断假设的极大似然估计问题，通过寻找满足条件的最优方案，求得所属的故障类别。该类方法主要是用于处理已知故障集F与系统征兆集S之间的因果强度，而需要通过表征的现象或者征兆S+确定具体的故障分类问题，使用过程中通常与智能优化算法（包括遗传算法、粒子群算法、蚁群算法以及入侵性野草算法等）相结合。文中以入侵性野草算法为基础进行故障诊断，实验表明，该方法能够较好地处理已知故障现象或者征兆，判定故障类型的问题。

1 概率因果模型

经典概率因果模型有如下3个方面的假设[5-7]。

（1）假设故障与故障之间没有关联，即存在独立性。

（2）假设故障与原因之间的因果强度保持不变，一旦发生同一类型的故障，则相同的征兆会以同等的几率出现，即存在因果强度不变性。

（3）假设全部的征兆都是由故障引起的，没有故障发生就不会出现征兆，即存在征兆与故障的因果必然性。

则根据上述假设，可以将核动力系统故障诊断问题用下式来描述：

P=（F，S，C，S+） （1）

式中，

F为有限的故障集合，且恒不为空，若该集合存在i个故障，则F可表示为F={f1，f2，，fi}。

S为有限的征兆集合，且恒不为空，若该集合存在j个故障，则S可表示为S={s1，s2，，sj}。

C为征兆和故障之间的因果强度，且CD×M，Cmn为故障fm会引起征兆sn的概率。

S+为已知的征兆集合，则S+S；S—=S—S+表示已知不存在的征兆。

假设某故障集合FaF是诊断问题的解，即Fa中的元素全部都会发生，而非Fa中的元素都不会发生，那么对于这种类型的诊断问题，就可以将其转化为已知S+，求Fa的极大似然估计值：

（2）

上式中，对于给定的S+，为常数项，可以从函数中消除，则式（2）可以简化为：

）

（3）

由式（3）可知，在给定S+的情况下，可以进行任何Fa的极大似然估计值的计算，该值的大小反映了Fa在S+下发生的概率。

2 基于入侵性野草算法的概率因果模型诊断方法

2.1 入侵性野草算法

入侵性野草算法[8]（Invasive Weed Optimization，IWO）是近年来刚提出的一类种群优化算法，具有较好的适应性和鲁棒性，因而得到广泛应用。

IWO算法的基本过程如图1所示。

（1）根据故障诊断的实际问题，设定初始化参数，并产生随机的初始解。

（2）种群中的所有个体均能通过其自身、种群最小以及种群最大适应度函数值来获得下一代种子数目，式（4）为种子数目的计算公式。

（4）

式中、分别表示当前种群中最大适应度函数值和最小适应度函数值，、分别表示可生成种子数的最大值、最小值；floor（）函数表示向下取整。

（3）步骤2中产生的下一代种子随机地在空间中分布，下一代种子的值由其父辈加上随机数S来获得。S在空间中服从正太分布，且该正太分布的均值为0，标准方差为sig_cur。其中，sig_cur的计算方法如式5所示。

（5）

式中iter表示当前迭代次数，iter_max表示最大迭代次数，sig_ini和sig_final分别表示种子散布的初始步长和最终步长。

（4）若产生的种群总体上没有达到最大规模，则重复进行步骤2和步骤3，直至满足条件为止。然后对所有种子的适应度函数值进行排序，选取其值较大者作为下一次繁殖的父辈，较小者则被淘汰。

2.2 故障诊断方法

利用上述概率因果模型，可以将故障诊断问题转化为已知S+，求最大的问题。由于故障和非故障之间是不存在关联的，而大多数情况下故障又多种多样，可能会出现组合爆炸现象，因此需要采用入侵性野草算法来解决。

将模型中的式（3）作为IWO算法的适应度函数，结合第2.1节所述，其具体的诊断过程如图2。

3 仿真实验

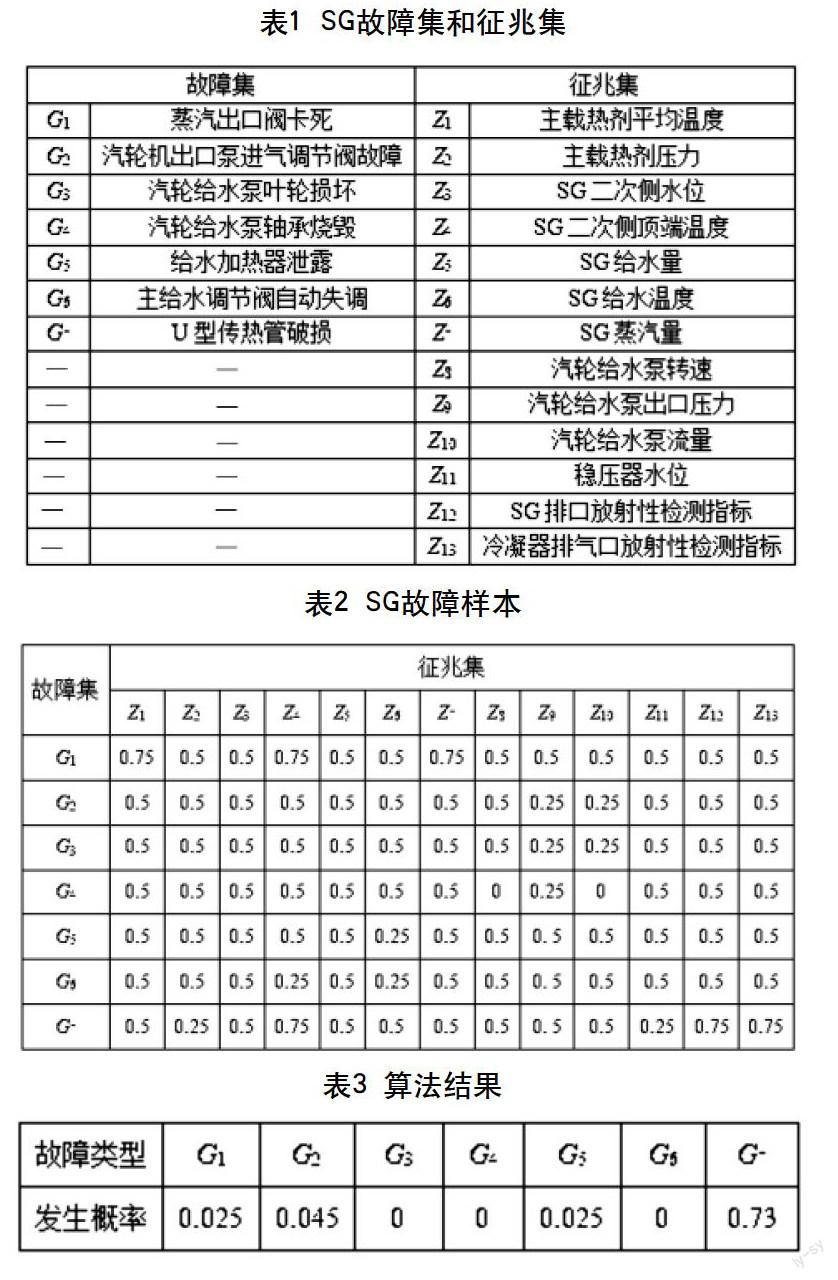
为了对上述模型进行验证，表1给出了故障集和征兆集，表2给出了区分征兆代表的参数在蒸汽发生器（SG）故障时所处的状态。其中，1.0为上限关机值，0.75为上限报警值，0.5为正常运行值，0.25表示下限报警值，0.0表示下限关机值。

当SG出现征兆群0.5，0.25，0.29，0.75，0.5，0.5，0.5，0.5，0.5，0.5，0.25，0.75，0.75时，利用2.2節所述故障诊断方法对SG进行故障诊断，其结果如图3所示。从图3可以看出，方法在第6次迭代后达到稳定，并且刚开始迭代时进化速度较快，并且在一定程度上也解决了局部最优问题。结果表明，该方法具有较好的收敛性，同时能够寻求到合适的全局最优。

将上述过程单独执行100次，其结果如表3所示。根据表3，可以得出结论：SG出现的故障为G7（U型传热管破损），该结论与文献[9，10]一致。对表3进行数据处理，得到该方法的平均查准率为88.5%，远大于文献[10]。

4 结语

采用概率因果模型，可以将诊断问题进行转化，而该转化过程需要利用形式化描述。如果求解概率因果模型时进行穷举，则很可能会引起组合爆炸，因此可以利用IWO算法来解决，进而实现核动力系统典型故障的诊断。实验结果也说明，将IWO方法嵌入概率因果模型进行故障诊断能够取得较好的效果。因此，上述方法可以在核动力系统故障诊断中得到有效应用，且具有较高的准确率和鲁棒性。

参考文献

[1] 付明玉，边信黔，史觊，等.船用核动力装置专家系统技术研究[J].核科学与工程，2002，22（3）：220-228.

[2] 陈志辉，夏虹，刘邈.核电系统故障诊断专家系统研究[J].核动力工程，2005，26（5）：523-527.

[3] 周刚，杨立.核电厂智能诊断方法研究的进展[J].原子能科学技术，2008，42（Suppl）：92-99.

[4] 张文星，纪有奎.专家系统原理与设计[M].武汉：武汉测绘科技大学出版社，1989.

[5] Peng Y，et al.A Probabilistic Causal Model for Diagnostic Problem Solving-part I：Integrating Symbolic Causal Inference with Numeric Probabilistic Inference[J].IEEE Trans.SMC，1987，17（3）：146-162.

[6] Peng Y.A Probabilistic Causal Model for Diagnostic Problem Solving-partⅡ：Integrating Symbolic Causal Inference with Numeric Probabilistic Inference[J].IEEE Trans.SMC，1987，17（3）：395-406.

[7] Rosenblatt F.The Percetion：A Probabilistic Model for Information Storage and Organization in the Brain[J].Cornell Aeronautical Laboratory，Psychological Review，1958（65）：386-408.

[8] Mehrabian A R，Lucas C. A Novel Numerical Optimization Algorithm Inspired from Weed Colonization[J].Ecological Informatics，2006，1（3）：355-366.

[9] 任鑫，孔衍，周碧松，等.改進遗传算法在船用和动力装置概率因果故障诊断中的应用[J].中国舰船研究，2013，1（8）：107-111.

[10] 孔衍，任鑫，王川，等.基于改进遗传算法的核动力装置故障诊断研究[J].原子能科学技术，2012，46（11）：1357-1361.