扩展二型模糊系统在飞机故障检测中的应用

孙曦浩

摘 要：随着二型模糊逻辑系统的蓬勃发展，在各个领域有着广泛的应用。该文在扩展二型模糊集合的基础上，提出了扩展二型模糊系统，并给出相应的设计算法。考虑到扩展隶属函数取值范围的增加，可将系统残差输出划分为正常、异常和故障三个状态。新增加的异常状态可以得到更为清晰的诊断结果，能有效的避免误诊和漏诊。针对非线性飞机模型，仿真结果表明了该方法的有效性。

关键词：二型模糊集合 故障诊断 扩展二型模糊系统

中图分类号：TP273 文献标识码：A 文章编号：1674-098X（2015）09（b）-0093-03

Application of expanded type-2 fuzzy system in aircraft fault detection

Sun Xihao

（Wuxi Lake Tai College， Wuxi Jiangsu， 214000， China）

Abstract：With the vigorous development of the type-2 fuzzy logic system，numerous applications are used in various fields. In this paper，we proposed expanded type-2 fuzzy system based on expanded type-2 fuzzy set.Moreover，corresponding design algorithm is given.As we added negative values to the membership function，the residual error outputs could be clearly divided into three statuses：normal，abnormal，fault.The increase of new state could present more clear results，which effectively avoid misdiagnosis and missed diagnosis.The simulation of aircraft indicates efficiency of method.

Key Words：Type-2 fuzzy sets；Fault diagnosis；Expanded type-2 fuzzy system

故障诊断是自动控制中热点研究方向[1]，它是系统有效性和可靠性的先决条件。一型模糊逻辑系统已成功应用于容错控制与故障诊断[2-4]，而其主要方法是利用模糊集合来表示残差或观察器，通过残差自适应方法[5]、滑模观察器[6]、模糊分类器[7]等解决故障诊断问题。但目前的模糊故障诊断方法，只考虑根据故障征兆来肯定故障的程度，而沒有考虑故障征兆从而否定故障。另外，在描述故障特征时，由于含有大量的不确定性和采用语言变量的描述困难，使得隶属函数的设计也存在一定困难。二型模糊系统的提出有效地解决了隶属函数的设计难度，而且能够描述更高层次的不确定性[8]。近年来，越来越多的学者投身于二型模糊系统的研究，并将其应用于通信、金融、控制及医疗等各个领域[9-12]。该文根据扩展二型模糊逻辑系统，增加扩展隶属函数取值范围，将系统残差的输出清晰的划分为三个状态：正常、异常和故障。新增加的状态，能够有效的避免误诊和漏诊。针对某非线性飞机模型的仿真结果表明了其有效性。

1 扩展二型模糊系统

扩展二型模糊系统，是在二型模糊系统的基础上，将二型模糊系统中前件和后件的二型模糊集合，用扩展的二型模糊集合替换，而相应的运算方法不变，不同的是二型模糊集合的隶属函数是区间上的常规隶属函数，而扩展的二型模糊集合的隶属函数是区间上的扩展的一型隶属函数[13]。

考虑p个输入和一个输出的扩展二模糊系统，使用单点模糊化，重心去模糊的降型方法[13-14]和If-Then规则的如下形式：

：if is and is and … and is then is

则：

（1）

其中：和分别是扩展的二模糊集合；表示第条规则后件模糊集合的重心；。是区间的扩展隶属函数。

由于该系统是在常规模糊系统中，将控制规则的前件和后件取为扩展的二型模糊集合，隶属函数采用区间型。

在利用常规的隶属函数进行故障诊断时，诊断的结果只有两个：正常和故障两状态，另外，由于故障特征的提取存在许多不确定性，利用扩展的二型模糊集合进行诊断时，诊断结果是具有三个状态：正常、异常和故障。可以有效的避免误诊或漏诊。

将扩展的二型模糊集合引入故障诊断系统，建立基于扩展二型模糊系统的故障诊断系统。

假设diag，是执行器故障矩阵，并且满足；则

（1）时，表示系统正常的程度为（正常）；

（2）时，表示系统不正常（异常）；

（3）时，表示系统故障的程度为（故障）。

其中，。

为了应用上的方便，将模糊规则中的前件和后件中的扩展的二型隶属函数设置为中的一型区间函数，此时（1）式简化为：

（2）

权重：

（3）

其中，均属于区间。，假设此处的隶属函数均为区间数，实际计算中每次只需两个集合。

扩展的二模糊系统的设计方法是在二模糊系统的设计步骤上，用扩展的二型模糊集合代替二型模糊集合，模糊系统的设计算法相应修改如下[15]：

令，，

（），按照都取右端点的方法，即令：，不失一般性，假设排序如下：；

令對（，），用（3）式计算：

；

求使；

令和，用（3）式计算；

判断：若成立，则停止，否则到（f）。

令，go to （b）。

2 仿真实例

该文所采用的数据来源于某非线性飞机模型的输出数据。设定飞机飞行高度为5000m，飞行马赫数为0.6，设置采样时间为0.012 s。采集如下数据源：正常状态数据，右副翼卡死在-20°、-8°、-16°、…、-4°、、、、、、…、16°、18°、20°数据，右副翼损伤10%、15%、20%、…、90%、95%、100%的数据，右平尾卡死在、-10°的数据，右平尾损伤20%、50%、100%的数据，方向舵损伤100%的数据，总共6种状态数据，共945组采样数据。每组采样数据有攻角（Alpha）、侧滑角（Beta）、滚转角速度（Wx）、俯仰角速度（Wz）、偏航角速度（Wy）、偏航角（Psi）、俯仰角（Theta）和滚转角（Gamma）共8个变量。

设某型歼击机结构故障诊断技术指标如下。

（1）故障诊断灵敏度。损伤：≥20%；卡死：≥1度。

（2）故障诊断精度。（范围精度）

右副翼卡死：～±20°≥90%

右副翼损伤：20%～100%≥90%

右平尾卡死：和-10°≥90%

右平尾损伤：20%、50%和100%≥90%

方向舵损伤：100%≥90%

对某歼击机构造如下的决策表，

其中表示不同歼击机结构故障状态；，其中表示条件属性，分别定义为攻角（Alpha）、侧滑角（Beta）、滚转角速度（Wx）、俯仰角速度（Wz）、偏航角速度（Wy）、偏航角（Psi）、俯仰角（Theta）和滚转角（Gamma）；表示决策属性，分别定义为无故障、右副翼卡死、右副翼损伤、右平尾卡死、右平尾损伤和方向舵损伤。

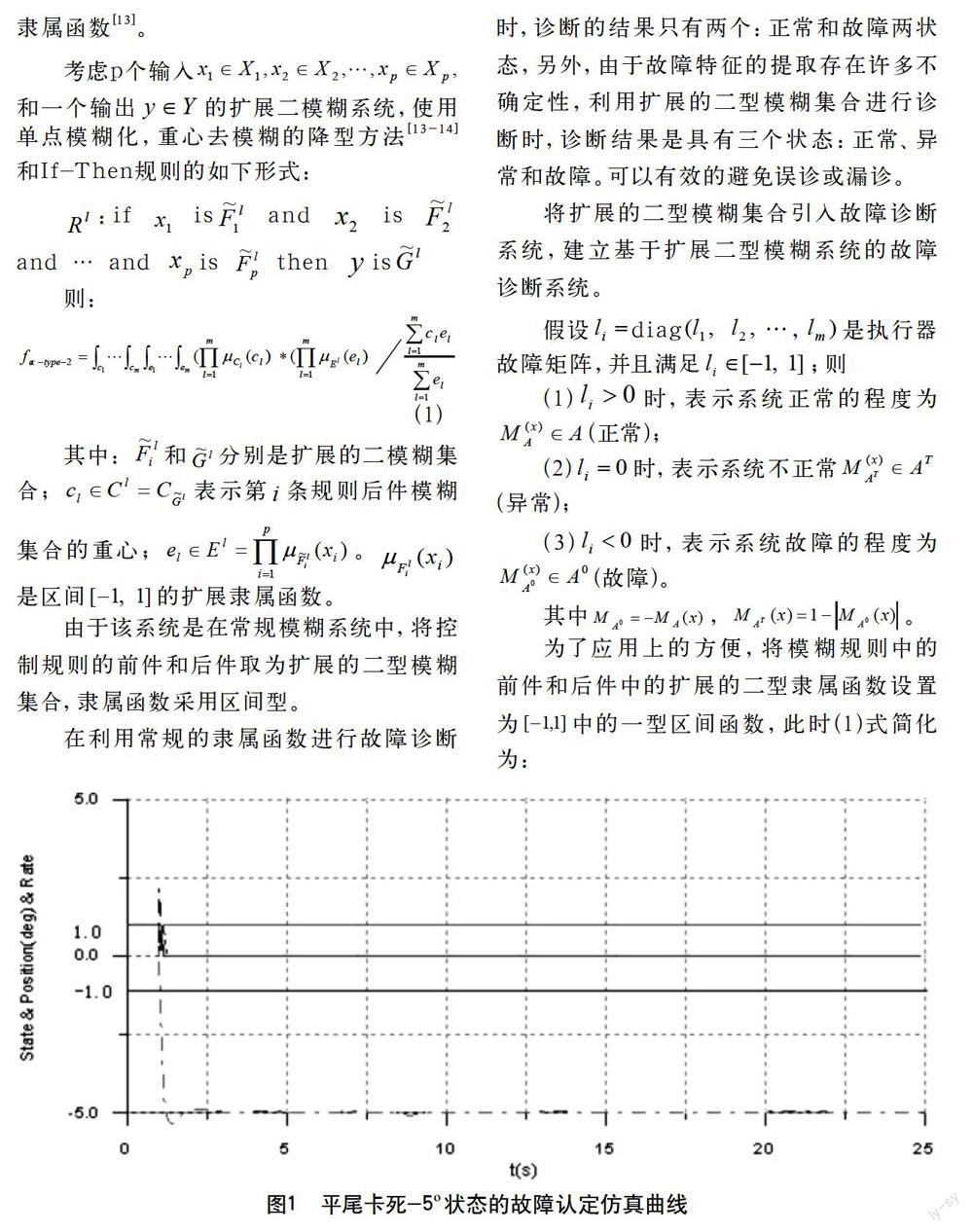
2.1 右单平尾卡死-5?故障认定仿真

1.0为正常飞行状态标志位，-1.0为故障状态标志位。最初，可以观测到正常飞行状态标志位为1，其余标志位均为0，表明飞机处于正常飞行状态。经过一个瞬时振荡，正常飞行状态标志位为0，右平尾升降舵卡死故障状态标志位为-1，其余标志位均为0，表明飞机右平尾升降舵出现卡死故障。同时显示出右平尾升降舵卡死位置在-4.47?至-5.38?之间，仿真时段内平均值为-4.99。

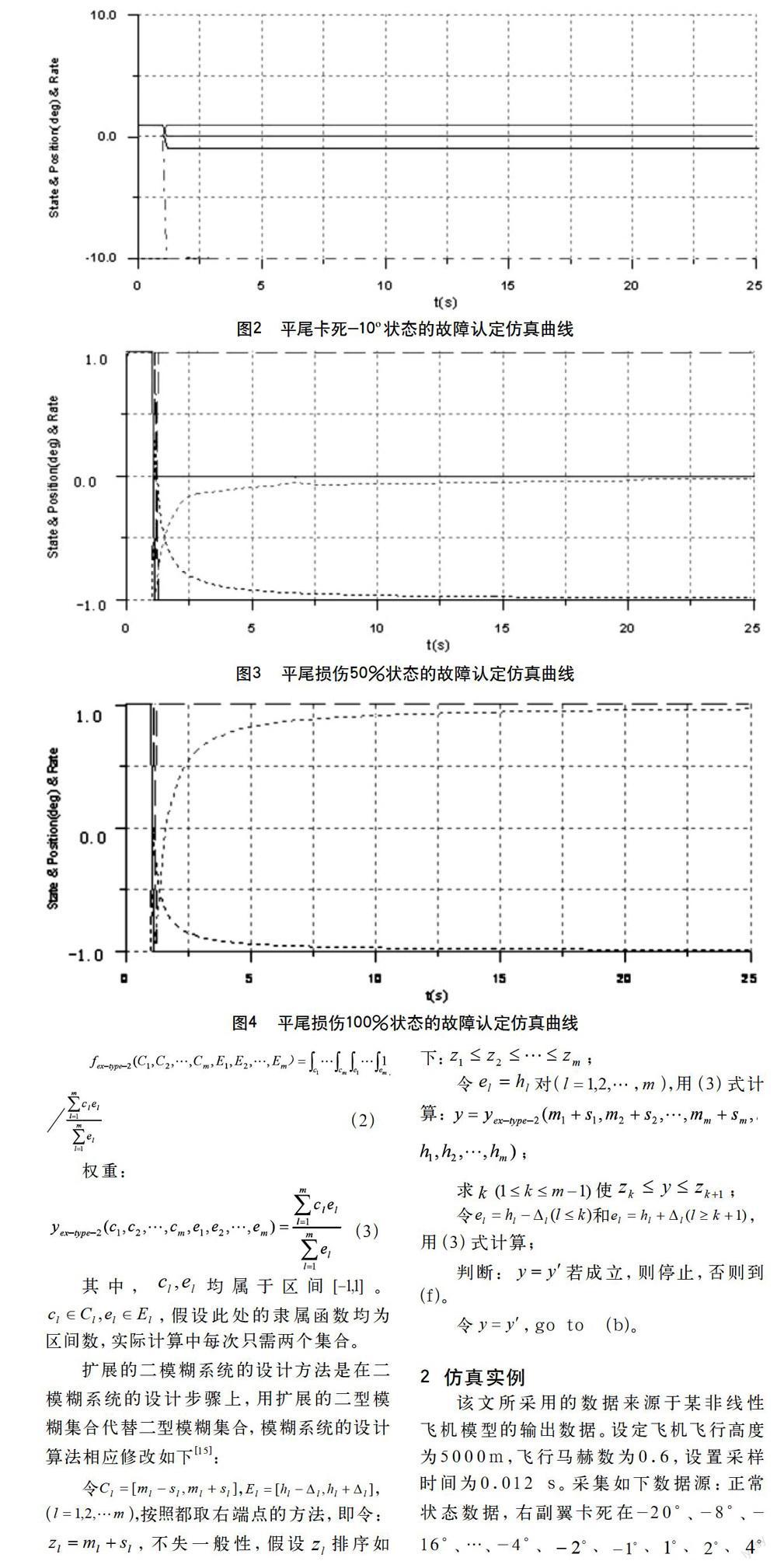
2.2右单平尾卡死-10?故障认定仿真

初始，可飞机处于正常飞行状态。经过一个瞬时振荡，正常飞行状态标志位为0，右平尾升降舵卡死故障状态标志位为-1，其余标志位均为0，表明飞机右平尾升降舵出现卡死故障。同时显示出右平尾升降舵卡死位置在-9.71?至-10.00?之间，仿真时段内平均值为-9.99?。

2.3 右单平尾折断50%故障认定仿真

初始，可以观测到正常飞行状态标志位为1，其余标志位均为0，表明飞机处于正常飞行状态。经过一个瞬时振荡，正常飞行状态标志位为0，右平尾升降舵损伤故障状态标志位为-1，其余标志位均为0，表明飞机右平尾升降舵出现损伤故障。同时显示出右平尾升降舵损伤比例在17.67%至49.08%之间，仿真时段内平均值为49.03%。

2.4 右单平尾折断100%故障认定仿真

初始，飞机处于正常飞行状态。经过一个瞬时振荡，正常飞行状态标志位为0，右平尾升降舵损伤故障状态标志位为-1，其余标志位均为0，表明飞机右平尾升降舵出现损伤故障。同时显示出右平尾升降舵损伤比例在17.42%至98.76%之间，仿真时段内平均值为98.76%。

3 结语

该文在二型模糊系统的基础上，结合扩展二型模糊集合，提出了扩展二型模糊系统，并用于非线性飞机模型的故障诊断。扩展隶属函数增加了负值，相比于传统模糊系统的结果，提供了更多的输出信息，有效的避免了误诊和漏诊。

参考文献

[1] 周东华，王庆林.基于模型的控制系统故障诊断技术和最新进展[J].自动化学报，1995，21（2）：224-247.

[2] Bennett S M，Patton R J，Daley S.Sensor fault-tolerant control of a rail traction drive[J].Control Engineering Practice，1999（7）：217-225.

[3] Shields D N.Observer design and detection for nonlinear descriptor systems[J].International Journal of Control，1997，67（2）：153-168.

[4] Lopez C J， Patton R J，Daley S.Takagi-Sugeno Fuzzy Fault-Tolerant Control of an Induction Motor[J].NeuraComputing&Applictions，2000（9）：19-28.

[5] Schneider H，Frank P M.Fuzzy logic based threshold adaption for fault detection in robots[C]//Proc 3rd IEEE Conf Control Applications，1994：1127-1132.

[6] Edwards C，Spurgeon S K，Patton R J，et al.Sliding mode observers for fault detection[C]//Proc IFAC SAFEPROCESS97，1997：522-527.

[7] Andre L，Walmir C，Fernando G. Adaptive fault detection and diagnosis using an evolving fuzzy classifier[J].Information Sciences，2013（220）：64-85.

[8] Mendel J M，John R I.Type-2 fuzzy sets made simple [J].IEEE Transactions on Fuzzy Systems，2002，10（2）：117-127.

[9] Liang Q，Mendel J M.MPEG VBR video traffic modeling and classification using fuzzy techniques[J].IEEE Transactions on Fuzzy Systems，2001，9（8）：183-193.

[10] Hernandez M，Mendez G M. Modelling and prediction of the MXNUSD exchange rate using interval singleton type-2 fuzzy logic systems [J].IEEE Computational Intelligence Magazine，2007，2（1）：5-8.

[11] John R I，Innocent P R，Barnes M R.Type-2 fuzzy sets and neuro-fuzzy clustering of radiographic Tibia Images[C]//IEEE International Conference on FuzzySystems，Anchorage，AK，1998：1373-1376.

[12] Hani A，Hagras A.Hierarchical type-2 fuzzy logic control architecture for autonomous mobile robots [J].IEEE Transactions on Fuzzy Systems，2004，12（4）：524-539.

[13] Karnik N K，Mendel J M， Liang Q.Type-2 fuzzy logic systems [J].IEEE Transactions on Fuzzy Systems，1999，7（6）：643-658.

[14] Liang Q，Mendel J M.nterval type-2 fuzzy logic systems [C]//IEEE International Conference on Fuzzy Systems，1999：643-658.

[15] 李莉，李醫民，孙玉坤.基于扩展Type-2模糊集的故障诊断方法[J].系统工程与电子技术，2008（30）：2280-2283.