基于智能计算的非线性系统辨识算法研究及其应用

庄丽艳

摘 要：在智能计算中，非线性系统是智能计算生产系统中重要的组成部分。随着生产水平以及规模的不断提升，其生产系统结构的复杂性也逐渐提升。同时非线性的特性也越来越多样化，非线性系统越来越受到人们的关注与青睐，但从目前的使用情况来看，简单的非线性已无法满足当下智能计算的生产需求，因此，对智能计算的非线性系统识别算法进行进一步研究十分重要。该文主要对智能计算的非线性系统辨识算法研究及其应用进行详细阐述，以便对智能计算的非线性系统辨识带来一定的启发。

关键词：智能计算 非线性系统 辨识算法 研究应用

中图分类号：TP13 文献标识码：A 文章编号：1672-3791（2015）09（b）-0060-02

在智能计算的非线性系统辨识算法中，主要采用模块化非线性模型，因为其不仅内部连接方便，而且結构简单，是使用最多且最普遍的一种模型。其所包括的模型类型有四种，即W-H模型、H-W模型、W模型和H模型。由于热工系统具有结构复杂性以及规模巨大性，其生产过程中需采用多样化的非线性系统。因此在热工系统中，一定要对检测以及执行变送器进行充分研究，确保其非线性特性与热工系统的生产需求相符合。

1 非线性系统中执行器的基本概况

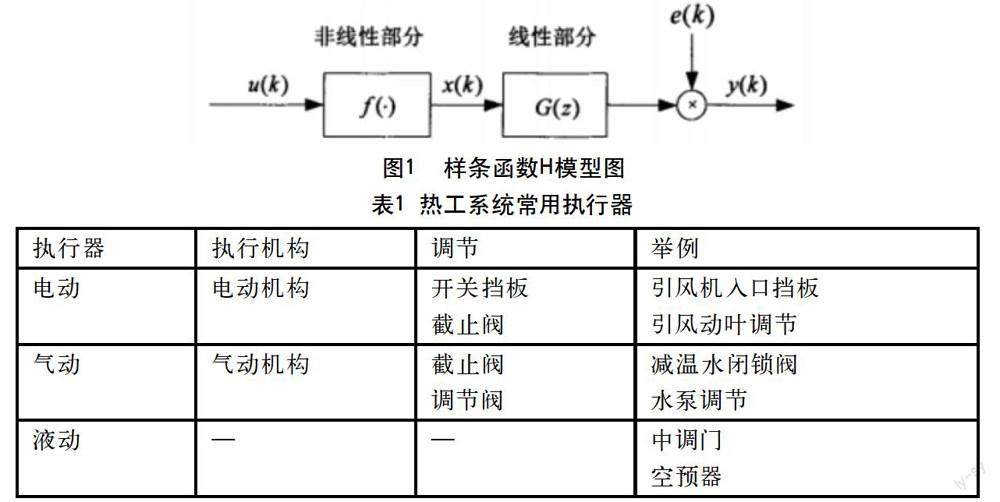
在非线性系统中，执行器主要包括两种，一种是控制机构，另一种是执行机构。在执行器中，控制机构一般包括调节阀、截止阀等，执行机构主要包括气动、液动、电动，热工系统的执行器主要使用方法如表1所示。

2 非线性系统辨识概述

2.1 非线性系统辨识的必要性

工业企业是推动社会经济发展的核心力量，也是推动我国经济发展的重要组成部分，工业企业想要发展，其生产系统必须满足经济性与安全性要求。但是由于工业企业生产系统的结构比较复杂，想要提升工业企业生产系统控制的有效性，最主要的方法就是充分研究非线性系统的辨识性。辨识技术可帮助人们在表述被研究对象时，尽可能准确定位其之间的定量关系，只有企业的生产系统与智能计算的辨识系统需求相符合，才能实现企业生产系统的经济性与安全性。

2.2 非线性系统辨识的定义

系统辨识又称为系统同定和系统识别，《中国大百科全书》对系统辨识的解释为根据系统输入或输出时间函数，确定系统行为的数学模型，是现代控制理论的一个分支。辨识是一种实验统计的建模方法，即系统辨识主要研究怎样利用对位置系统的实验数据或在线运行数据建立系统的数学模型，同时也是在输入或输出数据中提取被研究对象数学模型的一种统计方法。

2.3 非线性系统辨识的应用

非线性系统辨识的应用主要表现在以下几方面。（1）进行预报。准确的预报对企业发展具有非常重要的意义，其有利于企业制定科学、合理的决策方案；（2）进行规划。正确的模型可为正确的规划提供最优规划方案，继而促进工业企业的经济发展；（3）进行仿真研究；有了模型，可对系统进行仿真研究，从而制定可行策略；（4）进行生产过程的故障诊断。若模型参数发生变化，则表明生产过程出现故障或变化；（5）进行控制。有了数学模型，可对生产系统进行最优控制。

此外系统辨识的三要素主要包括：数据、模型、准则。其中数据主要是指数据的输入和输出，同时其也是辨识的基础；模型有静态模型、动态模型、线性模型以及非线性模型之分；准则主要包括等价准则、输出误差准则、输入误差准则、广义误差准则四种[1]。

3 样条函数H模型辨识算法的研究与应用

在工业企业生产系统中，其智能计算系统具有一定的非线特性，随着企业生产系统规模的不断扩大，智能计算的复杂性也逐渐增加。因此对其辨识算法进行优化成为了促进企业经济发展的首要条件与必要前提。在智能计算的非线性系统辨识算法中，样条函数H模型辨识算法最为常用。样条函数H模型辨识算法模型图如图1所示。

样条函数模型差分方程为：

在此公式中，线性部分为

从目前工业企业智能计算的情况来看，H模型在企业生产系统中的运用越来越多，且具有较强的使用性。样条函数H模型不仅可提升非线性系统辨识效率，而且计算机对其比较容易识别[2]。由于样条函数其本身就是分段函数，因此，用其进行建模，与企业实际生产系统的需求更加接近。此外，在数据比较多时，可采用K均值算法，这样不仅可减少辨识参数，还可大幅度提升辨识效率。

4 量子粒子群H模型辨识算法的研究与应用

量子粒子群H模型，辨识算法是系统辨识研究中重要的组成部分，同时也是最常用的优化工具。但从以往非线性辨识系统的使用情况来看，其仍然存在较多的不足与缺陷，如收敛慢等。为解决此问题，行业内专家对其进行了全面改进，如后来的自适应变异法、杂交PSO算法等，对其收敛慢具有一定的改进作用。PSO算法是一种比较常用的方法，其主要采用粒子位置，扩展算法实现粒子移动，然后根据粒子的移动情况搜索最佳位置的粒子，对粒子位置进行变异操作，实现算法的收敛速度[3]。

粒子状态更新规则如下所示：

其中

在POS算法中，增加种群的多样性，可避免收敛早熟，由量子非门实现的变异操作过程为：

其中变异概率是pm，粒子随机数为rnd，如果pm>rndi，随机选择[D/2]量子位，对概率富进行对换，粒子自身角度和位置不变[4-5]。其辨识算法的步骤为（1）根据POS算法循环，进行群体初始值设定；（2）计算EA值，执行解空变换，求出循环最优值；（3）采用旋转门，进行量子更新；（4）计算粒子异变概率；（5）对量子群法进行判断，若满足则算法结束，否则对2、4步进行重复，直到满足[6-7]。

5 网络化W模型辨识算法的研究与应用

网络化W模型，是一种典型的非线性模型，同时也是辨识系统运用最多的模型，本文主要采用两种网络模型，表述W模型的非线性，即RBF、BP[8-9]。网络化W模型差分方程表示为：

其中n和m分別为此公式A（q-1）和B（q-1）多项式。BP网络模型具有较强的映射功能，其主要运用动量项，来提升模型的速度，此外为了进一步确保模型的稳定性与速度，BP算法在进行模型训练时应遵守以下公式，

其中y（k）、yr（k）表示网络W模型的输出值和第k个样本的真值。为加强PB算法的速度，在修正权值时引入动量项算法为：

其中k时刻的负梯度为D（k），动量系数为：

RBF网络W模型其 静态RBF系统的输入是动态系统的输出，网络W模型的输出是RBF系统输出。

RBF线性动态系统输入公式为：

RBF线性动态系统输出公式为：

通过采用RBF和PB对网络W模型进行优化，其对生产系统具有良好的辨识度和泛化能力，特别是使用于企业生产系统中数据的辨识。辨识就是在输入和输出数据的基础上，确定所测系统的模型[10-11]。

6 量子粒子群H-W模型辨识算法的研究于应用

在非线性模型中，量子粒子群H-W模型，量子粒子群模型主要有两种形式，即多项式H-W、神经网络H-W。该文主要对网络化H-W进行充分研究。网络化H-W差分方程为：

线性部分：

其中m和n的多项式为B（Z-1）和A（Z-1），系统延时表示为d。在进行量子粒子群H-W模型辨识中。量子粒子群H-W模型辨识算法应用，可根据生产系统的输出和输入变化进行预算，此外还可通过最小均方误差，对量子粒子群H-W模型的系数进行纠正，然后根据算法求出该模型的最优参数，模型的结构要合理，输入信号必须是持续激励的，同时数据还要充足，辨识模型参数的个数应尽可能少，以最简单的模型表述所描述的对象特征。量子粒子群H-W模型其不仅应用广泛，且适用性比较强，可大幅度满足生产系统的需求[12]。

7 结语

综上所述，在实际生产中，采用智能计算的非线性系统识别算法，可大幅度提升生产力。本文主要以生产系统的构成为主要出发点，对智能计算的非线性系统辨识算法进行充分研究，采用的研究方法是非线性模块化模型。通过对系统中传感器以及执行器的研究，得出在智能计算的非线性系统辨识算法中采用模块化模型的重要性，其可有效满足非线性系统的辨识算法。在以后智能计算的非线性系统辨识算法的研究中，应对模块建模以及群体智能算法进行充分研究，以便对控制系统进一步优化。

参考文献

[1] 刘朝华，李小华，周少武，等.面向永磁同步电机参数辨识的免疫完全学习型粒子群算法[J].电工技术学报，2014，5（12）：22-25.

[2] 刘辉煌，莫宪，饶彬.基于Lotka-Volterra模型的中国股票市场非线性特征--一个生态学的视角[J].财经理论与实践，2014，4（23）：12-16.

[3] 邓泽林，谭冠政，何锫.非线性神经元电活动的数学模型及其分析方法与计算机仿真研究[J].计算机研究与发展，2013，8（23）：17-20.

[4] 徐岩，王波，李鹏.基于检测系统非线性相关性的相空间重构时间延迟估计震[J].动与冲击，2014，8（13）：25-27.

[5] Wang Dongfeng，Zhang Jinying，Yuan Shitong，Ren Yanyan. Robust synchronization of fractional-order PMSM chaotic system[J].Journal of Modern Mathematics Frontier，2013，2（4）：120-124.

[6] 孟丽，韩璞，任燕燕.基于多目标粒子群算法的PID控制器设计[J].计算机仿真，2013，30（7）： 388-391.

[7] Ren Yanyan，Wang Dongfeng，Liu Changliang，Han Pu.PSO and spline function-based hammerstein model and its application to system identification[J].Intelligent Information Management Systems and Technologies，2012，8（4）：421-428.

[8] Ren Yanyan，Wang Dongfeng，Liu Changliang，Han Pu. Identification of thermal process using wiener model based on PSO and DNN[J].Intelligent Information Management Systems and Technologies，2012，8（1）：11-20.

[9] Srinivasan A.，Lakshmi P. Identification and control of Wiener type process applied to real-time heat exchanger[J]. Asia-Pacific Journal of Chemical Engineering，2008，3（6）：622-629.

[10] Nafar M Gharehpetian G B Niknam T.Using Modified Fuzzy Particle Swarm Optimization Algorithm for Parameter Estimation of Surge Arresters Models[J].International Journal of Innovative Computing Information and Control， 2012，8（1B）： 567-581.

[11] Zahara Er.，Hu C.H.Solving constrained optimization problems with hybrid particle swarm optimization[J]. Engineering Optimization， 2008，40（11）：1031-1049.

[12] Deng W.，Chen R.，Gao J.et ah A novel parallel hybrid intelligence optimization algorithm for a fimction approximation problem [J].Compuers & Mathematics with Applications 2012，63（1）： 325-336.