模块化机械臂轨迹规划算法仿真研究*

□ 嵇建成 □ 郭 帅 □ 薛 卉 □ 王志勇

1.上海大学 上海市智能制造及机器人重点实验室 上海 200072

2.上海电气集团股份有限公司 中央研究院 上海 200070

模块化机械臂轨迹规划算法仿真研究*

□ 嵇建成1□ 郭 帅1□ 薛 卉2□ 王志勇1

1.上海大学 上海市智能制造及机器人重点实验室 上海 200072

2.上海电气集团股份有限公司 中央研究院 上海 200070

基于OpenGL模块化机械臂三维仿真模型，阐述了竖直六自由度、悬挂六自由度以及竖直七自由度等多种模块化机械臂的运动学求解，实现了三次多项式、五次多项式、BDJP等多种插补算法，完成了在笛卡尔空间层中以直角坐标路径控制和以BDJP法实现圆弧轨迹插值控制。另外，在模块化机械臂实验平台上，针对各种运动学求解算法编写了验算程序，完成了竖直六自由度同步在线控制、悬挂六自由度指令控制走“中”字和圆等实验，证明了算法的正确性和精确性。

轨迹规划 OpenGL 模块化机械臂

服务机械臂不仅在空间探测、军事战场、家庭服务领域有着重要的应用价值和广阔的发展前景，而且在工业生产、医疗保健领域也存在很大的市场潜力［1］。许多科研机构竞相开展了对服务机械臂的研究，但由于服务机械臂涉及轨迹规划、遥控操作等复杂技术，使服务机械臂的仿真控制技术发展缓慢。

笔者以德国Schunk模块化服务机械臂为研究对象，基于OpenGL完成了服务机械臂仿真控制平台的研发，实现了三维仿真模型和实物模型的轨迹规划和同步动作，为进一步实现无线遥控操作技术打好基础。

1 简介

平台的硬件部分是根据德国Schunk模块化服务机械臂电气和硬件要求完成服务机械臂组装，通过CAN总线和模块API函数，实现硬件软件控制［2～4］。软件层面，上位计算机根据仿真模型和硬件模型结构，完成运动学求解，如图1所示。

轨迹规划是实现PTP运动、过路径点运动、直线运动、圆弧运动以及解析平台指令的基础，决定着服务机械臂运动的精度［5～7］。模块化机械臂仿真软件的轨迹规划器主要在关节层采用抛物线过渡、三次多项式、过路径点三次多项式、过路径点五次多项式等插

值算法，实现关节运动轨迹规划；在笛卡尔空间层采用直角坐标路径控制法、BDJP法等插补算法，实现走直线、圆弧等轨迹运动［8～12］；其它两层实现硬件模型和仿真模型的运动控制功能。指令系统负责服务机械臂指令文件的编译、调试及执行，软件交互界面负责显示三维仿真模型的运动过程及用户交互。通过模块的光电编码器采集模块的位置和速度，驱动仿真模型动作，监视模型末端位置情况［13～16］。本文重点阐述基于BDJP插值算法的轨迹规划工作。

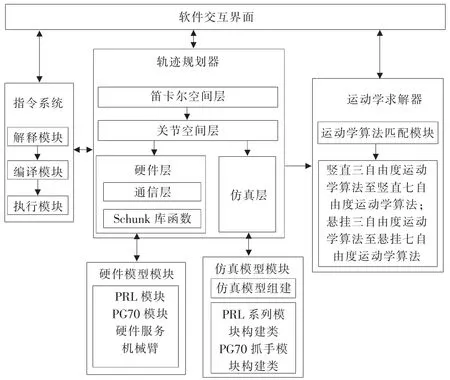
▲图1 模块化机械臂仿真平台软件结构

2 基于多项式轨迹规划算法

笔者设计的轨迹规划器根据用户指令，采用抛物线过渡、三次多项式、五次多项式、过路径点三次多项式、过路径点五次多项式插值算法，在关节空间实现了服务机械臂的PTP和过路径点运动；采用直角坐标路径法和BDJP插值法，在笛卡尔空间实现服务机械臂的直线和圆弧功能。

2.1 抛物线过渡插值算法

Schunk运动模块接口函数提供了一种梯形运动方式，其速度曲线如图2所示。该接口函数能实现带抛物线过渡域的线性轨迹（LSPB），即抛物线过渡插值算法，手臂运行可分为3个过程：加速、匀速和减速，假设初始位置为θi，初始加速度为，手臂最大速度为，终止时加速度为，终止位置为θf。在［0，ta］时间段手臂处于加速过程，加速度为，加速时间为ta；在［ta，tf-td］时间段手臂各关节处于匀速过程，速度为，匀速运行时间为tu；在［tf-td，tf］时间段内手臂各关节减速运行直至停止，减速时间为td。

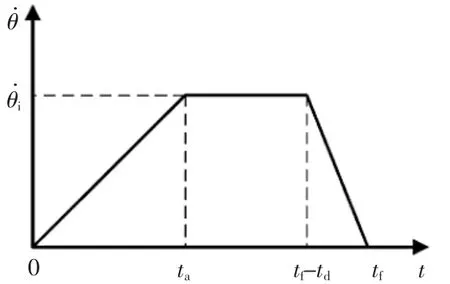
▲图2 梯形插值V-T图

根据抛物线过渡运行特点可得：

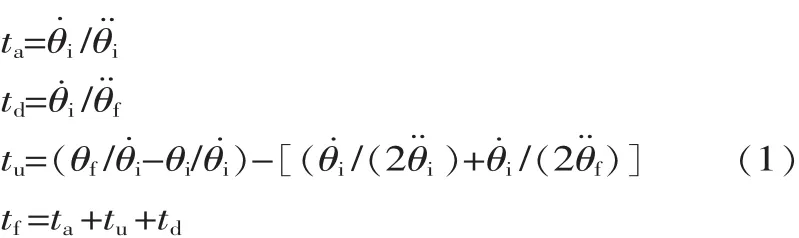
由式（1）得手臂插值函数为：

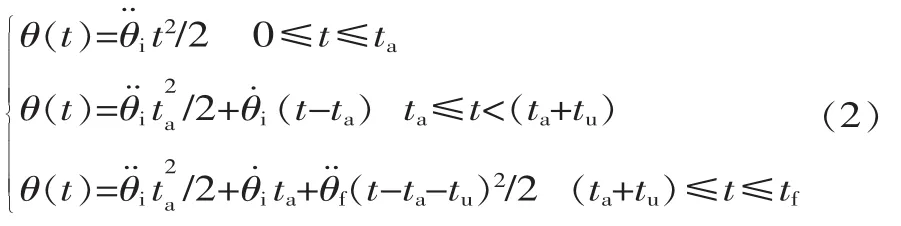
为保证各关节同时启停，对各关节的运行基于V-T图进行时间归一化处理，其处理过程如图3所示。

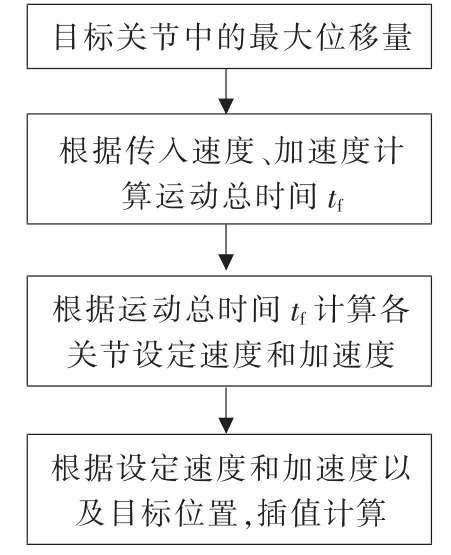
▲图3 时间归一化处理

以悬挂六自由度服务机械臂为例，设：初始位置各关节为0°，目标位置关节角度为 （20，30，40，-26，-15，-23），速度为10°/s，加速度为20°/s2，进行实验。用该算法插值时，服务机械臂各关节速度时间曲线如图4所示。

由图4可知，采用该算法能实现PTP运动，但在关节速度为零或加速度发生突变时，电机的速度时间曲线有一定幅度的振荡，振荡主要由加速度突变引起。

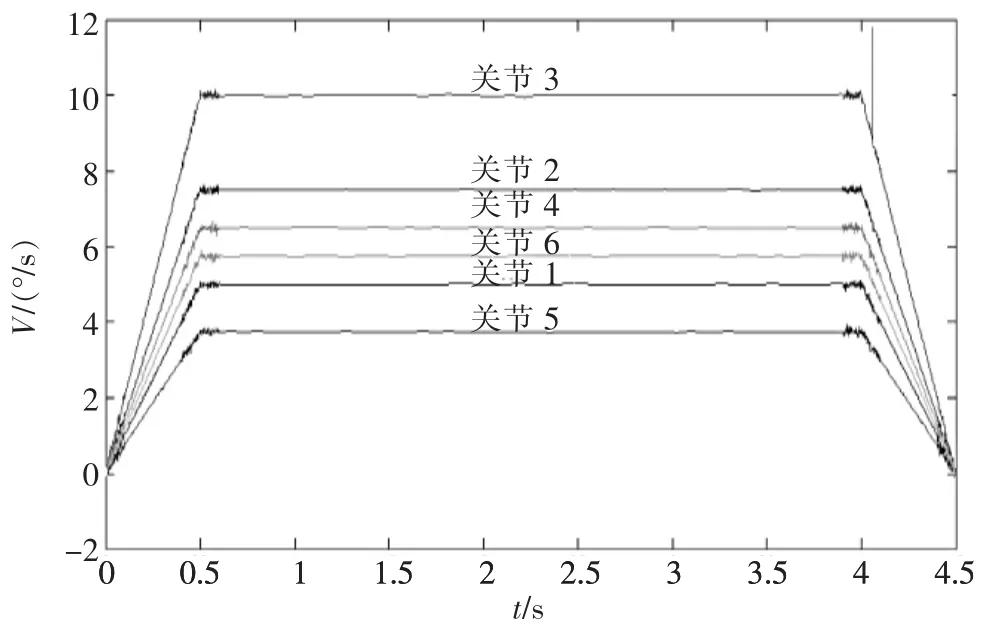
▲图4 抛物线插值V-T图

2.2 三次多项式插值算法

为克服加速度突变导致的电机运动振荡，采用了三次多项式插值算法来实现关节空间的轨迹规划。设

关节空间运动的三次多项式为：

由于关节运动的目标位置和运动时间tf由指令系统指定，并且起始点和终止点速度为零，因此可得4个约束方程。设起始点位置为θ0、终止点位置为θf，则约束方程组为：

求解上述线性方程组可得：

各组关节根据式（5）求出三次多项式因子，然后按照式（3）进行关节插值运动。需要注意的是在完成插值运动后要用软件限幅滤波法滤波，以保证关节运动在允许的范围内。

以悬挂六自由度服务机械臂为例进行实验，让其从初始位置（0，0，0，0，0，0）运动到（30，25，60，42，-34，-28），运动时间为5 s。用该算法实验时，服务机械臂各关节速度时间曲线如图5所示。可见，在采用三次多项式插值算法的情况下，服务机械臂能实现PTP运动，而且运动更加平稳，振荡明显减弱。

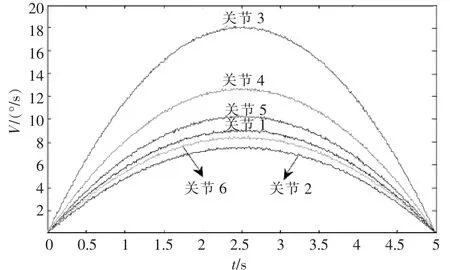
▲图5 三次多项式插值V-T图

2.3 过路径点连续三次多项式插值算法

为实现关节空间的过路径点连续运动，笔者设计了过路径点连续三次多项式插值算法。算法的思想是在多组关节目标位置和各目标位置运动之间的时间值由指令系统指定后，采用启发模式设定关节各路径点的速度，再按照三次多项式插值算法完成插值运算，最后采用限幅滤波法保证其在关节工作范围内。

采用启发模式设定路径点速度，如图6所示。图中，θ0为起始点，θD为终止点，θA、θB和θC为路径点。假设用直线段把这些路径点依次连接起来，如果相邻线段的斜率在路径点处改变符号，则把速度设定为零；如果相邻线段不改变符号，则选取路径点两侧线段斜率的平均值作为该点的速度。因此，根据指令，系统就能够按此规则自动生成相应的路径点速度。

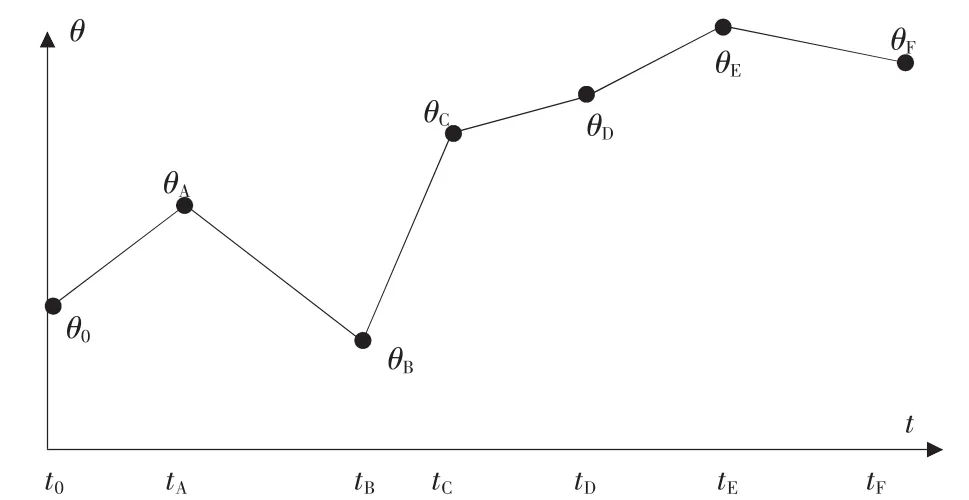
▲图6 路径点速度启发原理图

通过速度启发模式获得路径点的速度后，过路径点连续三次多项式插值问题转换为已知起始点位置和速度、终止点位置和速度、运动时间的三次多项式插值问题。设起点位置为θ0，起点速度为，终止点位置为θf，终止点速度为，起点运动到终点的运动时间为tf。

则根据约束条件可得：

解方程组（6）得：

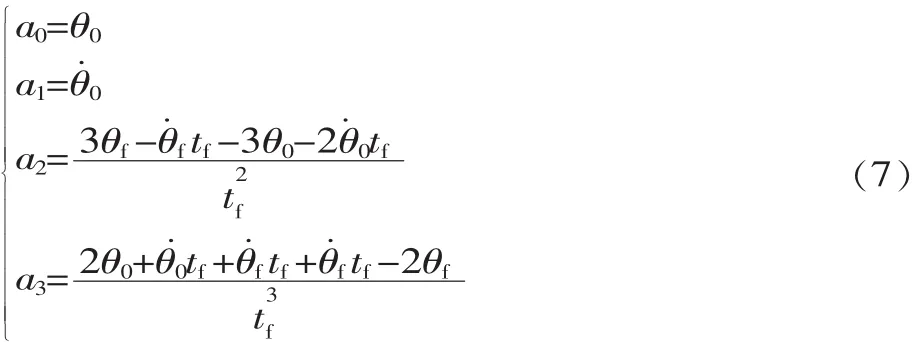
由式（7）求得三次插值多项式，并结合三次多项式式（6）循环完成过路径点的连续插值，最后利用限幅滤波法进行滤波。

以悬挂六自由度服务机械臂为例进行实验，初始位置为（0，0，0，0，0，0），第一个路径点为（20，30，40，23，-34，-28），时间是5 s，第二个路径点为（35，23，46，31，0，13），时间是5 s，第三个路径点为（41，21，52，20，15，26），时间是4s，终 止 点 为（60，31，62，31，36，30），时间是3 s。用该算法进行轨迹规划时，服务机械臂各关节速度时间曲线如图7所示。说明：由于模块返回速度信息不具有方向性，因此图7中部分关节速度曲线发生了翻折。

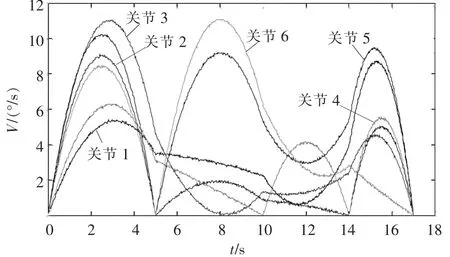
▲图7 过路径点三次多项式插值V-T图

由图7可知，过路径点三次多项式插值算法，能实现服务机械臂关节空间的过路径点连续轨迹运动，但由于路径点速度、加速度不连续，导致路径点连接处的振荡幅度偏大。

2.4 过路径点五次多项式实现过路径点连续运动

为克服路径点连接处振荡较大问题，采用过路径点五次多项式实现过路径点连续运动。算法采用速度和加速度启发模式，设定各个路径点关节的速度和加速度，启发规则与方式，如图6所示。完成速度和加速启发后，问题转化为：已知起始点和终止点的位置、速度、加速度及运动时间的三次多项式插值问题。设起始点位置为θ0，起始点速度为，起始点的加速度为，终止点位置θf，终止点速度为，终止点的加速度为，运动时间为tf。设关节五次插值多项式为：

根据式（10），求解出各路径点五次多项式参数进行插值，再利用限幅滤波法进行滤波。

以悬挂六自由度服务机械臂为例进行试验，初始位置为（0，0，0，0，0，0），第一个路径点为（20，30，40，23，-34，-28）、时间是5 s，第二个路径点为（35，23，46，31，0，13）、时间是5 s，第三个路径点为（41，21，52，20，15，26）、时 间是 4 s，终止点为（60，31，62，31，36，30）、时间是3 s。用该算法时，服务机械臂各关节速度时间曲线如图8所示。

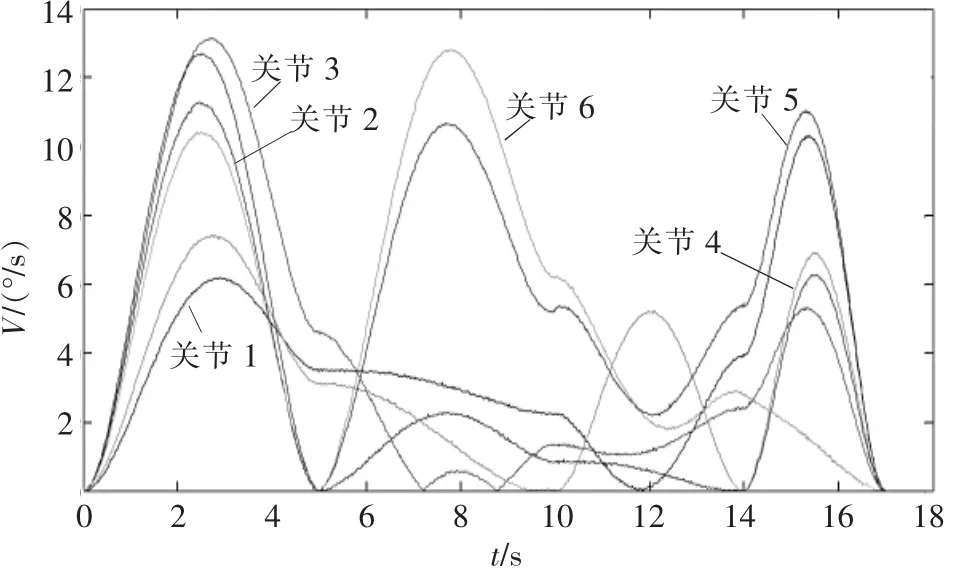
▲图8 过路径点五次多项式插值V-T图

由图8可知，过路径点五次多项式插值算法能实现过路径点连续运动，而且路径点连接处速度、加速度连续，整个运动过程振荡极小。

2.5 直角坐标路径控制法实现直线运动

为实现服务机械臂末端的直线运动，轨迹规划器实现了直角坐标路径控制插值算法，采用抛物线过渡离散规则，根据指令系统传入目标位姿、位置运动速度、姿态运动速度、运动时间，利用四元数进行位姿离散。设当前位姿为P0，目标位姿为P1，位置直线运动速度为V1，运动时间为T，则：

（1）根据当前位置P0=（x0，y0，z0）、目标位置P1=（x1，y1，z1）、直线运动速度V1和运动时间T，按照抛物线过渡运动，计算出从初始位姿P0直线插值运动到P1的位置直线运动加速度A1：

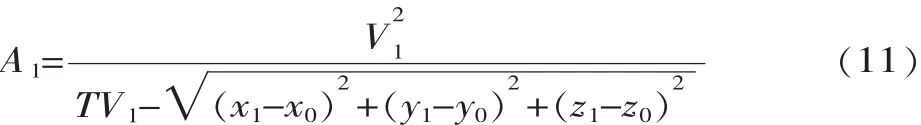
（2）由姿态矩阵R0和目标姿态矩阵R1，计算出两姿态矩阵对应的四元数，然后利用四元数的共轭性质求解出，利用四元数乘法性质计算出工具姿态由R0转为R1的姿态旋转矩阵R为：

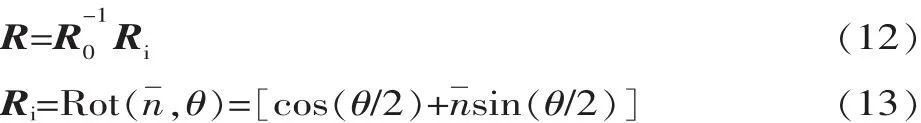
最后将姿态旋转矩阵R，利用旋转变换式（13），计算出等效旋转轴n的等效旋转角度θ。

（3）由上步计算得等效旋转角度θ，根据抛物线过

渡运动，计算出姿态运动速度V2和加速度A2，即：

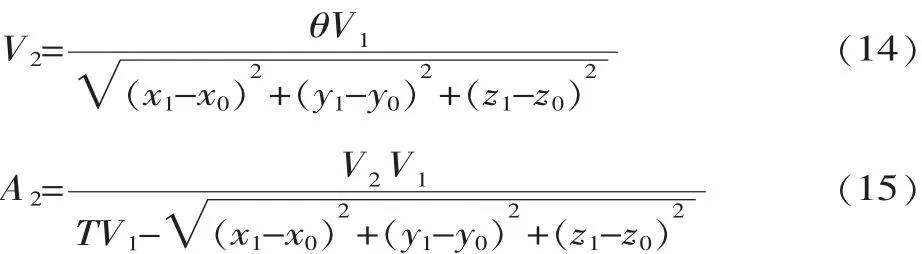
（4）根据计算出来的抛物线过渡参数，采用抛物线过渡法计算离散位姿。

（5）用运动学求解器求解出各离散位姿对应的关节位置。

（6）采用过路径点五次多项式插值算法，控制服务机械臂和仿真模型按离散关节位置实现过路径点的连续运动，实现直线运动轨迹。

以悬挂六自由度服务机械臂为例进行实验，设：初始位姿为 （-190，25，-500，0，180，0），末端位姿为（-70，25，-500，0，120，0），位置运动速度为20 mm/s，运动时间为8 s，用该算法规划时，服务机械臂末端运动轨迹如图9所示，与理想位置比较所得偏差如图10所示。

由图10可以看出，各采样点3个方向的目标位置与理想位置的偏差都在2.5 mm范围内，则直线位置最大偏差为4.33 mm。由图9可知，服务机械臂走出一条较精准直线，但该算法无法显示设定直线精度。

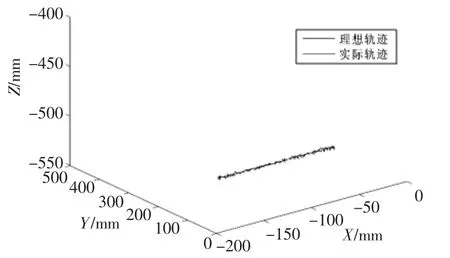
▲图9 直角坐标控制法末端轨迹

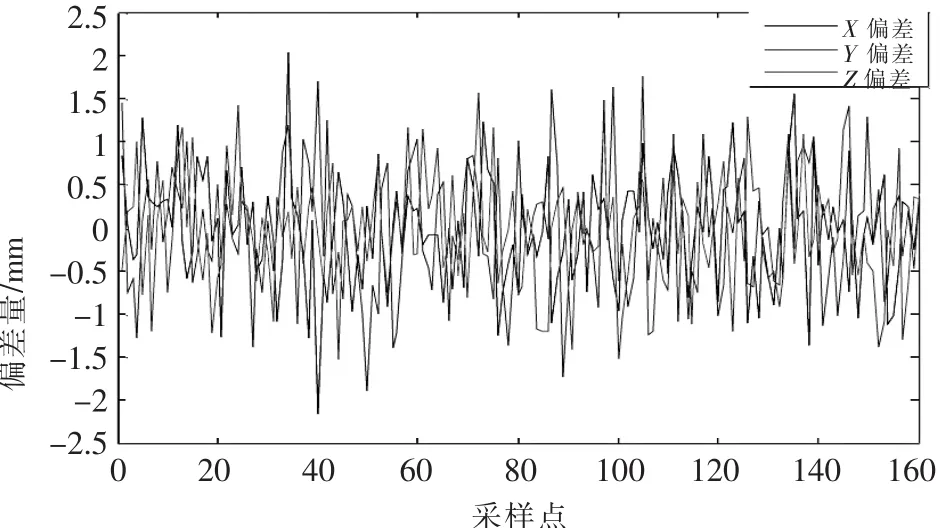
▲图10 末端轨迹偏差

3 基于BDJP法轨迹规划

3.1 BDJP法实现直线运动

为克服直线精度无法设定问题，笔者采用了BDJP（Bounded Deviation Joint Path）法实现直线插值。设：起始位姿为P0，末端位姿为P1，运动时间为T，位置最大偏差为δp，旋转最大偏差为δR，其具体步骤如下。

（1）计算关节变量解，计算对应于P0和P1的关节矢量q0和q1。

（2）求出关节空间的中间点，计算关节变量空间的中间点：

式（16）中，Δq1=q1-q0，再由qm计算相应的工具坐标系Pm。

（3）求出直角坐标空间的中点，计算相应的直角坐标路径的中点PC：

（4）求出偏离误差，计算Pm和PC之间的偏差：

（6）根据总时间T和插值最大位移，将总时间进行细分。

（7）然后按照过路径点五次多项式插值算法，进行关节插值控制。

以悬挂六自由度服务机械臂为例进行实验，设：初始位姿为 （-190，25，-500，0，180，0），末端位姿为（-70，25，-500，0，120，0），位置最大偏差为2 mm，最大旋转偏差为3°，运动时间为10 s，用该算法规划时，服务机械臂末端运动轨迹如图11所示，与理想位置比较所得偏差如图12所示。

由图12可知，采用BDJP法实现轨迹规划时，各采样点3个方向的目标位置与理想位置的偏差都在1.1 mm范围内，则直线位置最大偏差为1.91 mm，满足2 mm的设定要求。由图11可知，该算法能够实现可控制精度的直线插值。

3.2 BDJP法实现圆弧运动

在BDJP直线插补算法的基础上，实现末端轨迹圆弧插值，基本思想是首先根据指令系统指定的圆弧中间点位姿、圆弧终点位姿计算出圆弧中心和圆弧半径；然后再根据最大位置精度计算出细分弧，如图13所示，获得细分点位姿；然后计算出圆弧在精度内细分

的各个点，再按照BDJP法直线插值算法代替圆弧进行插值运动控制。

以悬挂六自由度服务机械臂为例，设：圆弧初始位姿为（-20，0，-750，0，180，0），中间点位姿为（-120，-100，-750，0，180，0），圆弧终点位姿为（-220，0，-750，0，180，0），位置最大偏差为2 mm，旋转最大偏差为3°，T为13 s，用该算法规划时，服务机械臂末端运动轨迹如图14所示，与理想位置比较所得偏差如图15所示。

由图14可知，服务机械臂按照该算法能够实现圆弧轨迹插值运动，而且由图15可知，各方向最大偏差值都小于1.5 mm，圆弧位置偏差最大小于2 mm，满足算法设定精度。

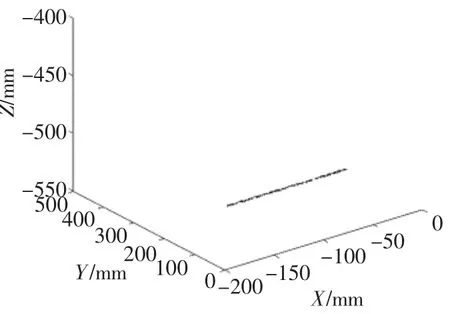
▲图11 BDJP法末端轨迹

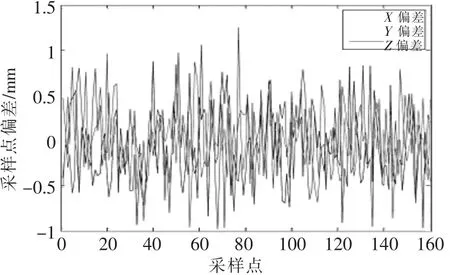
▲图12 末端轨迹偏差

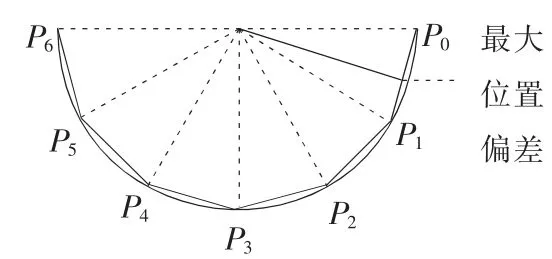
▲图13 圆弧细分作直线处理方法

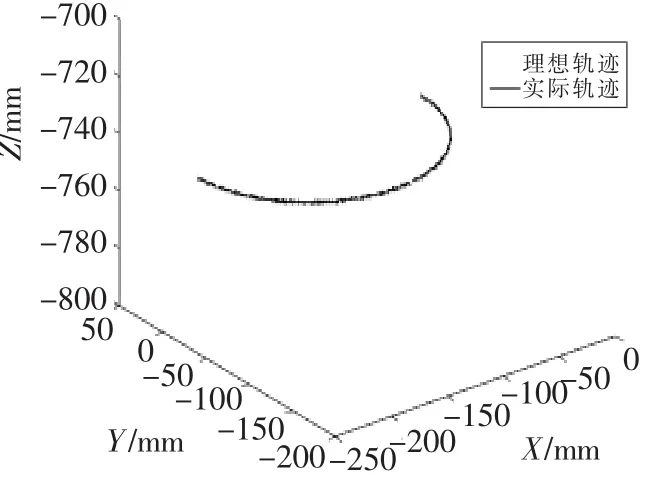
▲图14 圆弧插值实验末端轨迹

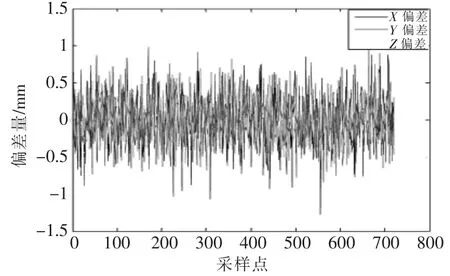
▲图15 末端轨迹偏差

4 机械臂轨迹规划实验

该平台已完成多种配置模块化服务机械臂的同步在线控制测试，以竖直六自由度服务机械臂进行在线模型控制实验为例，其测试如图16所示。

为测定BDJP直线插补算法，用直线指令LINE，设：位置插值误差为5 mm，旋转插值误差为1°，编写指令文件，完成服务机械臂走“中”字的实验，如图17所示。

为验证BDJP圆弧插补算法，用圆弧指令CIR3P指令，设：位置偏差为5 mm，旋转偏差为1°，编写指令文件，完成悬挂六自由度服务机械臂走圆实验，如图18所示。

经过多次实验，算法的稳定性、可靠性得到了检验，平台的功能和性能也得到了完善和提高，验证了仿真控制平台在模块化服务机器人的模型构建、仿真控制、在线同步控制以及轨迹规划、指令控制等方面的功能。

▲图16 竖直六自由度机械臂同步在线测试

5 结论

本文以Schunk模块化服务机器人为研究对象，基于BDJP插值算法完成了服务机器人的轨迹规划工作，完成模块化服务机器人仿真控制平台的搭建。在该仿真平台上，完成了在线同步测试、悬挂六自由度服务机械臂走 “中”字和走圆实验，验证了平台的功能和性能。

作为模块化机器人仿真控制平台，本文的研究工作在实时性、场景精细等方面还存在较多不足，整个仿真控制软件主要从服务机械臂的建模和运动控制出发，未考虑服务机械臂的工作环境、手臂受

力情况等因素，下一步将考虑把增加服务机械臂作业环境的建模作为后续研究内容，并考虑把实现服务机械臂运动过程中各模块受力情况的仿真分析作为研究重点。另外，设计的服务机械臂运动学求解器还具有一定的局限性，不能够适应建立的所有模型。下一步将考虑从服务机械臂机构学的角度分析其运动学求解过程，建立具有普遍适应性的统一运动学求解算法。最后，设计的轨迹规划器实现的轨迹规划算法还非常有限，下一步将考虑研究具有避障、指定任务轨迹自动生成等更加高级的轨迹规划算法。

▲图17 走"中"字实验

▲图18 走圆实验

［1］姚玉峰，苏衍宇，黄博.面向服务机械臂有效操作特征提取的示教方法［J］.机械工程学报，2013，49（3）：10-17.

［2］高美真.OpenGL在基于图形建模技术中的应用［J］.现代计算机，2005（12）：92-94.

［3］伍文伟，朱志杰，伍良伟.一种基于Lab Windows/CVI和OpenGL的六自由度机械手三维建模的方法［J］.电子测量技术，2007，30（8）：75-77.

［4］李宪华，郭永存，郭帅，等.基于CAN总线结构的服务机器人模块化双臂系统构建 ［J］.机床与液压，2013，41（17）：22-23.

［5］赵建文，杜志江，孙立宁. 7自由度冗余手臂的自运动流形［J］.机械工程学报，2007，43（9）：132-137.

［6］封文春，林贵平.四元数在弹射座椅性能仿真中的应用［J］.北京航空航天大学学报，2006，32（8）：881-884.

［7］李宪华，郭永存，张军，等.模块化六自由度机械臂逆运动学解算与验证［J］.农业机械学报，2013，44（4）：246-251.

［8］孙亮，马江，阮晓钢.六自由度机械臂轨迹规划与仿真研究［J］.控制工程，2010，17（3）：388-392.

［9］熊有伦.机器人技术基础［M］.武汉：华中科技大学出版社，2008.

［10］张小江，高秀华.三次样条插值在机器人轨迹规划应用中的改进研究［J］.机械设计与制造，2012（9）：170-171.

［11］刘鹏，宋涛，贠超，等.焊接机器人运动学分析及轨迹规划研究［J］.机电工程，2013，30（4）：390-394.

［12］Kubota N，Arakawa T.Trajectory Generation for Redundant Manipulator Using Virus Evolutionary Genetic Algorithm.［C］Robotics and Automation，1997 Proceedings，IEEE International Conference,Albuquerque USA，1997.

［13］刘鹏飞，杨孟兴，宋科，等.‘S’型加减速曲线在机器人轨迹插补算法中的应用研究［J］.制造业自动化，2012，（20）：4-11.

［14］R H Taylor.The Planning and Execution of Straight Line Manipulator Trajectories［J］.IBM Journal of Research and Develapment，1979，23（4）：424-426.

［15］栾海英，刘学君.基于CANopen协议绝对值光电编码器的伺服位置控制的研究［J］.制造业自动化，2013,35（9）：151-153.

［16］卓扬娃，白晓灿，陈永明.机器人的三种规则曲线插补算法［J］.装备制造技术，2009（11）：27-29.

（编辑 丁 罡）

TH122；TP242.6

A

1000-4998（2015）10-0011-07

*上海市科学技术委员会科技支撑项目（编号：14111104502）

2015年3月