基于能量释放率的Ⅱ型裂纹开裂分析

蔡永梅， 张芳瑶， 谢禹钧

(辽宁石油化工大学机械工程学院，辽宁抚顺 113001)



基于能量释放率的Ⅱ型裂纹开裂分析

蔡永梅， 张芳瑶， 谢禹钧

(辽宁石油化工大学机械工程学院，辽宁抚顺 113001)

分叉开裂问题是一个新型的断裂力学问题，本文利用经典Ji-积分守恒律，对部分路径积分，分析Ⅱ型裂纹分叉开裂时能量释放率，并指出裂纹边界分叉开裂的应力强度因子与Ji-积分的关系。当裂尖奇异应力场的应力集中达到一定程度时，即达到临界条件时，该应力场所在的边界将开裂，通过边界移动的能量释放率的分析定量地给出了边界分叉开裂能量释放率数学表征及边界开裂的极限临界载荷。

断裂韧性；Ji-积分； 裂纹分叉； 应力强度因子； 临界载荷

裂纹折裂和分叉问题的研究起源于裂纹高速动态扩展，后来发现扩展速度较低时也有裂纹分叉的现象，也有实验表明裂纹的准静态扩展也有分叉问题。裂纹扩展过程非常复杂，预测裂纹扩展方向仍然存在很大的挑战性，部分是由于裂纹扩展具有多级分叉现象。事实上，这一复杂问题需要进一步简化，即使对于各向同性材料，开裂机理取决于裂纹开裂形式和所承受载荷类型。Clark和Irwin、Schardin等认为应当用临界应力强度因子KIC或应变能释放率G描述裂纹的分叉，而不是用裂纹高速扩展引起的应力分布的变化检验裂纹是否分叉[1-3]。

这一认识在一定的程度上重新确认了应力强度因子K或应变能释放率G在描述裂纹分叉分析中的地位和作用。然而，这些观点没有受到应有的重视和研究。本课题的研究将在理论上验证Clark和Irwin、Schardin提出的观点。

裂纹分叉研究在理论上和工程应用上具有重要的意义。首先可以揭示裂纹的完整扩展规律，对完善和丰富断裂力学理论体系有积极的贡献。在工程应用上裂纹的分叉会促成多个裂纹尖点的产生，客观上导致各裂纹尖端的应力强度因子骤降，应力集中程度受到很大程度的削弱，达到止裂的目的，能有效阻止工程构件的灾难性断裂，具有优良的工程应用价值。

1 边界开裂的断裂韧性

对于均质、各向同性材质的弹性实体，其边界开裂的最大能量释放率为：

(1)

其中vi表示 “速度”；mi是边界s上的外向单位法矢量，w为应变能密度。

如果令vi=ei=Δi/Δ表示单位位移在坐标方向上的分量，即e1=cosα, e2=sinβ，α为位移Δ与x1的夹角，β为位移Δ与x2的夹角。若引进ni=-mi表示路径s内法线单位向量，即代表边界向弹性体内部方向移动[4-5]。于是边界移动的能量释放率可定义为：

(2)

如果边界s上的各点均以同一个方向运动，边界开裂二维模型如图1所示，则式(2)可由守恒积分Ji表示，即:

(3)

图1 s→0时边界开裂二维实体模型

Fig.1 Model of boundary cracking whens→0 for two-dimensional solids

在数学和几何上，边界的开裂等价于边界的移动。局部边界s几何移动后形成一个缺口，当s→0后缺口退化成裂纹，构成了边界单裂纹开裂的几何模型。前期的研究工作表明[6-7]，其自由边界s沿α(与x1方向的夹角)方向开裂的能量释放率为：

(4)

其中

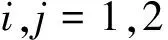
(5)

其中sl为弹性体内任意一条积分曲线，且与s构成闭合回路。其中(J1)|s→0为边界s沿x1方向单位移动的能量释放率，即能量型驱动力；(J2)|s→0为边界s沿x2方向单位移动的能量型驱动力。通过研究该模型不仅适用于裂纹问题，也适用于压痕边界等一般边界的开裂问题。

2 Ⅱ型裂纹Ji-积分

考虑弹性体裂纹面，泊松比μ，弹性模量E。分析中采用局部直角坐标系x1，x2。同时引入柱坐标系统(r，θ，z)，其与直角坐标关系为x1=rcosθ，x2=rsinθ。裂尖局部边界示意如图2所示，积分路径Г从裂纹下表面到上表面，假定裂纹表面自由，在其他边界上的载荷或位移沿着裂纹面平行或者正交方向[8-10]，从而更好地分析所提出的问题。

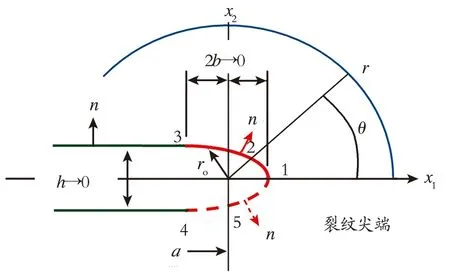
图2 裂尖局部边界(ro→0+)

Fig.2 The local boundary of the crack tip (ro→0+)

参考图2所示的坐标系统，其中x1垂直于裂尖，x2垂直于裂纹面，将线弹性断裂力学中裂尖的应力和位移场代入方程(5)中，由式(5)得出：

(6)

(7)

(8)

(9)

KⅡ为滑开型裂纹应力强度因子。也意味着应力强度因子能够通过Ji-积分来计算，即沿着裂纹下表面任意一点到上表面任一点的积分路径来计算Ji-积分从而得出K值[11-12]。

3 Ⅱ型裂纹边界分叉式开裂分析

3.1 裂尖处Ji积分基本特征

在Ⅱ型裂纹裂尖处存在K-控制区，裂尖处积分路径如图2所示。J1-积分在裂尖边界附近所处的四个象限均为正。J2-积分在Ⅰ 和 Ⅲ 象限为正值，在Ⅱ和Ⅳ象限为负值。当h→0并且b→0，裂尖边界区域分为四部分，裂纹边界为：s=s45+s51+s12+s23→0，在各象限内分别给出能量释放率以便于分析裂尖的分叉行为。以Js23-积分为例，利用方程(6)和(7)得出Ji-积分：

(10)

(11)

应用同一方法得出沿路径s12、s23、s45和s51上的Ji-积分值，如表1所示，正则化的沿积分路径各Ji-积分变化如图3所示，取μ=0.3分析。

表1 沿路经s12、s23、s45、s51 和正则化Ji-积分

图3 沿积分路径 Ji-积分分布规律

Fig.3 Along the integration pathJi- integral distribution rule

3.2 Ⅱ型裂纹开裂能量释放率

J1(s12)、J1(s23)、J1(s45)和J1(s51)均为正值，如表1所示，意味着它们对裂纹边界扩展及裂纹边界沿着x1方向扩展起作用。J2有着不同的行为，J2(s12)>0 表明如果边界s12沿着x2方向扩展，裂纹体将释放能量，须考虑该积分对裂纹扩展的影响。J2(s23)<0意味着边界s23沿着x2负方向移动，裂纹体将吸收能量，这是不可能发生，因此，这种情况下的将不考虑J2(s23)的影响。然而-J2(s51)>0 意味着边界沿着x2负方向移动，意味着如果边界s51沿着x2负方向移动，裂纹体将释放应变能，则必须考虑该积分对多级裂纹分叉扩展的影响。同理，在-J2(s45)<0这种情况下，实际中它也是不可能发生的，也不考虑-J2(s45)的影响。

由以上分析，不难得出裂纹分叉的能量释放率，裂尖边界能量释放率分别表示为：

(12)

(13)

(14)

(15)

可由方程(4)获得不同开裂形式的能量释放率，例如准静态三叉开裂裂纹能量释放率：

(16)

将表1中的结果带入式(16)可得到如下结果：

(17)

(18)

(19)

其中α1c和α2c是理论推导的可能产生的临界开裂角，Gtri-b为三叉开裂时的最大应变能，可用修正因子Ftri-b来表示该最大应变能为：

(20)

式中:

(21)

当三叉开裂时最大应变能(Gtri-b)max趋近于临界应变能时，Ⅱ型裂纹在裂纹扩展时将沿着三角形分叉，疲劳测试中也得出相应的现象，并且很显然属于支裂纹增长。

4 结论

文中给出了一个裂纹分叉开裂的研究方法，将部分路径积分与能量释放率结合起来，建立了裂纹分叉开裂的能量释放率，导出了临界开裂条件。并指出裂纹边界分叉开裂的应力强度因子与Ji-积分的关系。同时，也证明Griffith理论不仅适用于裂纹扩展也适用于裂纹分叉。

[1] Clark A B, Irwin G R. Crack-propagation behaviours[J]. Experimental Mechanics, 1966, 6:321-330.

[2] Cotterell B, Rice J R. Slightly curved or kinked cracks[J]. International Journal of Fracture, 1980, 16:155-169.

[3] Budiansky B, Rice J R. Conservation laws and energy-release rates[J]. Journal of Applied Mechanics, 1973, 40:201-203.

[4] Sumi Y, Nemat-Nasser. On crack path stability in a finite body[J]. Engineering Fracture Mechanics, 1985, 22:759-771.

[5] Zeng R, Wang M O. Branching extension characteristics of mode-II crack under fatigue loading[J]. Engineering Fracture Mechanics，1994, 49:487-498.

[6] 王晓华，蔡永梅，谢禹钧.平板双侧触压的应力强度因子[J].工程力学，2009, 26(3):6-8.

Wang Xiaohua, Cai Yongmei, Xie Yujun. Stress intensity factor of a panel under double-side indentations[J]. Engineering Mechanics, 2009, 26(3):6-8.

[7] 蔡永梅，谢禹钧.平板双侧刚性压头对压的开裂分析[J].工程力学，2012,29(2):235-238.

Cai Yongmei, Xie Yujun. Cracked analysis for panel under indentations[J]. Engineering Mechanics, 2012,29(2):235-238.

[8] Xu X P. Numerical simulations of fast crack growth in brittle solids[J]. Journal of the Mechanics and Physics of Solids, 1994, 42:1397-1434.

[9] Xie Y J, Cai Y M. Applications of conservation integral to indentation with a rigid punch[J]. Engineering Fracture Mechanics, 2009, 76:949-957.

[10] Xie Y J, Wang X H. Stress intensity factors for cracked homogeneous and composite multi-channel beams[J]. International Journal of Solids and Structures, 2007, 44:4830-4844.

[11] Xie Y J. An analytical method on circumferential periodic cracked pipes and shells[J]. International Journal of Solids and Structures, 2000, 37:5189-5201.

[12] 蔡永梅，王伟，谢禹钧.不同基体平面压痕应力强度因子[J].石油化工高等学校学报，2012,25(4):77-80.

Cai Yongmei, Wang Wei, Xie Yujun. SIF for different panel under indentations[J]. Journal of Petrochemical Universities, 2012, 25(4):77-80.

(编辑 王亚新)

An Energy-Based Fracture Model for Cracking from Mode-Ⅱ Crack-Tip

Cai Yongmei， Zhang Fangyao， Xie Yujun

(School of Mechanical Engineering, Liaoning Shihua University, Fushun Liaoning 113001, China)

The cracking branching is a new type of fracture problem. The classicJi-integral has been further explored utilizing a partial integral path, from which an analytical solution of the energy release rate for mode-Ⅱcrack-branching. The SIFs is determined for the crack based on theJi-integral. When the singular stress field reaches its critical value, fracture will take place on the surface of boundary. The fracture of crack-branching is formulized and the critical load also is analytically derived by using the energy release rate of boundary translation.

Fracture toughness;Ji-Integral; Crack-branching; Stress intensity factors; Critical load

1006-396X(2015)05-0095-04

2014-06-30

2015-05-20

国家自然科学基金项目(50771052，50971068)；辽宁省自然基金项目(20082188)；辽宁省教育厅重点实验室项目(LS2010100)。

蔡永梅(1981-)，女，博士研究生，讲师，从事断裂力学、化工机械等研究；E-mail:cymlnpu@163.com。

谢禹钧(1960-)，男，博士，教授，博士生导师，从事断裂力学、结构完整性评定等研究；E-mail:yjxie@mail.fsptt.ln.cn。

TE905; O346.1

A

10.3969/j.issn.1006-396X.2015.05.019