学习《大学物理》的两个难点

韦芳萍沈路名

（1.广西大学物理科学与工程技术学院，广西 南宁 530004；2.钦州市三中，广西 钦州 535000）

学习《大学物理》的两个难点

韦芳萍1沈路名2

（1.广西大学物理科学与工程技术学院，广西 南宁 530004；2.钦州市三中，广西 钦州 535000）

《大学物理》是大学课程中一门非常重要的基础课。学习大学物理有两个难点：一是如何掌握微积分在物理中的应用；二是矢量和矢量的计算在物理中的应用。文章对两个难点进行了介绍和引导，给学生学习大学物理提供一些建议和参考。

微积分；矢量；大学物理

大学物理课程是理工科学生学习专业课必要的物理基础，同时还是培养学生现代的科学自然观、宇宙观和辩证唯物主义世界观，培养他们的探索、创新精神和科学思维能力，掌握科学方法的一门很重要的课程，其作用是其他课程不能代替的。大学物理中有很多知识是对中学物理的延伸和扩张，但又不是中学物理内容的简单增加和提高。

笔者有多年的《大学物理》教学经验。在教学过程中，经常发现学生对《大学物理》有非常大的误解，以至于学不好《大学物理》。误解一：认为大学物理其实和高中物理知识差不多，不用多费时间，用高中知识也可以解决大学物理中的问题；误解二：认为大学物理与数学无关，数学学不学都可以学好大学物理。持有以上错误观点的同学上完大学物理课程后，大部分的同学都要挂科。

大学物理课程对学生来讲一方面觉得很熟悉，因为大部分知识在高中阶段已学过，另一方面又觉得它太难学了，就像有的学生说“物理课我听懂了，但就是不会做题”。很多学生学习兴趣不浓，学习效果较差，究其原因在于，跳不出高中阶段的思维模式，不能用科学的思维方法和研究方法处理较为复杂的问题，特别是不善于利用高等数学的微积分知识处理较为复杂的物理问题。大学物理教材的内容虽然也是力学、热学、电磁学、光学和原子物理五部分，但是在深度和广度上都有加深和拓展，而且，与高等数学知识的结合比较紧密，大学物理中要用到高等数学知识，有许多内容学生在高等数学课还没学过或还没学好，学生还必须学会如何使用高等数学的问题，所以难度增加了[1-3]。

《大学物理》对于理工科学生来说，难点集中在以下两点：微积分在物理中的应用；矢量。

1 微积分在物理中的应用

微积分的基本思想是什么？是无限细分和无限求和[4]。历史上，微积分被称为无穷小分析或无穷小代数。微元分析法：就是无穷小求和的方法。要学好大学物理，如何掌握微积分在物理中的应用即掌握微元分析法是一个难点。如何从高中的平均值计算过度到无限小计算呢？这必须从函数说起，

对于y=f(x)如果当自变量x无限趋近(数学有严格定义[ε,δ])某一数值(记作x→x0)时，函数f(x)的数值无限趋近某一确定数值a,则a叫做x→x0时函数f(x)的极限值或f(x)的极限等于a[5]，记作

如

讨论当x→1时极限，结果为5:

将此结果及时引导到物理中，如

或选任一时刻t，vt=v0+at

通过这样的分析和引导，高中物理中的匀加速运动的求平均速度的问题就过渡到了求瞬时速度的问题。

从极限问题再过渡到微分问题就非常的容易接受：

变量的增量：

函数增量:

增量之比:

记为

还记为:

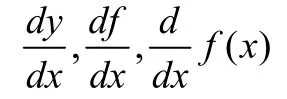
通常把自变量x的增量▽x称为自变量的微分，记为dx，即 dx=▽x。即函数的微分与自变量的微分之商等于该函数的导数,即：

攻克微分在物理中的应用，还必须强调微积分的观点，如何巧取“微元”，是提高运用微积分知识解决较复杂物理问题的能力的关键。下面举例说明如何巧取“微元”，并利用微积分的知识解决几类较为复杂的物理问题。例如：求变力做功

功表示力对空间的积累作用。恒力作用在物体上，物体作直线运动时恒力所做功

图1 力F做功

如果变力作用在物体上，物体作曲线运动，可以应用微积分的知识进行计算。将物体运动的轨迹分成无数个小的微元，变力在无限小过程中的元功dA—F·dr，那么变力在某一位移中的功。如求质点M 在变力作用下，沿曲线轨迹由a 运动到b，变力作的功，在一段上的功：

图2 变力做功

由此将微积分应用到了物理问题中。

2 矢量和矢量计算在物理中的应用

矢量可以说是学习《大学物理》的第二个难点。很多学生学习完大学物理之后仍然不明白为什么大学物理中要引入矢量。大学物理中的物理两有两种性质，一种是矢量性，另外一种是标量性。矢量亦称“向量”。有些物理量，是由数值大小和方向才能完全确定的物理量，这些量之间的运算并不遵循一般的代数法则，在相加减时它们遵从几何运算法则，这样的量叫“物理矢量[6]”。如速度、加速度、位移、力、冲量、动量、电场强度、磁场强度……等都是矢量。可用黑体字（例如F）或带箭头的字母来表示。标量亦称“无向量”。有些物理量，只具有数值大小，而没有方向。这些量之间的运算遵循一般的代数法则。这样的量叫做“标量”。如质量、密度、温度、功、能量、路程、速率、体积、时间、热量、电阻等物理量。无论选取什么坐标系，标量的数值恒保持不变。矢量和标量的乘积仍为矢量。矢量和矢量的乘积，可构成新的标量，也可构成新的矢量，构成标量的乘积叫标积；构成矢量的乘积叫矢积。如功、功率等的计算是采用两个矢量的标积。对初学大学物理者，矢量与矢量计算是难点中的难点。习惯了代数量的运算，矢量运算总感到不习惯。大学物理中有许多物理量是矢量，只有对矢量充分认识和熟练应用矢量计算，才能解决一些疑难问题，而矢量的表示和运算必须建立在一定坐标系的基础上，因此对各种坐标表示必须熟练掌握[7]。如求质点的加速度可以用直角坐标表示为：

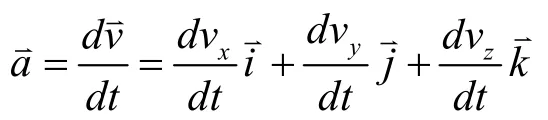
也可用自然坐标表示，用这种方法，质点运动的加速度物理意义更明确。设在t时刻，质点经过A点，速度为，其指向在轨道A点的切线上，经过一段时问后，质点经过B点，速度为⇀ + Δ⇀，其指向在轨道B点切线上。如图3(a)。根据矢量计算，画出矢量图，如图3(b)所示，将分解为→和，为速度方向变化引起的速度增量，为速度大小变化引起的速度增量，即：

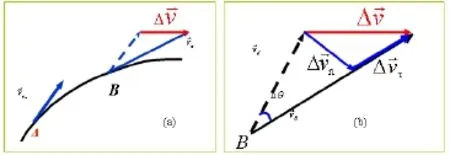
图3 速度改变量矢量分解图

那么

是由于速度方向变化引起的法向加速度，a，是由于速度大小变化引起的切向加速度。可见，利用自然坐标发表示加速度更为方便实用。初学者应对各种矢量表示法熟练掌握，根据问题需要将矢量表示为不同形式。

矢量的计算在物理学中的应用比较难的是矢量的点乘。物理学中的点积即两个矢量相乘，其实就是一个矢量在令一个矢量的模乘以另一个模，再乘以它们的夹角的余弦值。物理意义就是一个矢量在另一个矢量上的投影大小。投影值再和另一个矢量相乘。这是因为，有时物理中有时要求两个相乘的量必须在一个方向上。比如 ，做功，是力矢量与距离矢量的乘积，做功要求可以是力和使物体产生的距离在同一方向上。这时，就要力投影到距离方向上，或距离投影到力矢量方向上，总之，方向要一致。这时，矢量的乘积运算正是这种，两项的值在同一方向上的乘积。由于投影只是乘以夹角的余弦值，两个矢量的夹角固定，所以，向哪个方向投影只是解释的不同，但运算结果是一样的。同时，在直角坐标系中，还可以将力分解到各个分坐标轴上，合力的功等于各个分力做功的总和。即

最终将矢量计算变成了标量。

3 结语

综上所述，只要在学习《大学物理》的过程中注意微积分和矢量的应用，这两个难点将会很容易克服。教师在教学中注意突出微积分的观念，教学生如何利用无限小微元分析法，将会使学生逐渐接受和适应微积分在物理中的应用；同时在教学中还要突出矢量的重要性，把物理问题和数学问题相结合起来，将会受到良好的教学效果。

[1]赵兴华.大学物理和中学物理的区别[J].中国科技信息, 2005,2(22):144-145.

[2]王绿波.浅谈物理教学实验及能力培养[J].科教文汇, 2011,(1):95-96.

[3]刘亚慧,张桂梅.大学物理和中学物理教学的差别[J].新课程研究(职业教育),2008,(126):123-124.

[4]刘培姣,徐志立.突出“微元”积分观念是学好《大学物理学》的关键[J].高等函授学报(自然科学版),2007,20(2): 30-32.

[5]同济大学数学系编.高等数学(第六版)[M].高等教育出版社,2007:2-9.

[6]程学勤.《大学物理》教材中矢量方法的运用[J].华中师范大学学报,1987,21(3):475-480.

[7]徐灿,袁铃,尹钊.矢量分析在物理规律中的应用[J].高师理科学刊,2011,32(1):59-62.

Two difficulties of learning college physics

The College physics is an important basic course of university curriculum. There are two difficulties of learning college physics. One is how to master calculus in the application of physics; the second is vector and vector calculation in the application of physics. This paper introduces the two difficulties and guidance to give some Suggestions and reference for the students learning college physics.

Infinitesimal calculus; vector; college physics

G64

A

1008-1151(2015)05-0138-03