某型号收割机割刀机构及其传动部件惯性力平衡的研究*

许汝炜，王俊田

(1．西华大学机械工程与自动化学院，四川成都 610039;2．淮北矿业(集团)有限责任公司桃园煤矿，安徽宿州 234116)

0 引言

机械构件在没有进行过惯性力平衡的前提下运转时，会产生相应的惯性力，而这种惯性力会在运动副中产生相应的动压力。这不仅会增加运动副中的摩擦和构件中的内应力，降低机械效率和使用寿命，而且由于这些惯性力一般都是呈周期性变化的，所以必将引起构件基座以及构件相关联的机械设备产生强迫振动。强迫振动对机械本身的危害性很大，如其振动频率接近或与机械的固有频率一致的话，不仅会使机械性能大大下降而且会给机械本身带来破坏性的重创［1］。因而为了适应机械高速化和精密话的发展趋势必须降低机械惯性力所带来的不利影响。

收割机在收割农作物时，割刀运动副来回运转会产生很大的呈周期性变化的惯性力作用于割台机架上，这将会对机架或其它零部件产生激励，引发较强的振动和噪音，影响收割机的工作精度、可靠性和寿命。尤其当割刀及割刀传动机构的产生激振力的频率接近机架的固有频率时，会对割台及收割机其它部件产生极大的破坏作用。因此要尽可能的减小其惯性力的影响。但是在做机构惯性力平衡时，做到机构惯性力为零或者最小时，所需的配重质量往往过大，很多时候要大于机构自身的质量。其次在安装这些配重时，由于配重本身及安装位置对空间上的需求往往给机构周围的零部件带来很严重的干涉。因此考虑多目标优化函数，采取部分平衡就体现出更大的价值。在本收割机的割台上受于割台本身的尺寸及收割机性能等的多方面限制，要达到完全平衡或者惯性力最小的情况也许是不可能的，在此分完全平衡和最优平衡两种角度进行研究，然后在对其进行比对从中选取最优的方案进行总结，为类似的机构研究提供参考。

1 该机构工作原理及惯性力分析

1．1 割刀机构及其传动构件的工作原理

如机械运动简图1所示，动力从A点输入带动曲柄AB做匀速圆周运动，摇杆CDE跟随连杆BC的联动，从而做相应的摇摆动作。在通过凸轮机构E和一个移动副F，使得割刀把摇杆的摇摆动作转换成割刀的来回往复的循环运动，从而切割农作物。从该运动简图中不难看出该机构是由一个曲柄摇杆机构、一个凸轮机构以及一个移动副机构组成的六杆机构。

在分析该机构整体的惯性力时，发现割刀F处是由移动副所包围的。在机械动力学中我们知道，被移动副所包围的机构是不能够通过增减配重的方法进行机构惯性力完全平衡处理的。因此只是通过增减配重该机构是不能够进行惯性力完全平衡的，只能够把机构整的体惯性力大小降到最低点［2］。

1．2 惯性力分析计算和比较

采用机构运动解析法对机构进行分析。先拿出该机构各个杆件质心的运动位移方程，对其位移方程进行求导得出其质心的速度方程，再根据微分思想及牛顿第二定律，借用Matlab计算软件进行数值计算，得出该机构一个周期内的机构惯性力的变化情况。

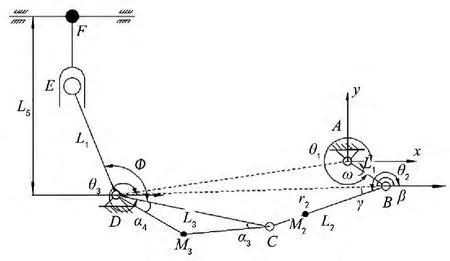
图1 割刀及其传动构件的机械运动简图

如图1所示在割刀及其割刀的传动构件的机构运动简图上建立固定坐标系yAx。A点和D点均为铰链支点。已知参数为:曲柄转速ω=1002 rad/min，曲柄半径 L1=25 mm，曲柄质量 M1=2．6838 kg，其质心相对于极坐标的位置为:R1=0．23 mm，α1=11°。连杆长度 L2=177 mm，质量 M2=0．9698 kg，质心相对极坐标为:R2=80 mm，α2=0。摇杆长度L3=111．48 mm，L4=110．95 mm，L3和 L4之间的夹角 φ=146．1°，质量为 M3=2．6976 kg;其质心相对极坐标的位置为:R3=73．47 mm，α3=24．91°，R4=53．7 mm，α4=45．1°。滑动杆参数 L5=153．75 mm，(为滑动杆到固定铰链D点的距离)，D点坐标为:(-220，-32)'，M4=2．3862 kg，R5=236．6 mm。

通过运动解析法建立其数学模型的递推表达式如下:

B点的矢量方程为:

B→=L1×［cos θ1，sin θ1］T

为得到C点的矢量方程我们通过建立辅助三角形ΔBDC逐步求得:

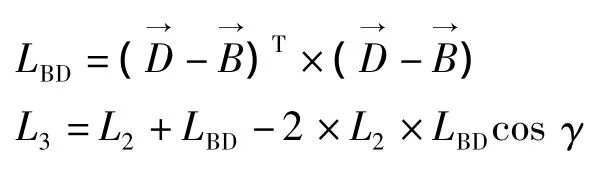
得到:

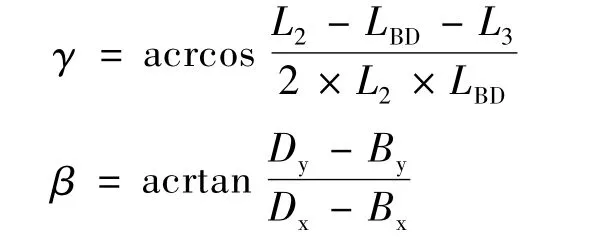
从而得到θ2为:

θ2=β+γ

由此得到C点的矢量方程为:

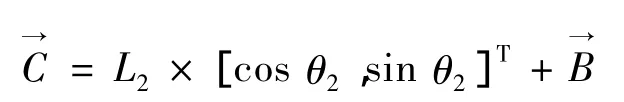
依次推导θ3得:

由此就得到E点和F点的位置方程:

由以上的位置矢量方程得其对应的质心方程分别为:

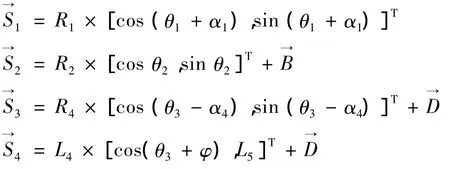
在知道这些点的位置函数之后，我们利用微分思想，取时间间隔很短，逐次求各个质心位置的速度加速度，结合牛顿第二定律在运用Matlab强大的计算功能对其进行编程求解，计算出原某型号收割机割刀及其传动部件的惯性力结果如图2所示。

通过Matlab的计算我们得到，原收割机该机构的惯性力峰值是8．0 N，从机构模型上也可看出，此时并没有原收割机对该机构进行惯性力最小化的设计，而是采取了部分平衡的举措［3］。曲柄上面的配重为零，只在摇杆的位置上加了1．385 kg的配重，下面将对其进行反求设计，探讨一下该机构就其惯性力的平衡是如何进行取舍的。

由于该机构的割刀执行部分是被移动副所包围的，所以割刀及其割刀执行部分是不肯能通过增减配重的方式完全平衡其惯性力的，因此只能进行机构惯性力的最小化计算。通过Matlab计算软件，先确定曲柄和摇杆所加配重的悬臂长度，在运用Matlab的［x，fval］=fmincon优化函数进行多目标函数优化，其整体机构惯性力最小的结果如图3。

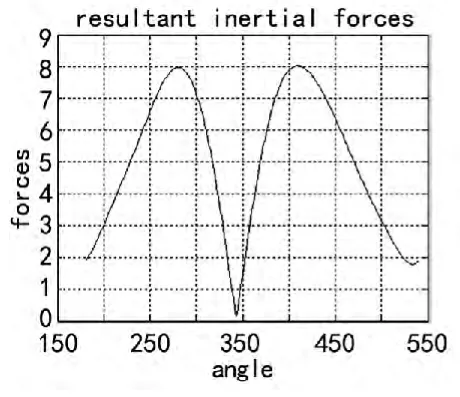
图2 原收割机方案

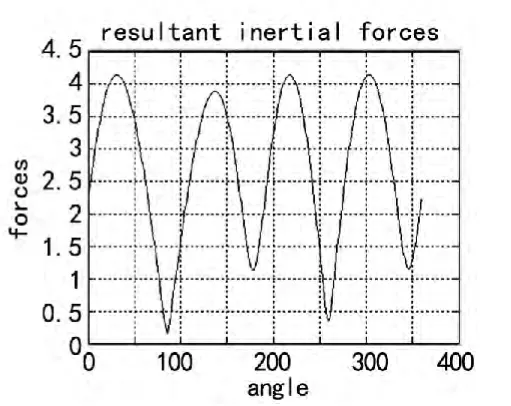
图3 惯性力最小方案

由图3可看到惯性力的峰值为4．1 N，但是在摇杆和曲柄上的配重要加4．07 kg，在计算一组曲柄不加配重，只在摇杆相应的位置上增加配重的情况，此时取摇杆配重的悬臂长度为60 mm。此次计算结果如图5所示。

此计算结果为:摇杆所要施加的配重为2．88 kg，峰值惯性力为6．4 N，配重所在的位置方向为:188．7°。该方案的峰值惯性力较原机器上的减小了1．7 N，也就是减小了20．7%，配重的质量却增加了1．5 kg，也就是52%。而且其在摇杆处配重所需安装的位置会给周围的其他机械部件造成干涉，所以此种方案是不可选择的。当机构在没有进行惯性力平衡的情况下，其惯性力变化情况如图5所示。此时的惯性力的峰值为:16．2 N。为了更好的进行比较建立一个表格［4］，以更形象的方式表现原收割机上所采用的措施更具有优势，其表格如表1所列。

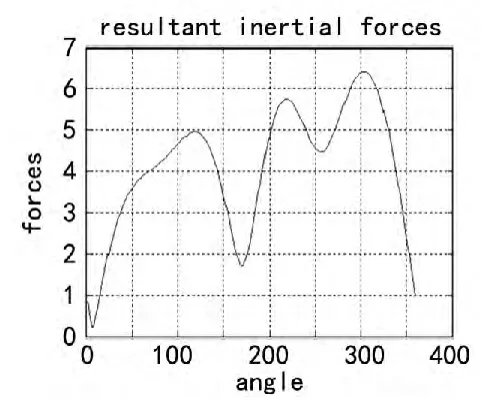
图4 对比方案

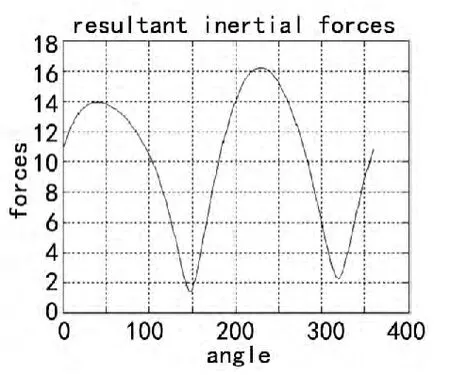
图5 没有进行惯性力平衡方案

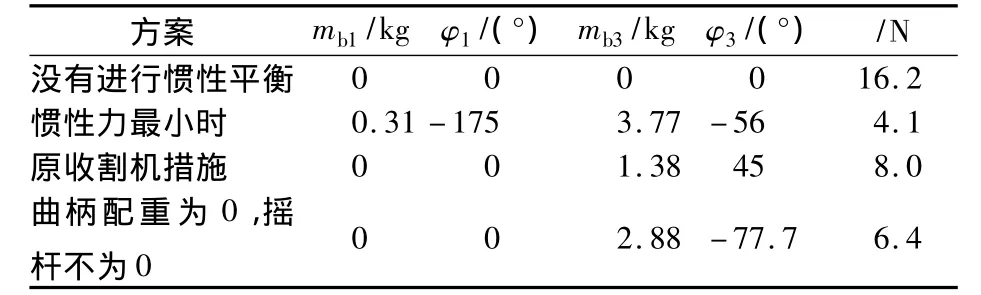
表1 各方案对比表

由表1可看出，在配重悬臂长度都统一的条件下，机构要达到惯性力最小时，要加上4．07 kg的配重质量，但峰值惯性力为4．1 N。而原收割机的机构惯性力峰值为8．0 N，但是只在摇杆的位置上增加了1．38 kg的质量。虽然较惯性力最小的方案上总的惯性力增加了48．75%，但是所需增加的配重却减小了66．9%，而且受割台空间位置的影响在曲柄上添加配重极有可能会对周围的机械构件产生干涉。所以，采取部分平衡只在摇杆的位置上添加1．38 kg，是实际情况中最优的选择［5］。

2 结论

(1)经过以上的论述，可看到割刀执行机构及其传动机构的总惯性力较没有平衡前减小了50．6%，但只是在摇杆的位置上增加了1．38 kg的配重。此种方案消除了一半多的惯性力，然而所付出的代价却是很小的，所以这对于对重量敏感的收割机来说无疑是增加了收割机的机械可靠性、收割效率和使用寿命。

(2)机构惯性力的平衡并不是把所有的惯性力平衡掉就是最优的，在实际生产过程中很多时候要综合多方面的情况来对机械结构进行设计和优化。笔者所论述的实例就很好的解释了这方面的要求，在最终的方案里曲柄上没有增加配重也是降低了生产成本和加工工艺的复杂性，为机器在整个激烈的竞争市场中提供了优势。

［1］ 孙 桓．机械原理［M］．第七版．西安:西北工业大学机械原理及机械零件教研室，2006．

［2］ 张 策．机械动力学［M］．北京:高等教育出版社，2000．

［3］ 王玉新．弹性连杆机构的组合共振［J］．天津大学学报，1996．

［4］ 黄 进．平面机构惯性力和惯性力矩的综合平衡［J］．湖北工学院学报，2002．

［5］ 李兆军，蔡敢为，黄其柏．电动机-弹性连杆机构系统谐振机理研究［J］．振动工程学报，2006．