材料特性参数对金属薄壁元件耐撞性的影响*

陈淑琴，周利强

(1．兰州交通大学机电工程学院，甘肃兰州 730070;2．青藏铁路公司，青海西宁 810000)

0 引言

吸能结构作为轨道车辆被动安全防护系统的重要组成部分，其耐撞性关系到司乘人员的安全及车体结构的完整，从而成为轨道车辆被动安全领域中重要的研究课题。吸能结构通常由各种薄壁元件组成，因此，其耐撞性主要取决于这些薄壁元件的性能。金属薄壁元件因其结构简单、强重比高、成本低，受到碰撞载荷作用时，破坏模式稳定，能以可控的方式通过自身不可逆的塑性变形吸收车辆的碰撞动能，从而成为最传统、最有效的吸能元件广泛用于汽车、铁路列车、船舶和飞机等几乎所有交通工具的碰撞能量耗散系统中［1-3］。因此，笔者主要对金属薄壁元件的耐撞性进行研究。

1 吸能元件常用的耐撞性评价指标

吸能元件的耐撞性通常用以下参数来评价［1］:

(1)总能量Ez:吸能元件在碰撞载荷作用下所吸收的总能量为:

式中:δ为吸能元件的压溃行程;F(s)为碰撞力。

(2)比吸能Es:吸能元件吸收的能量与其质量之比，该值越大，吸能元件的吸能能力越强，公式表示为:

式中:Ms为吸能元件的质量。

(3)初始碰撞力峰值Fcr:吸能元件接触碰撞的瞬间，碰撞力波动较大而变形很小，该区域不利于吸收碰撞能量，减小碰撞减速度，因此，对于耐撞性研究，初始碰撞力峰值应尽可能小。

2 吸能元件在轴向载荷作用下的变形模式

金属薄壁元件在碰撞载荷作用下也会通过横向塑性变形来吸收能量，但横向变形的吸能量大约比轴向差一个数量级［4］。因此，下文主要对金属薄壁元件的轴向变形模式进行介绍，轴向载荷作用下，金属薄壁元件的变形模式主要有以下3种［2］。

(1)渐进屈曲变形，薄壁元件被轴向压缩时，从受压缩的一端开始，逐渐发生屈曲变形，形成多个塑性铰，这种变形模式是吸能元件的最佳变形模式。

(2)整体Euler屈曲变形，这种变形的第一个塑性铰通常发生在吸能元件中部，之后产生较大的横向位移，这种变形模式的吸能效率极低。

(3)混合变形，元件被压缩的初始阶段发生渐进屈曲变形，随后转变为整体Euler屈曲变形，吸能量介于渐进屈曲变形和整体Euler屈曲变形之间。

上述几种变形模式主要取决于薄壁元件的直径与壁厚之比(D/t)和长度L。研究表明，要使薄壁元件发生渐进屈曲变形，应将径壁比(D/t)控制在30左右，且 L/D 应该小于 5［5］。

3 吸能元件碰撞仿真分析

为了研究材料特性参数对金属薄壁元件耐撞性的影响，利用ANSYS/LS-DYNA软件对弹性模量E、泊松比μ、屈服应力σ0和剪切向模Etan不同的薄壁圆管进行碰撞仿真，其碰撞模型如图1所示，圆管长L=400 mm，根据薄壁元件发生渐进屈曲变形的条件，取圆管直径D=80 mm，壁厚t=2 mm，刚性板以v=15 km/h(4．17m/s)的速度碰撞一端完全固定的薄壁圆管，圆管及刚性板的材料参数如表1所列。

图1 薄壁管碰撞模型

表1 材料参数

3．1 弹性模量与耐撞性

当薄壁圆管的弹性模量E=50～200 GPa，增幅间隔为50 GPa，屈服应力 σ0=110．3 MPa，泊松比 μ=0．3，切向模量Etan=450 MPa时，通过数值仿真得到其碰撞力-位移曲线和能量-位移曲线分别如图2和图3所示。从图2中看出，在其他参数相同的条件下，初始碰撞力峰值基本是随弹性模量的增大而增大。从图3中看出，薄壁圆管的压溃行程相同时，弹性模量越大的圆管吸收的能量相对越多。

图2 碰撞力-位移曲线

图3 能量-位移曲线

3．2 泊松比与耐撞性

当薄壁圆管的泊松比μ=0．25～0．35，增幅间隔为0．05，弹性模量 E=70 GPa，屈服应力 σ0=110．3 MPa，切向模量Etan=450 MPa时，通过数值仿真得到其碰撞力-位移曲线和能量-位移曲线分别如图4和图5所示。从图中看出，在其他参数相同的条件下，泊松比对薄壁圆管的耐撞性影响不大。

图4 碰撞力-位移曲线

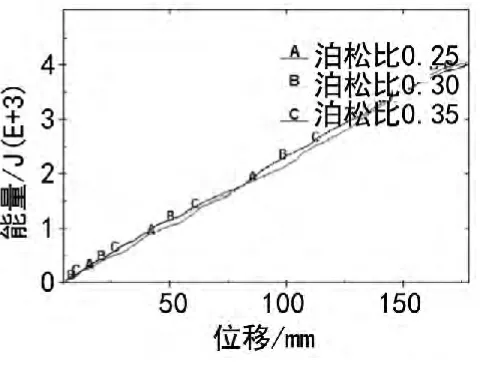
图5 能量-位移曲线

3．3 屈服应力与耐撞性

当薄壁圆管的屈服应力σ0=100～250 MPa，增幅间隔为50 MPa，弹性模量E=70 GPa，泊松比μ=0．3，剪切模量Etan=450 MPa时，通过数值仿真得到其碰撞力-位移曲线和能量-位移曲线分别如图6和图7所示，从图6中看出，屈服应力增大时，整个曲线的波动幅度增大，初始碰撞力峰值也增大，对应诱发其发生塑性变形的碰撞力也增大，不利于减小碰撞减速度。从图7中看出，薄壁圆管的压溃行程相同时，其屈服应力越大，吸收的能量越多。

图6 碰撞力-位移曲线

图7 能量-位移曲线

3．4 剪切模量与耐撞性

当薄壁圆管的剪切模量Etan=300～600 MPa，增幅间隔为100 MPa，弹性模量E=70 GPa，屈服应力σ0=110．3 MPa，泊松比 μ =0．3 时，通过数值仿真得到其碰撞力-位移曲线和能量-位移曲线分别如图8和图9所示。

从图8 中看出，切向模量增大时，整个曲线的波动幅度增大，初始碰撞力峰值也增大。从图9 中看出，薄壁圆管的压溃行程相同时，剪切模量越大，吸收的能量越多。

4 结语

通过对同种材料、不同材料特性参数的金属薄壁元件进行碰撞仿真分析，得出结论: 弹性模量、屈服应力及剪切模量对金属薄壁元件的耐撞性影响较大，而泊松比对其影响较小，这为选择性能良好的吸能结构奠定了基础，对保护司乘人员和车体结构在碰撞事故中的安全有着重要的作用。

［1］ 柳艳杰． 汽车低速碰撞吸能部件的抗撞性能研究［D］． 大连: 哈尔滨工程大学，2012．

［2］ 张宗华． 轻质吸能材料和结构的耐撞性分析与设计优化［D］． 大连: 大连理工大学，2010．

［3］ 谢素超． 铁道车辆结构耐撞性影响因素及优化研究［D］． 长沙:中南大学，2012．

［4］ 陈秉智，伞军民，孙彦彬，等． 薄壁构件的抗碰撞吸能［J］，大连交通大学学报，2008，29( 5) : 99 - 104．

［5］ 杜星文，宋宏伟． 圆柱壳冲击动力学及耐撞性设计［M］． 北京: 科学出版社，2004．