基于自由振动的钢弹簧浮置板阻尼比测试分析

王 金，李玉路，邵文杰，练松良

（1.同济大学道路与交通工程教育部重点实验室，上海201804； 2.安境迩（上海）科技有限公司，上海200030）

目前，振动噪声已经成为城市轨道交通的主要污染源之一。在诸多减振措施中，浮置板轨道结构的效果最好[1]。钢弹簧隔振器是浮置板减振的主要部件[2]，其刚度和阻尼对浮置板的减振效果有极其重要的影响。与刚度测试相比，阻尼比的测试更为复杂，包括自由振动法[3-4]、滞回曲线法[5-6]、对数衰减率法[7]、功率带宽法[7]及函数拟合法[8]等。其中，自由振动法最为直观，即阻尼的存在使得振动衰减幅值变小，根据衰减曲线即可确定其阻尼比。

本文通过锤击法自由振动试验，基于对数衰减率法确定钢弹簧浮置板的阻尼比。

1 测试原理

在弹簧正上方放置一个混凝土质量块（图1），形成等效的单自由度的质量—弹簧—阻尼系统（图2），其自由振动方程为：

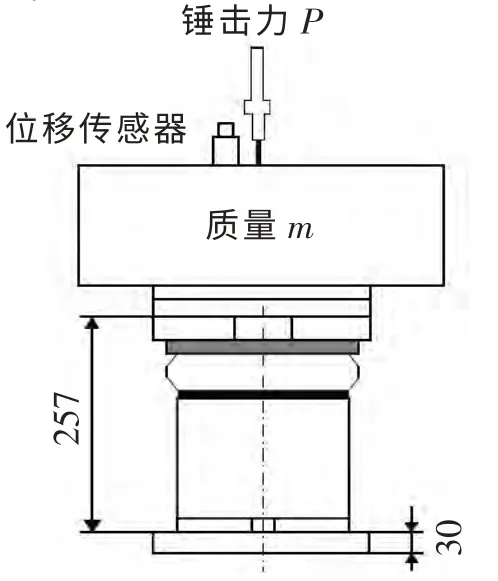
图1 隔振器上放置质量块示意图（单位：mm）Fig.1 Sketch of the concrete block placed on the vibration isolator（mm）

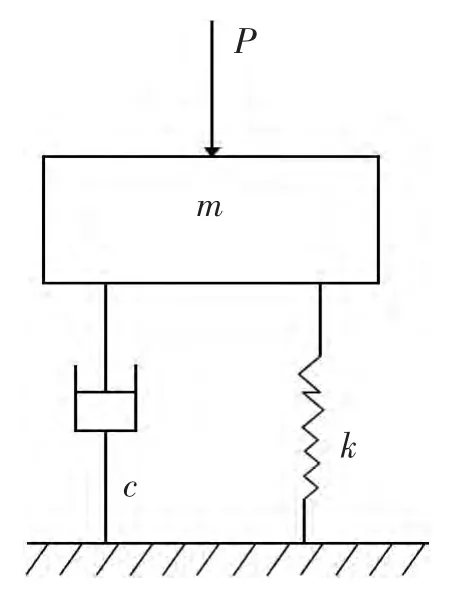
图2 等效单自由度质量-弹簧-阻尼系统Fig.2 Equivalent mass-spring-damper system of single degree of freedom

令u(t)=est，代入式(1)，同时考虑到钢弹簧隔振器为小阻尼体系，得

则

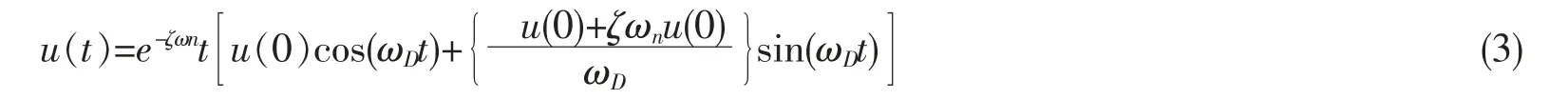
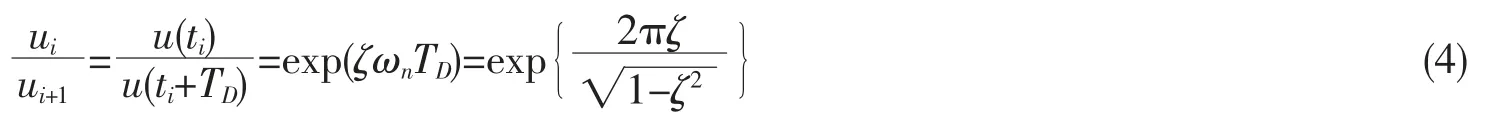
即钢弹簧浮置板相邻振动峰值比仅与其阻尼比有关，与i 的取值无关。称相邻振动峰值比的自然对数值为对数衰减率，用δ 表示

则阻尼比ζ 为

钢弹簧浮置板的阻尼比较小，为了获得更高的精度，可采用相隔几个周期的振动峰值比来计算其阻尼比[7]，如相隔n 个周期，则其对数衰减率和阻尼比为

式中：δ 为单个波形对数衰减率，n 为自由振动波形个数，ui为第i 个波峰幅值，ui+n为第i+n 个波峰幅值。

2 试验测试

在钢弹簧隔振器正上方放置一个混凝土质量块（质量1.7 t，相当于线路上分布在单个钢弹簧隔振器上方的轨道质量，见图3），在质量块上表面中心处放置一块铁垫板，即测力锤（YDL-5H 压电式压力传感器）的锤击位置，那么位移传感器（891-II 型拾振器）就不能放在正中心位置，为了保证测试精度，在靠近质量块中心位置处放置4 个位移传感器（见图4），数据处理时将4 个传感器的位移信号取平均，从而消除质量块两个水平方向的侧摆信号，得到其垂向位移信号。

对测试装置激振时，由同一人对质量块施加大、中、小3 种锤击力，并测量冲击锤的激振力，分析不同激振力对阻尼比的影响。为了消除随机误差，分别对6 个钢弹簧浮置板进行阻尼比测试。

图3 隔振器上放置质量块现场测试图Fig.3 Field test of the concrete block placed on the vibration isolator

图4 位移传感器布置图Fig.4 Layout of the displacement sensors

3 测试结果及分析

3.1 波形分析

某次锤击试验中，实测的冲击锤激振力如图5所示，图6为此次冲击及冲击作用结束后钢弹簧隔振器的垂向位移随时间的变化。

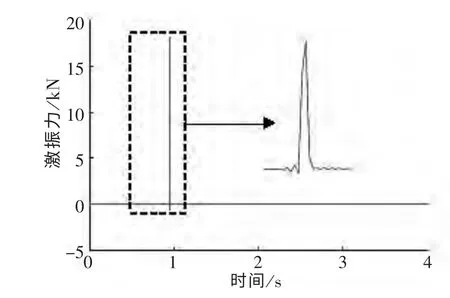
图5 锤击试验实测冲击锤激振力Fig.5 Exciting force of the impact hammer in hammering testing

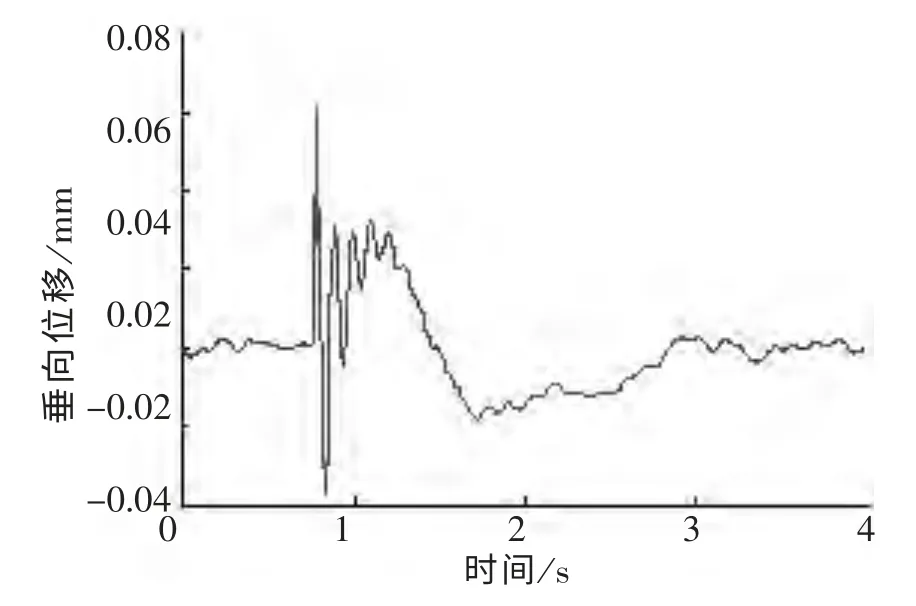
图6 锤击试验钢弹簧垂向位移(滤波前)Fig.6 Vertical displacement of the steel spring in hammering testing (before filtering)

由刚度测试结果（刚度测试不是本文的重点，详细测试及分析过程未列出）可知，钢弹簧隔振器的平均垂向刚度约为4.82～7.16 kN·mm-1。已知钢弹簧隔振器的上置质量为1.7 t，由公式(8)可粗略估计该单自由度系统的固有频率为8.47～10.33 Hz。

式中：f 为固有频率，Hz；k 为垂向刚度，N·m-1；m 为质量，kg。

测试时，质量块的各种模态振动、环境振动等产生干扰信号，为了提高分析效果，必须消除这些干扰信号对测试数据的影响。考虑到系统的固有频率范围为8.47～10.33 Hz，采用通带为7.6～11.4 Hz 的带通滤波器（将固有频率上下限分别放大10%），将自振频率以外的信号滤波。滤波前后的位移信号如图7所示。

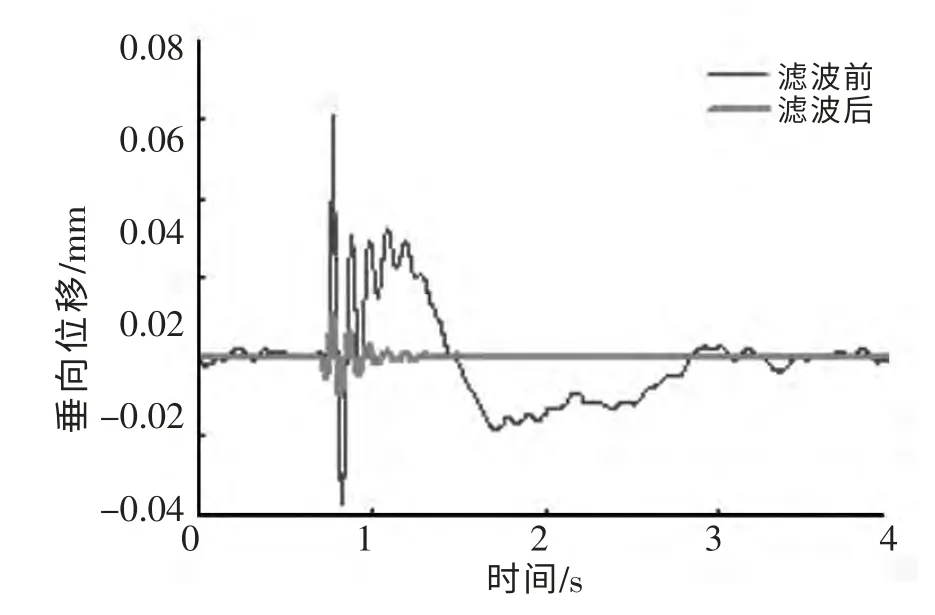
图7 锤击试验钢弹簧垂向位移(滤波前后)Fig.7 Vertical displacement of the steel spring in hammering test (before and after filtering)

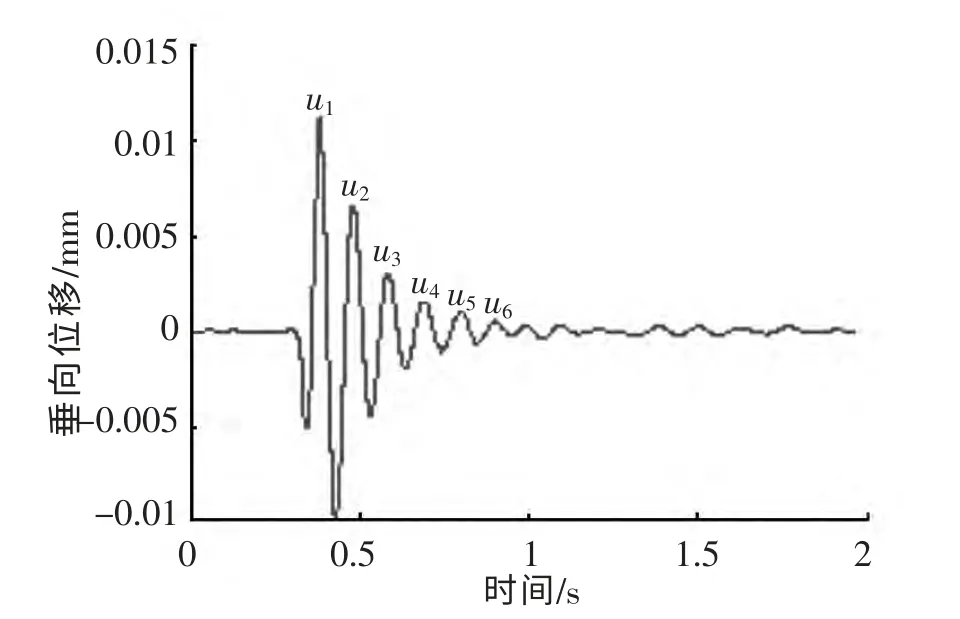
图8 锤击试验钢弹簧垂向位移(滤波后)Fig.8 Vertical displacement of the steel spring in hammering test (after filtering)

3.2 波形间隔个数对阻尼比计算的影响分析

第1 节中指出采用相隔n 个周期的振动峰值可使钢弹簧浮置板阻尼比的计算更为准确，但n 的取值还有待商榷。针对测试滤波后的位移信号（图8）进行分析，并根据式(7)计算其阻尼比，如表1所示。

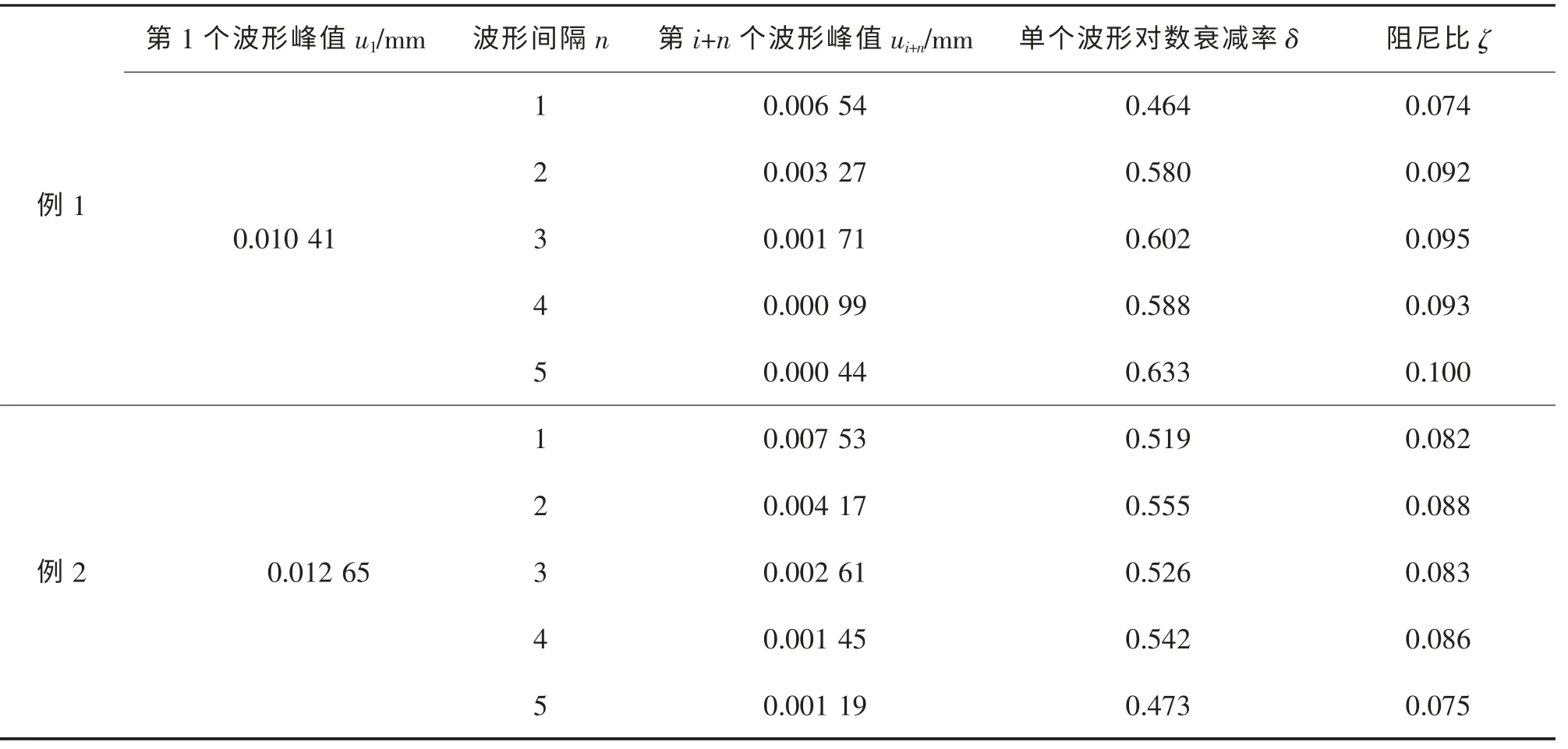
表1 采用不同间隔自由振动波形峰值计算的阻尼比Tab.1 The damping ratio of free vibration waveform peaks at different intervals

由表1可知n 的取值对阻尼比结果有较大的影响，n=1 时的阻尼比偏小，此时的位移峰值大于第1 个波形峰值(u1)的50%；n=2，3 或4 时的阻尼比较为接近；n=5 时的阻尼比或偏大或偏小，此时的位移峰值均小于第1 个波形峰值的10%。考虑到第i+n 个位移峰值(ui+n)占第1 个波形峰值(u1)的比例及阻尼比的计算结果，建议取n=2～4，具体取值应根据实际测试情况判断。此次测试中，n=4 时的阻尼比大于n=2 时的阻尼比，同时小于n=3 时的阻尼比，故这里取n=4，即用第1 个(u1)和第5 个(u5)波形峰值进行计算。

3.3 锤击力大小对阻尼比的影响分析

根据锤击试验时实测的锤击力，将激振力分为小、中、大3 个等级，分别为10～15、15～25、25～30 kN，其阻尼比如表2所示。可知，钢弹簧浮置板阻尼比并没有随着激振力等级的提升而有较大的变化，25～30 kN 激振力锤击作用下6 个钢弹簧的平均阻尼比与10～15 kN 时的平均阻尼比相比的增加在5%以内，在工程所允许的范围之内，故试验时可不区分激振力的大小，或可根据实际应用中需承受的外力的大小来施加激振力，以得到更为准确的结果。

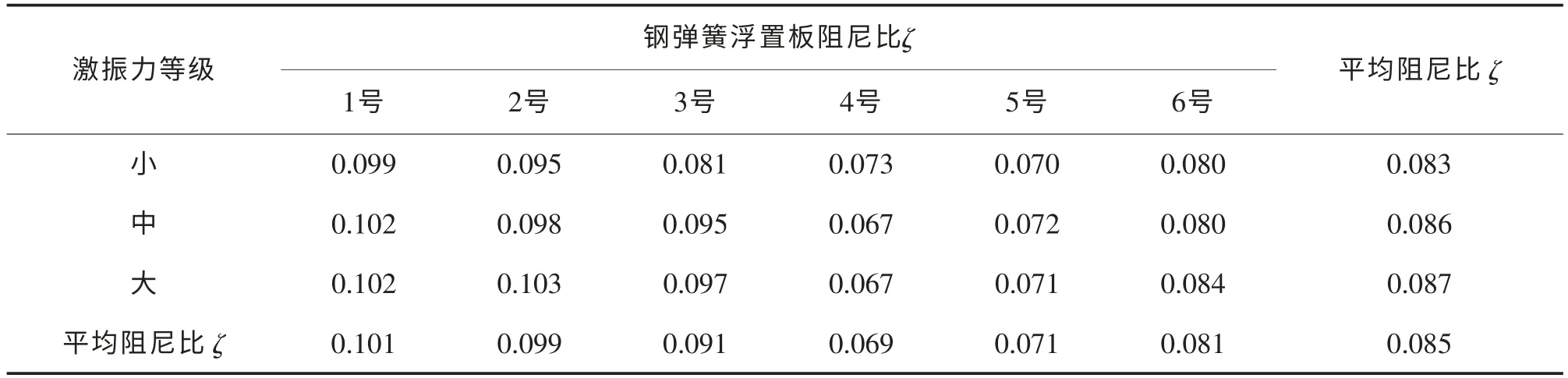
表2 不同激振力等级时钢弹簧浮置板阻尼比Tab.2 The damping ratio of the steel spring floating slab at different levels of exciting forces

4 结论

1） 可通过室内锤击试验得到的自由振动波形衰减曲线计算钢弹簧浮置板的阻尼比，为工程应用研究提供了一种便捷的测试、计算方法。

2） 采用自由振动法计算阻尼比时，自由振动波形的间隔对阻尼比计算结果有较大影响，建议取2～4 个波形间隔，具体取值应根据测试波形确定。

3） 锤击试验中，激振力等级对阻尼比计算结果影响较小，可不区分激振力的大小；但考虑到阻尼的非线性特性，最好能根据其在实际应用中可能承受的外荷载的大小来进行锤击试验。

[1]蒋崇达，雷晓燕.地铁运营下钢弹簧浮置板轨道减振分析[J].华东交通大学学报，2012，29（5）: 23-28.

[2]刘建利.钢弹簧浮置板的现有不足分析及优化建议[J].都市快轨交通，2014，27（6）: 97-100.

[3]柳志远，刘鹏郎，易理.橡胶式扭振减振器固有频率与阻尼比的测试方法比较[J].北京农业工程大学学报，1995，15（4）:13-17.

[4]邓宏道，张祥康，田永乾.用自由振动法测试高阶振型阻尼比的探讨[J].四川大学学报：工程科学版，1983，17（3）:117-120.

[5]刘建峰，徐进，李青松.循环荷载下岩石阻尼参数测试的实验研究[J].岩石力学与工程学报，2010，29（5）:1036-1041.

[6]王杰，赵寿根，吴大方，等.微振动隔振器动态阻尼系数的测试方法[J].航空学报，2014，35（2）:454-460.

[7]刘晶波.结构动力学[M].北京：机械工业出版社，2007：46-48.

[8]周建鹏，陈昌锡，曹永上.在用汽车减振器阻尼测试方法[J].上海工程技术大学学报，2004，18（1）: 3-5.