带水线的斜拉索气动特性数值分析

黄贻凤

（华东交通大学轨道交通学院，江西 南昌330013）

随着斜拉桥结构跨度或高度的不断增加，结构变得越来越柔，对风的敏感性也随之增加，风荷载成为控制结构设计的关键因素之一。拉索是斜拉桥的关键构件，考虑到拉索的柔性、相对小的质量及较低的阻尼，在风或支承端的作用下易产生强烈的横向振动。拉索的振动不仅会给行人带来不舒适感和不安全感，同时它也会使拉索产生疲劳，破坏拉索的防腐系统，严重地影响拉索的寿命[1]。拉索的风雨激振是在风和雨的共同作用下发生的大幅低频的振动，是振幅最大、危害最严重的一种风致振动。风雨激振时，拉索的上下表面各形成一条雨水水线，沿拉索往下流。在拉索振动时，水线在拉索表面振荡。1998年的国际桥梁空气动力学学术会议上，拉索风雨激振被确定为未来一段时间的四大重点问题之一[2]。大量观测和实验表明风雨激振给桥梁带来巨大的破坏性，严重危害桥梁的安全，对风雨激振形成的机理和控制措施的研究刻不容缓。

为了确定水线对拉索气动特性的影响，本文采用计算流体动力学软件FLUENT 分别对设置不同大小水线的拉索进行数值风洞试验，对带水线的拉索绕流进行模拟，研究水线对拉索绕流的影响，计算各种工况拉索的三分力系数，并与同条件下的光面拉索进行对比研究。

1 计算模型的选取

已有文献表明[3-4]：拉索倾角α=30°左右，风向角β=30°～35°最易发生风雨激振，且水线位置角为40°左右时拉索的振动幅度较大。故本文选择拉索倾角α=30°，风向角β=35°，水线角θ=47°。各角度的含义见图1所示。其中，以拉索中点为原点画坐标轴，将迎风一侧的水线定义为上水线，背风一侧的水线定义为下水线；Fd，Fl分别为气流流经所受到的阻力和升力。已有研究表明[5-7]：上水线是风雨激振产生的主要原因，下水线对拉索风雨激振影响非常小。本文仅考虑上水线的存在对于拉索周围流场的影响，本文所提到的水线就是指上水线。水线角θ 为上水线断面和原点连线与纵轴正向所成角度，用它来控制上水线位置[8]。

图1 各角度含义的示意图Fig.1 Diagrammatic sketch of various angles

在风洞试验中，人们常采用的人工水线形状有：圆弧形、圆形、矩形、八字形等[9]。已有风洞试验中观察到：上水线的外形最接近圆弧形[6]。因此，为验证不同大小水线对拉索气动特性的影响，本文采用大小不同的3 种水线，截面均为圆弧形。3 种水线的弦长b 均为20 mm，水线高h 分别取为4，8 和10 mm。弦长b 和高h 的含义如图2所示。为了确定水线对拉索的影响，同时还选取了同种尺寸同样放置状态的光圆拉索做对比数值风洞试验。

取拉索直径D=0.2 m，拉索在高度方向的投影长度均为3.6 m，计算域为：长×宽×高=（50D+索在长度方向的投影长度）×（20D+索在宽度方向的投影长度）×18D，入口边界到拉索中心距离为10D，出口边界到拉索中心距离为40D，左右边界到拉索截面中心的距离均为10D，计算域见图3。已有研究表明[10]：雨振只在风速为8～18 m·s-1的范围内发生，故本文选择的风速为15 m·s-1。

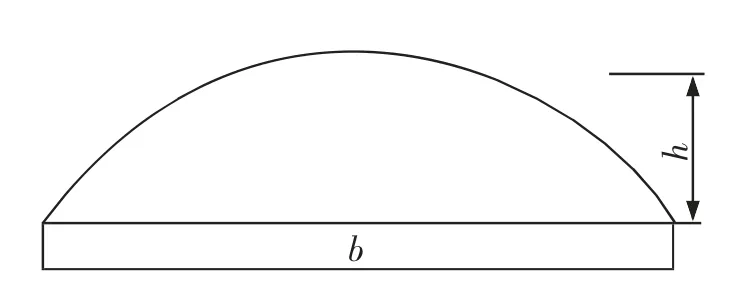
图2 水线大小Fig.2 The size of the waterline

2 网格划分

对带水线的拉索进行结构化网格划分，网格如图4所示。图4仅示出了h=10 mm 水线拉索的网格图。

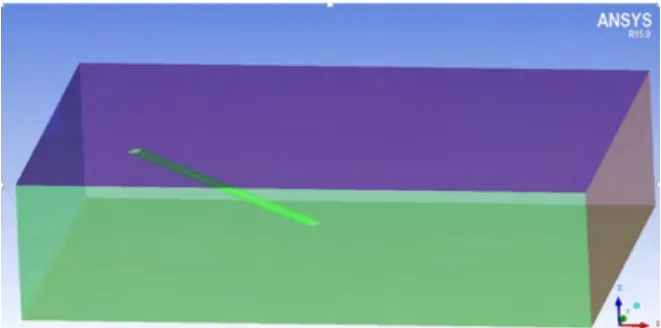
图3 计算域示意图Fig.3 The computing domain

图4 带水线拉索结构化网格划分的局部网格图Fig.4 The fractional grid graph of structuring grid for the stayed cable with waterline

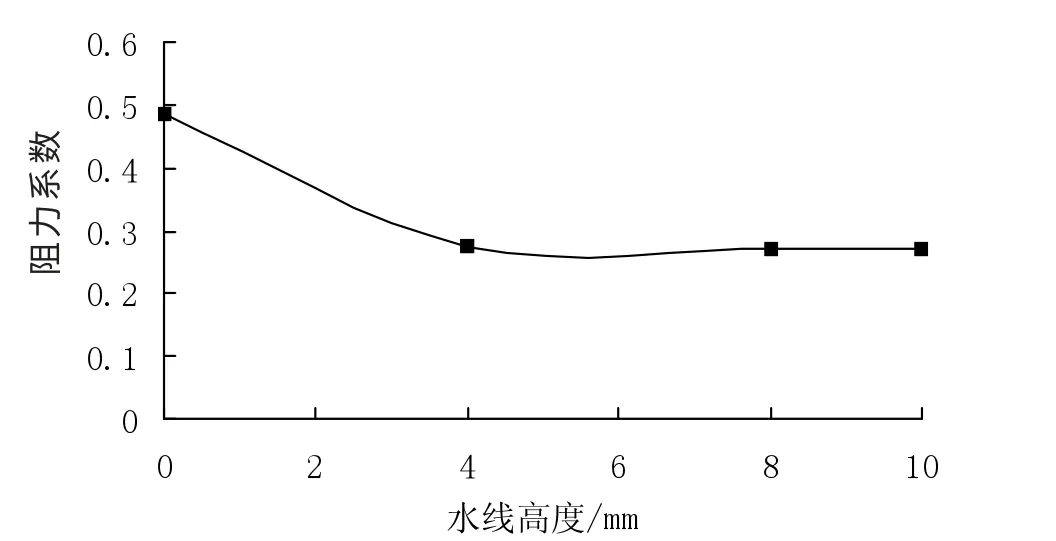
图5 （a） 阻力系数

3 计算结果

计算结果见图5，从图5可以看出。

1） 带不同高度水线的拉索，其三分力系数差别很小，因而水线高度对三分力系数的影响不明显，这可能与它们同处亚临界状态有关。这与A Bosdogianni，D Olivari 的结论是一致的[5]。随着水线高度的增加，阻力系数和升力系数均小幅变小，而升力矩系数则先变小后变大。

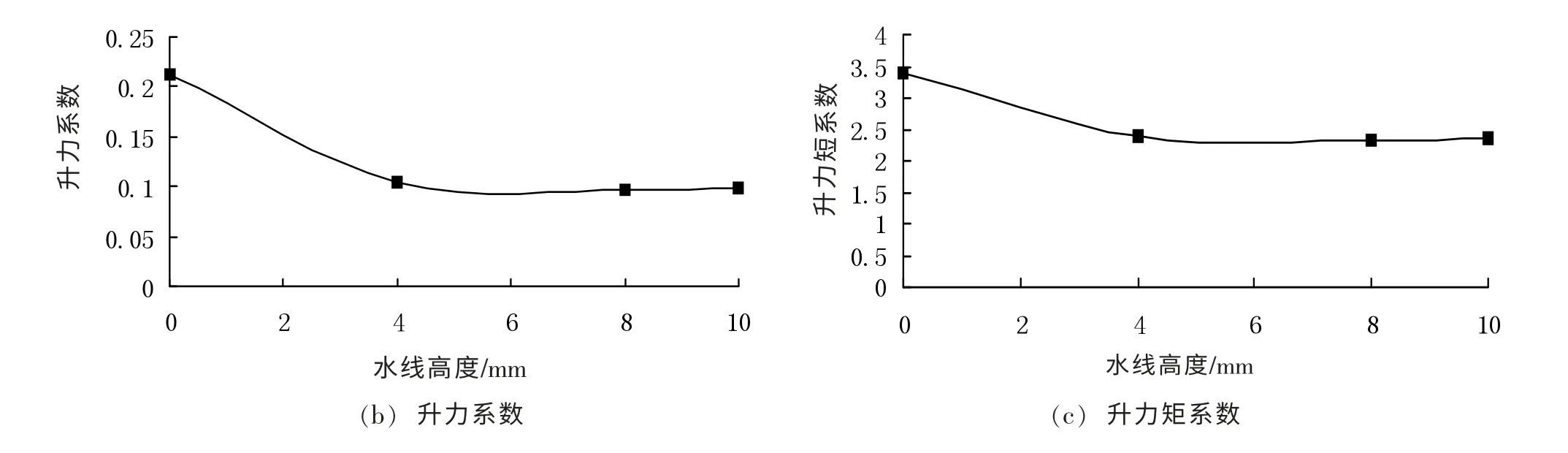
图5 三分力系数随水线高度的的变化趋势图Fig.5 The tendency chart of the three force coefficients along the height of the waterline

2） 虽然水线的截面积与拉索的截面积相比是微乎其微的，但设置了水线后，由于改变了拉索的外形，三分力系数均明显变小。阻力系数减小约0.21，降幅43%左右；升力系数减小约0.11，降幅53%左右；升力矩系数减小约1.04，降幅30%左右。以上结果表明：由于水线的存在，水线附近拉索的表面压力产生急剧变化，进而引起三分力系数的急剧变化。根据准定常假设，处于平均气动升力的负斜率区，则有可能存在驰振不稳定性，导致拉索大幅振动；所以水线的存在可能导致拉索的不稳定。

4 结语

采用FLUENT 软件分别对设置不同大小水线的拉索进行了数值风洞试验，计算各种工况拉索的三分力系数，并与同条件下不设肋条的光面拉索进行对比研究。计算表明：

1） 拉索设置水线后，虽然水线尺寸很小，但水线对三分力系数的影响很大，设置水线后三分力系数均明显变小，水线的存在可能导致拉索的不稳定。

2） 由于带不同高度水线的拉索同处亚临界状态，水线高度对三分力系数的影响不明显。

[1]刘旭政，张春荣，陈水生.基于模糊神经网络的拉索耐久性评价模型[J].华东交通大学学报，2010，27（2）：8-12.

[2]林海霞．斜拉索之悬念[J]．国外桥梁，1999（3）：75-77.

[3]GU MING，DU XIAOQING．Experimental investigation of rain-wind-induced vibration of cables in cable-stayed bridges and its mitigation[J].Journal of Wind Engineering and Industrial Aerodynamics，2005，93（1）：79-95.

[4]杜晓庆.斜拉桥拉索风雨激振研究[D].上海：同济大学，2003.

[5]BOSDOGIANNI A，OLIVARI D.Wind-and rain-induced oscillations of cable of stayed bridge[J].Journal of Wind Engineering and Industrial Aerodynamics，1996，64：171-185.

[6]李寿英.斜拉桥拉索风雨激振机理及其控制理论研究[D].上海：同济大学，2005.

[7]GU MING，DU XIAOQING，LI ShOUYING.Experimental and theoretical simulations on wind-rain-induced vibration of 3-D rigid stay cables [J].Journal of Sound and Vibration，2009，320：184-200.

[8]余康烨.斜拉桥拉索振动及其抑振研究[D].武汉：华中科技大学，2007.

[9]许林汕，葛耀君，赵林.高精度风雨模拟环境下拉索风雨激振试验研究新发现[J].土木工程学报，2011，44(5)：86-93.

[10]YAMAGUCHI H.Analytical study on growth mechanism of rain vibration of cable[J].Journal of Wind Engineering and Industrial Aerodynamics，1990，33：73-80.