基于PM方程的指纹扫描仪图像增强算法研究

刘晓薇

（江西科技师范大学数计学院，江西 南昌330013）

目前的指纹扫描设备采用的都是基于光学结构和CMOS（complementary metal oxide semilonductor）图像传感器的采集原理。在高质量指纹采集扫描仪中CMOS图像传感器约占整机总成本的30%～50%，为了减少成本，缩小体积，大多数指纹扫描仪都会选用CFA 模式的CMOS 图像传感器，现在应用最多的是采用GRBG 排列布局的Bayer 格式阵列，因为绿色光谱对应人眼对可见光光谱敏感度的峰值，采用双倍的绿色像素数可以加强感光效果［1］。

即使在CFA（cdor filter array）模式传感器中，因为感光元的大小差异，分辨率不同，价格也有10～20倍的差异，一些CMOS传感器在一些特殊指纹的采集上因清晰度及噪声等达不到要求而造成采集困难，加上图像光路采集传输系统本身的噪声干扰和非线性失真，对于指纹图像，容易引起许多伪特征和丢失很多真实特征，严重影响后续的指纹比对和验证，因此图像去噪和指纹细节增强是指纹图像处理中非常重要的环节。怎样用低端CMOS传感器得到符合FBI（Federal Bureau of Investigation），GA（公安）等标准的图像，是目前指纹扫描仪中图像处理算法要着重解决的问题。

1 基于PM方程的图像增强算法研究

在传统的指纹图像噪声滤波算法，如中值滤波，高斯滤波等［2］，主要将图像的高频成分滤除，由于指纹纹理的图像信号相对背景来说，也分布在高频区域，因此在对噪声进行滤波的同时必定损害到指纹的特征信息。

为了既保留指纹的特征细节信息，又能够提高图像的对比度及分辨率，这里提出了一种改进的基于PM方程和USM的去噪增强算法，比较好的解决了提高图像分辨率（或者MTF（modulation transfer funation））和去除噪声的矛盾，整个算法流程主要包括3个部分，首先采用自适应算法消除图像的马赛克效应，然后采用优化的USM（unsharp mask）锐化算法，同提高图像边缘的清晰度，结合改进的PM噪声滤波算法，几乎在不损害图像指纹细节的前提下，有效地去除了指纹图像存在的高斯噪声和随机噪声。

1.1 去马赛克算法

因为光照和CFA的特性，在采集的图像中存在通道不均匀的现象，也就是马赛克效应，通常去除马赛克的算法采用二次或者三次插值的算法［3-5］，即根据每个点周围的4个或者16点对该点进行插值，这种算法通过对图像平滑在解决通道不均匀方面能够取到一定的效果，但是不可避免的会引起边缘或者纹理的模糊，导致分辨率的下降，在这里中，采用了基于边界的自适应插值算法，即首先分别计算插值点的X方向和Y方向梯度，决定边界的方向，然后沿着边界方向进行插值参数的提取。参照图1所示的布列模板，具体算法流程如下。

1）首先计算水平方向的梯度

图1 CFA制式图像模板Fig.1 The templet of CFA

2）然后计算垂直方向的梯度

3）进行插值

其中：ΔH为水平方向的梯度；ΔV为垂直方向的梯度；R，G，B变量分别表示不同通道中的分量。

1.2 优化的USM图像锐化

为了抑制噪声，在采集原始图像时候，增益不能调的过高。由于指纹扫描设备本身光学系统的畸变，采集的图像分辨率对一些干性指纹，或者残缺的指纹不能满足要求，这里采用了USM 算法对图像进行锐化，USM的锐化模型可以公式表达为

其中：i、j为像素的坐标；f(i,j)为输入图像；y(i,j)为输出图像；而z(i,j)为校正信号；λ是用于控制图像边缘锐化强弱的松弛因子。z(i,j)一般可以通过下式获取

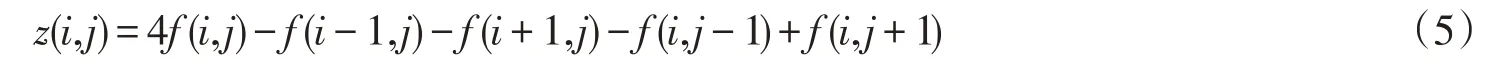
这种算法的主要缺点是对噪音非常敏感，尤其在图像变化比较缓慢的地方的噪音。另外对于图像的边缘（高对比度区域）会出现增强过头的现象。因此这里采用类似于Photoshop的USM算子原理，用二维高斯函数g(i,j)［6］作模糊滤波器，得到虚化后的图像image_g(i,j)。最终根据平滑后的图像和原始图像之间的差值大小决定是否对图像进行锐化，图像锐化如公式（7）所示，设，其中σ为高斯平滑半径，得到

其中：参数Δv=f(i,j)-image_g(i,j)；amount控制锐化的强弱，过弱锐化效果不明显，过强容易引起噪声；Threshold参数用来判断是否对该点进行锐化，偏大将忽略弱边缘的锐化，偏小则容易对一些噪声进行强化。

随着σ半径的增大，图像的对比度逐渐变强，边缘越发明显，但在σ增大的同时，时间也是几何增长。为了保证算法的实时性，这里提出了一个与窗口半径无关的USM锐化算法，即用局部均值代替高斯平滑函数，同时因为局部均值可以用积分图进行计算，在实际应用中可以保证算法的实时性。设

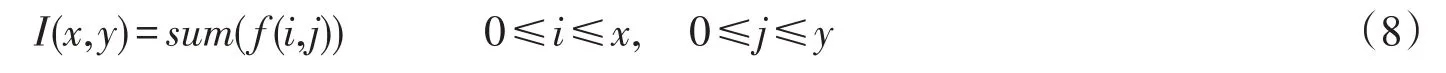
其中：sum为求和运算。

得到局部均值

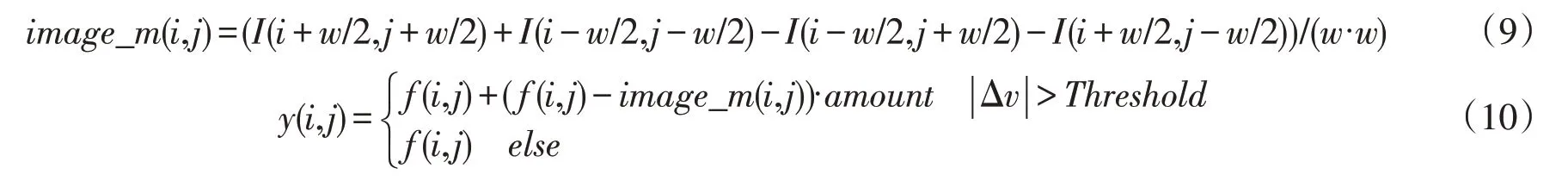
从公式（9）可看出，计算时间与窗口w大小无关，同时在实际应用中，调节后的指纹图像随着σ半径的增大并未出现明显的噪音增强现象，效果比较理想。

1.3 改进的基于PM方程的图像噪声滤波算法

如前所示，传统的噪声滤波算法在滤除噪声的同时，或多或少都可能会损坏图像中的某些高频信息，从而引起模糊边缘和纹理效应，特别是对指纹纹理这种非常敏感的信号。综合考虑多种处理算法，在这里采用了基于PM方程的各向异性扩散偏微分方程滤波算法［7-8］，这个算法由Perona 和Malik提出，根据图像不同方向上的梯度，在非线性尺度空间，确定扩散系数［9］，其方程表达式为

其中：u是图像对应某一个像素点的灰度值；▽u为梯度；div 是散度算子；t表示扩散时间即迭代的步长；c表示扩散系数，其方程如式（12）所示［10-11］，为图像在某点梯度的非负单调递减函数

其中：k表示扩散系数中的一个恒定参数，这个参数控制扩散强度。PM方程的离散化公式可表示成

其中：q表示图像像素的位置；uq为图像像素q处对应的灰度值；▽uq,p=up-utq；λ表示扩散速率的一个常数参数；Nq表示像素q的邻域，通常取图像的左、右、上、下四邻域，如果加上斜对角领域可以得到更好的效果，但影响算法实时性；t为实时迭代次数。以图像在不同方向上的梯度的单调递减函数作为各向异性扩散的扩散系数，使得在同质区域内部，它的扩散系数较大，可以有效滤除该区域内的噪声，而在边缘区域因为灰度值变化剧烈，梯度较大，对应的扩散系数较小，因此能较好地保留指纹图像纹理的边缘信息。

PM方程算法滤除噪声和保留细节的性能较传统算法有了较大的提升，但是随着迭代的增加，边缘被平滑的风险增大，其边缘保持的条件是 ||▽u＞k，在实际应用中，因为不同区域噪声强弱不同，这时对强噪声区域，平滑区域，边缘区域的参数应当自适应调整，同时为了减少迭代的次数，在比较各种PM改进算法的基础上，考虑实时性的要求，这里提出了基于局部归一化方差的自适应扩散系数

其中：σ20即为局部方差。在这里局部方差也采用积分图快速算法来进行计算。具体公式这里不推导，只给出计算过程。设

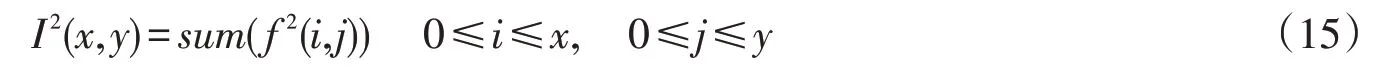
可推导出局部平方灰度值

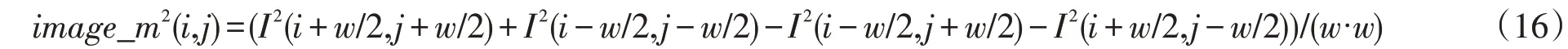
得出局部方差

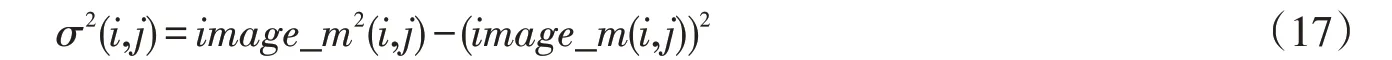
从而得到归一化的局部方差

从式（18）可推出在平滑区域，扩散系数趋于0，在强噪声区域，扩散系数趋于1，满足扩散系数的要求，其边缘自适应定位能力和迭代时间皆优于前面的算法。

2 实验结果分析

为检验本算法在实际应用中的效果，这里采用FBI对指纹图像认证的Mitre公司的MTF检测软件，采用标准检测模板和CTF评价系数来检测本算法的有效性。从图2可以看出，图像经过1.1提出的去马赛克算法处理之后，基本没有存在通道不均衡的现象，图像的标准偏差大幅度降低。

图2 去马赛克算法处理结果Fig.2 The filtering effects of demosaicking

图3 图像经USM和PDE处理结果Fig.3 The processing results of improving USM and PDE

图3（a）图像在经过优化的USM 锐化之后得到图3（b），虽然边缘对比度得到了明显的增强，但是不可避免还是会引起部分噪声，而在经过改进PM滤波之后得到图3（c），在低频区域，噪声几乎可以忽略不计，并且迭代次数较原PM算法缩短了一倍，Mitre的MTF测试软件得出CTF系数结果如表1所示，从结果可以看出，在经过算法处理之后，各个对线频率（Tar Freq）的指标都有了明显的提升。其中，cy/mm为每毫米的采样频率，Peak CTF为对比度函数的极大值。

表1 MITRE’S MTF Software 测试结果Tab.1 The testing results of MITRE’S MTF Software

[1] BLANKSBY A J,LOINAZ M J.Performance analysis of a color CMOS photograph image sensor[J].IEEE Trans Electron Devices,2000,47(1):55-64.

[2] 蒋先刚.基于Hessian特征的视网膜血管图像的增强滤波算法[J].华东交通大学学报,2013,30(3):37-43.

[3] RAJEEV RAMANATH,WESLEY E SNYDER.Adaptive demosaicking[J].IEEE Trans Journal of Electronic Imaging, 2003,12(4):633-642.

[4] KAKARALA R, BAHARAV Z.Adaptive demosaicking with the principal vector method[J].IEEE Trans Consumer Electron,2002,48(4):932-937.

[5] 刘晓松,杨新,文俊.一种用于数字图像传感器的彩色插值算法[J].中国图像图形学报,2003,8A(5):516-523.

[6] PERONA P,MALIK J.Scale space and edge detection using ansotropic diffusion[J].IEEE Trans PAM I, 1990,12(7):629-639.

[7] ANDREA POLESEL, GIOVANNI RAMPONI.Image enhancement via adaptive unsharp masking[J].IEEE Trans Image Processing,2000,9(3):505-510.

[8] ILYA POLLAK, ALAN S WILLSKY.Image segmentation and edge enhancement with stabilized inverse diffusion equation[J].IEEE Transaction on Imae Processing,2000,9(2):256-266.

[9] 宋建军,侯志强.基于人类视觉模型的各向异性扩散滤波方法[J].中国图向图形学报,2012,17(3):321-327.

[10] 陈卿,胡绍湘.基于边缘扩散的医学图像非线性去噪算法[J].计算机应用研究,2011,28(8):3178-3180.

[11] 蒋先刚,许伦伦.基于三维各向异性扩散的图像平滑及三维重构效果分析[J].华东交通大学学报,2010,27(3):78-82.