基于CAA的高速动车组气动噪声仿真研究

王成强，邢海英，郑继峰

（1.长春轨道客车股份有限公司技术中心, 吉林 长春130062; 2.华东交通大学轨道交通学院，江西 南昌330013）

气动噪声功率增长速度是列车运营速度的六次方，因此随着运营速度的不断提高，气动噪声在列车总噪声水平中的贡献会发生显著地变化［1］。运行速度低于250 km·h-1时，机械旋转噪声为列车主要的噪声源；当运行速度高于300 km·h-1时，气动噪声则成为主要的噪声源。因此，考虑高速列车降噪问题必须着重考虑气动噪声的问题［2］。

与流体力学一样，理论分析、实验研究和数值仿真是研究气动噪声问题的3种基本手段。传统气动声学的研究主要以理论分析和实验研究为主，但随着数值计算理论的飞速发展和高性能计算机的出现，采用数值技术来模拟气动声学问题变得可行。计算气动声学自20世纪80年代中期开始逐步兴起，在90年代成为研究热点，如今已经成为科学研究和工程应用的重要研究手段［3］。孙振旭等［2］通过仿真，研究了车体不同部位对气动噪声贡献，分析了高速列车远场气动噪声特性。张军等［4］基于大涡模拟和气动声学理论，对高速列车气动噪声进行仿真，分析气动噪声的分布特性。郑拯宇等［5］将边界元与流体动力学有机结合，实现了基于表面偶极子声源的列车气动噪声外辐射场的数值仿真，研究了列车气动噪声外辐射场特性。

目前国内的研究都集中在对动车组气动噪声场的整体特性方面，对受电弓等细节关注不够。文章在研究计算气动声学（computational aeroacoustics，CAA）基本理论的基础上，建立了CRH3A动车组的CAA模型，分析了受电弓周围气动噪声特性，为列车外形设计与降噪提供参考。

1 CAA理论基础

1.1 控制方程

气动噪声计算的控制方程有多种，其中应用最广的是FW-H（Ffowcs Williams-Hawkings）方程［6］。为了推导FW-H 方程，引入Heaviside 函数H(f)及其导数函数δ(f)

H(f)函数乘以连续方程和动量方程中的所有流动参数，便可以推导出FW-H方程，其表达式[7]为

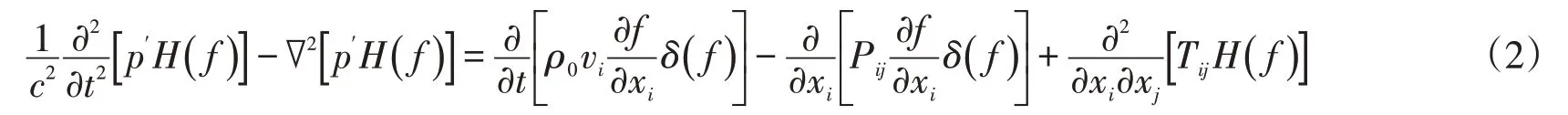
其中：c为声速；ρ′为空气密度波动量；ρ0为未受扰动的空气密度；vi为曲面上某生源点x的法向速度；Pij为应力张量；xi、xj为观测点x处的坐标；Tij=Pij+ρuiuj-c2ρδij；ui、uj为速度分量；δij为克罗内克符号。

1.2 求解方法

高速动车组气动噪声问题涉及空气动力学和声学两大学科，相应的气动噪声问题可分为噪声在列车流场中产生及在声场中传播两阶段。气动噪声计算时，上述两阶段可同时计算，也可分开计算。综合国内外的研究，气动噪声计算方法有纯理论法、半经验法、纯数值法以及CFD 同“声类比”相结合的方法（又称混合法）［8］。混合法克服了半经验法和纯理论法对列车外形及运行状态的限制，使求解结果更加接近物理实际；同时，与纯数值方法相比，显著提高了远场噪声计算效率［7］。

采用混合方法来计算CRH3A动车组气动噪声，计算过程如下。

首先，用RANS（雷诺平均模拟）方法进行动车组定常流仿真。该过程采用CFD++商业软件包，湍流模型采用二方程cubick-ε模型［9］，应用各项异性的湍流模型计算初始流场，产生噪声计算的初始流场和初始噪声信号输入。

其次，以CFD++结果为输入，应用非线性声学（non-linear acoustics solver）NLAS 方法［10］计算近场噪声。

最后，采用FW-H 声学比拟法计算远场观测点噪声。

2 气动噪声仿真分析

利用上述理论与方法，建立CRH3A动车组的CAA模型，并进行仿真计算。

2.1 仿真模型

动车组外形复杂，且编组运行，在现有技术条件下，采用完全真实模型进行气动噪声仿真几乎是不可能的。实际分析过程中，对列车模型进行了适当简化，如将波纹状风挡简化为平板状，忽略空调导流罩进气与散热孔等。简化后的列车采用3节车模拟，即整个模型由1节头车、1节尾车和1节中间车组成，如图1所示。

图1 几何模型Fig.1 Geometric model

计算区域尺寸，在试算的基础上，以3辆编组列车的长度L为特征长度，来流方向为1L，出口方向为2L，高度为0.53L，宽度为0.8L，车体底部离地面的距离为实际距离0.002 35L，如图2所示。

图2 计算区域Fig.2 Schematic diagram of the computational domains

采用分块划分的原则对模型进行网格划分，以降低对内存的需求，提高效率。网格划分过程中，对受电弓等车体附件区域采用较小的网格，对远离列车表面的区域采用较大的网格；尾流区网格进行细化，以充分反映该区域的复杂的涡流情况。受电弓区域及车头局部网格划分如图3所示。

图3 局部网格模型Fig.3 Local mesh

2.2 边界条件与湍流模型

根据动车组实际运行环境，CFD仿真计算边界条件设置如下：①列车表面为固定壁面，无滑移和穿透；②地面为移动壁面，速度为负列车速度，无滑移和穿透；③入口、出口以及远场由特征线方法给出，速度为负列车速度。

在NLAS计算声场时，入口、出口及远场边界条件应设置为吸收层边界。

列车周围空气为理想气体，为了得到比较详细的流场统计信息，在流场求解时采用了非线性的湍流模式，即cubick-ε模型。

2.3 仿真结果与分析

文章以250 km·h-1为例，对CRH3A动车组流场和气动噪声特性进行分析，并分析运行速度对列车近场噪声的影响。

2.3.1 流场

利用上述模型，采用CFD++商业软件对动车组流场进行仿真求解。图4为列车湍流动能分布云图，图5为受电弓区域流场云图。

从图4可以看出，在受电弓的上游区域，从第一导流罩到第五导流罩，其周围的湍动能强度均较低；而在受电弓下游区域的3个导流罩，则均为略微高强度的湍动能所覆盖，说明该区域可能成为重要的气动噪声源。

图5表明，受电弓的滑板、下拉杆以及几个绝缘子等位置均存在较大的湍动能，其中风挡下游的壁面拐角位置由于受到了风挡内三维旋转涡系的影响更为突出，成为重要的气动噪声源。

图4 列车湍动能云图(单位：E/(m2·s-2))Fig.4 Turbulent intensity contour of the train

图5 湍动能云图（单位：E/(m2·s-2)）Fig.5 Turbulent intensity contour

2.3.2 气动噪声

2.3.2.1 近场噪声

在RANS 计算结果基础上，采用NLAS 方法将这些统计意义上的流场变量进行湍流脉动信号重构，进行高速列车气动噪声的非定常计算。近场测点气动噪声在NLAS 计算完毕后可以直接通过对脉动压力做FFT获得声压频谱曲线。

受电弓区域是高速列车顶端一个比较重要的扰流区域，布置5个测点，如图6所示。测点1位于受电弓下游滑板中间位置，测点2位于受电弓上游滑板中间位置，而测点3位于中部滑板的端点位置，测点4位于下臂杆上端点水平下下游平移0.5 m 所在的位置，测点5为由空气弹簧中心点向后平移0.5 m所在的位置。测点1～4的声压频谱曲线如7图所示。对测点的最大声压级进行统计分析，可以得到各点的最大A计权声压级，如表1所示。

图6 测点布置示意图Fig.6 Schematic diagram of probes configuration

图7 测点声压频谱曲线Fig.7 Frequency spectrum of the probes

表1 测点最大A 计权总声压级Tab.1 Comparison of SPL for different probes

受电弓区域所有测点最大噪声声压级出现在受电弓滑板中间位置，约123.2 dBA左右；其它测点噪声均集中在101～122 dBA之间，属于比较强的噪声声源。由于本文所用测点均在受电弓或绝缘子柱体的下游，表1中各测点值比从湍动能分布云图中得到的预测值要低。

2.3.2.2 远场噪声

通过NLAS 计算可以得到近场噪声分布特性，然而，要进行远场噪声特性分析，需要通过FW-H 声音传播方程进行求解。首先在列车车体周围建立噪声积分面，然后通过NLAS的非定常计算在该积分面上进行数据积累，进而通过FW-H 方程求解远方测点噪声。

为了考察列车远场噪声沿着X方向的分布，根据ISO-2005-3095的要求选择远场噪声观测点：选取距列车铁轨中心横向25 m，高3.5 m的线上，取X从-60 m到60 m间隔为10 m的点，共13个点。对于这13个测点，以来流方向为正，将列车正中位置测点编号为0，向下游方向每隔10 m命名一个测点，分别为1到6；向上游方向每隔10 m命名一个测点，分别为7到12，如表2所示。

通过对各点声压频谱曲线进行统计分析，可以得到各点的最大A 计权声压级，如表2所示。对车身区域段远场测点做积分求解，可得：Leq=86.96 dBA。

表2 远场噪声测点A计权总声压级Tab.2 Comparison of SPL for far field noise

在X方向上，各测点的声压级分布如表2所示。表2表明，远场噪声在轴向分布上，其极大值出现在列车中部偏上游位置，从头车鼻锥开始到中间车车身，列车均处于高噪声状态。越向下游发展，噪声水平逐渐降低。另外，越往上游发展，远离头车流线型，远场噪声的幅值也会逐渐降低。

2.3.3 运行速度的影响

为了分析速度对列车气动噪声的影响，文章对了160，200，220，250 km·h-14个等级下CRH3A气动噪声进行仿真，分析了各测点近场噪声随速度变化的规律。

表3为该点最大的A计权声压级。由表3可知，随着列车运行速度的提高，测点4噪声随速度增加而显著增加。

表3 测点4不同速度下的最大A计权声压级Tab.3 SPL comparison of probe 4 at different velocity

通过对其它测点分析，发现上述规律并不是普遍的。表4为受电弓底罩板上游区域某测点的最大的A计权声压级。表4表明，该测点噪声声压级在不同速度下总体上相差不大，没有明显的线性关系。这主要是因为该测点紧挨受电弓导流罩前缘底面，不同来流速度下，气流在该位置的速度很低，接近于零，因而同速度看不出明显的关系。

表4 导流罩上游区域测点不同速度下的最大A计权声压级Tab.4 SPL comparison of probes located at the up stream of dome at different velocity

3 总结

1）在受电弓下游区域的3个导流罩均为略微高强度的湍动能所覆盖，说明该区域可能成为重要的气动噪声源。

2）在受电弓的上框架、滑板等位置迎风侧均出现了滞止高压，并对来流造成一定扰动。

3）远离列车壁面测点的气动噪声，受列车运行速度影响显著，而贴近列车壁面的测点，由于处于列车下游区域，噪声随速度变化特性不明显。

[1] MELLET C,LETOURNEAUX F,POISSON F,et al.High speed train noise emission:latest investigation of the aerodynamic/rolling noise contribution[J].Journal of Sound and Vibration,2006,293:535-546.

[2] 孙振旭,宋婧婧,安亦然.CRH3高速列车气动噪声数值模拟研究[J]北京大学学报:自然科学版,2012,48(5):1-11.

[3] TALOTTE C,GAUTIER P E,THOMPSON D J,et al.Identification,modelling and reduction potential of railway noise sources:a critical survey[J].Journal of Sound and Vibration,2003,267:447-468.

[4] 张军,黄艳艺,兆文忠.高速列车气动噪声数值仿真[J].大连交通大学学报,2012,38(4):1-4,20.

[5] 郑拯宇,李人宪.采用计算气动声学研究高速列车表面偶极子声源外辐射的指向性[J].现代制造工程,2012(6):42-46.

[6] FFOWCS WILLIAMS J E,HAWKINGS D L.Sound generation by turbulence and surfaces in arbitrary motion[J].Philosophical transations of royal society of london,1969,264:321-342.

[7] 宋文萍,余雷,韩忠华.飞机机体气动噪声计算方法综述[J].航空工程进展,2010,2(1):125-131

[8] FARASSAT F,BRENTNER K S.The derivation of the Gradient of the acoustic pressure on a moving surface for application to the Fast Scattering Code(FSC)[C]//NASA/TM-2005-213777,2005.

[9] 张兆顺,崔桂香,许春晓.湍流理论与模拟[M].北京:清华大学出版社,2005:215-217.

[10] BATTEN P,RIBALDONE E,CASELLA M,et al.Towards a generalized non-linear acoustics solver[R].10th AIAA/CEAS Aeroacoustics Conferences,2004:2004-3001.