基于集合竞价置换的双向动态频谱分配算法

刘觉夫，胡 静，杨 将，朱丙虎

（华东交通大学信息工程学院，江西 南昌330013）

在无线电通信网络中，可用的频谱资源非常有限。目前广泛采用基于授权的频谱资源固定分配策略，将无线频谱划分成若干个固定宽度的频谱段，由政府管理部门分配给授权用户独占使用［1］，这种方法严重制约了频谱利用率。认知无线电使无线通讯设备具有发现闲置频谱资源的能力，并合理的配置资源，从而有效地提高频谱使用效率，从根本上解决日益增长的无线通信需求与有限的频谱资源之间的矛盾［2］。

针对动态频谱分配问题，国内外专家学者对双向频谱拍卖模型进行了广泛研究。文献［3］中Wang等人分别在统一价格和差异价格的条件下，设计了基于双向拍卖的市场局部性频谱拍卖机制，实现了买方和卖方的优化组合。文献［4］中Wu等人对已有的双向拍卖模型做出了进一步改进，提出了WTA双向拍卖算法，提高了频谱利用率并保证了拍卖参与者的真实性。文献［5］中Yao等人针对竞争者虚假报价的问题，建立了TDSA双向拍卖模型，保证了拍卖结果的真实性。文献［6］中Feng等人提出了基于异构频谱的双向拍卖机制TAHS，使认知用户能够准确的表达其对频谱的个人偏好，并且很好地解决了干扰图变化的问题。结合IEEE802.11e中无线局域网中一种提高QoS的算法［7］，文献［8］中Huang等人针对拍卖双方不同的买卖需求设计了多用户的双向拍卖方案，构造竞价相关的认知用户组并确定拍卖的赢家策略。文献［9］中Zhou等人提出了能够满足所有经济性能的TRUST机制，采用随机构成买方集合的方式，使在同一集合中的买方共同使用一个频段，实现了频谱的空间复用。

虽然以上算法都能够完成频谱分配的任务，但其忽视了拍卖参与者的个体理性和拍卖公平性，使拍卖陷入了一味追求收入最大化的误区。为满足认知用户的个体理性，保证拍卖的公平性，提高拍卖收益和频谱成交率，本文提出了基于集合竞价置换的双向动态频谱分配算法，并对其进行了理论分析和数值仿真。

1 双向拍卖模型

双向拍卖是一种“多对多”的拍卖结构，有多个买方和卖方，符合双边市场次级频谱拍卖的特点。因此，本文采用双向拍卖模型。

考虑认知无线网络场景包含1个代理商，m个主用户P={p1，p2,…，pm} 和n个次用户S={s1，s2,…，sn}。拍卖过程以密封竞价的方式进行，所有的参与者都采用密封的方式向代理商提交报价。由于实际情况中授权频谱覆盖率远远高于认知用户，因此主用户提供的信道能够被多个互不干扰的认知用户共享。系统模型如图1所示。

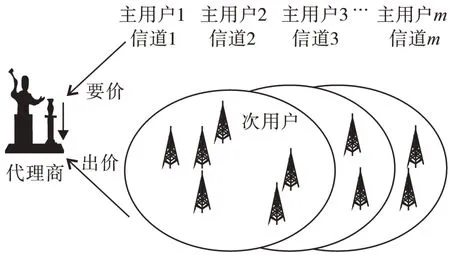
图1 双向拍卖系统模型Fig.1 System model of double auctions

主用户作为提供频谱的卖方，认知用户作为需要频谱的买方。假设每个卖方一次只提供一个待售信道，每个买方每次只需占用一个信道。卖方的出价与买方的要价分别表示为每个卖方pj向代理商提交一个价格aj，若买方出价低于aj，代理商将不租赁信道。而每个买方si向代理商提交一个价格bi，若卖方要价高于bi，买方将放弃竞价。

将卖方的分配矩阵记为X∈{0 ,1}m，若xi=1，则卖方pi赢得拍卖，且从拍卖商处获得pis。否则pi输掉拍卖，且pis=0。买方的分配矩阵记为Y={0 ,1}n×m，若yik=1，则买方si赢得卖方pk的频谱，并从拍卖商处获得pbi。否则yik=0，且pbi=0。矩阵X与Y需满足三个条件：①若si,sj∈εh，则yik+yjk≤1；②对任意一个买方si，；③对任意一个卖方pi，当且仅当时，xk=1。第1个条件表示，若两个买方位于同一个干扰集合，将不会被分配同一个信道。第2个条件表示一个买方最多只会被分配一个信道。第3个条件确保被分配信道的数量与拍卖赢家的数量相同。

假设每个卖方在其信道上拥有的成本为cj，每个买方在任意一个信道上所产生的收益为ri，且买方和卖方拥有相同的时间间隔。则卖方和买方的效用函数分别为

追求最大拍卖商收益Aopt的频谱分配问题可以用最优化模型描述如下

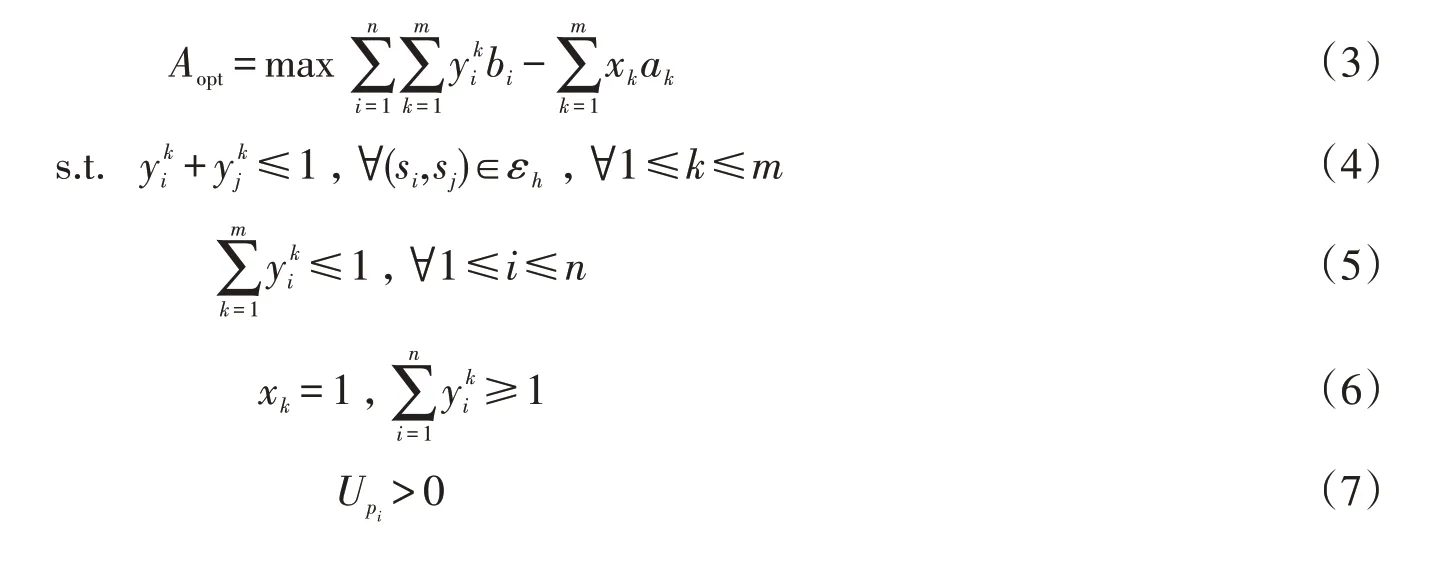
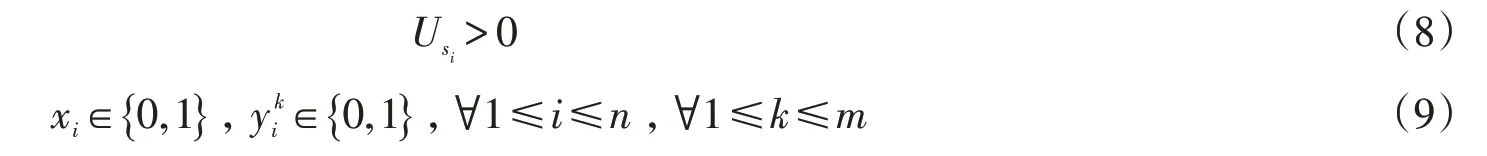
这是单目标的0-1规划问题，采用单纯形法进行求解。

1.1 买方集合划分

代理商通过测量认知用户之间的累计干扰度degree 来获得买方干扰关系图，将得到的图记为Gr，r∈(1,l)。在买方独立竞价的基础上，代理商采用measurement-calibrated propogation［10］模型，将有强干扰的买方分配在同一个子集中，将无干扰或弱干扰的买方分配在另一个子集中。由于买方之间的无线干扰情况被抽象为一个干扰集，为了提高独立集合构造能力，采用谱聚类算法［12］解决这个NP难题。将划分好的集合记为εh，h∈(1,t) ,t≤n。

1.2 双向拍卖-SBPA算法

将被划分形成的买方集合看作一个整体出价，在文献［9］中，定义了最优的买方集合出价，如下

但是按照公式（10）计算出的最优集合出价，并不满足个体理性。

假设频谱分配问题的最优化解为A，具有较优的β-竞争性［10］满足，A≥Aopt/β，且能保证个体理性。不妨假定卖方的要价为a={1.9,1.2,0.9,0.5}，买方的出价为b1=0.9，b2=b3=0.7，b4=0.6，b5=0.4，b6=0.2，b7=0.1。其中，b1,b6∈ε1，b2,b4,b5∈ε2，b3∈ε3，b7∈ε4。则由式（10）可得π1*=0.3，π2*=1.2，π3*=0.7，集合ε2的出价π2* 最大，赢得拍卖。显然，集合ε1中s1的出价为0.9，是三个集合中出价最高的买方，却还输掉了拍卖。不仅违背了拍卖的公平性，而且减少了拍卖收益。

针对该问题，本文提出了SBPA 集合竞价算法。在频谱拍卖过程中，买方除了向代理商提交出价外，还需提供其期望收益ri。

首先，代理商由式（10）计算出每个买方集合的最优集合出价πh*。若存在买方期望收益ri大于买方集合中的平均期望收益ri≥R/ ||εh，则集合中小于平均期望收益的买方赢得拍卖，并将这个期望收益作为买方交给代理商的初始出价pbi*。

然后，算法选择将集合价格为πi* 的集合映射到集合价格更优的πj* 集合上，其中πi*＜πj*，且i,j∈(1,t)。算法采用一个随机的排列置换c(r)={c(1),c(2),c(3),…,c(|bj|)|c(r)≠r}，将不同的集合进行置换。若大于置换前的集合出价，则置换成功，否则置换失败。在置换失败的集合中的买方将会被剔除。在置换成功的集合中，每个买方在其所在集合中平均地承担置换后的集合价格。

在确定赢得拍卖的集合与拍卖双方的真实出价后，对每个集合中赢得拍卖的买方按照其出价进行排序，并按卖方的真实出价顺序为其分配频谱，得到每个集合中的频谱分配结果集合winners。考虑到不同图之间的不连接性，需要将不同集合中的结果合并。合并过程中，每次选取两个图，找到每个图中累计干扰度最小的买方。如果这两个买方被分配到相同的信道，则将出价低的买方剔除，否则直接合并，得到最终的分配结果。

具体的算法流程如下：

2 实验仿真

使用Matlab2010软件平台进行仿真，仿真结果均由算法重复运行50次并计算其平均值而获得。参与拍卖的双方采用均匀分布方案（Uniform），随机的分配在1 000 m×1 000 m的范围内。若两个买方之间的距离小于300 m则产生干扰。为了验证本文提出算法的有效性，将其与TRUST作了比较。仿真参数设置如下表：

表1 仿真参数Tab.1 Simulation parameters

2.1 拍卖双方的成交情况

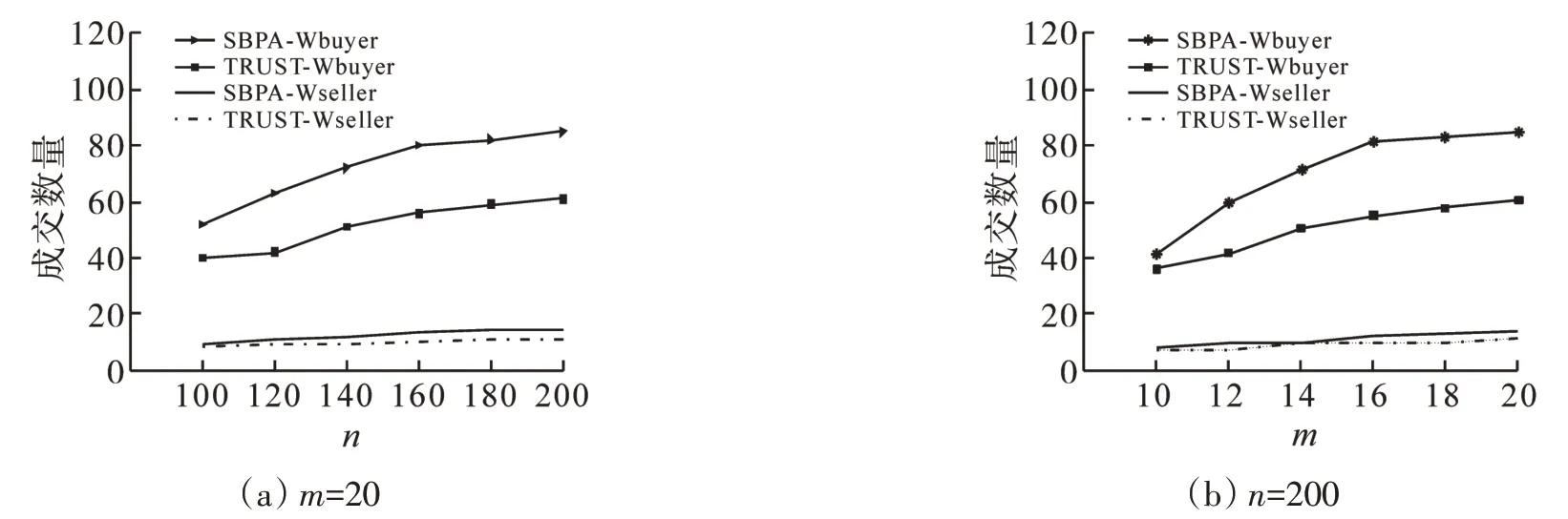
图2 成交用户数量随参与用户数量的变化关系Fig.2 Changes of the number of winning users along with the number of participants

如图2，以买方和卖方的成交数量作为对比。Wseller 表示赢得拍卖的卖方，Wbuyer表示赢得拍卖的买方。从图中可以看出，不管是TRUST 还是SBPA，随着参与者的增加，SBPA 算法的平均成交数量都大于TRUST。因此，SBPA算法能够显著地提高拍卖的成交量。

2.2 β-竞争性仿真及分析

为了度量拍卖的效果，本文引入了文献［12］中β-竞争性拍卖的概念：如果一个拍卖至少达到最优拍卖的1β，则这个拍卖是β-竞争性的，即A(a,b)≥Aopt/β。为了方便表示，令1/β=α。

从图3中可以看出TRUST算法和SBPA算法的β-竞争性都随着参与者数量的增加而增加。但SBPA最高可达到最优拍卖的1/2，而TRUST 在最优情况下都未能达到最优拍卖的1/3。因而，SBPA 算法具有较优的β-竞争性。

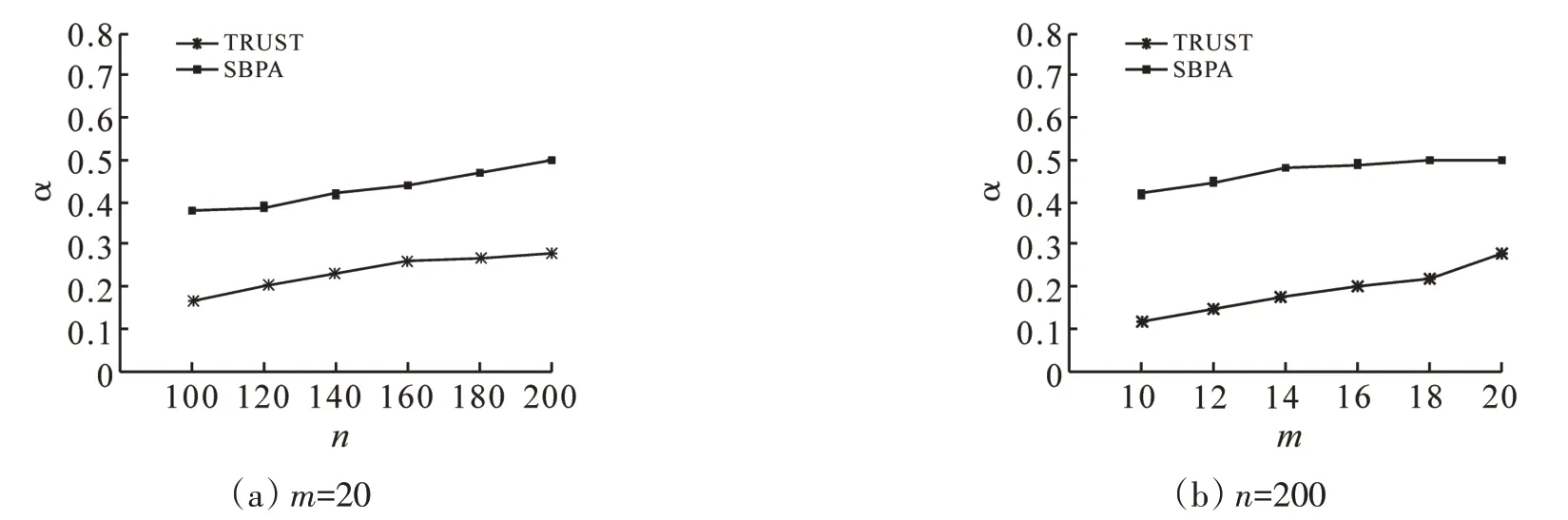
图3 β-竞争性随用户数量的变化关系Fig.3 β-competitive changes with the number of participants

2.3 拍卖收益仿真

针对拍卖收益，分别采用Uniform与Cluster分布方案进行仿真，收益变化关系如图4所示。Cluster方案选取中心买方，使其他的买方均匀随机的分布在距离中心买方（Cluster）100 m的范围内。

图4 两种买方分布下拍卖收益随买方分布情况的变化关系Fig.4 Revenue changes with two buyer distributions

3 结束语

本文基于认知无线网络，引用双边市场模型，利用双向拍卖理论，提出了基于集合竞价置换的双向动态频谱分配算法。为减少算法复杂度，使买方以集合的形式参与竞价。在拍卖过程中，由集合竞价置换算法计算出买方集合的出价及拍卖双方的真实出价后，由代理商为买方与卖方的出价进行排序并确定拍卖结果，最终在买方和卖方之间划分多对一的映射关系。理论分析证明，该算法能够在充分保证个体理性的基础上实现动态频谱分配。

仿真实验结果证明，该算法能够有效地提高拍卖成交率和拍卖收益，且具有较优的β-竞争性。在拍卖参与双方增多的情况下，可获得更优的拍卖结果。

[1] PAWELCZAK P, NOLAN K, DOYLE L, et al.Cognitive radio: Ten years of experimentation and development[J].Communications Magazine,IEEE,2011,49(3):90-100.

[2] WANG B,LIU K J R.Advances in cognitive radio networks:A survey[J].Selected Topics in Signal Processing,IEEE, 2011,5(1):5-23.

[3] WANG W, LI B C, LIANG B.District: Embracing local market in truthful spectrum double auction[C]//Proc of the 8th Annual IEEE Conf on Sensor,Mesh and Ad Hoc Communications and Networks(SECON 2011).Piscataway,NJ:IEEE,2011:521-529

[4] WU G,REN P,ZHANG C.A waiting-time auction based dynamic spectrum allocation algorithm in cognitive radio networks[C]//Global Telecommunications Conference(GLOBECOM 2011),2011 IEEE.IEEE,2011:1-5.

[5] YAO E, LU L, JIANG W.An efficient truthful double spectrum auction design for dynamic spectrum access[C]//Cognitive Radio Oriented Wireless Networks and Communications (CROWNCOM), 2011 Sixth International ICST Conference on.IEEE, 2011:181-185.

[6] FENG X,CHEN Y,ZHANG J,et al.TAHES:Truthful double auction for heterogeneous spectrums[C]//INFOCOM, 2012 Proceedings IEEE.IEEE,2012:3076-3080.

[7] 汤文亮,李健.IEEE802.11e无线局域网中一种提高QoS的算法[J].华东交通大学学报,2008,25(5):63-66.

[8] HUANG H, SUN Y, XING K, et al.Truthful multi-unit double auction for spectrum allocation in wireless communications[J].Wireless Algorithms,Systems,and Applications,2012,75:248-257.

[9] ZHOU X,ZHENG H.TRUST:A general framework for truthful double spectrum auctions[C]//Proc of IEEE Infocom 2009.Piscataway,IEEE,2009:999-1007.

[10] ZHOU X, ZHANG Z, WANG G, et al.Practical conflict graphs for dynamic spectrum distribution[C]//Proceedings of the ACM Sigmetrics international conference on Measurement and modeling of computer systems.ACM,2013:5-16.

[11] CHAUDHURI K,GRAHAM F C,TSIATAS A.Spectral clustering of graphs with general degrees in the extended planted partition model[C]//COLT.2012:35.1-35.23.

[12] CHEN N, GRAVIN N, LU P.Optimal competitive auctions[C]//Proceedings of the 46th Annual ACM Symposium on Theory of Computing.ACM,2014:253-262.