一种基于无双线性对映射的无证书代理签密方案

查文刚

（华东交通大学现代教育技术中心，江西 南昌330013）

Al Riyami和Paterson 2003首次提出无证书密码体制［1］，给出了无证书公钥密码系统的概念同时并提出了首个无证书签名方案。这种签名方案的部分秘钥是由用户和KGC共同协议产生，解决了基于身份的密码系统中的密钥托管问题，提高了效率。1997年Zheng首次提出的签密［2］的概念，能同时完成签名和加密，在计算量和成本上，远远低于传统的先签名后加密的密码体制缺点是不满足公开验证性。Bao针对公开验证性分别给出了改进的可公开验证的签密方案［3］，Shin指出文献［3］的方案不满足语义安全，并给出了改进方案［4］。随后不少研究者在此基础上提出了不少高效的签密方案及其变种［5-9］。

代理签密是由Gamage于1999年首次提出，Gamage等人提出的代理签密方案，实现了一个代理签密人代替原始签密人进行签密，但此方案没对安全性进行证明［10］。2004年，Li提出了一种基于身份的代理签密方案［11］，然而，Wang指出文献［10］的方案不具有不可伪造性和前向安全性，并给出了改进的方案［12］。无证书代理签密可以结合无证书签密和代理签名的特点，不存在密钥托管问题，而且不需要证书来认证公钥，安全性高，效率高。所以，无证书代理签密在实际工程中中应用更广泛。2009年，王会歌提出的高效的无证书可公开验证签密方案，安全性存在问题，方案不能抵抗公钥替换攻击，而且运用了双线性对运算，计算效率低［12］。2010年，Yu提出了一种基于椭圆曲线上的无证书代理签密方案，这个方案简单可行，但是安全性不高［14］。本文在文献［15］的基础上提出了一种基于无双线性对映射的无证书代理签密方案，整个方案只运用了加法和乘法运算，大大的减少了算法的计算量和通信成本，易于在移动通讯的敏感数据交换技术中应用。

1 预备知识

定义1（离散对数困难问题假设）设G是阶为q的一个加群，P为G的生成元，对于任意的a∈Zq*，已知aP，P，计算a是离散对数问题，在概率多项式时间（PPT）内，对于任意攻击算法Α，在解决DLP困难问题的优势AdvDLP(Α)=Pr[Α(uP,P)=u|u∈Z*q]是可忽略的。

2 基于无双线性对映射的无证书代理签密方案

2.1 参数选取和密钥生成

KGC利用有效算法L(1k)，生成参数(G,q,P)，其中G为具有素数阶q的循环群（以下不加说明默认为椭圆曲线群）。选择安全hash 函数：H1:{0,1}*×G×G×G→Z*q，H2:G×→Z*q，H3:{0,1}*×G→Z*q，H4:{0,1}*×{0,1}*×G×G×G×G→Z*q，H5:{0,1}*×{0,1}*×{0,1}*×G×G→Z*q。

KGC选择xkgc作为其主私钥，计算其主公钥ykgc=xkgcP。

假定用户Ai的身份为IDi（可以是用户私人相关有效信息），Ai随机选择一个xi∈Z*q作为自己的长期私钥（以下简称私钥），计算yi=xiP作为其长期公钥（以下简称公钥）。将yi发给密钥生成中心KGC。Ai将(IDi,yi)发送给KGC申请另一部分密钥。

KGC秘密选择随机数ui,vi∈Z*q，计算：

作为Ai的另一部分私钥（以下简称部分私钥），将公开作为Ai的另一部分公钥（以下简称部分私钥）。KGC 将通过安全可靠渠道发送给用户Ai。于是用户Ai完整私钥为，完整公钥为

2.2 委托过程

假设Alice对Bob进行委托，Alice的身份为IDA，完整私钥为(xA,)，完整公钥为(yA,,UA,VA)，Bob的身份为IDB，完整私钥为(xB,)，完整公钥为(yB,,UB,VB)。

1）Alice 随机选取秘密值k1,k2∈Z*q，计算K1=k1P，K2=k2P，并计算：e1=H2(K1,K2)，e2=H2(K2,K1)，w=e1xA+e2+k，W=wP将K1、K2和W发送给Bob，w通过安全信道发送给Bob。

2）Bob 计算e′1=H2(K1,K2)，e′2=H2(K2,K1)，验证等式，若不成立，拒绝Alice的委托，若成立，则计算代理签名密钥，公开其对应公钥y=xP。

2.3 代理签密的生成过程

代理签密的参与者为Bob 与Cock，Bob 的身份为IDB，完整私钥为(xB,)，完整公钥为(yB,,UB,VB)，代理签名密钥x，对应公钥y。Cock的身份为IDC，私钥为(xC,)，公钥为(yC,,UC,VC)。需传递数据信息为m，数据信息加密采用安全对称加密算法（记加密过程为Ekey，解密过程为Dkey）。Bob随机选择对称密钥key∈Zq*，加密后得到密文s=Ekey(m)，计算M=H3(m)。

1）随机选取t∈Zq*，计算T=tP，K=key⊕H5(IDA,IDB,IDC,(x+t)(yC+),T)。

2）计算s=t(x+h)-1，h=H4(IDB,IDC,K,M,T,K1+K2)。

将S=(h,s,T,K,M,K1,K2)作为签密数据发送给Cock。

2.4 代理签密的签名验证和解密过程

2.5 代理签名的注销过程

Alice向签名用户广播一条消息，声明任何含有(K1,K2)的签密数据S=(h,s,T,K,M,K1,K2)为无效信息。

3 安全性与效率分析

3.1 方案正确性

1）代理密钥生成过程的正确性

接收者收到(K1,K2,w)之后验证下列式子

2）解签密过程的正确性

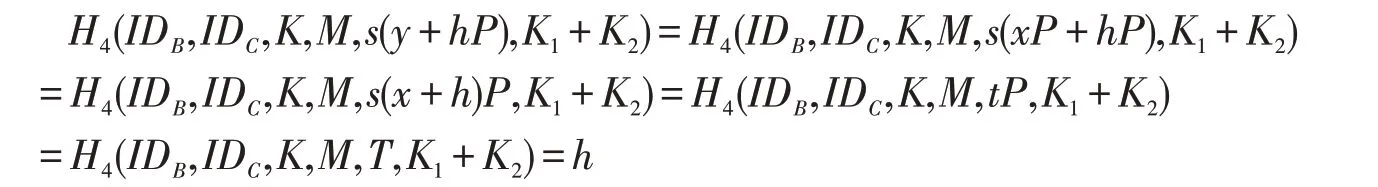
3.2 随机预言机下可证安全性

本文方案包括一个原始签密者、一个代理签密者和签密接受者，签密方案包括以下过程：系统参数的选取，密钥的生成，委托过程，代理签密的生成，代理签密的签名验证和解密，代理签密的注销。对于无证书的签密方案都存在两种类型的攻击者：（类型1）攻击者Q1无法获知系统的主密钥，但是可以替换任意用户的长期公钥；（类型2）攻击者Q2不能替换用户的公钥，但可以获得系统的主密钥。

由于类型2的攻击更具有破坏力，攻击成功则影响所有用户，本文只证明对类型2攻击下是可证安全的，对于类型1的证明过程基本类似（只是询问过程有些不同，证明过程也可参考文献［15］中的定理2和定理3）。

定理1（类型2攻击下的不可伪造性）在随机预言机模型和第二类攻击假设下，若存在算法Q在多项式时间t内，通过进行有限多项次询问，以不可忽略的概率ε伪造一个有效的签密，那么存在一个挑战者Ω在多项式时间t′内，以不可忽略的概率ε′解决ECDLP。

证明已知y=xP∈G，为了计算x（x为用户ID*的长期私钥），x∈Zq*，假设挑战者Ω 为求解x，将算法Q作为自己的子程序，并与攻击者算法Q进行游戏交互，且在多项式时间内最多允许攻击者算法Q执行qH1次H1询问、qH2次H2询问、qH3次H3询问、qH4次H4询问、qH5次H5询问、qBM次部分密钥提取询问、qSK次长期私钥提取询问、qPK次长期公钥提取询问、qDK次代理密钥提取询问、qQM次代理签密询问、qJM次解密询问。挑战者Ω 维持列表LH1，LH2，LH3，LH4，LH5，LBM，LLK，LDK，LQM，LJM分别用于应对H1询问、H2询问、H3询问、H4询问、H5询问、部分密钥提取询问、长期密钥提取询问、代理密钥提取询问、代理签密询问、解密询问，并初始化所有列表为空。

挑战者Ω 生成系统参数param=｛G，q，P，H1，H2，H3，H4，H5，ykgc｝并将系统参数发送给攻击者。挑战者Ω 随机选择xkgc∈Zq*作为KGC私钥，KGC公钥为ykgc=xkgcP。C随机选取k,0 ≤k≤qPK1，身份标示ID*=IDk，对应的用户长期公钥为yk=xkP，用xk来模拟IDk的长期私钥。显然询问过程不能询问ID*的长期私钥。

3.2.1H1询问

当挑战者Ω 收到攻击者Q关于H（1IDi,Ui,Vi,yi）的H1询问，Ω 首先查询列表LH1，如果（IDi,Ui,Vi,yi,h1i）存在于列表LH1中，则Ω 将h1i返回给Q；否则，Ω 随机选择h1i∈Zq*，将其作为回答返回给Q1，并且将（IDi,Ui,Vi,yi,h1i）添加到列表LH1中。

3.2.2H2询问

当Ω 收到Q关于H（2K1i,K2i）的H2询问，Ω 首先查询列表LH2，如果（K1i,K2i，ei）在列表LH2中，那么Ω将ei返回给Q；否则，Ω 随机选择ei∈Zq*，将其作为回答返回给Q，并且将（K1i,K2i，ei）添加到列表LH2中。

3.2.3H3询问

当Ω 收到Q关于H3(mi)的H3询问，Ω 首先查询列表LH3，如果(mi,Mi)在列表LH3中，那么Ω 将Mi返回给Q；否则，Ω 随机选择Mi∈Zq*，将Mi作为回答返回给Q，并且将(mi,Mi)添加到列表LH3中。

3.2.4H4询问

当Ω收到Q关于H4(IDBi,IDCi,Ki,Mi,K1i+K2i) 的H4询问，Ω首先查询列表LH4，如果(IDBi,IDCi,Ki,Mi,K3i，h4i)在列表LH4中，那么Ω 将h4i返回给Q；否则，Ω 随机选择h4i∈Zq*，将其作为回答返回给Q，并将(IDBi,IDCi,Ki,Mi,K3i,h4i)添加到列表LH4中。

3.2.5H5询问

当Ω 收到Q关于H5(IDAi,IDBi,IDCi,Ei,Ti)的H5询问，Ω 首先查询列表LH5，如果(IDAi,IDBi,IDCi,Ei,Ti,h5i)在列表LH5中，那么Ω 将h5i返回给Q；否则Ω 随机选择h5i∈Zq*，将其作为回答返回给Q，并将(IDAi,IDBi,IDCi,Ei,Ti,h5i)添加到列表LH5中。

3.2.6 部分密钥提取询问

当Ω 收到Q关于(IDi,Ui,Vi)的询问，Ω 首先查询列表LBM，如果在表LBM中，那么Ω 将相应的值发送给Q；否则Ω 先运行H1询问提取h1i，随机选择ui，vi∈Zq*，计算Ui=uiP,Vi=viP，，将记录到列表LBM中，将返回给Q。

3.2.7 长期私钥提取询问

当Ω 收到Q关于IDi的私钥提取询问，Ω 先检查列表LLK。若(IDi,xi,yi)在列表LLK中，那么Ω 将相应的xi发送给Q；否则

1）当i≠k时：Ω 先做关于IDi的H1询问，然后再执行部分私钥提取询问得到x¯i，随机选择xi∈z*q，计算yi=xiP。把(IDi,xi,yi)添加到列表LLK，将相应的xi发送给Q；

2）当i=k时：算法停止。

3.2.8 长期公钥提取询问

当Ω 收到Q关于IDi的公钥提取询问，Ω 先检查列表LLK。如果(IDi,xi,yi)在列表LLK上，则Ω 将yi发送给Q；否则

1）当i≠k时：随机选择xi∈Zq*，计算yi=xiP把(IDi,xi,yi)添加到列表LLK，将yi发送给Q；

2）当i=k时：而用户私钥用⊥表示，公钥为yk，将yk发送给Q，并且将(IDi,⊥,yk)添加到列表LLK。

3.2.9 代理密钥提取询问

当Ω 收到Q关于(IDAi,IDBi)的部分代理密钥询问，若(IDAi,IDBi,k1i,k2i,K1i,K2i,Wi,xpi,ypi)在列表LDK中，则返回(xpi,ypi) 给Q；否则当IDAi≠IDk且IDBi≠IDk时：Ω 随机选取秘密值k1i,k2i∈Z*q，计算K1i=k1iP，K2i=k2iP，接着执行H2询问获取e1i,e2i，部分密钥提取询问获取和，长期私钥提取询问获得(xAi,xBi)和长期公钥提取获得(yAi,yBi)，然后计算：Wi=wiP。同时将(IDAi,IDBi,k1i,k2i,K1i,K2i,Wi,xpi,ypi)记录到列表LDK中，将(xpi,ypi)返回给Q。

3.2.10 代理签密询问

当Ω 收到Q关于(IDAi,IDBi,IDCi)和mi的代理签名询问，查询列表LJM，若在列表LJM中已经存在记录(mi,IDAi,IDBi,IDCi,h4i,si,Ti,Ki,Mi,K1i,K2i) ，则返回(hi,si,Ti,Ki,Mi,K1i,K2i) ，Ω 运行代理密钥提取询问得到(K1i,K2i,xpi,ypi) ，运行H3询问获得Mi，运行H4询问获得h4i，运行H5询问获得h5i，随机选择ti∈Z*q，keyi∈Zq*，计算T=tp，Ki=keyi⊕h5i，si=ti(xpi+h4i)-1，得到(mi,IDAi,IDBi) 的签密(h4i,si,Ti,Ki,Mi,K1i,K2i) ，将σ=(h4i,si,Ti,Ki,Mi,K1i,K2i)发送给Q，并将(mi,IDAi,IDBi,IDCi,h4i,si,Ti,Ki,Mi,K1i,K2i)添加到LJM。易验证若算法不终止，签密信息可以通过签名和验证。

3.2.11 解签密询问

当Ω 收到Q关于(IDAi,IDBi,IDCi)的一个签密(h4i,si,Ti,Ki,Mi,K1i,K2i)时，查询列表LJM，若在列表LJM中已经存在记录(mi,IDAi,IDBi,IDCi,h4i,si,Ti,Ki,Mi,K1i,K2i)，则返回mi给Q，否则

1）当IDCi≠IDk：Ω 首先根据签密者和接收者的身份以及公钥从列表LH4中查询h4i，若在LH4查找出匹配的h4i，验证查找出的h4i与接收到的h′4i是否相等，如果不相等，则拒绝对(h4i,si,Ti,Ki,Mi,K1i,K2i)解签密；若相等，则Ω 从列表LBM和LLK中查找出IDCi的完整私钥(xCi,)，若在LH5查找出匹配的h5i，计算keyi=Ki⊕h5i，执行解密算法即可得到m。

2）当IDCi=IDk：Ω 首先根据签密者和接收者的身份以及公钥查询列表LH4，若在LH4不存在匹配的h4i，则终止协议；若能在LH4查找出匹配的h4i，并验证查找出的h4i与接收到的h′4i是否相等，如果不相等，则拒绝对(h4i,si,Ti,Ki,Mi,K1i,K2i)解签密；如果相等，那么Ω 查询列表LH5，查找出h5i，执行以下算法：

①α=1；

②若α＜qH5，则在列表LH5中查询出h5α，计算key=K⊕h5α，用这个key和所接收到的s来解密，即mα=Dkey(s)；

③查询列表LH3，若存在(mα,Mα)，则返回mα，否则执行④；

④α=α+1，执行②。

最后Ω 将输出的mα发送给Q。

Q进行至多有限次多项式次询问后，在概率多项式时间t内，以不可忽略的概率ε，产生一个有效的签密数据。设代理签名密钥x，对应公钥y，利用分叉规约技术对H4进行分叉，根据分叉引理，通过对Q的哈希重放，Ω 可以得到消息m的两个有效的签密信息：S=(h,s,T,K,M,K1,K2)和S′=(h′,s′,T,K,M,K1,K2)。

由s(y+hP)=s′(y+h′P)退出s(x+h)=s′(x+h′)，计算可得，因此求解了离散对数问题y=xP。

以下我们给出算法Ω 成功的优势和执行的时间粗估计（精细估计方法可参考文献［15］）：对于没有询问过程算法没有停止的概率至少为，成功伪造签密的概率至少为，因此，算法Ω 成功的优势，假设tH1，tH2，tH3，tH4，tH5，tBM，tSK，tPK，tDK，tQM，tJM分别为H1询问，H2询问，H3询问，H4询问，H5询问，部分密钥提取询问，长期私钥提取询问，长期公钥提取询问，代理密钥提取询问，代理签密询问，解密询问一次所需时间，算法Ω 执行完成的时间t′满足

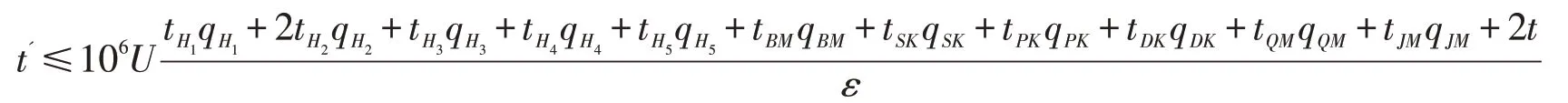
通过以上分析，Ω 能在概率多项式时间t′内，以不可忽略的概率ε′，解决y=xP求出x。这与离散对数问题的困难性矛盾，所以针对类型2攻击本文方案具有不可伪造性。

4 效率以及与其它方案的性能比较分析

本文方案不需要双线性对运算和指数运算，签密运算和解签密运算只进行椭圆曲线上的数乘运算，文献［12］运用了双线性对运算，目前快速双线性对运算时间是椭圆曲线上点乘所需时间的20倍左右，因此效率与本文的方案相比要低。而文献［14］虽然是基于无双线性对映射的，但是运用了指数运算，而且其为了保证方案的前向安全性，其代理授权过程计算量比较大，效率并不高。我们用H 表示哈希函数运算，用M表示椭圆曲线上的数乘运算，E 表示指数运算，P 表示双线性对运算，具体的方案效率分析及比较见表1。

表1 与其它方案的性能比较Tab.1 Comparison of efficiency results between our scheme and other signcryption schemes

5 结论

1）本方案没有运用双线性对运算和指数运算，能够抵抗公钥替换攻击，在随机预言机模型中，方案对于适应性选择消息攻击具有机密性和不可伪造性。

2）本方案在设计和实现上借鉴了国密SM2标准签名方案的参数和技巧，计算开销明显低于其他方案，提高了方案的效率。

[1] AL-RIYAMI, PATERSON.Certi fi cateless public key cryptography[C]//Advances in Cryptology-ASIACRYPT 2003.Berlin:Springer-Verlag Berlin Heideberg,2003:452-473.

[2] YANG ZHENG.Digital signcryption or how to achieve cost (signature & encryption) [C]//Advances in Cryptology-CRYPTO′97.Berlin:Springer-Verlag Berlin Heideberg,1997:165-179.

[3] BAO F, DENG R.A signcryption scheme with signature directly verifiable by public key[C]//Advances in Cryptology-CRYPTO′98.Berlin:Springer-Verlag Berlin Heideberg,1998:55-59.

[4] SHIN J B,LEE K,SHIM K.New DSA-verifiable signcryption schemes[C]//Information Security and Cryptology-ICISC 2002.Berlin:Springer-Verlag Berlin Heideberg,2003:35-47.

[5] 汤鹏志,陈仁群,左黎明.一种基于椭圆曲线的门限部分盲签名方案[J].华东交通大学学报,2014,31(6):96-102.

[6] 左黎明,汤鹏志,刘二根.一种辫群上代理签名方案[J].计算机应用,2011,31(11),2979-2982.

[7] 左黎明,陈仁群,郭红丽.可证安全的基于身份的签密方案[J].计算机应用,2015,35(3):712-716.

[8] SHARMIL S D S,VIVEK S S,RANGAN C P.Cryptanalysis of certificateless signcryption schemes and an efficient construction without pairing[C]//Information Security and Cryptology.Berlin:Springer-Verlag Berlin Heideberg, 2011:75-92.

[9] LIU Z H,HU Y P.Certificateless signcryption scheme in the standard model[J].Information Sciences,2010(7):452-464.

[10] GAMAGE C, LEIWO J, ZHENG Y.An efficient scheme for secure message transmission using proxy signcryptio[C]//Proceedings of 22nd Australasian Computer Science Conference.Berlin:Springer-Verlag,1999:420-431

[11] LI XIANGXUE,CHEN KEFEI.Identity-based proxy signcryption scheme from pairing[C]//Proceedings of the IEEE International Conference on Services Computing(SCC2004).Berlin:Springer-Verlag Berlin Heideberg,2004:494-497.

[12] 王会歌,王彩芬,易玮,等.高效的无证书可公开验证签密方案[J].计算机工程,2009,35(5):147-149.

[13] 王琴.一种基于身份的代理签密体制[J].计算机工程,2011,37(19):120-121.

[14] 俞惠芳,王彩芬,王之仓.基于ECC 的自认证代理签密方案[J]计算机科学,2010,37(7):91-92.

[15] 文佳骏,左黎明,李彪.一个高效的无证书代理盲签名方案[J].计算机工程与科学,2014,36(3):452-457.