由一道题的错误解法想开去

朱斌

（镇江市丹徒高级中学 江苏镇江 212028）

由一道题的错误解法想开去

朱斌

（镇江市丹徒高级中学 江苏镇江 212028）

数学问题的难度和迷惑之处很大程度上是由于隐含条件、和审题不清导致。本文从一道错误的解答中，发现了类似于此的症结，对比自身的教学，归纳总结如何突破题目中的要害。

【1】作者李歆先生在证明一道数学奥林匹克选拔试题中，总结了一种关于利用设元和换元等常用数学方法，给出了一道题目的解答，笔者从李先生的解答过程中，发现一个错误，并由此想到了自己在平时的日常教学中，出现的类似的这样的问题，并作出总结、归纳

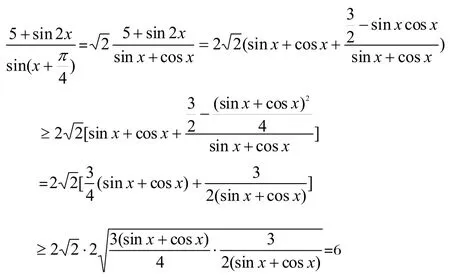
从以上的解答过程中，似乎并没有看出什么问题。可是仔细研究一下发现，令当时从数学分析的角度出发，当函数是连续函数时，未知量给定了一个有上下届的范围，则函数值也应该有上下届的—-即函数的取值应该有一个上下范围，而不是大于等6。笔者提供了两个解答，如下：

解题中很容易忽视 1-=x 这个解是错误的。

以上结果是否正确呢？从分类讨论的思想说是没有问题的，可是错误出现在什么地方呢？重新理解题意可以发现在上是可正、可负、可零的，当时有恒成立，a为全体实数。（隐含条件）

罗增儒先生在《数学审题审什么，怎么审》就指出：弄清问题是所有工作的第一步。【2】正所谓“成在审题、败在审题”。笔者认为，审题的步骤不仅仅在于题目本身，在解答过程中，特别是恒等变形、变量代换的过程中，也需要“审题”。每一个步骤，每一个式子，甚至每一个符号，都应该是我们需要关注的对象。在平时的教学中，笔者常常喜欢搞“翻译”：至少（之多）任意的---所有的等等。数学是抽象的，特别是有些数学概念，但是我们可以结合日常的生活例子、语言，以此与对题目的理解相结合，帮助学生掌握知识、提高解决问题的能力。

数学是一门思维科学，理性的思考和判断将有助于提高解决试题的应对能力。数学老师是一个“大家”，带领学生用生活的素材，来装扮数学的色彩！

［1］李歆.一道世界数学团队锦标赛试题的命制及其研究［J］.中学数学教学参考（上 旬），2012（4）：36-37.

［2］罗增儒.数学审题审什么，怎么审？.中学数学教学参考