A coupled immersed boundary-lattice Boltzmann method and its simulation for biomimetic problems
Jie Wu,Chng Shu∗
aDepartment of Aerodynamics,Nanjing University of Aeronautics and Astronautics,Nanjing 210016,China
bDepartment of Mechanical Engineering,National University of Singapore,Singapore
A coupled immersed boundary-lattice Boltzmann method and its simulation for biomimetic problems
Jie Wua,Chang Shub,∗
aDepartment of Aerodynamics,Nanjing University of Aeronautics and Astronautics,Nanjing 210016,China
bDepartment of Mechanical Engineering,National University of Singapore,Singapore
A R T I C L E I N F O
Article history:
Received 21 November 2014
Accepted 31 December 2014
Available online 14 February 2015
Immersed boundary-lattice Boltzmann method
A coupled immersed boundary-lattice Boltzmann method(IB-LBM)is introduced to solve biomimetic problems.Compared to the conventional IB-LBM,the strict satisfaction of no-slip boundary condition is implemented in the current method.Consequently,the phenomenon of flow penetration that is frequently observed in the conventional IB-LBM is fully prevented,and subsequently the force on the boundary can be calculated more accurately.This feature is ofimportance for the simulation ofbiomimetic problems.Moreover,by applying the relationship between the velocity correction and forcing term,the boundary force can be calculated easily.Several biomimetic problems are then simulated.Based on the good agreement between the current results and those in the literature,it may be concluded that the present IB-LBM has the capability to handle various biomimetic problems.
©2015 The Authors.Published by Elsevier Ltd on behalf of The Chinese Society of Theoretical and Applied Mechanics.This is an open access article under the CC BY-NC-ND license(http:// creativecommons.org/licenses/by-nc-nd/4.0/).
As typical moving boundary problems,biological and biomimetic problems are constantly observed in both nature and engineering applications.Some examples are bird/insect flight,fish swimming,and micro air vehicles(MAVs),and so on.Many ofthese applications involve unsteady flows together with complex configurations and moving boundaries.To numerically solve such problems,common approaches are to use either body-fitted meshes or fixed meshes.As compared to the former approaches that always require a frequent mesh regeneration process,the latter ones just use a regular fixed mesh for the discretization of flow field.Owing to such simplicity,they are very popular for biomimetic problems with arbitrary geometries.Thereinto,the immersed boundary method(IBM)introduced by Peskin[1]is a famous example.The basic idea of IBM is that the immersed boundary can be modeled by a series of Lagrangian points,and the body forces acting on the Lagrangian points that represent the effect of boundary can be distributed into the surrounding flow field.Subsequently,the whole flow field with discretization can be solved on a regular Cartesian mesh.
From the methodological point of view,the IBM can be regarded as a technique for boundary treatment.Meanwhile,the flow field solution can be obtained by either solving the traditional Navier-Stokes(N-S)equations or using other approaches.One choice is the lattice Boltzmann method(LBM)that is an alternative to N-S solver with high simplicity and parallelism,and it has achieved a great success for simulating various flow problems[2]. The coupling of IBMwith LBM(i.e.,IB-LBM)was first performed by Feng and Michaelides[3]and used to simulate particulate flows. Thereafter,this method has been refined continually and utilized to handle a variety ofmoving boundary problems[4-7].It is known that one key issue in IB-LBM is the calculation of forcing term. Currently,there are two ways to treat the forcing term,i.e.,explicit and implicit.In the explicit treatment that has been popularly employed,the forcing term is calculated in advance by using the penalty method[3],direct forcing method[4],or momentum exchange method[5].As a result,the no-slip boundary condition is only approximately satisfied,which may induce some flow penetration to rigid boundary.In the implicit treatment,on the other hand,the boundary force is first assumed to be unknown and then is obtained by solving a formed matrix directly[6]or applying the iteration procedure[7].During this process,the no-slip boundary condition can be satisfied accurately.Compared to the iteration procedure,it is shown that the direct method for solving the resultant equation system is more efficient.Meanwhile,the boundary force can be subsequently obtained.
In the framework of IB-LBM,the equations governing the twodimensional viscous and incompressible flow with the embedded body can be expressed as
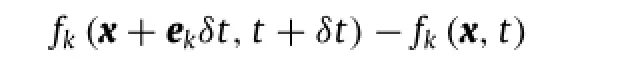
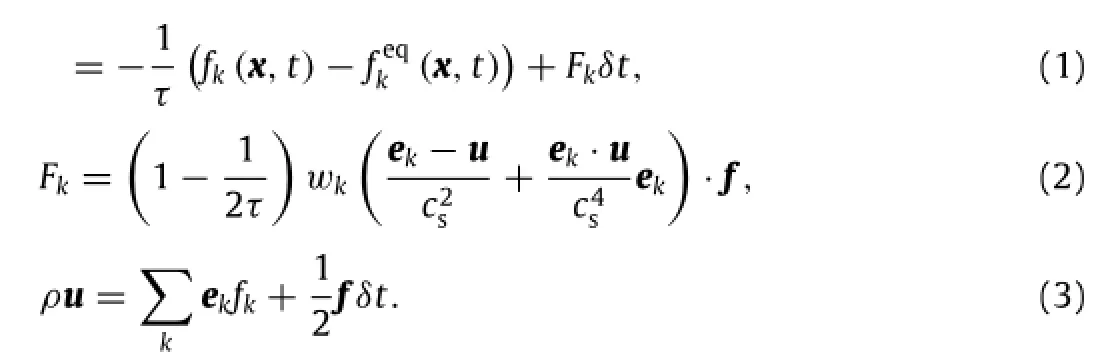
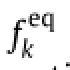
To satisfy the no-slip boundary condition,the force density f in Eqs.(2)and(3)is assumed to be unknown and resolved by enforcing the boundary condition[6].As a consequence,the force density f is determined by the fluid velocity correctionδu,which can be achieved from the boundary velocity correctionδuB.The final system of equations aboutδuBcan be written as

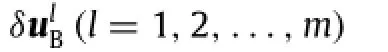
与传统旅游有所不同,红色旅游与生俱来带着浓厚的政治色彩,导游讲解时,要防止加入低级趣味或者迷信等方面的内容,要带着崇敬之心,认真对待革命历史,要按照严肃性以及严谨性原则,以合理态度对待红色旅游,从而对红色旅游色彩与基调进行保证。
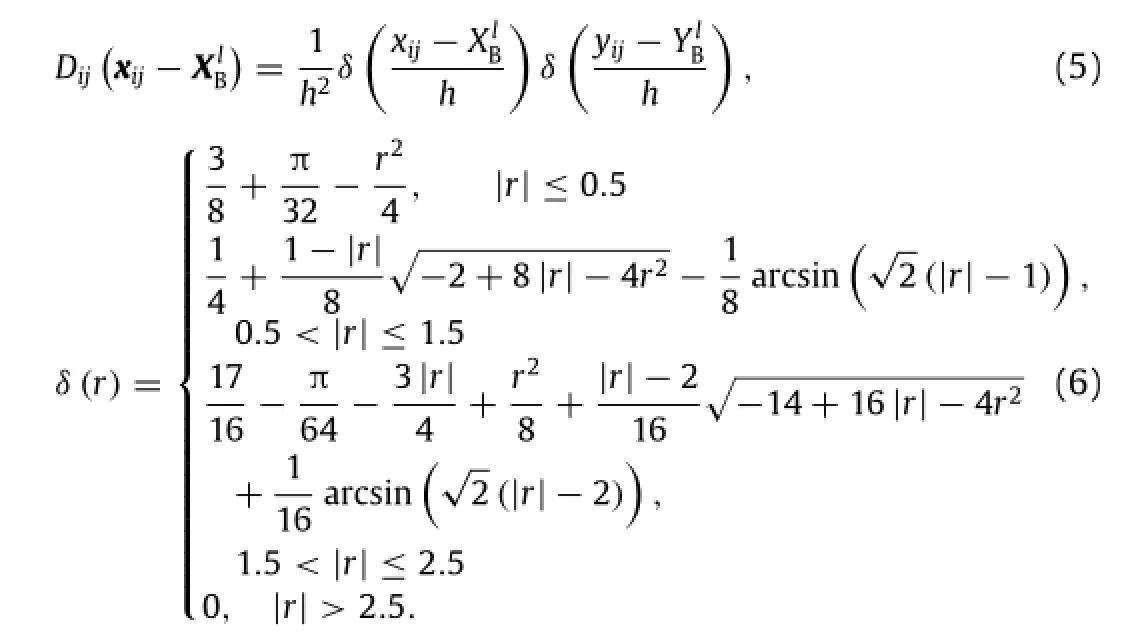



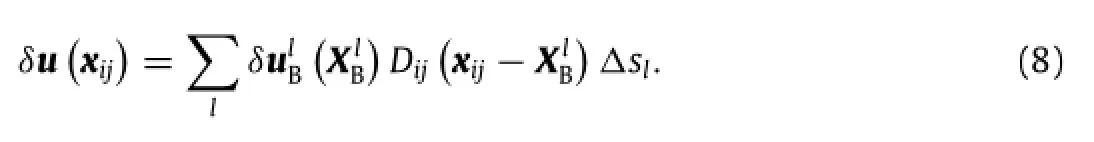
From Eq.(3),it is noted that the relationship between f andδu can be expressed as f=2ρδu/δt.Thus,the force on the boundary point can be similarly calculated from

This force is exerted on the fluid,which is balanced by the hydrodynamic force Ffon the boundary.In addition,other macroscopic variables in LBM are calculated by using the relationships

where csis the sound speed of the lattice model.
Compared to the conventional IB-LBM,the current method can exactly satisfy the no-slip boundary condition,which can improve the accuracy of solutions.Thus,the present IB-LBM can be applied to accurately deal with both the stationary and moving boundary problems.
The present IB-LBM has been well validated and used to simulatedifferentmovingboundaryflowproblems[9-11].Inthiswork,it is applied to handle some typical biomimetic problems.
Similar to the work of Gao and Lu[12],an ellipse foil with the thickness ratio of 0.25 is used to model the wing cross-section.The motion of the foil including translation and rotation is governed by
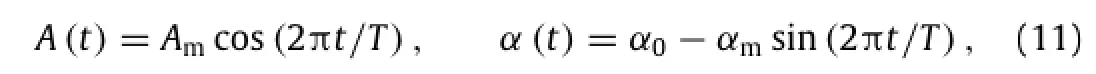
where T is the flapping period,Amis the amplitude of translation,α0andαmare respectively the mean angle of attack and amplitude of rotation.To represent the deformation of the foil,a fish-like sinusoidal motion mode is employed

where Bmis the amplitude of deformation andφis the phase difference between the translation and deformation.Same as the work of Gao and Lu[12],Am=1.25c,α0=90°,andαm=45°are used in the current simulation.The distance between the foil and groundisD=c.TheReynoldsnumber,whichisbasedonthechord length c and translation velocity U=2πAm/T,is Re=100.In addition,Bm=0.3c,φ=90°,andφ=-90°.The computational domainis40c×20c.Anon-uniformmeshcanbeused,inwhichthe meshfortheregionaroundthefoil(theregionsizeis2.4Am×1.2c)is uniform with the mesh spacing of h=1/80.
Figure1showsthetimehistoryofliftcoefficientsCLfortherigid and flexible foils during one flapping period.It is noted that the current result of the rigid foil shows reasonable agreement with that of Gao and Lu[12].From the figure,it is found that the flexibility of the foil can clearly influence the lift force on the foil.In this work,CLof the flexible foil is decreased atφ=90°and increased atφ=-90°compared to the rigid foil.Figure 2 presents the instantaneous vorticity contours for the rigid foil and the flexible foil withφ=-90°.As can be seen,the flexible foil weakens the vorticity interaction with the ground as it comes to the peakpositions of stroke(t/T=7/16 and t/T=11/16 in the figure). This behavior may explain the increase of the lift coefficient in Fig.1.
Besides hovering,the flapping wing also can generate thrust force to make the birds/insects move forward.Similarly,the flexibility canimprove the locomotion capability.Same as the work of Kinsey and Dumas[14],a NACA0015 airfoil is used to represent the wing cross-section.Its motion including plunge and pitch is governed by
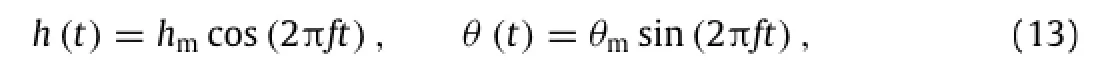
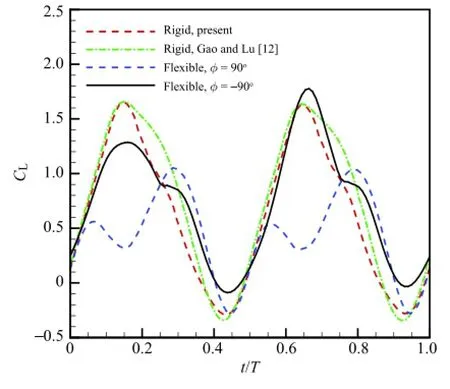
Fig.1.Time history of lift coefficients for the hovering rigid and flexible foils near the ground during one flapping period at Re=100.
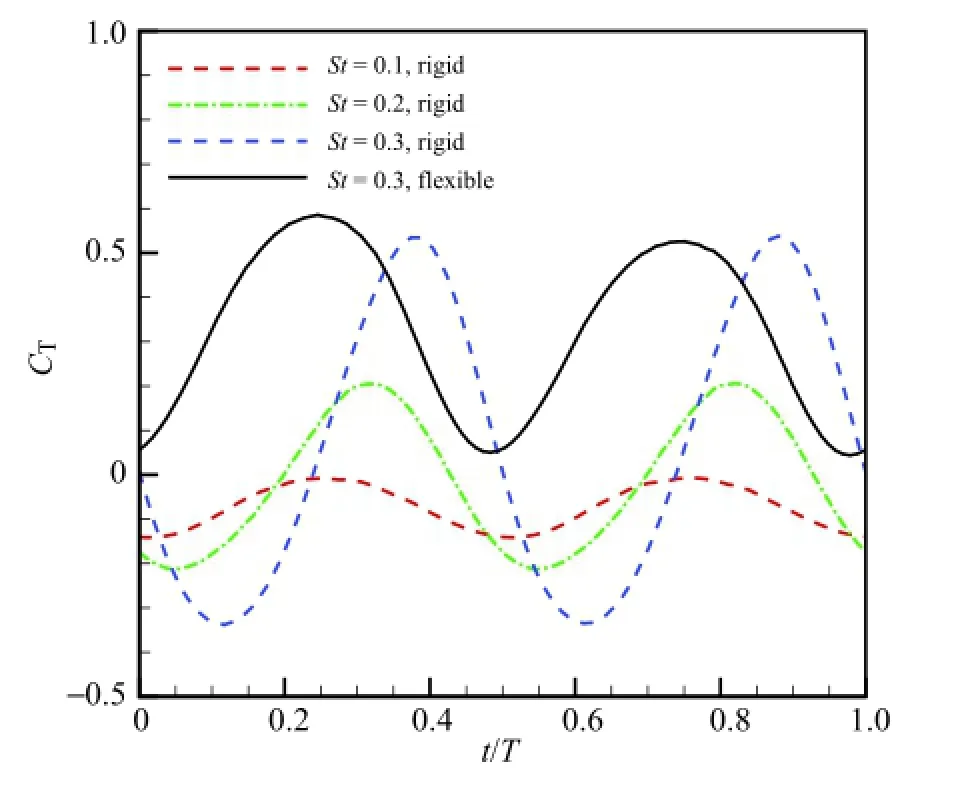
Fig.3.Evolution of thrust coefficients for rigid and flexible foils in forward flight during one flapping period at Re=1100.
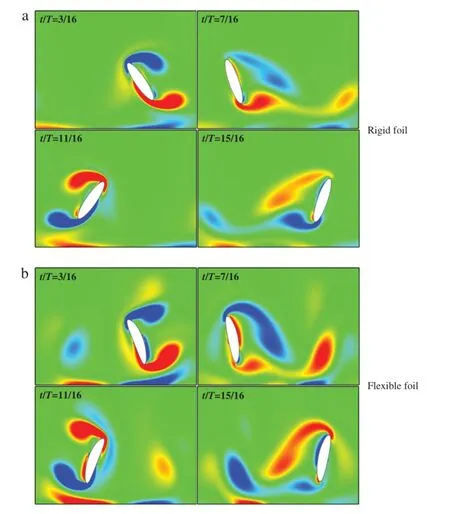
Fig.2.Instantaneous vorticity contours for the rigid foil and the flexible foil withφ=-90°.
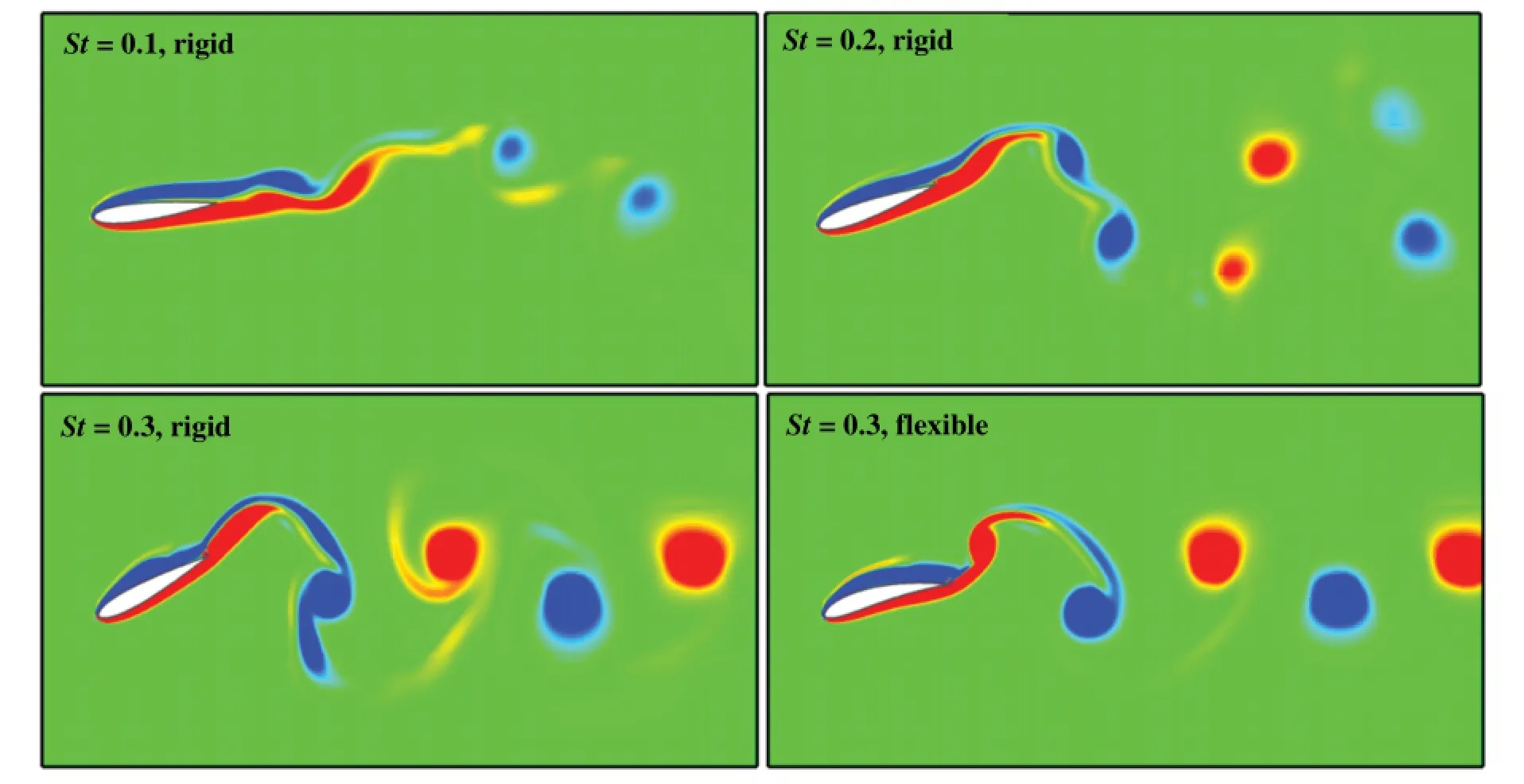
Fig.4.Instantaneous vorticity contours for the rigid and the flexible foils.
where hmandθmare respectively the plunging and pitching amplitudes,f is the frequency of oscillation.By using the free stream velocity of U∞and the double amplitude of plunge of 2hm,the Strouhal number of oscillation is defined as St=2fhm/U∞. To quantitatively determine whether the foil can generate thrust force,the nominal effective angle of attack(AoA)αncan be used[14],which is calculated by using the following relationship
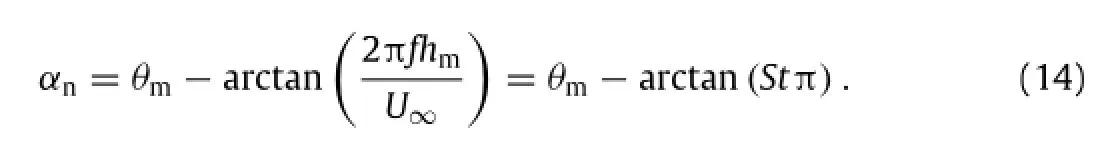
As shown by Kinsey and Dumas[6],the flapping foil is in the propulsion mode ifαn<0.In addition,the deformation of the foil is modeled by

In this study,the following parameters are used,hm=0.25c,αn=-10°,Bm=0.3c,φ=-90°and St=0.1-0.3.Moreover,the Reynolds number based on the free stream velocity and the chord length is Re=1100.The computational domain is taken by 30c×20c,and the uniform mesh spacing is h=1/160.
Figure 3 shows the evolution of thrust coefficients CTfor the rigid and flexible foils during one flapping period.At St=0.1,the flapping rigid foil cannot generate the thrust force.As St increases up to 0.2,CTpartly becomes positive and it will increase with St. Moreover,CTof the flexible foil is much larger than that of the rigid foil,which indicates that the flexibility is of importance for the locomotion of birds/insects.Figure 4 plots the instantaneous vorticity contours for the rigid and flexible foils.The clear Karman vortex street and reverse Karman vortex street can be observed at St=0.1 and St=0.3,respectively.
In this study,a coupled immersed boundary-lattice Boltzmann method for simulation of biomimetic problems is presented. Compared to the existing IB-LBM,the current method can strictly meet the no-slip boundary condition by calculating the boundary force implicitly,which is implemented through the velocity correction method.This feature is useful for handling the moving boundary problems.At the same time,the hydrodynamic force on the body can be calculated directly through the relationship between the velocity correction and forcing term.
The present IB-LBM is then employed to deal with some biomimetic problems,including a flapping wing in hovering near the ground and in forward flight.Based on the numerical results established,good agreement between the currentresults and those in the literature is observed.Therefore,it is indicated that the present IB-LBM is robust and effective for simulation of different biomimetic problems.
This work was supported by the National Natural Science Foundation of China(11272153).
[1]C.S.Peskin,Numerical analysis of blood flow in the heart,J.Comput.Phys.25(1977)220-252.
[2]C.K.Aidun,J.R.Clausen,Lattice-Boltzmann method for complex flows,Annu. Rev.Fluid Mech.42(2010)439-472.
[3]Z.G.Feng,E.E.Michaelides,The immersed boundary-lattice Boltzmann method for solving fluid-particles interaction problems,J.Comput.Phys.195(2004)602-628.
[4]Z.G.Feng,E.E.Michaelides,Proteus:a direct forcing method in the simulations of particulate flows,J.Comput.Phys.202(2005)20-51.
[5]X.D.Niu,C.Shu,Y.T.Chew,Y.Peng,A momentum exchanged-based immersed boundary-lattice Boltzmann method for simulating incompressible viscous flows,Phys.Lett.A 354(2006)173-182.
[6]J.Wu,C.Shu,Implicit velocity correction-based immersed boundarylattice Boltzmann method and its applications,J.Comput.Phys.228(2009)1963-1979.
[7]J.Hao,L.Zhu,A lattice Boltzmann based implicit immersed boundary method for fluid-structure interaction,Comput.Math.Appl.59(2010)185-193.
[8]X.Yang,X.Zhang,Z.Li,G.W.He,A smoothing technique for discrete delta functions with application to immersed boundary method in moving boundary simulations,J.Comput.Phys.228(2009)7821-7836.
[9]J.Wu,C.Shu,Numerical study of flow characteristics behind a stationary circular cylinder with a flapping plate,Phys.Fluids 23(2011)073601.
[10]J.Wu,C.Shu,Simulation ofthree-dimensionalflows overmoving objectsby an improved immersed boundary-lattice Boltzmann method,Internat.J.Numer. Methods Fluids 68(2012)977-1004.
[11]J.Wu,C.Shu,N.Zhao,Numerical investigation of vortex-induced vibration of a circular cylinder with a hinged flat plate,Phys.Fluids 26(2014)063601.
[12]T.Gao,X.Y.Lu,Insect normal hovering flight in ground effect,Phys.Fluids 20(2008)087101.
[13]W.Shyy,H.Aono,S.K.Chimakurthi,P.Trizila,C.K.Kang,C.E.S.Cesnik,H.Liu,Recentprogressin flapping wing aerodynamicsand aeroelasticity,Prog. Aerosp.Sci.46(2010)284-327.
[14]T.Kinsey,G.Dumas,Parametric study of an oscillating airfoil in a powerextraction regime,AIAA J.46(2008)1318-1330.
∗Corresponding author.
E-mail address:mpeshuc@nus.edu.sg(C.Shu).
Flapping wing near ground
Flapping wing in forward flight
*This article belongs to the Fluid Mechanics
 Theoretical & Applied Mechanics Letters2015年1期
Theoretical & Applied Mechanics Letters2015年1期
- Theoretical & Applied Mechanics Letters的其它文章
- Adjoint-based optimization of flapping plates hinged with a trailing-edge flap
- Numerical simulation of unsteady flows over a slow-flying bat
- Propulsive performance of two-and three-dimensional flapping flexible plates
- Learning from bat:Aerodynamics of actively morphing wing
- A modified criterion for wave-induced momentary liquefaction of sandy seabed
- Vortex interactions between forewing and hindwing of dragonfly in hovering flight
