Propulsive performance of two-and three-dimensional flapping flexible plates

Chao Tang，Xiyun Lu

Department of Modern Mechanics，University of Science and Technology of China，Hefei 230026，China

Propulsive performance of two-and three-dimensional flapping flexible plates

Chao Tang，Xiyun Lu∗

Department of Modern Mechanics，University of Science and Technology of China，Hefei 230026，China

A R T I C L E I N F O

Article history：

Received 21 November 2014

Received in revised form

30 December 2014

Accepted 1 January 2015

Available online 14 February 2015

Flapping-based locomotion

Self-propulsion

Flexible plate

Passive deformation

Fluid-structure interaction

The propulsive performance of two-and three-dimensional（2D and 3D）flapping flexible plates in a fluid at rest is investigated by a finite element method for the plate motion and an immersed boundary-lattice Boltzmann method for the fluid flow.We consider a model that as the leading-edge of the plate takes a vertical oscillation，the entire plate moves freely due to the fluid-structure interaction.The effects of flexibility on the dynamics of the 2D and 3D flapping plates are investigated.It is found that a suitable flexibility is benefit for improving the propulsive performance.The results obtained in this study provide physical insight into the understanding of the dynamics of the flapping-based locomotion.

©2015 The Authors.Published by Elsevier Ltd on behalf of The Chinese Society of Theoretical and Applied Mechanics.This is an open access article under the CC BY-NC-ND license（http:// creativecommons.org/licenses/by-nc-nd/4.0/）.

A common strategy of swimming or flying animals for locomotion is to use their fins or wings to make flapping motions［1-3］. The wings and fins have complex behaviors which are associated with the distribution of the compliant components［1，4］and can deform passively in response to fluid forces［5-8］.The deformations in turn affect the propulsive performances［9］.In reality the role of flexibility in the flapping-based locomotion is still completely unclear and is of great interest for future detailed studies. Moreover，the mechanical properties of wings and fins have been measured which can be used to provide a physical basis for establishing a reliable model.

For animals in free flight or swimming，the mean thrust generated balances the resistance experienced by the surrounding fluid. The dynamicalbehaviors related to the free motion should be studied.Actually，the physical models considered in extensive work are an object immersed in a given uniform incoming flow，and the relevant fluid dynamics is different from a free moving object in a stationary fluid［10］.Some efforts have been done to study the locomotion of flapping flexible bodies in a stationary fluid. The two-dimensional（2D）simulation and modeling of the lamprey swimming were performed［11］.The dynamics of a 2D heaving plate with passive pitching motion was investigated［12，13］. However，since the instantaneous shape of an elastic structure in free motion depends on the local passive deformation due to the fluid-structure interaction［9］，a modelofa three-dimensional（3D）flexible wing moving passively in a stationary fluid is needed to be considered.

The 3D effect has an important influence on the dynamic performance and vortical structures of flapping plates［14］.Recently，the 3D effects on the translational locomotion of a passive heaving wing have been investigated［15］.However，the most previous studies of the locomotion of flapping flexible plate mainly focus on the 2D model［9，16，17］.Therefore，the propulsive performances of the 2D and 3D flexible plates are desirable to be studied.

In this study，we consider a flexible plate with length c and span length R in a stationary fluid.As shown in Fig.1，the leading-edge is forced to perform a vertical oscillation

where A0is the oscillating amplitude and f the frequency.As a result of the interplay of the plate elasticity，the leading-edge forcing，and the forces exerted by the surrounding fluid，the plate starts to move freely and passively in the stationary fluid.The active pitching angle is zero in this model.The passive pitching angleαcan be defined as the angle between the x-axis and the secant connecting the leading-edge to the trailing-edge in the midspan plane.

To investigate this system of the fluid and flexible plate interaction，the incompressible Navier-Stokes equations are used to simulate the fluid flow，

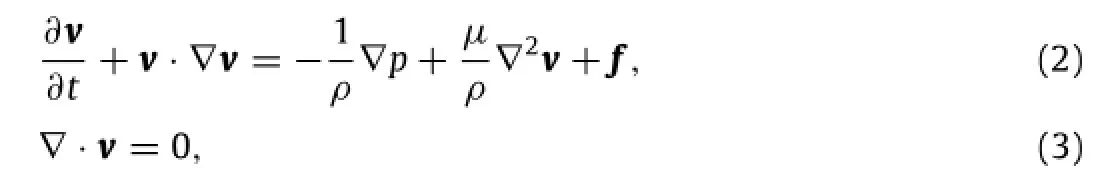
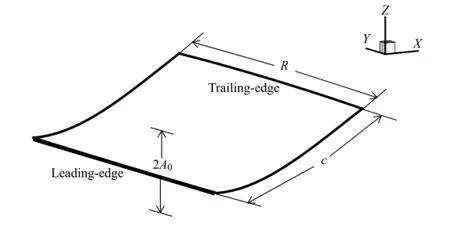
Fig.1.Schematic of the 3D flapping flexible plate.

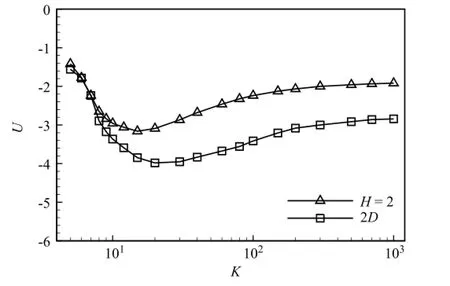
Fig.2.The mean propulsive speed U versus the bending stiffness K.

where v is the velocity，p the pressure，ρthe density of the fluid，µthe dynamic viscosity，and f the body force term.The structural equation is used to describe the plate deformation and motion［18］

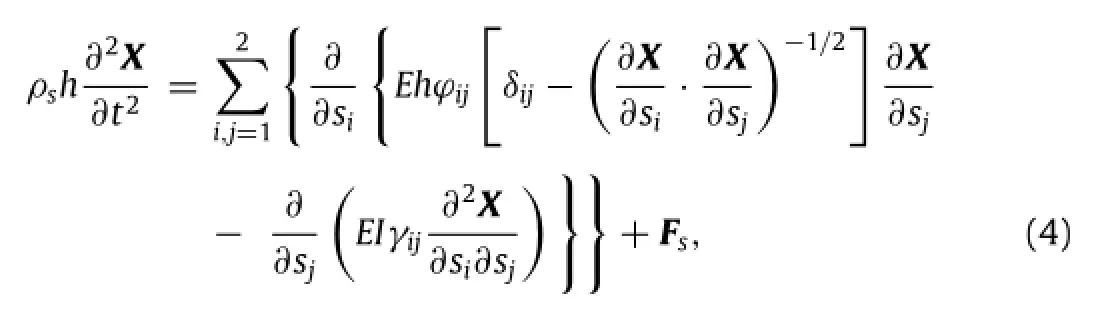
where X isthe position vectorofthe plate，Fsisthe Lagrangian force exerted on the plate by the fluid，Eh and EI are the stretching and bending stiffness of the plate，ϕijandγijare the in-plane and outof-plane effect matrices，respectively，andδijis the Kronecker delta function.

The characteristic quantitiesρ，f，and c are chosen to nondimensionalize the above equations.Then the governing parameters are obtained as follows:the heaving amplitude A=A0/c，the frequency Reynolds number Ref=ρfc2/µ，the aspect ratio H=R/c，the stretching stiffness S=Eh/（ρf2c3），the bending stiffness K=EI/（ρf2c5），and the mass ratio of the plate and the fluid M=ρsh/（ρc）.

The governing equations of the fluid-plate problem are solved numerically.When the immersed boundary（IB）method is applied to analyze flow-structure interaction，the body force term f in Eq.（2）is used as an interaction force between the boundary and the fluid to enforce the no-slip velocity boundary condition on the surface.The lattice Boltzmann equation with the body force model and non-uniform mesh technique are employed to solve the viscous fluid flow.Equation（4）for the deformable plate is solved by a finite element method and the deformation with large-displacement of the plate is handled by the corotational scheme［19］.

After our careful convergence studies，the computational domain for fluid flow is chosen as［-5，15］×［-6，6］×［-6，6］in the x，y，and z directions.The finest lattice spacing is 0.025 in the nearplate region and the coarsestspacing is 0.1 in the farboundary region.The plate is discretized by approximate 8000 triangular elements.The time step isΔt=0.0005.

Based on a series ofsimulations，we have identifiedsome typical movement states of the plate due to the fluid-plate interaction. The plate motion along the negative x-direction is mainly analyzed since the motion is related to the flapping-based locomotion of swimming and flying animals.In this study，some typical results are discussed for the parameters A=0.5，Ref=100，H=2， K=5-1000，S=1000 and M=2.The dynamical behavior and propulsive performance are analyzed in terms of the mean propulsive speed，the propulsive efficiency，the passive pitching angle，and the Strouhal number.

We first analyze the behavior of the propulsive speed of the plate.Figure 2 shows the mean propulsive speed U versus the bending rigidity K for the 2D and 3D plates，where U is obtained by time average during steady locomotion.It is seen that the profiles of U are all concave up.The speed U decreases as K increases first，then reaches a minimum（corresponding to the maximum of |U|），and finally approaches a constant as K increases further.The forward speed|U|for the 2D plate is overall larger than that for the 3D plate.Note that the motion of the flexible plate tends to the motion of the rigid one at large value of K，e.g.K=1000.The forward speeds of the flexible plate are substantially greater than those ofthe corresponding rigid plate，indicating that the flexibility can improve the performance of forward propulsion.

The propulsive efficiency is investigated for the plate motion.As the plate spontaneously propels itself in the horizontal direction，the mean thrust becomes zero.To characterize the propulsive efficiency of a body in free motion，the ratio of the kinetic energy of the body motion and the work done by the deforming body over one flapping cycle T has been employed［9，13］.Then，the propulsive efficiency for the locomotion of flexible plate is expressed as

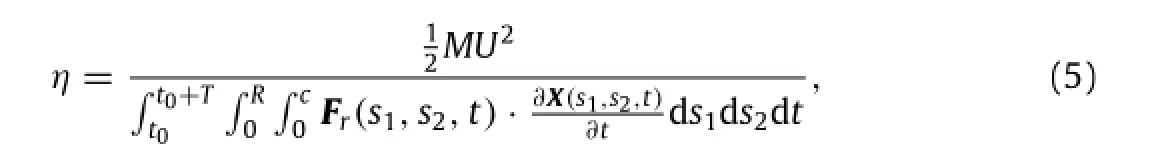
where Fr（s1，s2，t）represents the force on the surrounding fluid by the plate and can be expressed as Fr（s1，s2，t）=-Fs（s1，s2，t）. As shown in Fig.3 for the propulsive efficiencyη，the efficiency first increases to a maximum and then decreases gradually as K increases for both the 2D and 3D plates.It is also identified that the efficiencyηfor the 2D plate is larger than that for the 3D plate. Similarly，there exists an optimal plate flexibility region for the maximal propulsive efficiency.

The passive pitching angle is associated with the deformation of the flexible plate and with hydrodynamic performance［3，20］. Figure 4 shows the root-mean-square（rms）value of the passive pitching angleαrmsfor the 2D and 3D plates.The passive pitching angle is caused by the delayed motion of the free end of the plate relative to the constrained end.It is seen from Fig.4 that smaller bending stiffness or more flexibility causes larger pitching angle. Comparing the profiles ofαrms，the pitching angles of the 3D plate are somewhat larger than those of the 2D plate for K＜100，and the pitching angles of the 2D and 3D plates tend to be together for K＞100.

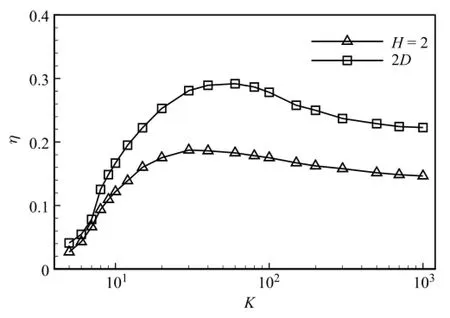
Fig.3.The propulsive efficiencyηversus the bending stiffness K.

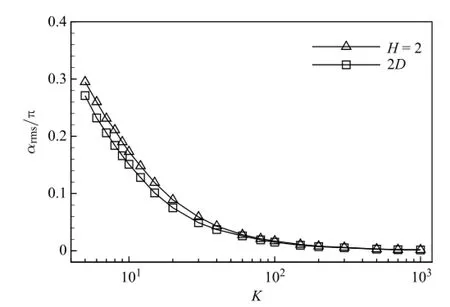
Fig.4.The rms value of passive pitching angleαrmsversus the bending stiffness K.

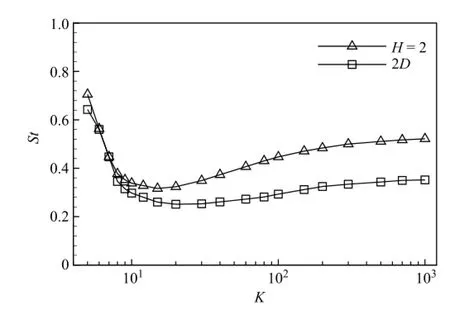
Fig.5.The Strouhal number St versus the bending stiffness K.

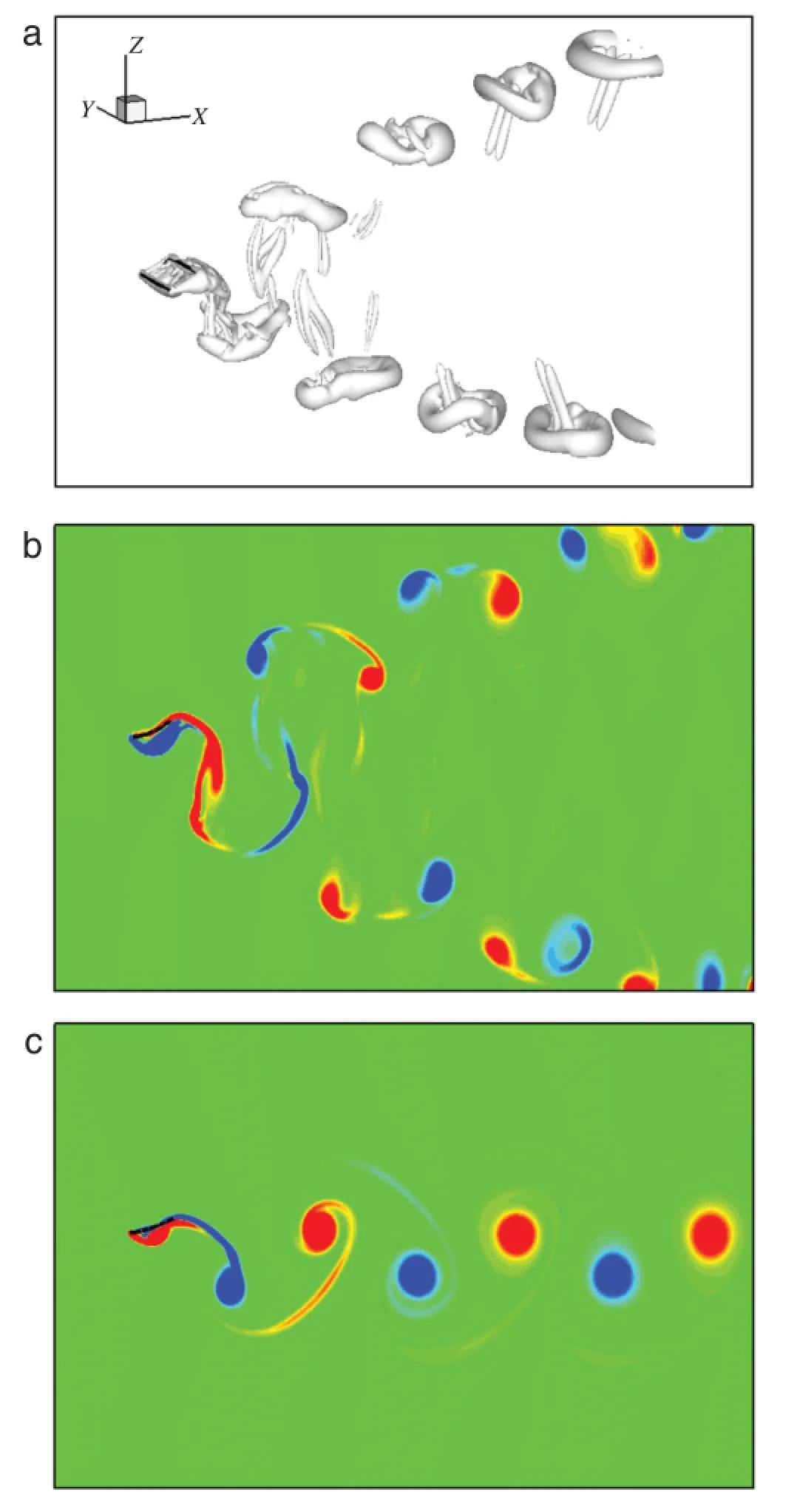
Fig.6.Vortical structures for K=15:（a）vortical pattern visualized by isosurface of Q=3 for 3D plate，（b）spanwise vorticity contour on the spanwise symmetry plane for 3D plate，and（c）vorticity contour for 2D plate.

The Strouhal number is usually used to describe the kinematics of flapping-based locomotion and a well-defined series of regimes for vortex growth and shedding of a flapping body.Here the Strouhal number is defined as St=Awf/U，where Awis the width of the wake which may be taken as the maximum excursion of the plate trailing-edge or twice of the amplitude，i.e.Aw=2A［9，21］. Figure 5 shows the profiles of the Strouhal number.The Strouhal numbers for K=O（10）-O（102）fall into the range of St=0.2-0.4 which is consistent with the region of high propulsive efficiency of the flapping-based locomotion［3，22］.Moreover，according to experimental data for some swimming and flying animals［23-26］，we can estimate the bending stiffness of tail-fins or wings to be the range of K=O（10）-O（102），which also corresponds to the large forward speed in Fig.2 and high propulsive efficiency in Fig.3.

We finally investigate the vortical structures around the 2D and 3D plates.The vortical structure in the wake is related to the propulsive properties of a flapping wing.Based on the analysis of vorticity dynamics，we have found that the force and power of the flapping plate are dominated by the attached vorticity and the localvorticalstructures close to the plate［27，28］.Figure 6（a）shows the 3D perspective view of vortical structures depicted by an isosurface of the Q criterion for K=15.It is seen that the wake consists of two sets of ring-like vortical structures which convect downstream separately.This feature is essentially consistent withthe previous observation［14，28］.Figures 6（b）and 6（c）shows the spanwise vorticity contour on the spanwise symmetry plane for the 3D plate and the vorticity contour for the 2D plate.The wake of the 3D plate demonstrates two branches of vorticity contours relevant to the ring-like structures.For comparison，a reverse von Kármán vortex street is formed behind the 2D flexible plate［9］. Further，to demonstrate the effect of K on the vortical structures，Fig.7 shows the vortex patterns for K=8.In the 3D case，the vortical structures in the wake are still nearly anti-symmetric and become more complex compared with the case for K=15 in Fig.6. It is interesting to note that the deflected wake occurs for the 2D case in Fig.7（c），resulting in a non-zero mean lift［9］.

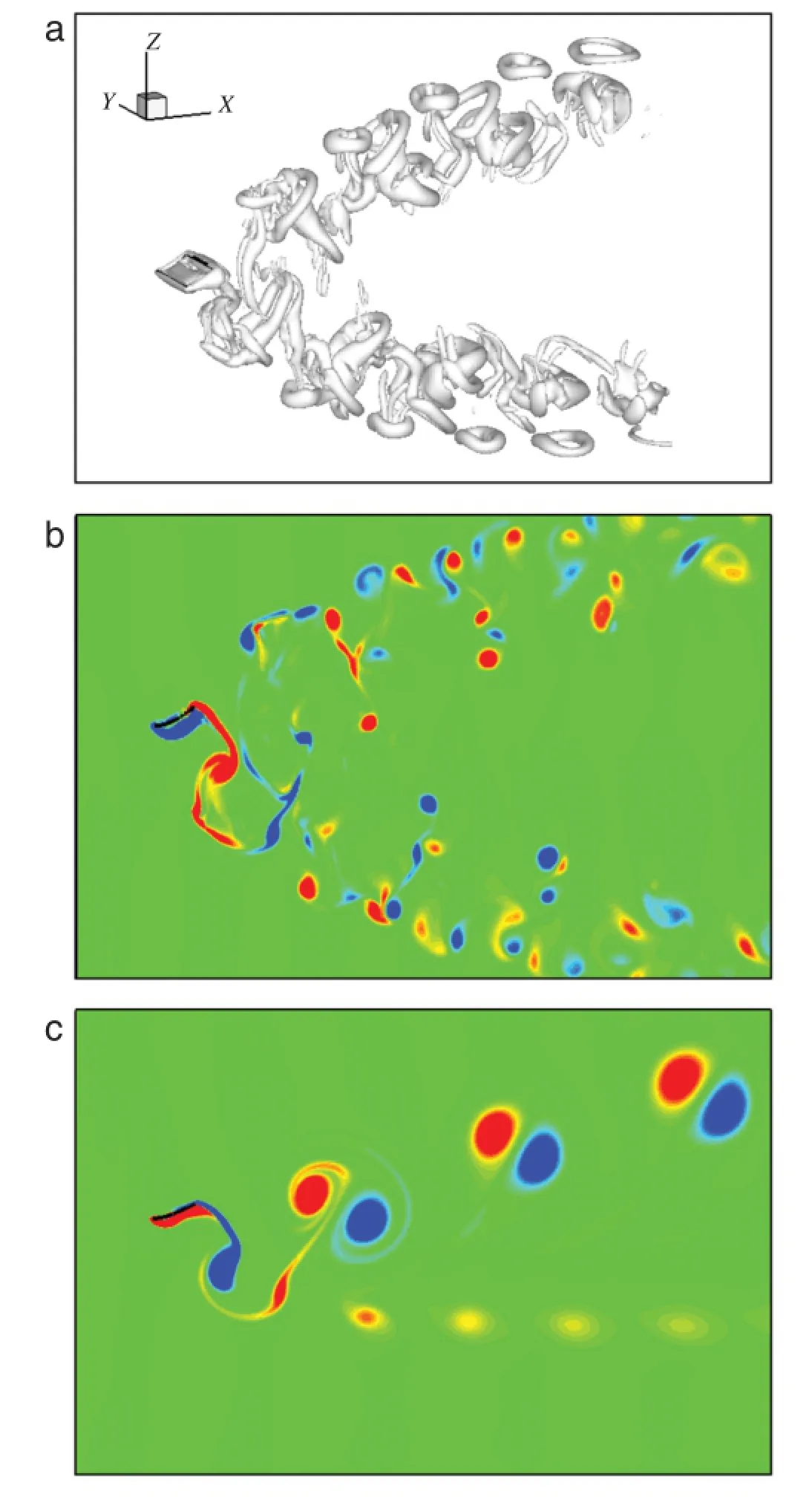
Fig.7.Vortical structures for K=8:（a）vortical pattern visualized by isosurface of Q=3 for 3D plate，（b）spanwise vorticity contour on the spanwise symmetry plane for 3D plate，and（c）vorticity contour for 2D plate.

In summary，the propulsive performance of flapping flexible plates in a stationary fluid has been studied by numerical solutions of the fluid and plate interaction.Some mechanisms governing the dynamics of the flapping plates are investigated.It is found that a suitable degree of flexibility can improve the propulsive performance with larger forward speed and higher propulsive efficiency for the 2D and 3D plates.Smaller bending stiffness causes larger passive pitching angle.The vortical structure around the plate is analyzed because itaffects the motion and deformation of the plate.Further，the range of high propulsive efficiency corresponds to the Strouhal number St=0.2-0.4 and the bending stiffness K=O（10）-O（102）which are usually adopted by the swimming and flying animals.

Acknowledgments

This work was supported by the National Natural Science Foundation of China（11372304）and the 111 Project（B07033）.

［1］J.J.Videler，Fish Swimming，Chapman&Hall，New York，1993.

［2］A.K.Brodsky，The Evolution of Insect Flight，Oxford University Press，Oxford，1994.

［3］M.S.Triantafyllou，G.S.Triantafyllou，D.K.P.Yue，Hydrodynamics of fishlike swimming，Annu.Rev.Fluid Mech.32（2000）33-53.

［4］R.J.Wootton，Invertebrate paraxial locomotory appendages:design，deformation and control，J.Exp.Biol.202（1999）3333-3345.

［5］R.J.Wootton，R.C.Herbert，P.G.Young，K.E.Evans，Approaches to structural modeling of insect wings，Phil.Trans.R.Soc.Lond.B 358（2003）1577-1587.

［6］S.A.Combes，T.L.Daniel，Flexural stiffness in insect wings.I.Scaling and the influence of wing venation，J.Exp.Biol.206（2003）2979-2987.

［7］S.A.Combes，T.L.Daniel，Flexural stiffness in insect wings.II.Spatial distribution and dynamic wing bending，J.Exp.Biol.206（2003）2989-2997.

［8］F.Fish，G.Lauder，Passive and active flow control by swimming fishes and mammals，Annu.Rev.Fluid Mech.38（2006）193-224.

［9］R.N.Hua，L.Zhu，X.Y.Lu，Locomotion of a flapping flexible plate，Phys.Fluids 25（2013）121901.

［10］T.Y.T.Wu，On theoretical modeling of aquatic and aerial animal locomotion，Adv.Appl.Mech.38（2001）291-353.

［11］E.D.Tytell，C.Y.Hsu，T.L.Williams，A.H.Cohen，L.J.Fauci，Interactions between internal forces，body stiffness，and fluid environment in a neuromechanical model of lamprey swimming，Proc.Natl.Acad.Sci.107（2010）19832.

［12］S.E.Spagnolie，L.Moret，M.J.Shelley，J.Zhang，Surprising behaviors in flapping locomotion with passive pitching，Phys.Fluids 22（2010）041903.

［13］J.Zhang，N.S.Liu，X.Y.Lu，Locomotion of a passively flapping flat plate，J.Fluid Mech.659（2010）43-68.

［14］J.H.Buchholz，A.J.Smits，The wake structure and thrust performance of a rigid low-aspect-ratio pitching panel，J.Fluid Mech.603（2008）331-365.

［15］J.Hu，Q.Xiao，Three-dimensional effects on the translational locomotion of a passive heaving wing，J.Fluids Struct.46（2014）77-88.

［16］J.Lee，S.Lee，Fluid-structure interaction forthe propulsive velocity ofa flapping flexible plate at low Reynolds number，Comput.Fluids 71（2013）348-374.

［17］X.J.Zhu，G.W.He，X.Zhang，Numerical study on hydrodynamic effect of flexibility in a self-propelled plunging foil，Comput.Fluids 97（2014）1-20.

［18］W.X.Huang，H.J.Sung，Three-dimensional simulation of a flapping flag in a uniform flow，J.Fluid Mech.653（2010）301-336.

［19］J.F.Doyle，Nonlinear Analysis of Thin-Walled Structures:Statics，Dynamics，and Stability，Springer-Verlag，2001.

［20］J.M.Anderson，K.Streitlien，D.S.Barrett，M.S.Triantafyllou，Oscillating foils of high propulsive efficiency，J.Fluid Mech.360（1998）41-72.

［21］M.S.Triantafyllou，G.S.Triantafyllou，R.Gopalkrishnan，Wake mechanics for thrust generation in oscillating foils，Phys.Fluids 3（1991）2835-2837.

［22］G.K.Taylor，R.L.Nudds，A.L.R.Thomas，Flying and swimming animals cruise ata Strouhalnumbertuned forhigh power efficiency，Nature 425（2003）707-711.

［23］S.A.Wainwright，W.D.Biggs，J.D.Currey，J.M.Gosline，Mechanical Design in Organisms，Princeton University Press，Princeton，1982.

［24］C.P.Ellington，The aerodynamics of hovering insect flight.II.Morphological parameters，Phil.Trans.R.Soc.Lond.B 305（1984）17-40.

［25］D.Ishihara，T.Horie，M.Denda，Atwo-dimensionalcomputationalstudy on the fluid-structure interaction cause of wing pitch changes in dipteran flapping flight，J.Exp.Biol.212（2009）1-10.

［26］S.R.Jongerius，D.Lentink，Structural analysis of a dragonfly wing，Exp.Mech. 50（2010）1323-1334.

［27］J.Z.Wu，X.Y.Lu，L.X.Zhuang，Integral force acting on a body due to local flow structures，J.Fluid Mech.576（2007）265-286.

［28］G.J.Li，X.Y.Lu，Force and power of flapping plates in a fluid，J.Fluid Mech.712（2012）598-613.

∗Corresponding author.

E-mail address：xlu@ustc.edu.cn（X.Lu）.

*This article belongs to the Fluid Mechanics