A modified criterion for wave-induced momentary liquefaction of sandy seabed

Wen-Gang Qi，Fu-Ping Gao

Key Laboratory for Mechanics in Fluid Solid Coupling Systems，Institute of Mechanics，Chinese Academy of Sciences，Beijing 100190，China

A modified criterion for wave-induced momentary liquefaction of sandy seabed

Wen-Gang Qi，Fu-Ping Gao∗

Key Laboratory for Mechanics in Fluid Solid Coupling Systems，Institute of Mechanics，Chinese Academy of Sciences，Beijing 100190，China

A R T I C L E I N F O

Article history：

Received 23 October 2014

Accepted 29 October 2014

Available online 14 February 2015

Pore-pressure response

Liquefaction criterion

Momentary liquefaction

Analytical approximation

The assessment of the wave-induced soil liquefaction plays a key role in the geotechnical design for offshore foundations.The underlying shortcomings of the existing momentary liquefaction criteria are identified and clarified by mechanism analyses and the recent field observations.A modified criterion for the wave-induced momentary liquefaction of a sandy seabed is given to describe the vertical porepressure distributions.An improved approximation of the momentary liquefaction depth is further presented.Parametric study of the effects of the saturation degree of soils indicates that this modification is significant for the evaluation of wave-induced momentary liquefaction.

©2015 The Authors.Published by Elsevier Ltd on behalf of The Chinese Society of Theoretical and Applied Mechanics.This is an open access article under the CC BY license（http://creativecommons.org/ licenses/by/4.0/）.

Liquefaction is the act or process of transforming any substance into a liquid.In the offshore environments，soil liquefaction may occur and the soil particles would become unbound.The resulting loss of the soil strength could produce catastrophic consequences，such as sinking and floatation of pipelines，failure of breakwater，and instability of offshore foundations.Thus in offshore engineering practices，the occurrence of soil liquefaction and its effect on the structures should be well assessed.

Based on the observations in laboratory experiments and field measurements，two mechanisms for wave-induced pore-pressure response have been identified［1］，which are oscillatory porepressure and residual pore-pressure.Soil liquefaction can be generated by either the oscillatory or residual pore-pressure with differentmechanisms.Oscillatory pore-pressure is found to propagate into seabed with certain damping and phase lag.At the wavetrough phase，wave-induced pore-pressure exerts an upward seepage force onto the particles and can momentarily liquefy the sandy soils if the seepage force is larger than the submerged weightofthe soilparticle［2，3］.Residualpore-pressure refers to the build-up of excess pore-pressure caused by contraction of the soil under the action of cyclic wave loading similar to the earthquakeinduced pore-pressure accumulation.Under the continuous action of the cyclic wave loading，the excessive pore-pressure may build up gradually and the soil is liquefied when the residual porepressure exceeds the effective overburden pressure.

Much attention has been devoted to calculating the porepressure response and deducing the liquefaction depth，mostly based on Biot's theory for poro-elastic media［4］.Some approximations for the prediction of wave-induced liquefaction potential have been previously proposed for engineering practice［2，5，6］.However，some underlying shortcomings of the momentary liquefaction criteria still remain，which could generate unreasonable results in assessing the momentary liquefaction depth.In this study，the pore-pressure based liquefaction criteria are discussed and some underlying shortcomings are clarified.A modified momentary liquefaction criterion is proposed and pore-pressure distribution is calculated correspondingly，which provides a simple approximation of momentary liquefaction depth.

An appropriate liquefaction criterion is crucial to evaluation of the liquefaction depth of soils under the wave loading.The criterion commonly adopted for residual liquefaction is［7］pres=σ′v0，where presrepresents the residual pore-pressure andσ′v0denotes the initialverticaleffective stress，which can be calculated byσ′v0= γ′z.Hereγ′is the submerged unit weight of the soil and z is the soil depth.This criteria for residual liquefaction can be easily comprehended by viewing the balance of forces acting on the liquefied soil layer during the event.

Regarding momentary liquefaction，Jeng［8］summarized three kinds of pore-pressure-based criteria.It is concluded that the liquefaction criteria based on the concept of effective stress［9，10］would not be applicable due to inaccuracies in determining the effective stress at shallow soil depth.A liquefaction criterion was ever suggested by Zen and Yamazaki［11］for the two-dimensional（2-D）case:

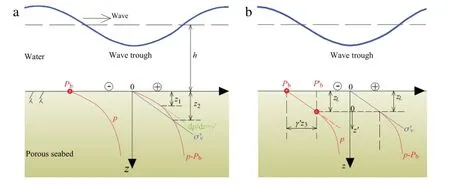
Fig.1.Distribution of pore-pressure response and definitions of momentary liquefaction depths:（a）employing Eqs.（1）and（2）；（b）employing Eqs.（3）and（12）（z1:liquefaction depth calculated with Eq.（2），z2:liquefaction depth calculated with Eq.（1），zL:liquefaction depth considering the redistribution of pore-pressure in the liquefied soil）.

where Pbis the wave pressure atthe seabed surface（negative value at wave trough phase），p is the wave-induced oscillatory porepressure in the soil.

The physical nature of the momentary liquefaction is the vanishing of the contact between the soil particles due to the seepage force resulting from the pore-pressure gradient along the soil depth.When the soilis liquefied，the verticalseepage force exceeds the submerged weight of the soil particles［12］.Accordingly，another criterion for momentary liquefaction was proposed by Xu et al.［13］as:

where jz=d p/d z（pore-pressure vertical gradient）is the seepage force acting on the soil skeleton.

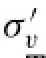
When the liquefaction criterion expressed with Eq.（1）is adopted，the soilparticles located fromdepth z1to z2are practically in a partially-suspended state but not fully liquefied because Eq.（2）is not satisfied（see Fig.1（a））.Thus，the liquefaction depth determined with Eq.（1）is inaccurate.If the liquefaction criterion expressed with Eq.（2）is employed，the soil particles located from depth 0 to z1will be in an over-suspension state，and a resultant upward movement would be expected because a vertical net force would be exerted（γ′≤jz，see Fig.1（a））.Nevertheless，once the soilhave been liquefied，it willbehave like a fluid and thus no more excess pressure gradient can be sustained in it except the essential one（seepage force）for maintaining the soil liquefied.Thus the over-suspension state of the soil particles located from depth 0 to z1is unlikely to occur.

In a field study of momentary liquefaction，Mory et al.［3］observed that the pressure difference between two pore-pressure sensors located at the mudline（z=0）and the depth of z=0.3 m below mudline did not typically exceed the critical value for liquefaction to occur（breaking the static equilibrium of the sediment layer contained between two sensors）during allthe recorded momentary liquefaction events.The explanation provided is that when momentary liquefaction occurs liquefaction produces a dilated suspension and the pore-pressure is rapidly adjusted to the value on top of the soil.This observation provides some evidence for the conclusion that the over-suspended state of the soil particles in the liquefied layer is not likely.

According to the aforementioned discussion and the field observation of pore-pressure distribution in the liquefied layer，it can be reasonably assumed that the soil particles in the liquefied layer should be in an exact suspended state（neither over-suspended nor partially-suspended）.Thus following conditions should be satisfied at any position in the momentary liquefaction soil layer

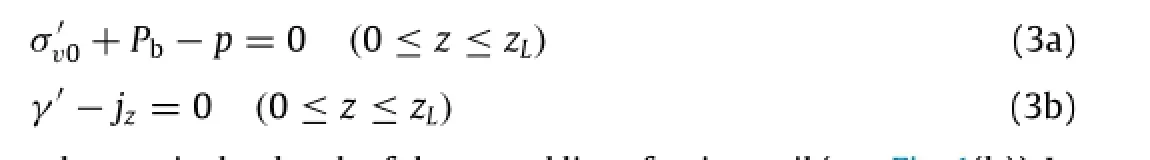
where zLis the depth ofthe actualliquefaction soil（see Fig.1（b））.In fact，Eqs.（3a）and（3b）are equivalent，and Eq.（3a）can be derived by directly integrating Eq.（3b）from 0 to zL.Under this assumption，the liquefied soil acts like a heavy liquid and there is no extra pressure gradient in this liquid.

Below the liquefied soil layer，the pore-pressure distribution can be described on the basis of poroelastic solutions［14］.It was pointed out by Zen and Yamazaki［15］that for the case of relatively long waves wave-seabed interaction can be analyzed with a onedimensional（1-D）approach because，under the action of long period waves，the flow and deformation in the horizontal direction are typically negligible because the steepness of the wave is relatively low.Chowdhury et al.［16］also showed that the 1-D solution of pore-pressure can reasonably be used for the purpose of momentary liquefaction analysis of the seabed under waves，particularly under shallow water wave condition.For 1-D analysis of wave-induced seabed response，Chowdhury［17］presented the following governing differentialequationsby assuming pore fluid and soil mass both to be compressible and adopting Darcy's law

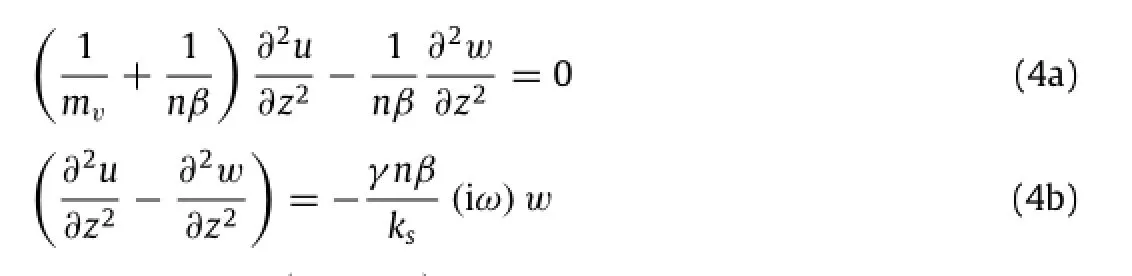
Corresponding boundary conditions are adopted as follows at z=0:

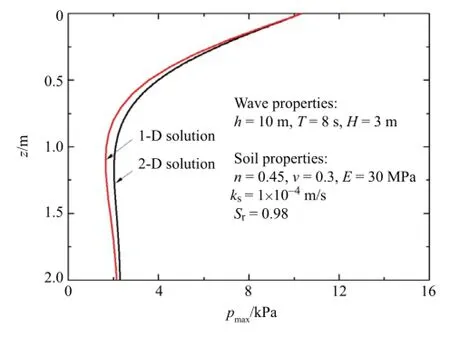
Fig.2.Comparison of 1-D and 2-D solutions of maximum pore-pressure response under waves.

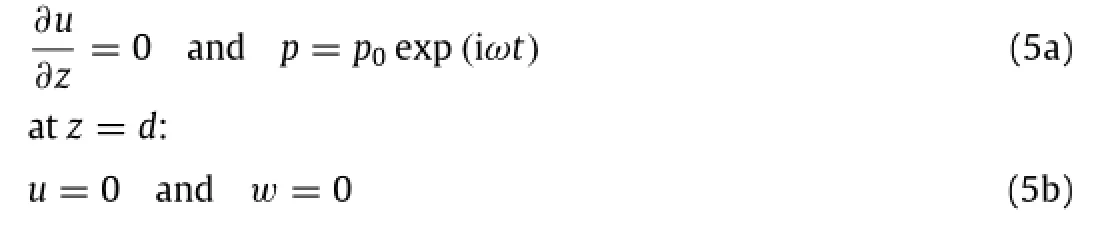
A simple closed form solution of pore-pressure under the 1-D approximation developed by Chowdhury［17］，according to Eqs.（4）-（5），is:

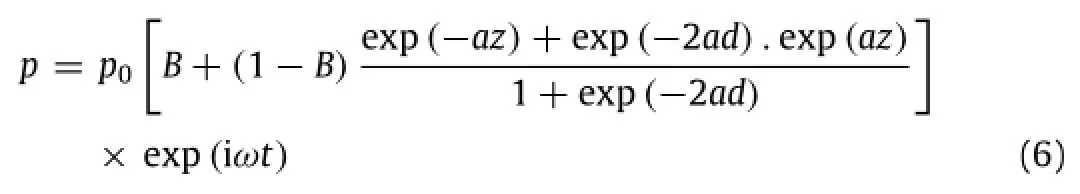
Figure 2 shows the comparison of analytical results from 1-D（Eq.（8））to 2-D［14］solutions for a typical wave-seabed interaction problem.Itis shown that the pore-pressure distributions using 1-D and 2-Danalyses are reasonably close to eachother near the seabed surface，although there exists slight divergence with depth.

The momentary liquefaction depth can be estimated according to the aforementioned assumed pore-pressure gradient distribution in the liquefied layer represented by Eq.（3b）and the porepressure distribution below the liquefied layer represented by following expression（see Fig.1（b））

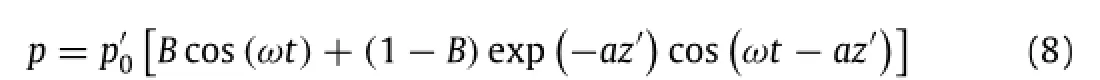
where p′0=p0-γ′zL，and z′=z-zL.At z=zL（z′=0，interface of the liquefied and un-liquefied soil layers），the following condition must be satisfied

The left term of Eq.（9）can be obtained from Eq.（8）by

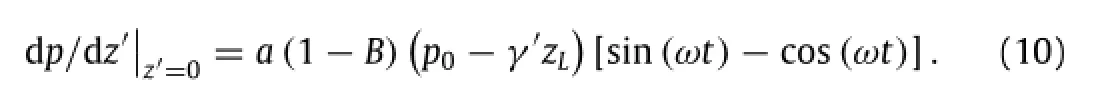
Substituting Eq.（10）into Eq.（9），the liquefaction depth zLcan be written as

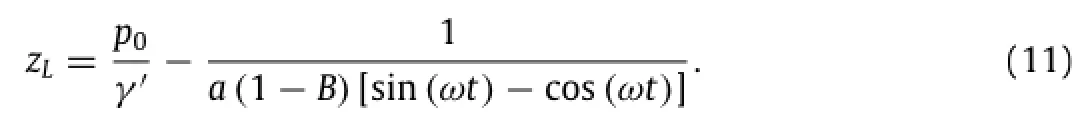
Under the wave trough phase，puttingωt=πinto Eq.（11），the maximum momentary liquefaction depth can be expressed as

The saturation degree of the soil may have effect on the porepressure distribution and the resultant momentary liquefaction depth.The large pressure gradient in the case of unsaturated soil is caused by the air/gas content of the soil.Only a very small amount of gas（less than 1%）can cause very large dissipation of the pore-pressure over the depth and thus resulting in an increased likelihood of liquefaction［9］.Previous studies suggested that an air content of up to 3%-5%may typically be present in the pores of many seabeds［18］，implying a somewhat higher potential for momentary liquefaction than the idealized case of a saturated seabed.

The variations of the maximum momentary liquefaction depth with Sradopting original pore-pressure distribution and corresponding criteria（Eqs.（1），（2），and（7）），and the improved approximation（Eq.（12）），are shown in Fig.4 for a typical set of the other soil parameters and wave conditions.The results show relatively large differences.The momentary liquefaction depth adopting the improved approximation generally locates in between of those from the criteria expressed with Eqs.（1）and（2）.A significant decrease of momentary liquefaction depth is indicated with the increase of Srfor the range of 0.98＜Sr＜0.993.For the condition of Sr＜0.98，the values of the liquefaction tend to be stable. For a nearly saturated soil，momentary liquefaction rarely occurs.

Momentary liquefaction usually occurs in the upper layer of the sandy seabed.The maximum momentary liquefaction depth generally does not exceed half of the wave height［2］.Therefore，it usually has much influence on the shallowly embedded structures（e.g.submarine pipelines）.In the on-bottom stability design of submarine pipelines，an appropriate estimation of liquefaction susceptibility is crucial to determining the required burial depth to avoid the sinking/floatation of pipelines［16，19］.The present updated approximation of momentary liquefaction depth may provide a more reasonable evaluation for the stability of such submarine structures.

Acknowledgment

This work was supported by the National Natural Science Foundation of China（11232012 and 10872198）and the Major State Basic Research Development Programof China（973 Program）（2014CB046204）.

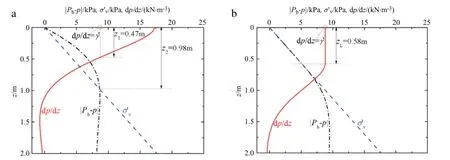
Fig.3.Vertical distributions of|Pb-p|，σ′v0and d p/d z:（a）using Eq.（7）；（b）using Eqs.（8）and（12）.（Wave parameters:h=10 m，T=8 s，H=3 m；soil properties: ks=1×10-4m/s，E=30 MPa，γ′=8.82 kN/m3，Sr=0.98，n=0.45，ν=0.3.）

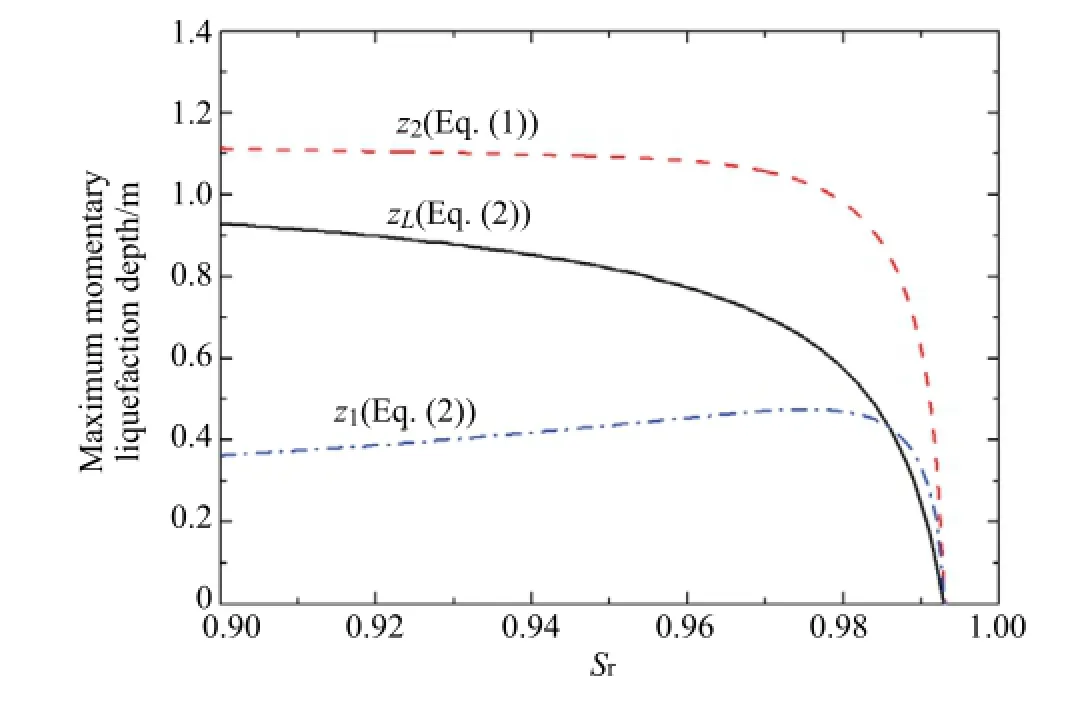
Fig.4.Comparison of the variations of the maximum momentary liquefaction depth with Sremploying different liquefaction criteria.（Wave parameters:h= 10 m，T=8 s，H=3 m；soil properties:ks=1×10-4m/s，E=30 MPa，γ′=8.82 kN/m3，n=0.45，ν=0.3.）

［1］H.Nago，S.Maeno，T.Matsumoto，et al.Liquefaction and densification of loosely deposited sand bed under water pressure variation，in:The Third international offshore and polar engineering conference.Singapore，1993，pp.6-11.

［2］T.Sakai，K.Hatanaka，H.Mase，Wave-induced effective stress in seabed and its momentary liquefaction，J.Waterway Port Coastal Ocean Eng.118（1992）202-206.

［3］M.Mory，H.Michallet，D.Bonjean，et al.，A field study of momentary liquefaction caused by waves around a coastal structure，J.Waterway Port Coastal Ocean Eng.133（2007）28-38.

［4］D.S.Jeng，Wave-induced sea floor dynamics，Appl.Mech.Rev.56（2003）407-429.

［5］D.S.Jeng，B.Seymour，F.P.Gao，et al.，Ocean waves propagating over a porous seabed:Residual and oscillatory mechanisms，Sci.China Ser.E Technol.Sci.50（2007）81-89.

［6］Z.Guo，D.S.Jeng，W.Guo，Simplified approximation of wave-Induced liquefaction in a shallow porous seabed，Int.J.Geomech.（2013）.

［7］S.Sassa，H.Sekiguchi，J.Miyamoto，Analysis of progressive liquefaction as a moving-boundary problem，Geotechnique 51（2001）847-857.

［8］D.S.Jeng，Wave-induced seabed instability in frontofa breakwater，Ocean Eng. 24（1997）887-917.

［9］S.Okusa，Wave-induced stress in unsaturated submarine sediments，Geotechnique 35（1985）517-532.

［10］C.P.Tsai，Wave-induced liquefaction potential in a porous seabed in front of a breakwater，Ocean Eng.22（1995）1-18.

［11］K.Zen，H.Yamazaki，Mechanism of wave-induced liquefaction and densification in seabed，Soil Found.30（1990）90-104.

［12］J.Bear，Dynamics of Fluids in Porous Media，Courier Dover Publications，Dove，1972.

［13］Y.F.Xu，J.H.Wang，J.J.Chen，Cnoidal water wave induced seepage in a permeable seabed with a defined thickness，Coast.Eng.80（2013）95-99.

［14］T.Yamamoto，H.L.Koning，H.Sellmeijer，etal.，On the response ofa poro-elastic bed to water waves，J.Fluid Mech.87（1978）193-206.

［15］K.Zen，H.Yamazaki，Wave-induced liquefaction in a permeable seabed，Rep. Port Harbours Res.Inst.31（1993）155-192.

［16］B.Chowdhury，G.R.Dasari，T.Nogami，Laboratory study of liquefaction due to wave-seabed interaction，J.Geotech.Geoenviron.Eng.132（8）（2006）842-851.

［17］B.Chowdhury，One-dimensional study of wave-induced momentary liquefaction of the seabed（MEng thesis），National University of Singapore，Singapore，2003.

［18］Tørum，Wave-induced pore pressures—air/gas content，J.Waterway Port Coastal Ocean Eng.133（2007）83-86.

［19］M.Sumer，J.Fredsøe，S.Christensen，et al.，Sinking/floatation of pipelines and other objects in liquefied soil under waves，Coast.Eng.38（1999）53-90.

∗Corresponding author.

E-mail addresses：qwg1989@foxmail.com（W.-G.Qi），fpgao@imech.ac.cn（F.-P.Gao）.

*This article belongs to the Solid Mechanics