Numerical simulation of unsteady flows over a slow-flying bat

Shizho Wng，Xing Zhng，Guowei He，∗，Tinshu Liub，

aThe State Key Laboratory of Nonlinear Mechanics，Institute of Mechanics，Chinese Academy of Sciences，Beijing 100190，China

bDepartment of Mechanical and Aerospace Engineering，Western Michigan University，Kalamazoo，MI 49008，USA

Numerical simulation of unsteady flows over a slow-flying bat

Shizhao Wanga，Xing Zhanga，Guowei Hea，∗，Tianshu Liub，a

aThe State Key Laboratory of Nonlinear Mechanics，Institute of Mechanics，Chinese Academy of Sciences，Beijing 100190，China

bDepartment of Mechanical and Aerospace Engineering，Western Michigan University，Kalamazoo，MI 49008，USA

A R T I C L E I N F O

Article history：

Received 21 November 2014

Accepted 27 December 2014

Available online 14 February 2015

Flapping flight

Bat

Lift

Leading-edge vortex

Vortex lift

Numerical simulation

This letter describes numerical simulation of the unsteady flow over a slow-flying bat by using the immersed boundary method based on the measured batwing geometry and kinematics.The main vortical structures around the batflapping wings are identified，illuminating the lift-generating role ofthe leadingedge vortices generated mainly in the downstroke.Furthermore，the lift decomposition indicates that the vortex lift has the dominant contribution to the time-averaged lift and the lift associated with the fluid acceleration has the relatively moderate effect.

©2015 The Authors.Published by Elsevier Ltd on behalf of The Chinese Society of Theoretical and Applied Mechanics.This is an open access article under the CC BY-NC-ND license（http:// creativecommons.org/licenses/by-nc-nd/4.0/）.

Biological flapping flight has been an inspirational source of flightforhumanbeing before the remarkable developmentofmodern fixed-wing aircraft is made.Recently，there is considerable renewed interestto flapping flightin the communities ofaeronautics and flow physics due to the need of developing birdlike micro air vehicles（MAV）［1，2］.Animal flight has been traditionally studied by avian zoologists，and most studies have focused on two groups of flyers:birds and insects.Bats are the only flying mammals that are comparable to small birds in terms of the flight characteristics.However，bats have some unique features that are significantly different from birds，including the special skeletal anatomical structure with more degrees of freedom，highly deformable wingmembrane skin，and more complicated wing kinematics［3］.Bats are more maneuverable and capable in slow flight［4-7］.Compared with a large body of literatures on birds and insects，limited results on bat flight are recently obtained from wing kinematics measurements and particle image velocimetry（PIV）measurements［8-12］. However，a sufficientunderstanding ofthree-dimensional（3D）unsteady flow fields over a flying bat is still lacking.The objective of this work is to conduct numerical simulations of the unsteady flow over a slow-flying bat and investigate the unsteady flow structures and aerodynamic lift generated by the bat flapping wings.

The morphology of the bat wing is reconstructed based on the measurements of Watts et al.［13］，where the outline of the wing at its maximum wingspan is provided.The outline provided by Watts et al.［13］is rescaled based on the relatively positions of the shoulder，wrist，wingtip，5th digit and foot at the instant when the wingspan reaches the maximum according to the kinematics data of Wolf et al.［10］.The rescaled outline of the wing and the coordinate system is shown in Fig.1.The kinematics of the wing in the present numerical model is reconstructed based on the measurements of Wolf et al.［10］，and the motions of the wingtip，wrist，and 5th digit are prescribed while the shoulder and foot are fixed.The other points on the wing are interpolated from the five key points by using the bi-linear interpolation.The motions of the wingtip，wrist，and 5th digit are fitted by using the Fourier series.The trajectories of the wingtip，wrist，and 5th digit in this work are shown in Fig.2 in comparison with those measured by Wolfetal.［10］.The key parameters ofthe modelare listed in Table 1.It is noted thatthe batstudied by Watts etal.［13］forthe wing morphology is the grayheaded flying fox（Pteropus poliocephalus），while the bat studied by Wolf et al.［10］for the wing kinematics is the Pallas long-tongued bats（Glossophaga soricina）.In this sense，the wing geometric and kinematic model in this work is a combination of the two different bat species which serves as a generic bat model.

The flow around the flapping bat wings is obtained by numerically solving the incompressible Navier-Stokes equations.The unsteady flows with the moving boundaries are simulated by using the immersed boundary（IB）method based on the discrete stream function formulation developed by Wang and Zhang［14］.The computational domain used in the present work is［-10c，22c］×［-12c，12c］×［-16c，16c］in the streamwise（x），spanwise（y），and vertical（z）directions，where c is the mean chord length.The unstructured Cartesian mesh with the hanging-nodes is used in the simulations to refine the mesh around the bat model.The minimum grid size is d h=0.02c，and the maximum grid size is d h=0.32c.The time step is selected to keep the Courant-Friedrichs-Lewy numberat0.5.In the simulations，the uniformupstream flow is set at the inlet，and the free convection flow at the outlet.The non-slip boundary condition is specified at the surface ofthe bat model.The zero-shear stress slip wallconditions are used atother boundaries.The initialcondition for the flow is（U∞，0，0）. The independence of the lift coefficient on the grid resolution has been examined.The details of the numerical method and code validations for various flows have been described by Wang and Zhang［14］and Wang et al.［15，16］.In this work，the Reynolds number based on the mean chord length c and the freestream velocity U∞is Re=U∞c/ν=1000 and the Strouhal number is St=fA/U∞=1.36，where f is the flapping frequency.

Figure 3 shows the top views of the vortical structures around the flapping bat wings at four different phases of a flapping cycle（the start of downstroke，middle of downstroke，start of upstroke，and middle of upstroke），where the vortical structures are identified using theλ2-criterion［17］and colored by the streamwise vorticity.The distinct features are the leading-edge vortices（LEVs）generated in the downstroke that are responsible to the vortex lift generation.In contrast，there is no strong and coherent LEV generated in the upstroke.This observation is consistent with the previous reports that the stable LEVs correspond to high lift generation［12］.Figure 4 shows the spanwise vorticity distributions in three spanwise slices when the bat wingspan reaches the maximumin the downstroke.The flow fields in the left column are from the PIV measurements of a Pallas long-tongued bat at 1.5 m/s by Muijres et al.［12］.The flow fields in the right column are from the DNS in the present model at a speed of 1 m/s.It is found the vorticity distributions in the three spanwise slices obtained fromthe DNS are very similar to those obtained in the PIVmeasurements by Muijres et al.［12］.The vortex shedding from the leading edge on the upper surface can be observed in both the DNS and measurements，which considerably contribute the vortex lift generation.The wake structures are also similar in the DNS and measurements.

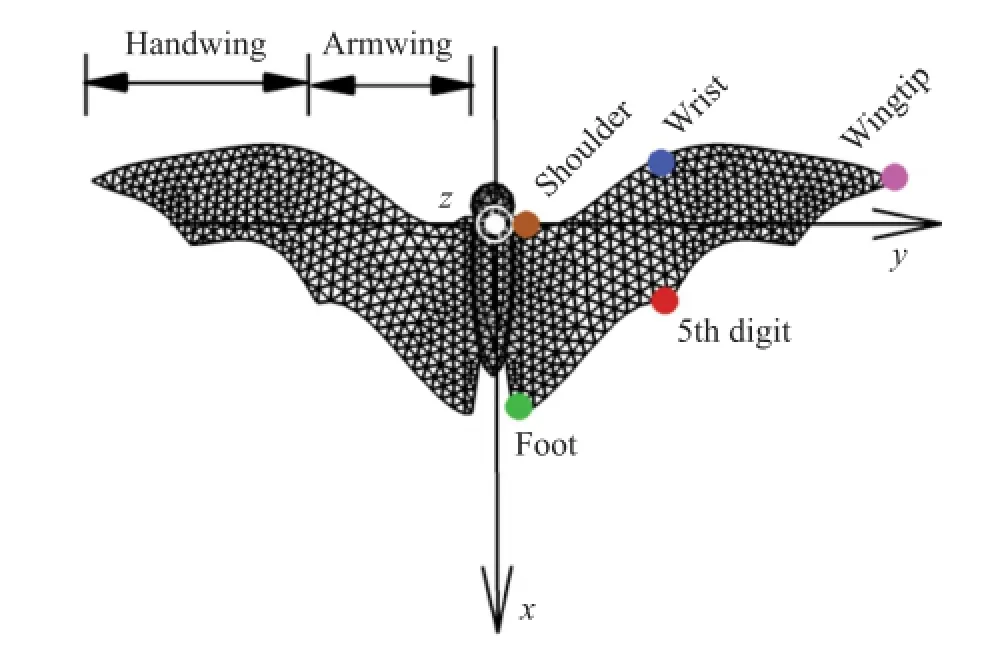
Fig.1.The rescaled outline of the bat wing based on the measurements of Watts et al.［13］.

Table 1Key parameters of the bat model.

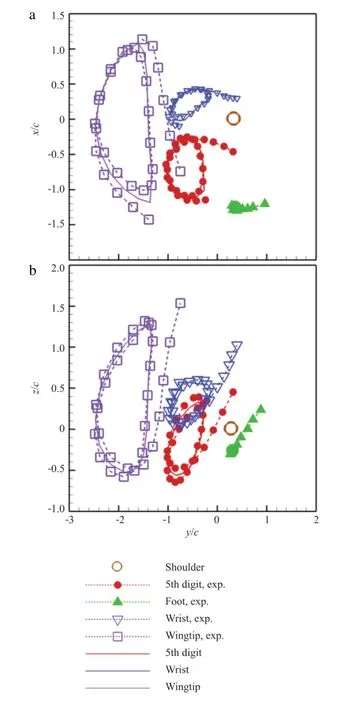
Fig.2.Trajectories of the wingtip，wrist，and 5th digit used in the present work in comparison with those provided in the measurements of Wolf et al.［10］in（a）x-y plane and（b）z-y plane.The brown point is at（0，0.15，0），which is the position of the shoulder.

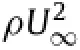
To elucidate the relationship between the lift generation and the vortical structures，the lift decomposition is applied.For a columnar control volume whose upper and lower faces are sufficiently far away from a wing and the vertical faces enclose all the vortical structures between the leading and trailing edges of the wing，the simple lift formula for forward flight is given in the two dominant terms，i.e.，L≈Lvor+Lacc［15］.The vortex lift is

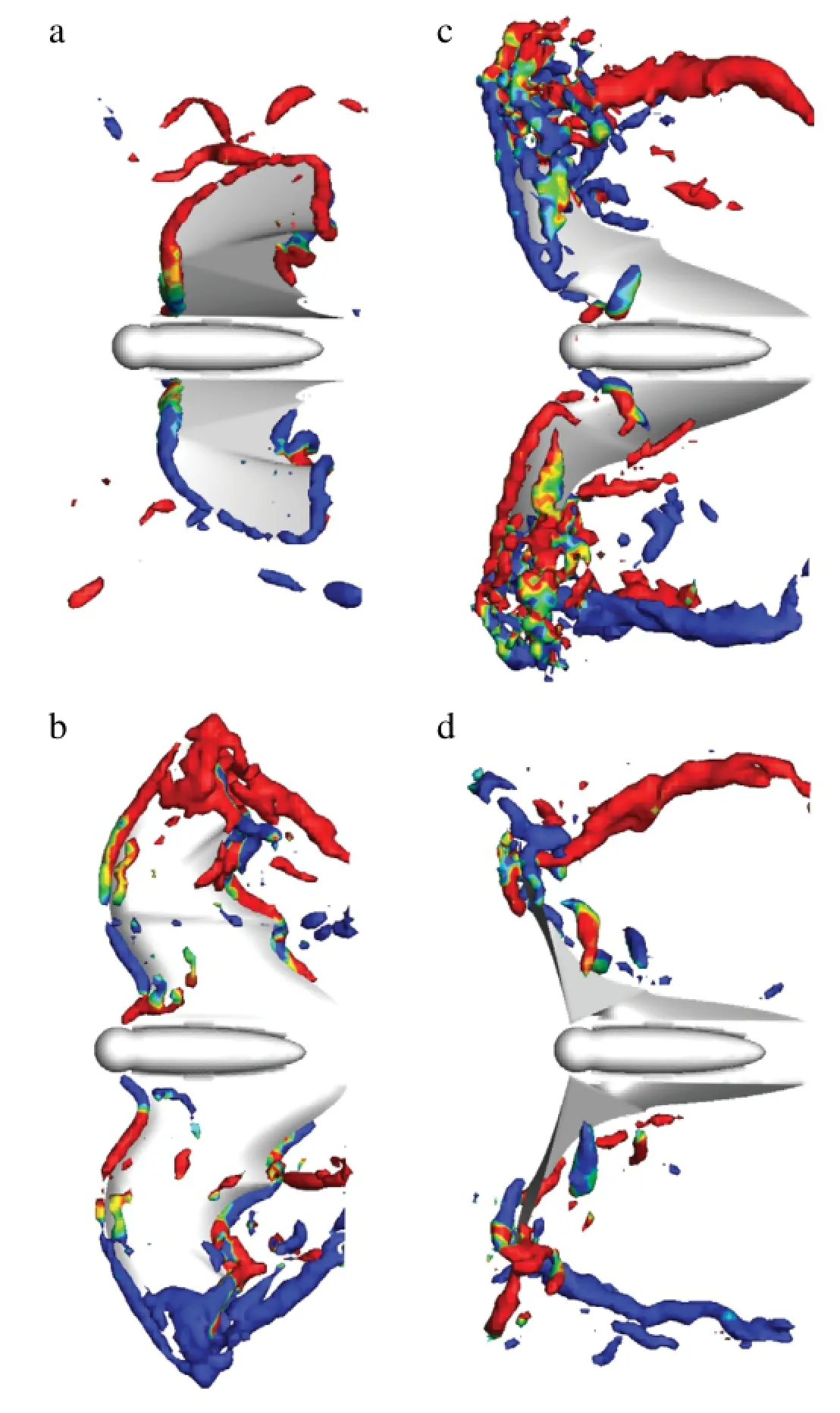
Fig.3.（Color online）The vortical structures around the slow-flying bat at（a）start of downstroke，（b）middle of downstroke，（c）start of upstroke，（d）middle of upstroke.The vortical structures are identified by using theλ2-criterion（λ2= -150）.The color shows the streamwise vorticity.

and the lift associated with the fluid acceleration is

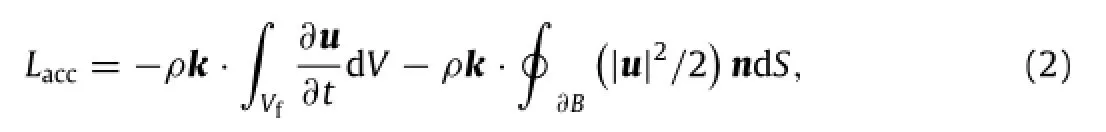
where u is the velocity，ωis the vorticity，q=|u|is the velocity magnitude，Vfdenotes the rectangular control volume of fluid，∂B denotes the boundary of the wing domain，k is the unit vector normal to the freestream velocity，and n is the unit normal vector pointing to the inside of the wing body.The volume integral of the Lamb vector u×ωin Eq.（1）represents the vortex force.In general，Lacccontains the contributions from the fluid motion induced by a moving body and all other intrinsic unsteady phenomena.In the limiting case where the flow is inviscid and irrotational，Laccis reduced to the added-mass lift.The coefficients of the vortex lift and the lift associated with the fluid acceleration are defined as Clvor=Lvor/（q∞Savg）and Clacc=Lacc/（q∞Savg），respectively.The time histories of Clvorand Claccin one flapping period are shown in Fig.5.Interestingly，it is found that the vortex lift coefficient Clvoris positive in both the downstroke and upstroke，indicating that the LEVs can still contribute lift generation even when they are detached from the wing in the upstroke.The time-averaged vortex lift coefficient of the flying bat is〈Clvor〉T=9.2 that is about 71%of the total time-averaged lift coefficient.As observed in Fig.5，Claccis positive in the downstroke and negative in most of the upstroke，and it has also the positive contribution to the time-averaged lift. The time-averaged value is〈Clacc〉T=3.7 that is about 29%of the total time-averaged lift coefficient.

In summary，the numerical simulation indicates that the LEVs generated particularly in the downstroke are the main flow structures contributing the lift generation of the slow-flying bat.The lift can be decomposed into the vortex lift and the lift associated with the fluid acceleration.The vortex lift is dominant in the bat flight，which remains positive in not only the downstroke but also upstroke.In addition，the lift associated with the fluid acceleration contributes the time-averaged lift largely due to the added-mass force associated with the unique geometry and kinematics of the bat wings.

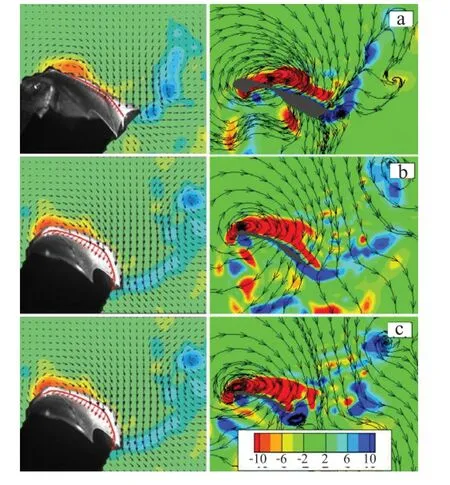
Fig.4.（Coloronline）The distributions ofspanwise vorticity when the batwingspan reaches the maximum in the downstroke in 3 different spanwise slices at（a）35%，（b）50%，（c）65%of the semi-wingspan，respectively.The flow fields in the left column are obtained from the PIV measurements of a Pallas long-tongued bat at 1.5 m/s by Muijres et al.［12］.The flow fields in the right column are obtained from the DNS in the present model at a speed of 1 m/s.

Fig.5.Time histories of the lift coefficients of the flying bat in one period.

Acknowledgments

This work was supported by the National Natural Science Foundation of China（10872201，11232011，11302238，and 11372331），and the National Basic Research Program of China（973 Program）（2013CB834100）（Nonlinear science）.Tianshu Liu would like to acknowledge the hospitality received at LNM during his visit where he accomplished this work.The simulations were performed on TianHe-1.We would like to acknowledge the support from the National Supercomputer Center in Tianjin.

［1］M.F.Platzer，K.D.Jones，J.Young，S.Lai，Flapping wing aerodynamics:progress and challenges，AIAA J.46（2008）2136-2149.

［2］W.Shyy，Y.Lian，J.Tang，D.Viieru，H.Liu，Aerodynamics of Low Reynolds Number Flyers，Cambridge University Press，Cambridge，2008.

［3］A.Hedenstrom，L.C.Johansson，G.R.Spedding，Bird or bat:comparing airframe design and flight performance，Bioinspir.Biomim.4（2009）015001.

［4］Y.Winter，C.Voigt，O.Von Helversen，Gas exchange during hovering flight in a nectar-feeding bat Glossophaga soricina，J.Exp.Biol.201（1998）237-244.

［5］C.C.Voigt，Y.Winter，Energetic cost of hovering flight in nectar-feeding bats（Phyllostomidae:Glossophaginae）and its scaling in moths，birds and bats，J.Comparative Physiology B-Biochemical Systemic and Environmental 169（1999）38-48.

［6］E.F.Stockwell，Morphology and flight maneuverability in New World leafnosed bats（Chiroptera:Phyllostomidae），J.Zool.254（2001）505-514.

［7］S.Swartz，R.Galvao，J.Iriarte-Diaz，E.Israeli，K.Middleton，R.Roemer，X.Tian，K.Breuer，Unique characteristics of aerodynamics of bat flight evidence from direct visualization of patterns of airflow in the wakes of naturally flying bats，Integr.Comp.Biol.45（2005）1080-1080.

［8］X.D.Tian，J.Iriarte-Diaz，K.Middleton，R.Galvao，E.Israeli，A.Roemer，A.Sullivan，A.Song，S.Swartz，K.Breuer，Direct measurements of the kinematics and dynamics of bat flight，Bioinspir.Biomim.1（2006）S10-S18.

［9］T.Y.Hubel，N.I.Hristov，S.M.Swartz，K.S.Breuer，Time-resolved wake structure and kinematics of bat flight，Exp.Fluids 46（2009）933-943.

［10］M.Wolf，L.C.Johansson，R.von Busse，Y.Winter，A.Hedenstrom，Kinematics of flight and the relationship to the vortex wake of a Pallas'long tongued bat（Glossophaga soricina），J.Exp.Biol.213（2010）2142-2153.

［11］A.Hedenstrom，L.C.Johansson，M.Wolf，R.von Busse，Y.Winter，G.R.Spedding，Bat flight generates complex aerodynamic tracks，Science 316（2007）894-897.

［12］F.T.Muijres，L.C.Johansson，R.Barfield，M.Wolf，G.R.Spedding，A.Hedenstrom，Leading-edge vortex improves lift in slow-flying bats，Science 319（2008）1250-1253.

［13］P.Watts，E.J.Mitchell，S.M.Swartz，A computational model for estimating the mechanics of horizontal flapping flight in bats:Model description and validation，J.Exp.Biol.204（2001）2873-2898.

［14］S.Wang，X.Zhang，An immersed boundary method based on discrete stream function formulation for two-and three-dimensional incompressible flows，J.Comput.Phys.230（2011）3479-3499.

［15］S.Wang，X.Zhang，G.He，T.Liu，A liftformula applied to low-Reynolds-number unsteady flows，Phys.Fluids 25（2013）093605.

［16］S.Wang，G.He，X.Zhang，Parallel computing strategy for a flow solver based on immersed boundary method and discrete stream-function formulation，Comput.&Fluids 88（2013）210-224.

［17］J.Jeong，F.Hussain，On the identification of a vortex，J.Fluid Mech.285（1995）69-94.

［18］K.Viswanath，K.Nagendra，J.Cotter，M.Frauenthal，D.Tafti，Straight-line climbing flight aerodynamics of a fruit bat，Phys.Fluids 26（2014）021901.

∗Corresponding author.Tel.:+86 10 82543969.

E-mail address：hgw@lnm.imech.ac.cn（G.He）.

*This article belongs to the Fluid Mechanics