一种扫描式六象限激光探测系统弹目交会算法研究

李元，李燕华，李洛，郭海超，张彦梅，温玉全

（1.北京理工大学爆炸科学与技术国家重点实验室，北京100081；2.北京理工大学信息与电子学院，北京100081）

一种扫描式六象限激光探测系统弹目交会算法研究

李元1，李燕华1，李洛1，郭海超2，张彦梅2，温玉全1

（1.北京理工大学爆炸科学与技术国家重点实验室，北京100081；2.北京理工大学信息与电子学院，北京100081）

针对某旋转式火箭弹定向战斗部定向探测与起爆控制系统，分析了扫描式六象限激光探测系统的构成和工作原理，提出了由激光束螺旋角计算弹体转速的方法，建立了弹体转速数学模型、弹目相对运动方程及相互间的迭代解耦算法，并编写Fortran程序进行仿真。仿真结果表明，建立的交会算法可以计算得到弹体转速、弹目相对运动速度、目标脱靶量、最佳起爆延迟时间、最佳起爆方位角等参量，且误差分析显示探测方位角误差满足定向战斗部的方位探测精度要求。

兵器科学与技术；定向战斗部；弹目交会；多象限激光近炸引信；最佳起爆延时；最佳起爆方位角

0 引言

定向战斗部是一种新型战斗部体制，它可以根据目标相对于弹体的方位，激发相应的起爆序列，使更具威力的毁伤元瞄准并打击目标，提高对目标的毁伤概率［1］。定向战斗部对引信探测提出了新的要求，不仅要求探测系统具有较高的精度和抗干扰能力，而且要能够准确识别目标的方位［2］。采用激光探测器组成周视激光探测系统，是一种较好的解决方案。激光引信利用了激光的良好传输性能，具有较高的距离探测精度和抗干扰性能，而由多个激光探测器组成周向激光探测近炸引信，可以比较精确地探测目标的相对方位角度和距离［3］。研究激光探测体制的弹目交会算法对提高定向战斗部的打击精度、增强定向战斗部的毁伤威力具有重要的理论和指导意义。

本文针对某旋转式火箭弹定向战斗部对定向探测与起爆控制系统的要求，对一种扫描式六象限激光近炸引信探测系统进行了研究，提出了在探测系统设计中增设激光束螺旋角，由激光束螺旋角计算弹体转速的方法，给出了计算弹体转速的数学模型及弹目相对运动方程，并采用迭代法计算了弹体转速、弹目相对运动速度、目标脱靶量、最佳起爆延迟时间、最佳起爆方位角等参量，为进一步应用研究提供了理论依据。

1 扫描式六象限激光探测系统构成及工作原理

1.1 系统构成

本文所研究的六象限激光探测系统如图1所示，由6个激光探测器和相应解算软件组成。6个激光器分为前后两组，构成双探测面的探测系统，其中前3个激光器的光束与弹体轴线构成30°倾角；后3个激光器光束辐射锥角增大，与轴线成45°倾角。同时在设计时，将6个激光探测器围绕弹体轴线螺旋一定的角度。探测系统的转动由火箭弹的旋转提供，使六束激光在空间旋转扫描，构成两锥角的双路探测系统。图1同时示出了偏心起爆式定向战斗部，以及其起爆序列布置［4］。

图1 激光器布置示意图Fig.1 Laser range-finder layout

1.2 工作原理

当目标进入激光探测器的探测距离内时，假如前向激光器首先探测到目标，并在很短的时间间隔内两次探测目标距离，由转速算法（见第2节）解算出弹体在此时的自转速度，同时得到一组目标距离和方位信息。当目标继续相对运动，被后向的激光探测到时，可得到另一组目标的距离和方位信息，探测示意图如图2所示。解算程序根据两次探测到目标的距离和方位角度信息、探测时间间隔以及弹体自身的转动速度，可以计算出目标相对于弹体的运动轨迹，继而计算战斗部的最佳延时时间和最佳起爆方位。

图2 探测目标示意图Fig.2 Schematic diagram of target detection

2 弹体转速的测量

2.1 自转速度测量

激光器相对于轴线的螺旋布置可以使同一激光器短时间内探测到的两个距离信号转换为角度信息，从而实现弹目交会时弹体转速的实时测量。如图3所示弹体三维直角坐标系OXYZ，以探测系统中心O为原点，弹体轴线为Z轴，弹头方向为正，为研究方便，以第一次探测到目标的位置点A与Z轴构成OXZ平面，Y轴由左手直角坐标系确定。O1为激光探测器的激光发射源，O1A代表激光束，K点为第二次探测目标的位置，M和F点分别为A点和K点在OXY平面上的投影。图中虚线矩形所框平面为过激光束且与OXY垂直的平面，此平面与OO1直线的夹角δ即为所定义的激光束的螺旋角，当δ角为0°时，激光探测器变为普通的布置形式。激光束O1A与弹轴的夹角α为激光器的视线角。

这样同一激光探测器两次探测距离的变化量|AK|就和角度的变化量∠MOF建立了一一对应的关系。这在没有激光器螺旋角δ的情况下是无法实现的。

对于一定的目标类型和弹目交会情况（非高速的弹目交会［5］），设某激光器探测到目标，并在很短的时间间隔Δt内测得两次目标距离信息为O1A和O1K，如图3所示，且距离变化为从A到K.考虑到目标的表面积相对于激光束光斑来说比较大，两次测量间隔Δt又非常小，可以认为目标表面形状对探测距离变化的影响非常小，从而可把测量距离的变化归结于弹体的转动和目标的相对运动（交会段一般假设为匀速直线运动）这两个因素。假设目标相对运动造成的探测距离变化表现在图3中为|AG|，那么剔除这部分距离变化，剩余的距离变化|GK|= |AK|-|AG|则是由弹体自身转动引起的。

|AG|可由相对运动方程计算得到，那么根据两次探测距离变化|AK|和探测时间Δt，并结合探测系统参数信息，可以计算由弹体转身引起的距离变化|GK|所对应的角度∠NOF（如图3中示），此角度即为弹体转过角度，除以时间Δt即可得到弹体自转速度ω.

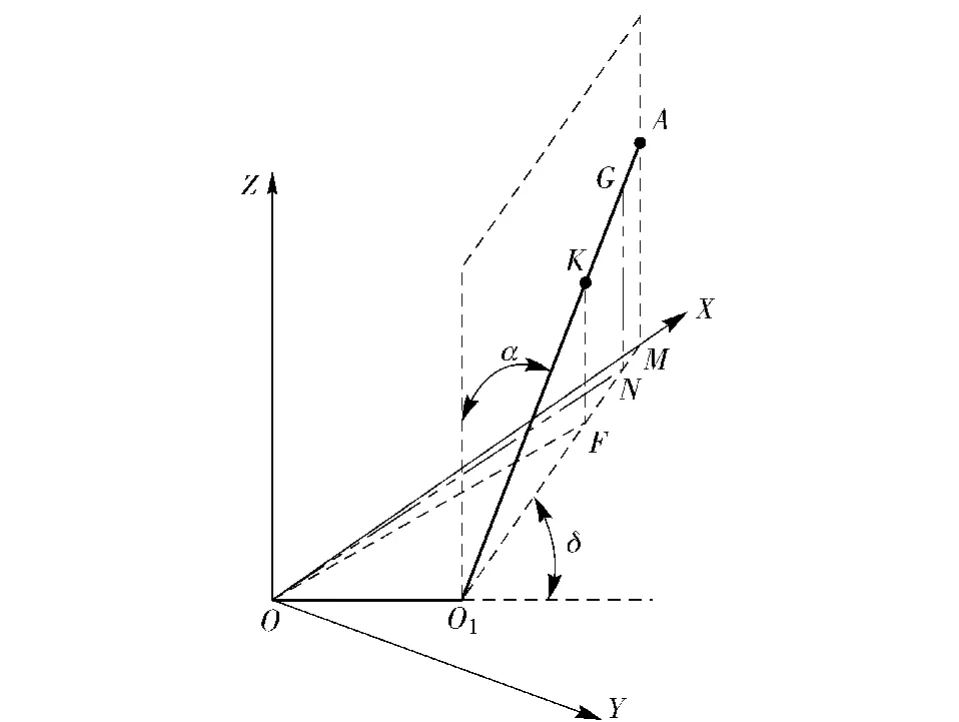
图3 转速自测量原理图Fig.3 Schematic diagram of rotational speed

图3中，虚线矩形所示平面内，设|O1A|=LO1A（下文式中有关距离的量都由此方法表示），则

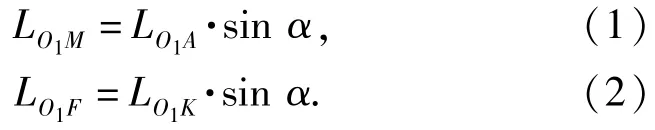
在三角形OO1M中，已知距离|O1O|、角度δ，则根据余弦定理有

根据正弦定理

联立（1）式、（3）式、（4）式得

同理，在三角形OO1F中，

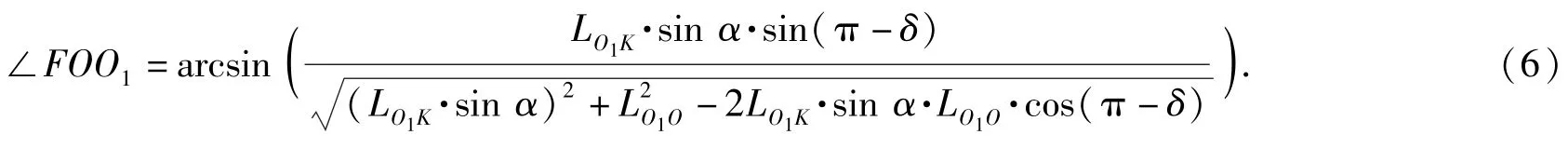
那么有

∠MOF即为激光探测器探测到的目标距离变化|AK|所对应的角度。

同理

式中:LAG为目标相对运动引起的距离变化|AG|，需要由相对运动方程解出。那么∠NOF即为除去目标相对运动引起的距离变化外，剩余的距离变化所对应的由弹体转动引起的角度变化。弹体转速即可由下式计算:

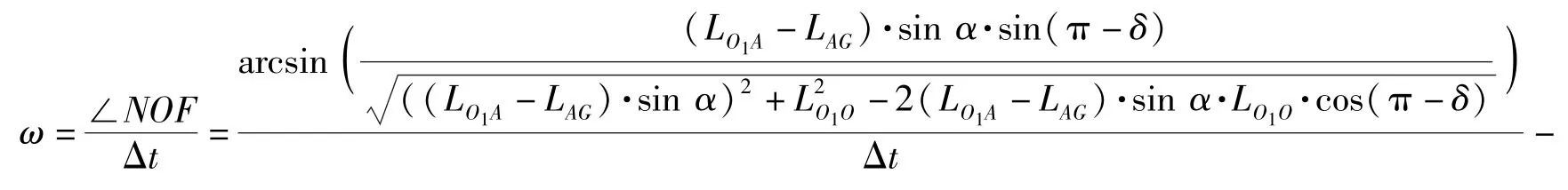
2.2 螺旋角的设计与选取

由于激光探测器螺旋角δ的存在，使得可以通过（7）式将激光探测距离的变化同弹体转动角度联系在一起，从而可以实现弹体转速的测量。δ的取值大小关系到由于探测距离变化而导致的转动角度大小的显著性，从而会影响到转速的测量精度。

设定探测到的距离变化|AK|保持不变，如图3所示，则与之相对应的角度变化∠MOF越大，转速就越容易测量，测量精度也越高。根据（7）式，当其他参数不变的情况下，角度变化∠MOF仅是螺旋角δ的函数。设∠MOF为因变量f（x），螺旋角δ为自变量x，且x∈（0，π/2），则有

式中:LO1O、α为弹体参数；LO1A、LO1K为探测距离。在假设|AK|的值不变的情况下，LO1K=LO1A-LAK.

取一定的LO1A值，则f（x）的函数图形如图4所示。

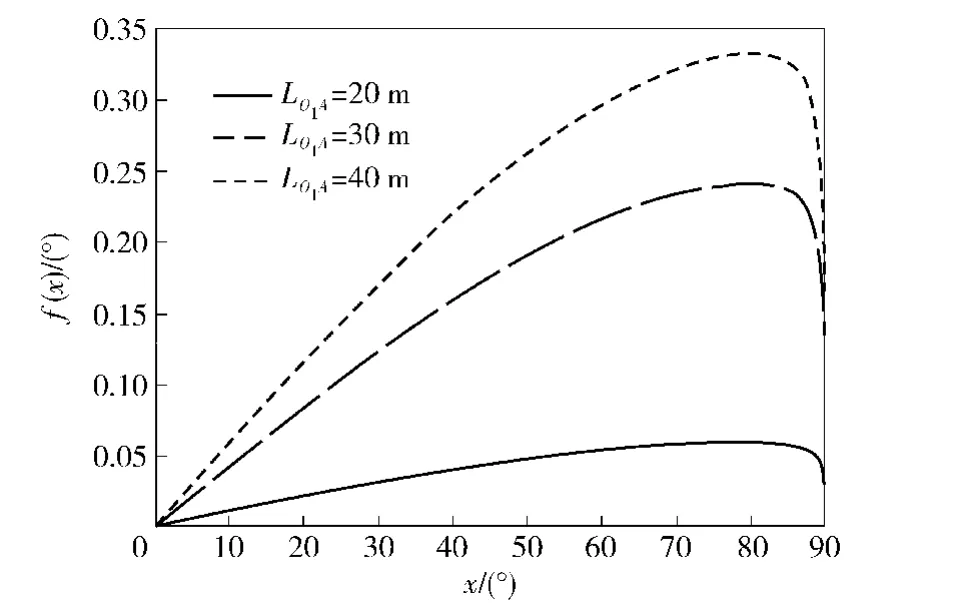
图4 转动角度与螺旋角的关系Fig.4 The relationship between rotational angle and helix angle

由图4可知:对于不同的探测距离，随着探测距离LO1A的增大，转动角度f（x）也增大；当探测距离LO1A一定时，转动角f（x）在（0，π/2）范围内会随着螺旋角的增大而增大，当增大到一定值后，则随着螺旋角增大而减小，所以转动角存在极大值。极大值所对应的x坐标即为最优的螺旋角取值。从图4中可以看出，当螺旋角在70°左右时所对应的旋转角度最大，但是螺旋角的选取还应与战斗部的探测与起爆分位数相匹配，设计时应综合考虑。

3 弹目相对运动模型

为简化计算，在建立弹目交会数学模型时，做如下3条假设:

1）在未考虑弹体自转时，沿用经典假设，认为交会段的很短时间内，目标相对于弹体的运动为匀速直线运动［6］；那么在考虑弹体自转时，目标相对于弹体的运动即为匀速直线运动和匀速圆周运动的合成。

2）为简化分析，将目标简化为点目标。

3）建立最佳起爆延时模型时，不考虑破片速度在空气中的衰减。

3.1 运动方程的建立

弹体转速增加了弹目交会情况的复杂性，为方便研究，建立了弹体坐标系的圆柱坐标系形式（γ，φ，z），如图5所示。

图5 弹目交会图Fig.5 Endgame configuration

以战斗部中心O为坐标原点，弹轴为坐标Z轴，以首次探测到目标的目标位置点A和弹轴组成的平面为φ坐标的起始平面，即图5中的OXZ平面。前后向激光器逆时针螺旋布置，螺旋角为δ.O1A代表首次探测到目标的前向激光器光束，O1B为探测到目标的后向激光器光束；A、B点代表探测到目标时的目标位置点。O1、O2为激光器中心，其到弹轴的距离设为λ.

在弹体坐标系中观察时，目标相对于弹体的运动可分解为匀速直线运动和相对弹体轴线的匀速圆周运动，将这两个运动形式分别向3个柱坐标轴投影可得到3个坐标上的运动分解，并分别建立运动方程，再合成即可得到目标相对运动的参数方程。

对目标的匀速直线运动，设A点的坐标为（x0，y0，z0），则直线运动参数方程为

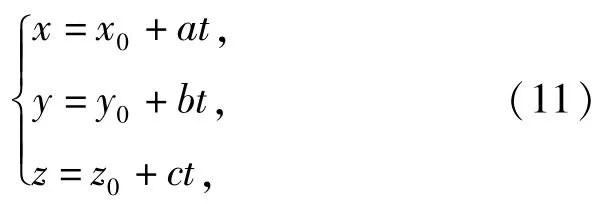
式中:a、b、c分别为直角坐标系3个方向上的运动速度分量。

与匀速圆周运动方程φ=ωt合成，得到柱坐标下目标相对于弹体的参数运动方程，如（13）式所示:

假设目标沿着ABE曲线相对于弹体运动，在A点时被某一前向激光器探测到，经过时间tAB后运动到B点时被后向某一激光器探到（为简化处理，假设两个作用的激光器是相邻的，其他情况可类似处理），那么根据测得的A、B两点的坐标，以及测得的弹体转速ω，可以计算出（12）式运动方程中的3个未知数a、b、c，从而得到目标相对于弹体的运动方程。

3.2 运动方程的求解

设两束激光探测到目标的距离分别为R1、R2，光束倾角α、β.首先根据距离信息计算A点的坐标值，设A点坐标为（x0，y0，z0），则

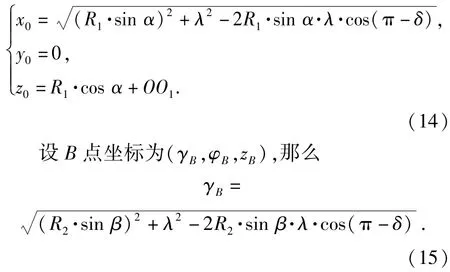
依据上述2.1节有关原理，可以求得图5中O1激光器原点的φ坐标值φ1:

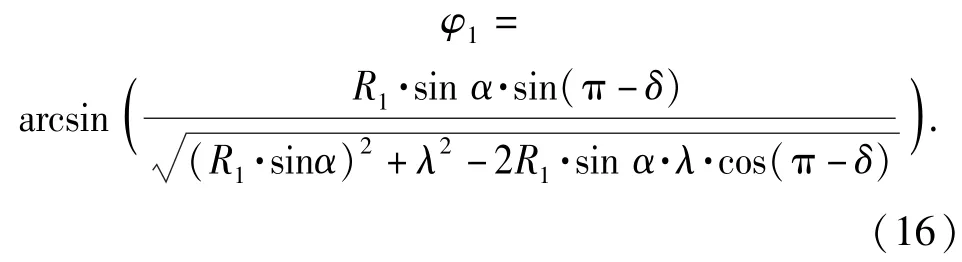
同理，可以求得B点与O2激光器原点之间的φ坐标距离值φ2:

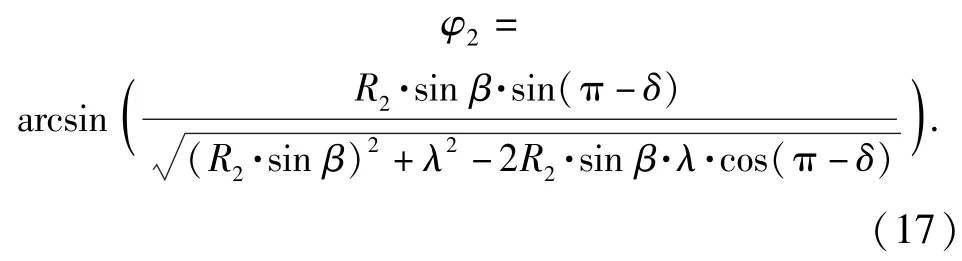
设n为两次探测到目标的时间间隔tAB内弹体转过的圈数，则

那么B点的φ坐标为

对于表 1所列地震的计算结果，MS和 MS(BB)的对比情况如图2所示。图上可以看出，MS震级整体比MS(BB)大，相减之后的结果统计如图 3。MS和 MS(BB)的差值分布在0.0和0.3之间。差值在0.2的地震个数最多，为28个，占到总数的66.67%；差值在0.3和0.1的地震共有12个，占总数的 28.57%；差值在 0.0的地震共有 2个，占总数的4.76%。平均差值为0.195。

B点的Z坐标为

将（14）式、（15）式、（19）式、（20）式以及tAB代入（13）式中，联立求解，可得

设ε为φB-ω·tAB对2π的余数，则

将求得的a、b、c带入（13）式，即可得到目标相对弹体的运动方程。

由第2节可知，转速的测量需要知道由相对运动引起的距离LAG，此值可以由（21）式、（22）式、（23）式求得的相对运动方程求得。然而，相对运动方程的求解又依赖于弹体的转速值，因此转速的测量和相对运动方程的求解是一个相互耦合的过程。对于此问题，可使用循环迭代方法进行计算。

4 战斗部最佳起爆延时和起爆方位计算

对于侧向偏心起爆定向战斗部，在战斗部的轴线方向上，中心处的破片速度最高。因此，理想的打击点应位于战斗部中心所在的平面内。假设破片打击到目标的位置为E点，见图5.根据B点的Z坐标和目标相对运动的Z方向速度，可以得到目标从B点运动到打击点E的时间tBE，进而根据运动方程（13）式计算E点的坐标（γE，φE，zE）.

由于zE=0，则

将E点的γ坐标除以破片飞行速度v0，可得破片从战斗部起爆到打击到目标的飞行时间tP，即

那么，根据最佳起爆延时的定义，最佳起爆延时时间子为

5 目标探测物理仿真

5.1 单次仿真计算

针对某一空中目标，设前后激光探测器探测到了目标，探测到的目标距离分别为R1=25 m、R2= 18 m，时间间隔tAB=20 ms.前向激光在探测弹体转速时的探测距离变化LAK=2 m，间隔时间为Δt= 2.6 μs.前向探测激光束倾角为α=30°，后向激光束倾角为β=45°，螺旋角为δ=60°.激光器中心到弹轴的距离为λ=0.05 m，前向激光器中心到战斗部中心的轴向距离OO1=0.36 m，后向激光器中心到战斗部中心的轴向距离OO2=0.24 m.假设前后探测到目标的激光器是相邻的，破片初速为v0= 2 000 m/s.采用耦合迭代算法进行计算，设定转速初始值为50 000 r/min，将以上参数带入第2、3、4节中的公式，编写Fortran程序联立求解可得:测得的弹体自转速度为18.35 r/s；相对速度大小870.40 m/s，x轴速度分量-430.15 m/s，y轴速度分量-606.75 m/s，z轴速度分量-452.14 m/s；脱靶量为18.19 m.

计算得到的战斗部最佳延时时间和起爆方位角:最佳延时时间子=13 ms；最佳起爆方位角φf= 10.05 rad.在规定的延期时间内，引信引爆由最佳起爆方位角所对应的起爆序列，就能使战斗部毁伤效能最大化。

5.2 误差分析

从以上推导过程可知，所建模型的误差主要来自两个方面:一是在转速测量时，忽略了目标表面形状对结果的影响；二是运动方程建立时，未考虑目标的体积效应。

当遭遇大体积目标时，模型误差主要来自第二个方面，即测量点距离目标体中心的长度方向误差。这会导致毁伤元打击到目标中心（或者弹药舱）的前面或后面，而不是正中目标中心，但是由于目标体积大，即使这样也足够摧毁目标。

当弹体所遭遇的目标体积较小时，误差主要来自于第一个方面，即弹体转速的测量误差。此时误差会影响到定向战斗部的目标方位定位精度，不能使最具毁伤威力的破片打击到目标，从而影响毁伤效果。

所建模型误差还来自于以上各方程中相关参数的误差，如激光器探测距离误差、激光器安装角度误差等。根据文献［2］中关于确定定向战斗部定位精度要求的方法，可推知当定向战斗部为六象限起爆时，其破片飞散角的分辨率为30°，方位角的分辨率为10°（安全系数为3）。那么由探测系统导致的方位角误差不应大于10°，即0.175 rad.假设激光器的距离探测精度为±0.015 m，激光束螺旋角的安装误差为1°，那么根据转速公式和相对运动方程可计算转速的测量误差为

方位角的测量误差为

从中可以看出，在此种激光器误差和安装误差下，该引信探测系统的方位角探测精度能够满足六象限定向战斗部的定位要求。

6 结论

本文针对某旋转式火箭弹定向战斗部定向探测与起爆控制系统，提出了在探测系统设计中增设激光束螺旋角、由激光束螺旋角计算弹体转速的方法，给出了计算弹体转速的数学模型、弹目相对运动方程及相互间的耦合迭代算法。

交会仿真结果表明，利用本文所建立的数学模型和方程可以计算弹体转速、弹目相对运动速度、目标脱靶量、最佳起爆延迟时间、最佳起爆方位角等参量，且误差分析得到的方位角探测误差为0.08 rad，满足定向战斗部的方位角探测精度要求。本研究所建交会算法切实可行，可为进一步的应用研究提供理论参考依据。

（

）

［1］ Carleone J.Tactical missile warheads［M］.Washington，DC:A-merican Institute of Aeronautics and Astronautics，Inc.，1993: 444-446.

［2］ Held M.Fuse sensor requirements of different amiable anti air warhead layouts［C］∥23rd International Symposium on Ballistics. Lancaster，PA，US:International Ballistics Committee，2007: 77-87.

［3］ 张正辉，杨明，许志文.激光引信光束布局方式的选择与分析［J］.红外与激光工程，2006，35（6）:700-704. ZHANG Zheng-hui，YANG Ming，XU Zhi-wen.Analysis of FOV configuration in laser proximity fuze［J］.Infrared and Laser Engineering，2006，35（6）:700-704.（in Chinese）

［4］ 温玉全.刚性爆炸网络若干应用研究［D］.北京:北京理工大学，2000. WEN Yu-quan.Research on some issues of the rigid explosive circuit［D］.Beijing:Beijing Institute of Technology，2000.（in Chinese）

［5］ 郭泽荣，李洛，李元.六光束脉冲激光探测定向战斗部最佳起爆延时研究［J］.北京理工大学学报，2014，34（6）:588-591. GUO Ze-rong，LI Luo，LI Yuan.Study on theoptimum time delay of six laser range-finders for aimed warhead［J］.Transactions of Beijing Institute of Technology，2014，34（6）:588-591.（in Chinese）

［6］ 张志鸿，周申生.防空导弹引信与战斗部配合效率和战斗部设计［M］.北京:宇航出版社，1994. ZHANG Zhi-hong，ZHOU Shen-sheng.Anti-air missile fuze warhead cooperation efficiency and warhead design［M］.Beijing: China Astronautics Publishing House，1994.（in Chinese）

Research on Projectile-target Encounter Algorithm for Six-quadrant Scanning Laser Proximity Fuze Sensor

LI Yuan1，LI Yan-hua1，LI Luo1，GUO Hai-chao2，ZHANG Yan-mei2，WEN Yu-quan1
（1.State Key Laboratory of Explosion Science and Technology，Beijing Institute of Technology，Beijing 100081，China；2.School of Information and Electronics，Beijing Institute of Technology，Beijing 100081，China）

Based on the fuze sensor and detonation control system of an aimiable warhead of a spinning rocket，the construction and functional mechanism of the six-quadrant scanning laser fuze sensor is analyzed.A method of measuring the rocket rotational speed based on the spiral angle of laser beam is proposed.A mathematic model of rotational speed and a projectile-target relative motion equation are deduced，which can be solved by iterative decoupling algorithm.Simulation based on the Fortran program is conducted，and the optimal detonation time delay，optimal detonation azimuth angle and miss distance are obtained.The error analysis shows that the detected azimuth error meets the requirement of detecting accuracy.

ordnance science and technology；aimable warhead；projectile-target encounter；multiquadrant laser proximity fuze；optimal detonation time delay；optimal detonation azimuth angle

TJ43+9.2

A

1000-1093（2015）11-2073-07

10.3969/j.issn.1000-1093.2015.11.008

2014-06-13

武器装备预先研究项目（40404010X）

李元（1987—），男，博士研究生。E-mail:panshi-boshi@163.com；温玉全（1965—），男，副教授，博士生导师。E-mail:wyquan@bit.edu.cn