弹药装填系统用蜗式推送链动力学分析
张雷雨,杨洋
(北京航空航天大学机械工程及自动化学院,北京100191)
弹药装填系统用蜗式推送链动力学分析
张雷雨,杨洋
(北京航空航天大学机械工程及自动化学院,北京100191)
推送链机构是一种新型直线伸缩机构,可将弹药从一个位置快速推送至另一位置,具有推送距离长、收回状态占用空间小的优点。该机构采用蜗式链盒存储单向链,能够在有限空间中存储最大数量的链节,实现大距离的推送。为了分析链轮多边形效应和啮合冲击对单向链的动力学特性和推送平稳性的影响,建立了单向链从链盒中抽出过程及与链轮啮合过程的动力学模型,同时,将单向链伸出部分简化为多弹簧阻尼系统,推导出单向链推送过程的动力学模型。借助数学软件MATLAB,采用龙格-库塔法,对推送链机构的整体动力学模型进行数值仿真。仿真结果表明:在推送过程中,将单向链从蜗式链盒中拖出的抽出力随时间震荡减小至0,链轮对单向链的拨动力由剧烈震荡过渡至平稳波动,且单向链的推送速度波动较小,该机构具有良好的推送平稳性。通过试验测量,验证了所建立动力学模型的准确性。
兵器科学与技术;推送链机构;直线伸缩机构;多边形效应;单向链;多弹簧阻尼系统
0 引言
推送链是一种直线伸缩机构,具有送距离长、收回状态占用空间小的优点,在装甲车辆中应用较为广泛,可快速将弹药从药仓推送至炮膛。近年来,国内外学者提出了多种伸缩机构的形式,对伸缩机构的研究也较为成熟。Lee等[1]公开了一种用于桥梁运输系统的伸缩管装置,控制钢丝绳的伸出和收回,实现伸缩管在轴线方向的伸缩。Enders等[2]研制了一种多级伸缩机构,通过注入和放出压力油,完成各级油缸的伸缩。Lee等[3]设计一种由多层平板和钢丝绳组成的绳驱双向伸缩机构,且该机构具有较大的承载能力。剪叉式高空作业平台是一种典型的伸缩机构,平台升起时能够提供稳定的支撑[4]。在上述几种类型中,伸缩机构的基体结构体积庞大,以提供足够的支撑强度;为了确保末端具有足够大运动行程,伸缩部件在缩回状态体积较大,因此,上述伸缩机构很难在有限的约束空间中实现大行程的伸缩。Kawabuchi等[5]提出了一种由多个铰接在一起的物块组成的伸缩机构,伸出的物块由钢丝绳或同步带拉紧,保持刚性连接,实现机构的伸缩功能。该机构具有结构紧凑、占用空间小和安全性高的优点,但是其伸缩速度较低且推送负载较小,无法满足长距离、大推送力的要求。
蜗式推送链机构是一种新型伸缩机构,该机构主要由蜗式链盒、单向链和链轮等组成;与传统链条不同,单向链条为开放式结构,并且链节之间具有单向弯曲特性。在重力作用下,单向链推送弹药时可沿水平方向直线伸出;收回时,单向链的各链节依次卷曲在蜗式链盒中。该机构的结构紧凑、推送力大,且单向链伸出距离与机构收回状态总体长度的比值较其他伸缩机构大,适合在约束空间下大距离推送弹药。
蜗式推送链属于链传动的变胞形式之一,对链传动的动力学性能研究较多。李业农等[6-7]主要进行了推送链负变位设计、运动学分析和运动误差计算,但对推送链的动力学还未涉及。Chew[8]将滚子链中各链节的质量简化至滚子中心,采用归纳法,推导出链条的等效质量公式,得到链条惯性对链节间冲击强度的影响。Troedsson等[9-10]着重分析链传动中静载荷的分布和链条震荡问题,将链节等效为具有弹簧阻尼特性的弹性链板,建立了链传动的整体动力学模型。Zheng等[11]采用显式有限元方法,建立了链传动的全尺寸模型,分析了滚子链的机械特性和啮合时的瞬态震动响应。Xu等[12-13]在建立滚子链的动力学模型时,考虑了输入轴的弹性和链条中间隙的影响。上述研究均是针对传统的封闭滚子链传动,而单向链为开式链,且对单向链的动力学研究还未见到。
借鉴上述分析方法,分析链轮多边形效应和啮合冲击对推送平稳性的影响,建立了单向链从链盒中抽出过程及与链轮啮合过程的动力学模型,同时,将单向链伸出部分简化为多弹簧阻尼系统,推导出单向链推送过程的动力学模型。借助数学软件MATLAB,采用龙格-库塔法,对推送链机构的整体动力学模型进行数值仿真,分析该机构的动力学特性和推送平稳性。
1 推送链机构的结构和工作原理
蜗式推送链由蜗式链盒、单向链、链轮及导向槽等组成,如图1所示,链盒中的储链轨道为阿基米德螺线,能够在有限空间中储存尽可能多的链条。链轮轴上安装有两个相同链轮,且固连在一起形成双链轮,双链轮与链条上的双排滚子啮合,轮齿为“圆弧-圆弧”齿廓。链轮逆时针旋转时,链轮将单向链从链盒中拨出,单向链沿着导向槽直线伸出。单向链条收回时,在导向槽的导向作用下,链轮顺时针转动并且拨动单向链,强制单向链沿着螺旋轨道运动,单向链逐圈储存起来。
单向链由双排滚子、套筒、链板、销轴和垫圈组成,如图2所示,单向链中内、外链板通过铰链的形式连接,在水平位置时,链板在铰链处具有单向性,仅能绕铰链圆心O逆时针转动;单向链水平伸出时,链板受到重力作用,链板底部的接触面(见图2)相互抵靠,阻止链板绕O点顺时针转动,伸出的链板保持近似刚性连接。
推送过程中,单向链受到螺旋轨道的运动阻力及链轮多边形效应的作用,且单向链伸出部分具有一定弹簧阻尼特性,因此,单向链的动力学响应和推送平稳性是本文的研究重点。
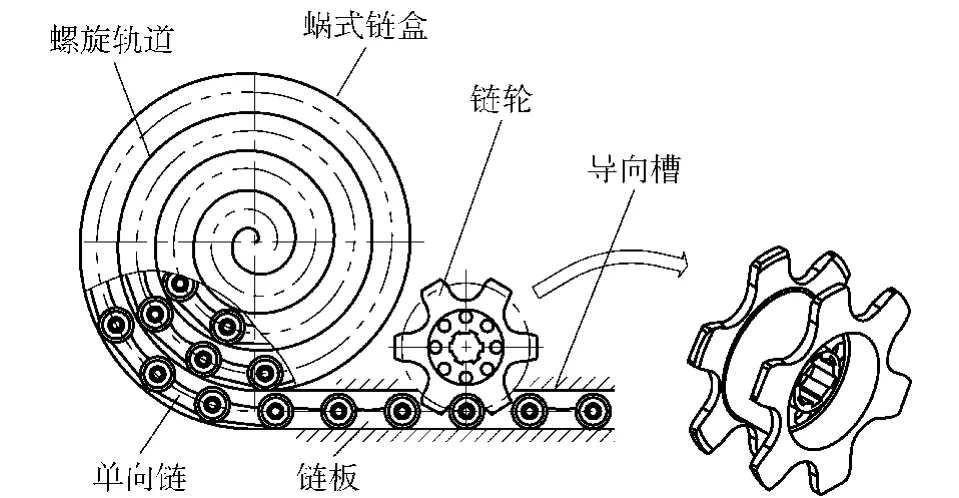
图1 蜗式推送链的结构模型Fig.1 Structure of helicoid pushing chain mechanism
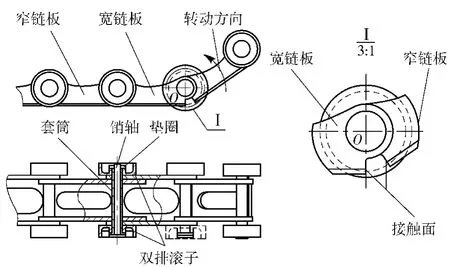
图2 单向链的结构模型Fig.2 Structure of unidirectional chain
2 蜗式推送链的动力学建模
推送链工作时,单向链中各链节经历3个过程:从蜗式链盒中抽出、与链轮啮合、沿导向槽伸出,链首与弹药底部接触开始推送,弹药沿轨道水平直线运动。假定弹药与轨道之间的运动阻力恒定,该运动阻力等于单向链的推送力Fpu,因此,动力学模型主要包括三部分:单向链抽出模型、单向链与链轮啮合模型及单向链推送模型。
为了便于分析,将套筒、链板、销轴和垫圈的总质量m集中在双排滚子的中心,单向链即被简化为一串铰接的质点。同时,做出以下假设:
1)所有链节具有相同的质量、刚度和节距;
2)忽略单向链在竖直方向上的震动;
3)忽略铰链间隙、单向链与链盒间的间隙。
2.1 单向链抽出过程的建模
单向链的各链节均匀分布在蜗式链盒中,链盒储链轨道间距为2πa,与双排滚子的直径相等,如图3所示,在极点为O、极轴为X的极坐标系下,滚子中心所在的阿基米德螺线的方程式为
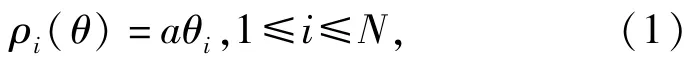
式中:ρi为滚子圆心Oi的极径;a为阿基米德螺线系数;θi为极角;N为蜗式链盒中存储链节的总数。
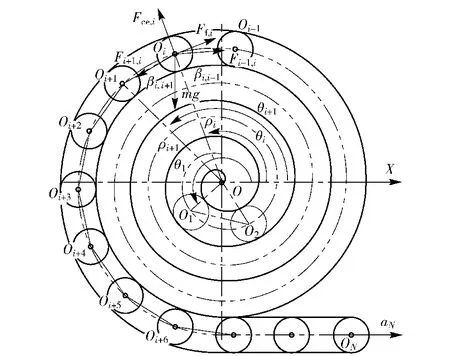
图3 单向链在链盒中的排布Fig.3 Configuration of unidirectional chains in helicoid chain case
单向链的起始端处滚子中心坐标为(ρ1,θ1),滚子i和i+1中心坐标分别为(ρi,θi)和(ρi+1,θi+1),ρi与ρi+1的夹角为Δi,i+1,点O、Oi、Oi+1组成封闭的三角形,根据三角函数定理,可得

式中:P为链节的节距,且θi<θi+1.采用递推法,由(1)式、(2)式依次得到θ2,θ3,…,θN,各链节的坐标位置即可实时确定。
蜗式推送链推送弹药时,链轮拨动单向链,单向链从链盒中快速抽出,且各滚子沿螺线的切向速度及切向加速度相等。在链盒中滚子i受到滚子i+1的正向拉力Fi+1,i和滚子i-1的反向拉力Fi-1,i,滚子i还受到离心力Fce,i和摩擦阻力Ff,i,如图3所示。以滚子i为研究对象,建立沿螺线切向的动力学平衡方程:
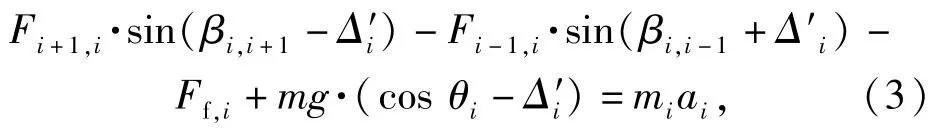
式中:ai为滚子i沿螺线切线方向的加速度;为螺线切线在Oi处与ρi垂线的夹角;βi,i-1、βi,i+1分别为ρi与Fi-1,i、Fi+1,i的夹角,且

若离心力Fce,i占主导因素,在轨道运动中的滚子i则与轨道外侧挤压,否则与轨道内侧接触,但Ff,i始终与滚子i运动方向相反,因此,Ff,i的数值为

式中:μ为滚子i与链盒的摩擦系数,且
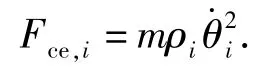
在已知加速度ai的情况下,联立(3)式、(4)式,借助各链节的坐标位置,采用递推法求解,依次求出链节间的相互作用力F2,1,F3,2,…,FN,N-1.
2.2 链轮与单向链啮合过程的建模
在推送弹药过程中,单向链与链轮啮合,在链轮齿的拨动下沿导向槽直线运动,链轮的转动中心为Od,节圆半径为rd,齿侧圆弧半径re与滚子定位圆弧半径rb之和等于链轮节距P,与滚子j+1啮合的定位圆弧中心为Od,j+1,相对应滚子j+1的中心为,如图4所示。
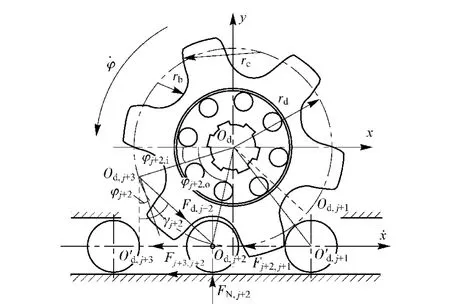
图4 链轮与单向链的啮合动力学模型Fig.4 Meshing dynamics model of sprocket and unidirectional chain
链轮拨动滚子j+1时,滚子j+1前进一个节距P,链轮的转角φ转动一个节距角,链轮的角速度为,为了便于分析,转角φ定义为链轮在坐标系Odxy第三象限中转过的角度。滚子j+2即将进入啮合状态时,链轮齿对滚子j+2的拨动力为Fd,j+2,方向由点Od,j+3指向Od,j+2,将线段OdOd,j+3与x轴的夹角φj+2,i定义为滚子j+2的啮入角,OdOd,j+2与x轴的夹角φj+2,o为啮出角。滚子j+2进入啮合状态后,滚子受到外负载的作用,如单向链的抽出力、弹药的运动阻力等,且链轮对滚子的作用力Fd,j+2的方向随着转动角度发生变化,滚子j+2在啮合位置受力较为复杂。
根据机构动力学,可推导出单向链伸出速度x·与链轮角速度的关系为

在啮合过程中,以滚子j+2为研究对象,滚子j+2的动力学平衡方程为

式中:Fj+2,j+3为滚子j+3对滚子j+2的拉力;Fj+2,j+1为滚子j+1对滚子j+2的阻力;FN,j+2为滚子j+2对导向槽的压力;Ff,j+2为滚子j+2对导向槽摩擦阻力,且满足Ff,j+2=μFN,j+2,γj+2为Fd,j+2与竖直方向的夹角。
驱动力Fd,j+2与电机功率有关,Fd,j+2与链轮转速存在以下关系:

式中:φj+2为链轮拨动滚子j+2时转动的角度,且满足γj+2=arccos(1-sin φj+2);ρpo为驱动功率。
在单向链运动过程中,滚子i的加速度ai与滚子j+2的加速度相等。因此,在Fj+2,j+1已知和驱动功率Ppo恒定的情况下,可将(5)式和(7)式代入(6)式进行求解,得到滚子j+2的速度和加速度响应。
2.3 单向链推送过程的动力学模型
坦克炮塔回位之后,当炮膛轴线与药仓的供弹线对齐时,推送链将储弹筒中的弹药直线推送至炮膛。坦克在行进过程中,在道路存在上、下坡时,弹药的推送通道与水平线产生推送夹角ψ,夹角ψ影响推送链的推送性能。在推送过程中,链首与弹药尾部接触且不发生相对滑动,单向链受到导向槽和弹药尾部的约束力,单向链近似为由多链节刚性连接的弹性杆。为了准确计算单向链的推送动力学响应,将各链节简化为弹性阻尼单元[14],采用数轴法,建立伸出部分的多弹簧阻尼系统数学模型,如图5所示。建立推送数轴Ox,Ox平行于推送通道,当ψ=0°时,Ox平行于水平方向,用xj表示滚子j在数轴Ox中的坐标位置,采用归纳法分析单向链的动力学响应。
以链节1为研究对象,此时的动力学方程为
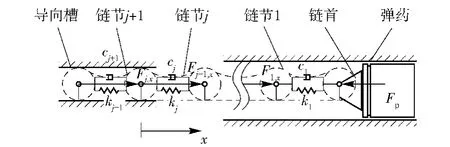
图5 单向链的推送动力学模型Fig.5 Pushing dynamics model of unidirectional chain
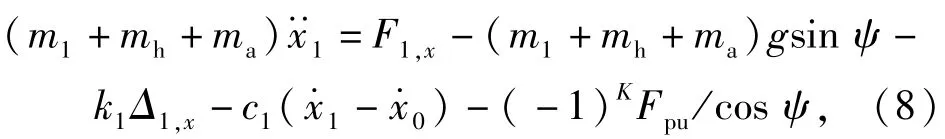
式中:K为工况系数;x1和x0分别为滚子1和链首的坐标位置和关于时间t的函数;F1,x为链节2对链节1在x轴方向的推力;mh为链首质量;ma为弹药质量;k1和c1分别为链节1的弹簧刚度和阻尼系数;Δ1,x=l-(x0-x1),l为单向链的节距。当推送通道水平时,K=0;坦克上坡工况时,K=1;坦克下坡工况时,K=2.
由图4可知,此时链节2刚与链轮脱开啮合状态,链节3即将进入啮合状态,由此可得

依次类推可得到Fj+2,j+1的表达式:

联立(3)式、(5)式、(6)式、(7)式及(8)式,即可求解链首的速度和加速度响应。
根据完整归纳法,可以得到前j节链节的动力学方程:

式中:Δj,x=l-(xj-1-xj);Ff,j+1为链节j+1与导向槽摩擦阻力,这是由伸出的j节链条对链节j+1产生较大的翻转力矩产生的,即
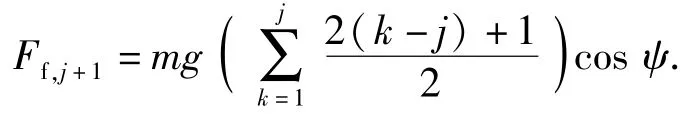
3 数值仿真
在上部分中,蜗式推送链的动力学方程分为三部分:单向链抽出过程、啮合过程及单向链推送过程,由于每部分的动力学方程均含有其他部分的参数,因此,进行动力学求解时,需要将三部分联立求解。上文的动力学方程均含有2阶微分方程,借助数学软件MATLAB,采用龙格-库塔法进行求解。
单向链在推送过程中,拉力Fi,i-1和推力Fj,x在每步计算中都会发生变化,且大小取决于单向链推送的速度和加速度.由于单向链伸出部分简化为多弹簧阻尼系统,动力学方程(9)式含有j个方程和2j个未知数,联立(3)式、(6)式、(7)式及(9)式求解时,方程组含有j+3个方程,含有2j+2个未知数,当j≥2时,未知数的个数大于方程数,每次计算时需要增加初始条件以满足方程解的唯一性。
当j=1、t0=0、x1(t0)=0、时,可计算出FN,N-1(t0)、及F1,x(t0),在t= Δt时,通过对积分,得到x1(t0+Δt)、,以x1(t0+Δt)、初始条件,求解出FN,N-1(t0+Δt)、及 F1,x(t0+Δt);依次增加时间Δt,反复进行计算滚子1的动力学参数,计算出单向链推送一个节距P的啮合周期Tm内的动力学参数。
当j≥3时,按照上述迭代方法,进行数值仿真,计算每前进位移P的过程中单向链的动力学参数,计算一次完毕,蜗式链盒中减少一链节,下一个链节参与链轮的啮合,单向链伸出部分增加一个链节,弹药前进一个节距P;如此反复,求解出弹药从起始位置到推送到位的整个动力学参数。
4 结果分析
采用上文的仿真方法,借助MATLAB编辑计算程序,将初始条件等主要参数代入到程序中,得到蜗式推送链在推送过程中的动力学响应。推送链机构的主要参数如表1所示,为了便于数值仿真,主要研究水平推送的工况,即K=0,ψ=0°;同时,通过拉力试验[12]测量链节j的刚度系数kj,由于阻尼系数cj难以进行实验测量,采用理论计算的方法获取。

表1 蜗式推送链的主要参数Tab.1 Main parameters of helicoid pushing chain mechanism
在推送开始时,单向链盘曲在蜗式链盒中,由于速度为0,链轮的初始拨动力Fd,0由电机自身特性和启动转矩决定,根据最大启动电流、减速比及链轮的节圆直径,计算出Fd,0=500 N.在速度大于0时,通过(7)式计算电机额定功率Ppo下的驱动力Fd,j+2,当Fd,j+2<Fd,0时,驱动力Fd,j+2由初始设置Fd,0过渡至稳定状态,驱动力由(7)式实时计算得到。同时,将单向链从链盒中抽出的拉力定义为Fp,监测点设置在链盒出口处,抽出力Fp即为监测点处的链节间拉力Fi,i-1.图6为推送过程中抽出力Fp的变化曲线,在运动起始阶段Fp迅速上升,随着时间震荡减小,逐渐趋于0.由于链轮的多边形效应,每抽出一个链节,Fp剧烈波动一次,在整个推送过程中形成众多锯齿状波形曲线。随着链盒中的链节数量逐渐减小,抽出力也逐渐减小,当单向链完全抽出时,Fp趋于0.从曲线可以发现在推送过程中,Fp出现负值,这是受到链轮多边形效应的影响,在一个啮合周期Tm中,单向链的加速度急剧降低,链盒中的链节在自身惯性的作用下对伸出链节产生一定的推力,此时出口处Fi,i-1由拉力变换为压力,造成抽出力Fp短暂出现负值。
图7为链轮对滚子j的拨动力Fd,j(j为1~51),由Fd,j的变化曲线可知:在推送过程中,Fd,j急剧增大,然后震荡减小至近似稳定波动状态,在t为0~0.5 s时,单向链整体处于加速过程,Fd,j陡升之后随着单向链的速度增加而震荡减小,当单向链的速度趋于稳定,Fd,j开始正常波动。在t为0.5~2.1 s时,链轮每经历一个啮合周期Tm,Fd,j震荡一次,且振幅较大,产生较强的啮合冲击,但随着单向链推送距离的增加,Fd,j有减小的趋势。
Corder(1974)将错误分析过程分为五个步骤:(1)收集学习者的语言样本;(2)错误识别;(3)错误描述;(4)错误解释;(5)错误评价。而后,他又将错误分为语言能力错误和语言使用错误两大类,并对错误进行补充,分为前系统性错误、系统性错误和后系统性错误。

图6 抽出力FpFig.6 Pulling force Fp

图7 拨动力Fd,jFig.7 Thrust force Fd,j
为了验证上述仿真结果的正确性,设置了一组推送速度测试试验:将推送链机构安装在测量平台上,平台上放置一定重量的物块,物块与平台间产生的摩擦阻力为200 N,物块在约束的轨道中运动,以模拟弹药的运动过程,且链首仅与物块接触,以保持试验条件与仿真的边界条件一致;间隔200 mm设置测量点,共8个测量点,测试点放置光电开关,当链首经过测量点时,发出速度采集指令,由测速仪X50Ⅱ测量链首速度,如图11所示。
测试并整理采集到的链首速度,与仿真得到推送速度(见图9)进行比较,得到测量速度与仿真速度间的误差,如表2所示。单向链启动时,速度变化较大,且测量值本身存在误差(0.5%),造成测量值与仿真值之间的误差较大;在运动平稳后,能够精确测量出单向链的运动速度,此时仿真值与测量值间的误差较小,因此,建立的动力学模型准确性较高。

图8 滚子i的动力学参数Fig.8 Dynamic parameters of roller i

图9 链首的速度Fig.9 Velocityof chain head
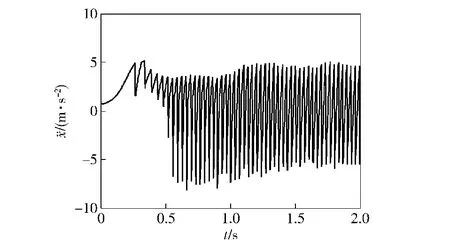
图10 链首的加速度Fig.10 Accelerationof chain head

图11 推送链机构的推送速度测试Fig.11 Pushing velocity test of pushing chain mechanism

表2 速度测量数据表Tab.2 Measurement data
5 结论
1)建立了单向链从链盒中抽出过程及链轮与单向链啮合过程的动力学模型,同时,将单向链伸出部分简化为多弹簧阻尼系统,推导出单向链推送过程的动力学模型,得到了推送链机构的整体动力学模型。
2)采用龙格-库塔法,对推送链整体动力学模型进行了数值仿真,获得蜗式推送链的动力学响应情况。
3)仿真结果表明:在推送过程中,抽出力Fp逐渐震荡减小,最后趋于0,链轮的拨动力Fd,j随时间震荡减小并趋于稳定;由于链轮多边形效应及啮合冲击的影响,链首加速度一直剧烈震动状态,但单向链的链首速度上升至稳定状态后近似恒定,具有较好的推送平稳性,有利于弹药的推送。
4)通过试验测量,得出单向链真实运动速度与仿真速度较为吻合,本文建立的动力学模型准确性较高。
(
)
[1] Lee H J,Park B S,Lee J K,et al.Telescopic tube set for bridge transport system:US,8231096B2[P].2012-07-31.
[2] Enders M L,Green D J.Pyrotechnic safety device with retractable telescoping mechanism:US,7357415B2[P].2008-04-15.
[3] Lee D H,Chang D Y,Shin Y L,et al.Design and application of a wire-driven bidirectional telescopic mechanism for workspace expansion with a focus on shipbuilding tasks[J].Advanced Robotics,2011,25(6/7):699-715.
[4] Zimmer K J,Loomans T J,Lemke L L.Single beam aerial work platform:US,20120024091A1[P].1995-12-19.
[5] Kawabuchi I,Yoon W K,Kotoku T,et al.Linear-motion telescopic mechanism and robot arm having linear-motion telescopic mechanism:US,20120024091A1[P].2012-02-02
[6] 李业农,施祖康.往复推送链负变位设计的研究[J].机械传动,2001,25(4):29-32. LI Ye-nong,SHI Zu-kang.Study on negative designing of reciprocating pushing chain[J].Journal of Mechanical Transmission,2001,25(4):29-32.(in Chinese)
[7] 张丽萍,李业农.往复推送链的运动精度可靠性研究[J].机械科学与技术,2005,24(10):1254-1256. ZHANG Li-ping,LI Ye-nong.Reliability design for displacement accuracy of reciprocating pushing chain[J].Mechanical Science and Technology,2005,24(10):1254-1256.(in Chinese)
[8] Chew M.Inertia effects of a roller-chain on impact intensity[J]. Journal of Mechanisms,Transmissions,and Automation in Design,1985,107:123-130.
[9] Troedsson I,Vedmar L.A method to determine the static load distribution in a chain drive[J].Journal of Mechanical Design,1999,121:402-408.
[10] Troedsson I,Vedmar L.A method to determine the dynamic load distribution in a chain drive[J].Journal of Mechanical Engineering Science,2001,15(5):569-579.
[11] Zheng H,Wang Y Y,Quek K P.A refined numerical simulation on dynamic behavior of roller chain drives[J].Shock and Vibration,2004,11(5):573-584.
[12] Xu L X,Yang Y H,Chang Z Y,et al.Clearance influence on dynamic response of intermittent roller chain drive[J].Chinese Journal of Mechanical Engineering,2010,23(6):699-708.
[13] Xu L X,Yang Y H,Chang Z Y,et al.Dynamic modeling of a roller chain drive system cossidering the flexibility of input shaft[J].Chinese Journal of Mechanical Engineering,2010,23(2): 1-8.
[14] Spicer J B.Effects of the nonlinear elastic behavior of bicycle chain on transmission efficiency[J].Journal of Applied Mechanics,2013,80(2):599-605.
Dynamics Analysis of Helicoid Pushing Chain Mechanism for Automatic Ammunition Loading System
ZHANG Lei-yu,YANG Yang
(School of Mechanical Engineering and Automation,Beihang University,Beijing 100191,China)
The helicoid pushing chain mechanism is a novel telescopic mechanism used to push objects from one position to another one rapidly.It occupies a minimal amount of space in the contact status.In constrained space the helicoid chain case adopted may store as many links as possible for acquiring a long telescopic distance.In order to analyze the influences of polygon effect and meshing impact on the dynamic properties and pushing stability of the unidirectional chain,the dynamics models are established for the processes of extracting the unidirectional chain from the helicoid chain case and it meshing with the sprocket.Meanwhile,the extended part is simplified as a multi-spring-damping system,and the dynamics model of pushing process is deduced.The full dynamics models is numerically simulated by using MATLAB software and Rung-Kutta method.The simulation results show that the drawing force acted on the unidirectional chain in the chaincase drops down to zero concussively over time,and the change of the thrust force transits form drastic oscillation to smooth fluctuation.Besides,the pushing velocity of the chain is nearly constant during the pushing process.Hence this mechanism has an excellent pushing sta-bility.In addition,the established dynamics models are verified by the experimental measurement of the pushing velocity.
ordnance science and technology;pushing chain mechanism;linear telescopic mechanism;polygon effect;unidirectional chain;multi-spring-damping system
TH122
A
1000-1093(2015)11-2024-08
10.3969/j.issn.1000-1093.2015.11.002
2014-11-03
总装备部预先研究项目(41462030101RD01)
张雷雨(1988—),男,博士研究生。E-mail:zhangleiyu1988@126.com;杨洋(1962—),男,教授,博士生导师。E-mail:yang_mech@buaa.edu.cn

