基于计算流体力学与质点弹道耦合的底部排气弹工作过程以及射程预示

卓长飞，姚文进，武晓松，徐文科，封锋

（1.南京理工大学机械工程学院，江苏南京210094；2.辽沈工业集团有限公司，辽宁沈阳110045）

基于计算流体力学与质点弹道耦合的底部排气弹工作过程以及射程预示

卓长飞1，姚文进1，武晓松1，徐文科2，封锋1

（1.南京理工大学机械工程学院，江苏南京210094；2.辽沈工业集团有限公司，辽宁沈阳110045）

基于计算流体力学的优点以及目前底部排气弹射程预示问题，采用计算空气动力学和质点外弹道学耦合的方法求解底部排气弹的飞行弹道，获得在整个减阻阶段底部排气弹底排装置工作参数、工作状态、底排流场等随时间的变化规律。研究结果表明：不同海拔发射的底部排气弹在减阻阶段的排气参数均随着时间的增加而呈增大的趋势，但在减阻末阶段，变化趋势变缓；随着海拔高度的增加，阻力系数随时间的增大而增加的趋势变得平缓，甚至会出现下降的趋势；在海拔0 km发射的底部排气弹在减阻阶段前期，底排装置以底排减阻模式工作，到减阻阶段中后期，底排装置的工作模式介于底排减阻模式和火箭增程模式之间。

兵器科学与技术；计算流体力学；底部排气弹；质点弹道；射程

0 引言

底部排气弹（以下简称底排弹）减阻增程的原理［1］是在常规炮弹底部附加一个排气装置，向底部低压区排入低动量高温气体，改变底部低压区的流动状态，达到提高底部压力、减小阻力、增大射程的目的。国内在20世纪90年代对底排增程技术进行了大量研究，取得了突出的成绩，为国内底排增程技术的发展奠定了基础。此后，国内底排增程技术的研究基本处于停滞状态。目前，国内底排增程弹在使用过程中暴露出许多问题，比如底排药柱燃烧稳定性较差、底排药柱完整性较差、增程率低问题。因此，深入研究底排增程技术与底部排气弹相关问题是很有必要的。

由于底排装置出口不带有拉瓦尔喷管，底排装置内底排药柱燃烧产生的高温燃气理论上都应该以亚声速排到弹丸底部低压区。因此，底排药柱燃烧受环境影响因素较大，特别是随着环境压力的降低，底排药柱的燃速也随着降低。这与火箭发动机燃烧有较大区别，火箭发动机有拉瓦尔喷管，燃气以超声速喷出，环境压力不能影响火箭发动机内药柱的燃速。此外，底排药柱属于贫氧推进剂，燃烧后产生大量的CO和H2，这部分富燃气体排到弹丸底部与来流空气进一步发生二次燃烧，继续放热，有利于提高底部压力。显然，来流空气的温度与压力影响着富燃气体的二次燃烧，从而影响底部流场压力和全弹气动力。由此可以看出，底排弹底排装置的工作以及气动力受环境影响较大，底排弹的气动力和射程较难预估，特别是在不同海拔高度使用底排弹时，其射程、增程率以及底排弹的真实工作情况基本处于未知状态。目前，底排弹的气动数据十分缺乏，并没有统一的标准气动力数据。射程预估是靠靶场试验反推气动力数据和弹形系数，得到的弹形系数也是全弹道平均值。采用该平均弹形系数计算底排弹的弹道仅能预估其射程，不能预估详细的飞行轨迹。此外，由于底排弹受环境因素影响较大，采用靶场试验得到的气动力数据和平均弹形系数计算不同海拔高度使用底排弹的弹道有较大的误差。

20世纪80年代以来，随着计算流体力学（CFD）方面的长足进步和计算机技术的迅速发展，使得CFD在常规兵器的气动与流场研究方面几乎起到了和地面试验、飞行试验并重的作用。CFD可以提供试验无法提供的复杂流动现象的流动细节，得到飞行器的各种气动力参数，为深刻了解复杂流动的物理本质提供丰富的数据，进而对飞行器进行优化设计，以达到最佳飞行特性。

国内外对底部排气减阻进行了相关试验与数值研究。丁则胜等［2-3］开展大量底排冷气或热空气风洞试验。卓长飞等［4-5］开展了在底排真实燃气条件下的减阻流场与特性、来流攻角和弹体船尾角对减阻的影响以及在排气结构对减阻性能的影响研究。Mathur等［6-7］开展了底排冷空气的风洞试验，并得到详细的流场参数。Nietubica等［8］采用层流流动模型和层流燃烧有限速率基元反应模型模拟了M864弹的二维轴对称流场。Kaurinkoski［9］采用k-ε湍流流动模型和层流燃烧有限速率基元反应模型模拟了155 mm弹的三维流场。Choi［10］采用k-ω湍流流动模型与层流燃烧有限速率基元反应模型模拟了155 mm弹的二维轴对称流场。这些研究都是以底排减阻机理与特性为研究对象，并没有完全结合工程中的底排弹开展研究，特别是底部排气弹在整个减阻飞行阶段中底排装置工作状态、底部排气流场结构、减阻效果随时间的变化研究基本处于空白。

基于CFD的优点以及目前底排弹射程预示问题，本文在前期编写的CFD程序上添加底排弹的质点外弹道模型，建立了基于CFD耦合质点弹道的底排弹工作过程的计算模型，复现在整个减阻阶段底排弹底排装置工作参数、工作状态、底排流场等随时间的变化。同时，研究在不同海拔高度下使用底排弹时的底排弹工作状态以及射程，为底排弹的优化设计和底排弹射程标准化研究提供了重要参考。

1 数学与物理模型

1.1 CFD基本控制方程

底排弹是高速旋转飞行的，旋转将影响底排药柱的燃速以及全弹流场与气动。但是由于本文与质点外弹道耦合计算，计算量较大，不可能实时计算底排弹的三维流场。因此，和文献［8-10］的假设一样，本文不考虑飞行攻角，采用二维轴对称模型计算底排弹流场与气动力。在小攻角下（0°～5°），这样计算得到的流场、气动差别与真实三维旋转情况下的气动力基本无差别。二维轴对称守恒形式的雷诺时均（RANS）化学非平衡流Navier-Stokes方程［11］为

式中:U为守恒变量；F、G为两个方向无粘对流通量；Fv、Gv为两个方向粘性通量；H为轴对称源项；Srec为化学反应源项。各符号详细意义见文献［11］.

超声速底部流动中湍流流动特性较强，本文选用在分离流动中模拟性能较好的k-ω SST两方程湍流模型［12］，它是一种在工程上得到广泛应用的混合湍流模型。

1.2 化学反应动力学模型与湍流燃烧模型

底排弹燃烧产物主要是由CO、H2、CO2、H2O、 N2等组成，因此采用CO-H2-O2化学反应系统。本文采用8组分（CO、H2、O2、CO2、H2O、H、OH、O）12个基元反应的CO-H2-O2系统化学反应模型［9］，基元反应表达式和系数如表1所示。考虑到超声速底部流场具有较强湍流特性，本文选择2阶矩湍流燃烧模型控制湍流-化学反应相互作用机理［13］。

表1 CO-H2-O2基元反应模型Tab.1 Detailed reaction model of CO-H2-O2

1.3 CFD计算格式与计算方法

为了很好地捕捉激波、膨胀波等流场细节，空间离散采用3阶MUSCL重构方法和高精度高分辨率的AUSMPW+迎风通量分裂格式［14］，粘性项采用中心格式离散，时间离散采用单步推进，并采用局部时间步长法加速收敛。湍流两方程与时均Navier-Stokes方程形式一致，与之耦合求解。

本文CFD数值方法的详细描述及其数值验证见文献［4-5］，这里不再赘述。

1.4 质点弹道模型

质点弹道模型主要假设弹丸在飞行期间的攻角为0，以及弹丸为轴对称体，使空气阻力和重力作用在弹丸的质心上。因此可以把弹丸的运动作为质点运动处理。

底排弹质心运动方程如下:

式中:Sref为弹体参考面积；ρ为来流气体密度；v为弹丸飞行速度；m为弹丸质量；g为重力加速度；θ为弹道倾角；Cd为弹丸阻力系数，其值由CFD方法计算得到。上述常微分方程组采用4阶龙格-库塔法求解，推进时间步长为0.001 s.

由于CFD计算量较大，不可能采用CFD实时计算流场，为质点弹道方程组提供阻力系数。本文采用松耦合的方法处理CFD和质点弹道方程组的求解，即质点弹道方程推进k步后，然后采用CFD计算底排弹阻力系数。如此反复计算，直到底排弹落到地面为止。由于质点弹道方程组推进时间步长为0.001 s，因此可取k=500，即底排弹每运动0.5 s后就采用CFD计算此位置处底排弹全弹流场与总阻力系数。由于底排弹在每个0.5 s时间段内飞行速度、环境压力、环境密度变化并不大，可认为在这时间段内阻力系数为常数。因此，本文这种松耦合处理方法是合理的。

1.5 物理模型

本文以某底排弹为研究对象，弹丸计算网格如图1所示。由于计算域为二维轴对称模型，只需计算上半平面的流场。为了方便观察，下半平面的流场数据根据对称性得出。在飞行过程中，底排药柱燃烧面积和底排装置燃烧室内体积在不断变化，且药柱形状复杂，不能简化为二维轴对称模型。因此，本文将燃烧室计算域固定，并假定一个面为药柱燃烧表面，在飞行中与燃面变化规律、流场计算耦合得到的药柱燃烧质量流率即施加在该假定的燃烧表面上。

图1 底排弹计算网格Fig.1 The computational grid of base bleed projectile

弹丸基本参数:弹丸发射前总质量为31.8 kg，底排喷口直径为42 mm，发射初速947 m/s.

底排药柱基本参数:底排药柱为三瓣药结构（药柱横截面如图2所示），两端与外侧面包覆，底排药柱质量为0.9 kg，药柱外径2r2=100 mm，内径2r1=44 mm，药柱长度L=97 mm，狭缝宽2c1= 2 mm，药柱密度ρs为1 520 kg/m3，药柱燃烧温度为1 812 K，燃烧规律服从几何燃烧规律。燃面变化规律为

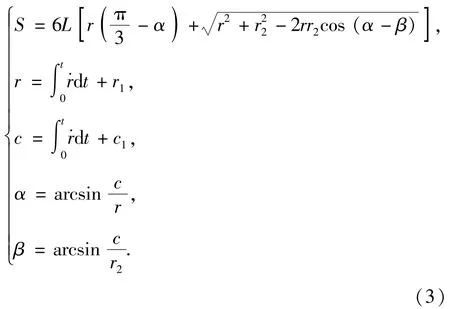
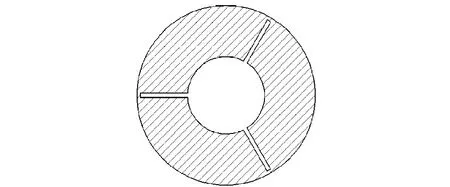
图2 底排药柱横截面Fig.2 The cross section of base bleed propellant

底排药柱燃速公式:

式中:S为燃烧面积；燃速系数ε为因弹丸旋转引起的燃速修正系数，取1.3；燃速系数a为4.903× 10-6m/s；p为燃烧室燃气压强（Pa）；n为底排药柱燃烧压强指数，取0.484.

由燃烧面积、燃速、药柱密度即可得到底排燃气生成质量流率，即可作为CFD中燃面边界条件，但是药柱燃速又与流场压力有关，即施加在燃面边界上的燃气生成质量流率:

该质量流率又会在CFD计算中影响燃烧室压力。因此，在某一时刻的流场计算中，CFD流场计算与底排燃气生成率需要相互耦合求解，直到流场达到稳定为止。

为了研究在不同海拔高度下使用底排弹的工作状态以及射程，本文计算了如表2所示的工况。

表2 计算工况Tab.2 Calculation cases

在外弹道计算中，气象模型的选择将决定外弹道计算的精度。因此，在分析弹道数据时必须选取统一标准气象模型。本文基本的气象模型选用我国炮兵标准气象模型［1］。地面标准值:地面海拔，气温T0=15℃，气压p0=99.992 7 kPa.

2 计算结果与分析

表3给出了不同海拔高度处发射底排弹的底排药柱燃烧时间、飞行时间、射程和增程率。同时，表3中也给出了和底排弹具有相同质量、相同外形、无底排装置的常规炮弹的相关飞行参数，以便和底排弹作对比。从表3中可看出，随着发射处海拔高度的增加，底排装置内底排药柱燃烧时间也将增大。在高海拔处发射底排弹时，其周围环境压力较低，且整个飞行弹道过程中底排弹所处的平均环境压力低于低海拔处发射的底排弹。由于底排弹整个飞行过程中环境压力较低，对应的底排装置内燃气压力也较低。因此，高海拔处发射的底排弹整个飞行过程中底排药柱平均燃速较低，在相同质量和相同形状的药柱下，其燃烧时间显然更长。

从表3中看出，无底排装置的常规炮弹和含有底排装置的底排弹都会随着发射处海拔高度的增加，整个飞行时间和射程也会增加。在高海拔处发射的常规炮弹和底排弹，整个飞行弹道过程中所处的空气密度更稀薄，阻力更小，因而其飞行时间和射程都相比于在低海拔处发射时有所增加。此外，对于底排弹来说，由于在高海拔处发射时底排药柱燃烧时间较长，减阻时间有所增加，对射程的增加也有一定贡献。

增程率δ的计算公式如下:

式中:xBB为底排弹的射程；xNB为无底排装置的常规炮弹射程。

从表3中还可以看出，不同海拔处发射的底排弹相比于无底排装置的常规炮弹的增程基本维持在9 km左右，而对应的无底排装置的常规炮弹随着发射海拔高度的增加而增加。因此，随着发射海拔高度的增加，增程率逐渐降低。

表3 不同海拔高度处发射底排弹的工作参数Tab.3 The operating parameters of base bleed projectiles launching at different altitudes

图3给出了不同海拔高度处发射无底排的炮弹和底排弹的飞行弹道。为了方便对比，所有飞行弹道的坐标原点均为所处的发射位置。可以明显看出，在初始阶段，不同海拔高度发射的无底排装置的常规炮弹和有底排装置的底排弹飞行弹道基本重合，特别是在水平位移10 km以内，几乎不能发现所有的弹道有区别。水平位移10 km以后，所有弹道开始出现明显的差异。图4、图5给出了底排弹飞行水平位移和垂直位移随时间的变化。在0～10 s以内，水平位移和垂直位移基本完全重合。这是由于在此阶段，不同海拔发射的底排弹的阻力系数差别较小，且此阶段时间短，不能明显发现飞行速度的差异。因此导致水平位移和垂直位移基本完全重合。20 s以后，不同海拔发射的底排弹的水平位移和垂直位移随时间的变化有明显的差异。且随时间的增加，差异也明显增加。这是因为不同海拔发射的底排弹的阻力系数有差异，来流空气密度也有差异，随着时间的积累，最终导致飞行速度以及飞行弹道有差异。

图3 无底排炮弹和底排弹的飞行弹道Fig.3 The flight trajectories of projectiles with and without base bleed

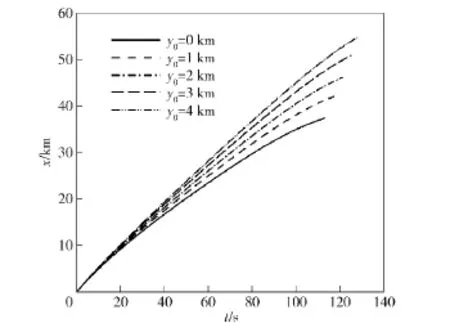
图4 底排弹飞行水平位移x随时间t的变化Fig.4 Horizontal displacement of base bleed projectile vs.time

图5 底排弹飞行垂直位移y随时间的变化Fig.5 Vertical displacement of base bleed projectile vs.time

图6给出了不同海拔处发射的底排弹全弹道飞行马赫数随时间的变化。从变化曲线可以看出，在任意时刻下，高海拔发射的底排弹对应的的飞行马赫数始终大于低海拔发射的底排弹。以t=0 s为例，即处于发射位置处，高海拔发射位置对应的环境温度较低，声速较低。因此，在相同发射初速的情况下，该时刻的飞行马赫数较高。对于其他时刻，由于高海拔发射的底排弹飞行阻力较小，飞行存速较大，同时由于对应的环境温度和声速低。因此，其他时刻高海拔发射的底排弹对应的的飞行马赫数同样大于低海拔发射的底排弹。另外，从马赫数随时间变化曲线看出，在底排弹下降阶段总会出现一个马赫数的极值。从标准气象数据可得到，在海拔10 km以上，气温基本都保持221.65 K不变，即声速保持不变。因此，底排弹达到最高点后下降前期（海拔10 km以上），速度逐渐增大，但声速基本保持不变，因此马赫数逐渐增大。然而，在下降到10 km以下，大气温度逐渐增大，声速也逐渐增大。虽然速度也逐渐增大，但速度增大率始终小于声速的增大率。因此，导致马赫数逐渐降低，即在下降阶段达到海拔10 km时马赫数出现极值。对于其他海拔高度发射的底排弹，都会在下降阶段达到海拔10 km时马赫数出现极值。

图7给出了不同海拔处发射的底排弹在减阻阶段燃烧室平均压力随时间的变化。由于底排装置内底排燃气流动速度非常低，燃烧室内空间各处燃气压力基本一致。从（4）式可知，燃烧室内平均压力直接影响底排药柱的燃速以及底排燃气生成质量流率，从而影响减阻和全弹总阻力系数。

图6 底排弹飞行马赫数随时间的变化Fig.6 Mach number of base bleed projectile vs.time

图7 减阻阶段燃烧室平均压力随时间的变化关系Fig.7 Average pressure of combustion chamber vs. time in drag reduction stage

图8、图9分别给出了不同海拔处发射的底排弹在减阻阶段排气质量流率、排气参数I随时间的变化。排气参数I是底排装置排气质量流率与炮弹迎面空气质量排开率之比，数学定义式为

式中:ρinf表示来流密度；uinf表示来流速度。

排气参数I直接影响排气减阻效果，是十分重要的参数。卓长飞等［4］深入开展了排气参数与减阻效果的关系研究。这里仅简单叙述一下排气参数与减阻效果的关系:在排气参数较小时，底压比随排气参数I的增大而增大（底部阻力系数、全弹总阻力系数随排气参数I的增大而减小），这一阶段为底部排气减阻区；当排气参数超过一定值后，底压比随着排气参数I的增大而减小（底部阻力系数、全弹总阻力系数随排气参数I的增大而增大），这一阶段介于底排减阻和火箭增程区之间；当排气参数较大时，底压比随排气参数I的增大而增大（底部阻力系数、全弹总阻力系数随排气参数I的增大而减小），这一阶段，由于排气质量流率和排气速度较大，成为火箭发动机增速原理，而不是底排减阻原理，因此称为火箭增程区。不同的弹丸、底排装置和飞行状态，底压比、阻力系数与排气参数的具体变化规律有所不同，但变化趋势却是一致的。从图9中看出，不同海拔处发射的底排弹在减阻阶段的排气参数均随时间的增加而呈增加趋势。这是由于在减阻阶段，随着时间的增加，底排燃气排气质量流率逐渐降低，而炮弹迎面空气质量流率也逐渐降低（在减阻阶段，弹丸飞行高度一直上升，弹丸速度、来流空气密度均降低），但迎面空气质量流率下降程度更剧烈。因此，不同海拔发射的底排弹在减阻阶段的排气参数均随着时间的增加而呈增大的趋势。但在减阻末阶段，排气参数随时间的增加而变化较为缓慢。特别是对于在海拔0 km发射的底排弹，在时间t=20 s之后，排气参数略有下降的趋势，说明在此阶段底排燃气排气质量流率下降程度大于炮弹迎面空气质量流率下降的趋势。从数值上比较可以发现，在任意时刻，随着发射位置海拔高度的增加，排气参数也将增加。这仍然可以从排气参数的定义来解释:以初始时刻为例，对于在海拔4 km发射的底排弹，由于在初始时刻所处位置的空气密度较0 km处发射的底排弹更稀薄，即炮弹迎面空气质量流率较小。虽然从底排燃气排气质量流率来看，在初始时刻0 km发射的底排弹的排气质量流率大于4 km发射的底排弹，但因迎面空气质量流率更低。因此，最终表现为4 km发射的底排弹的排气参数大于0 km发射的底排弹。

图10给出了不同海拔处发射的底排弹底排药柱燃烧面积随时间的变化。由于底排药柱形状是固定的，初始燃烧面积和终止燃烧面积也都是固定的，具体燃烧面积随时间的变化规律由燃速决定。从前面分析可知，低海拔发射的底排弹底排药柱平均燃速较高，燃烧时间较短，因此，低海拔发射的底排弹底排药柱燃烧面积随时间的变化更陡峭，即变化斜率更大于高海拔发射的底排弹。

图8 减阻阶段排气质量流率随时间的变化关系Fig.8 Mass flow rate of base bleed vs.time in drag reduction stage

图9 减阻阶段排气参数I随时间的变化关系Fig.9 Parameter I of base bleed vs.time in drag reduction stage

图10 底排弹药柱燃烧面积随时间的变化关系Fig.10 Combustion area of propellant of base bleed projectile vs.time

图11给出了不同海拔处发射的底排弹在减阻阶段全弹总阻力系数随时间的变化。根据弹箭空气动力学理论，当为超声速飞行时，全弹阻力系数随飞行马赫数的增加而降低。结合图6可以看出，在减阻阶段，不同海拔发射的底排弹飞行马赫数均随时间的增大而逐渐降低。如果无底排减阻作用，全弹阻力系数会随着时间的增大而增大。但是从阻力系数曲线看出，只有在0 km发射的底排弹的阻力系数会随着时间的增大而呈增加趋势，其余海拔高度发射的底排弹阻力系数随时间变化平缓。特别是在4 km海拔高度发射的底排弹阻力系数在减阻阶段后期会随着时间的增加而逐渐降低，说明了此时底排燃气作用较大，让本身应该增大的阻力系数降低。在此阶段，排气参数较大，底排装置工作状态以及底部流场结构必须通过流场分析获得。

图11 减阻阶段阻力系数Cd随时间的变化关系Fig.11 The variation of drag coefficient Cdat reduction stage with time

图12 海拔0 km处发射的底排弹在主要时刻底部流场马赫数云图和流线Fig.12 The contours of Mach number and streamline on the bottom of the base bleed projectile launching at altitude of 0 km

图12～图14给出了海拔0 km处发射的底排弹在飞行中底部流场云图。由于篇幅有限，本文仅给出3个时刻的流场云图:0 s、10 s、20 s.在t=0 s，排气参数较小，约为0.004 5，底排燃气射流动量也较小，底排燃气不仅在尾流场中心轴线上与来流空气形成主回流区，而且还在弹底附近与来流空气形成二次回流区。通过前期研究可以断定，此时底排装置正在以底排减阻模式工作，处于最佳减阻状态附近。从温度和CO2质量分数云图可以看出，CO2主要在主回流区内以及自由来流边界层附近生成。主回流区是由底排燃气和来流空气共同形成，里面含有底排燃气CO和来流空气中的O2，两种气体在主回流区内搅拌混合并发生化学反应生成CO2.自由来流边界层是自由来流空气与底排燃气的主要分界面，底排燃气中部分CO和来流O2接触，发生化学反应生成CO2.由于整个底部流场是处于低温、低压的来流空气中，化学反应并不能大幅度提高燃烧温度，这不同于火箭发动机内高温高压气体燃烧，可以发现一个重要的特点，底部排气流场中CO化学反应较为活跃，但是对燃烧温度并没有太大的提高。从温度云图还可以看出，靠近弹底附近的自由边界层温度略有一定的升高。从t=10 s时刻云图和流线看出，此时排气参数I和排气动量较大，底排燃气直接以射流形式进入尾流中，并未与来流空气在轴线上形成主回流区。但此时底排出口马赫数并没达到1.0，即底排装置内没有达到气体壅塞状态，整个底排流场处于底排减阻模式和火箭增程模式之间工作。可以断定此时减阻效果是较差的，并没有处于减阻最佳状态。从温度和CO2质量分数云图可以看出，由于主回流区的消失，CO2主要集中在二次回流区以及自由来流边界层附近生成。此刻，流场中最大温度低于t=0 s时刻。在t=20 s时刻，流场结构与t=10 s时基本一致，但此时底排燃气射流动量更大，底排喷口马赫数相对于t=10 s时刻有所增大，但仍然小于1，即处于底排减阻模式和火箭增程模式之间工作，减阻效果仍然没有达到最佳。从温度和CO2质量分数看出，二次回流区内CO2含量明显大于t=0 s和t=10 s时刻，尾流场高温“火舌”长度有所增长。

图13 海拔0 km处发射的底排弹在主要时刻底部流场温度云图Fig.13 The contours of temperature on the bottom of the base bleed projectile launching at altitude of 0 km

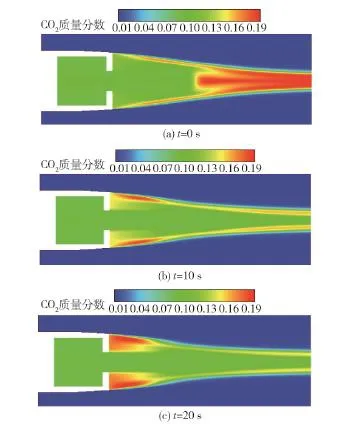
图14 海拔0 km处发射的底排弹在主要时刻底部流场CO2质量分数云图Fig.14 The contours of CO2mass fraction on the bottom of the base bleed projectile launching at altitude of 0 km

图15 海拔4 km处发射的底排弹在主要时刻底部流场马赫数云图和流线Fig.15 The contours of Mach number and streamline on the bottom of the base bleed projectile launching at altitude of 4 km

图15～图17给出了海拔4 km处发射的底排弹在飞行中主要时刻底部流场云图。在t=0 s，排气参数为0.006，底排燃气射流动量较大，底排燃气直接冲破主回流区进入尾流中。在t=10 s时刻，排气参数达到0.01，底排喷口燃气马赫数已经达到1以上，底排燃气以超音速喷出并在喷出后形成相交激波、反射激波、激波串等复杂的波系。在t=20 s时刻，排气参数达到0.013，底排喷口燃气马赫数更高，相交激波强度更强。可以断定，对于海拔4 km发射的底排弹，在飞行至少10 s以后，底排装置均是以火箭增程模式工作，且随着时间的增加，底排喷口马赫数逐渐增大。结合图11的阻力系数曲线看出，10 s以后，底排装置处于火箭增程模式工作，导致全弹总阻力系数逐渐缓慢下降。需要说明的是，在t=20 s时刻，采用CFD计算得到的流场不稳定，尾流出现微弱的波动，这可以从CO2质量分数云图和温度云图看到局部区域相比于其他时刻有“皱褶”，这是流场不稳定的表现。这可能是由于底排燃气射流速度较大，与外流空气相互更加复杂，造成流动失稳。

图16 海拔4 km处发射的底排弹在主要时刻底部流场温度云图Fig.16 The contours of temperature on the bottom of the base bleed projectile launching at altitude of 4 km

3 结论

本文利用前期发展的基于多块结构网格的二维/三维化学反应流CFD求解程序，耦合底部排气弹质点外弹道方程，建立了基于CFD耦合质点弹道的底部排气弹工作过程的计算模型，分析了不同海拔高度发射的底排弹的工作过程和射程，得到以下重要结论:

1）不同海拔发射的底排弹在减阻阶段的排气参数均随着时间的增加而呈增大的趋势。但在减阻末阶段，排气参数随时间的增加而变化较为缓慢。特别是对于在海拔0 km发射的底排弹，在时间t= 20 s之后，排气参数略有下降的趋势。

2）从阻力系数曲线看出，在0 km发射的底排弹的阻力系数随着时间的增大而呈增加趋势，其余海拔高度发射的底排弹阻力系数随时间变化平缓。特别是在4 km海拔高度发射的底排弹阻力系数在减阻阶段后期会随着时间的增加而逐渐降低。

图17 海拔4 km处发射的底排弹在主要时刻底部流场CO2质量分数云图Fig.17 The contours of CO2mass fraction on the bottom of the base bleed projectile launching at altitude of 4 km

3）从主要时刻流场云图看出，在0 km发射的底排弹减阻前期，底排装置以底排减阻模式工作。到减阻阶段中后期，底排装置的工作模式介于底排减阻模式和火箭增程模式之间。在4 km发射的底排弹减阻前期，底排装置的工作模式介于底排减阻模式和火箭增程模式之间。到减阻阶段中后期，底排装置的工作模式为火箭增程模式。

通过本文的研究发现，目前该底排弹的排气参数较大，大部分减阻阶段均不在最佳底排减阻模式下工作。因此，建议重新设计底排药柱燃面，使得在任意时刻，底排燃气生成质量流率与弹丸迎面空气质量流率的比值合理，以保证底排弹的减阻性能达到最优。

（

）

［1］ 郭锡福.底部排气弹外弹道学［M］.北京:国防工业出版社，1994. GUO Xi-fu.The exterior ballistics of base bleed projectile［M］. Beijing:National Defense Industry Press，1994.（in Chinese）

［2］ 丁则胜，陈少松，刘亚飞，等.底排尾迹流场实验研究［J］.弹道学报，2000，12（1）:43-47.DING Ze-sheng CHEN Shao-song，LIU Ya-fei，et al.A study of wake flow field of base bleed［J］.Journal of Ballistics，2000，12（1）:43-47.（in Chinese）

［3］ 丁则胜，陈少松，刘亚飞，等.底排性能的环境压力效应［J］.弹道学报，2002，14（1）:88-92. DING Ze-sheng，CHEN Shao-song，LIU Ya-fei，et al.Influence of ambient pressure on base bleed［J］.Journal of Ballistics，2002，14（1）:88-92.（in Chinese）

［4］ 卓长飞，武晓松，封锋.超声速流动中底部排气减阻的数值研究［J］.兵工学报，2014，35（1）:18-26. ZHUO Chang-fei，WU Xiao-song，FENG Feng.Numerical research on drag reduction of base bleed in supersonic flow［J］.Acta armamentarii，2014.35（1）:18-26.（in Chinese）

［5］ 卓长飞，武晓松，封锋.超声速流动中底部排气形式对减阻性能的影响［J］.航空学报，2014，35（8）:2144-2155. ZHUO Chang-fei，WU Xiao-song，FENG Feng.Effect of base bleed type on drag reduction performance in supersonic flow［J］. Acta Aeronautica et Astronautica Sinica，2014，35（8）:2144-2155.（in Chinese）

［6］ Mathur T，Dutton J C.Base bleed experiments with a cylindrical afterbody in supersonic flow［J］.Journal of Spacecraft and Rockets，1996，33（1）:30-37.

［7］ Mathur T，Dutton J C.Velocity and turbulence measurements in a supersonic base flow with mass bleed［J］.AIAA Journal，1996， 34（6）:1153-1159.

［8］ Nietubica C J，Gibeling H J.Navier-stokes computations for a reacting，M864 base bleed projectile，AIAA 93-0504［R］.US: AIAA，1993.

［9］ Kaurinkoski P.Computation of the flow of thermally perfect gas past a supersonic projectile with base bleed［C］∥AIAA AFM Conference.San Diego，CA，US:AIAA，1996:725-734.

［10］ Choi J Y.Numerical study of base bleed projectile with external combustion，AIAA 2005-4352［R］.US:AIAA，2005:10-13.

［11］ 欧阳水吾，谢中强，徐春光.高温非平衡空气绕流［M］.北京:国防工业出版社，2001:140-142. OUYANG Shui-wu，XIE Zhong-qiang，XU Chun-guang.High temperature air non-equilibrium flows［M］.Beijng:National Defense Industry Press，2001:140-142.（in Chinese）

［12］ Menter F R.Two equation eddy viscosity turbulence models for engineering application［J］.AIAA Journal，1994，32（8）:1598-1605.

［13］ 周力行.多相湍流反应流体力学［M］.北京:国防工业出版社，2002. ZHOU Li-xing.Multiphase turbulent reaction fluid dynamics［M］. Beijng:National Defense Industry Press，2002.（in Chinese）

［14］ Kim K H.Accurate computation of hypersonic flows using AUSMPW+scheme and shock-induced grid technique，AIAA-98-2442［R］.US:AIAA，1998.

Research on Operation Process and Firing Range of Base Bleed Projectile Based on Computational Fluid Dynamics Coupled with Particle Trajectory

ZHUO Chang-fei1，YAO Wen-jin1，WU Xiao-song1，XU Wen-ke2，FENG Feng1
（School of Mechanical Engineering，Nanjing University of Science and Technology，Nanjing 210094，Jiangsu，China；Liaoshen Industries Group Co.，Ltd，Shenyang 110045，Liaoning，China）

Based on the advantages of computational fluid dynamics and the firing range prediction of base bleed projectile，the flight ballistic trajectory of base bleed projectile is solved by using the computational aerodynamics coupled with particle trajectory，and the change laws of operating parameter，operating state，and flow filed of base bleed projectile with time are obtained.The results show that the base bleed parameters of the base bleed projectiles launched at different altitudes increase with the increase in time in early drag reduction stage，but it varies slowly with the increase in time in the late drag reduction stage；with the increase in altitude for launching，the drag coefficient of the base bleed projectile increases slowly with the increase in time in the drag reduction stage，and even it decreases with the time.For the base bleed projectile launching at altitude of 0 km，the base bleed device in the early drag reduction stage operates in the mode of base bleed.And in the late stage，the base bleed device operates between base bleed mode and rocket mode.

ordnance science and technology；computational fluid dynamics；base bleed projectile；particle trajectory；firing range

V211.3

A

1000-1093（2015）11-2062-11

10.3969/j.issn.1000-1093.2015.11.007

2015-04-10

国家自然科学基金项目（11402119）；中央高校基本科研业务费专项资金项目（30915118811）；江苏省研究生科研创新计划项目（CXLX13-202）

卓长飞（1987—），男，博士研究生。E-mail:njust203zcf@126.com；武晓松（1960—），男，教授，博士生导师。E-mail:nust203@mail.njust.edu.cn