炮钢材料动态本构模型及其验证

曾志银，高小科，刘朋科，喻华萨

（西北机电工程研究所，陕西咸阳712099）

炮钢材料动态本构模型及其验证

曾志银，高小科，刘朋科，喻华萨

（西北机电工程研究所，陕西咸阳712099）

在温度88～573 K和应变率0.001～2 000 s-1的条件下，通过温度与应变率耦合的静态和动态分离式Hopkinson压杆实验，并以初步获得的炮钢材料动态本构模型基本参数为基础，通过进一步的优化及Taylor杆冲击实验，验证并最终确认了炮钢材料动态本构模型参数，模型预测与实验结果相对误差小于5%.验证结果表明，建立的炮钢材料动态本构模型能真实地反映其动态响应。

兵器科学与技术；炮钢材料；本构模型；Hopkinson压杆实验；Taylor杆冲击实验

0 引言

炮钢是火炮主要承力构件最常使用的一种材料，如身管、炮尾、闩体等。炮钢材料的本构模型尤其是动态本构模型更是现代火炮结构动态强度设计必须考虑的主要因素之一。

材料本构模型是描述材料总的力学行为的一种表征形式。本构模型通常用一个或一组方程表示，这些方程将应变率与应力、应力的变化率、温度、材料的热力学历史等相联系。针对金属经受动态载荷、大应变、高应变率和高温，Johnson和Cook提出了一个本构模型（简称J-C模型）［1］如下:

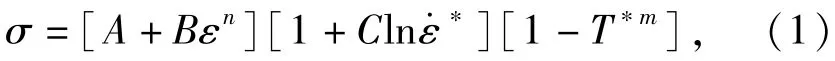
式中:A是Von Mises流动应力；ε是等效塑性应变；B为材料应变硬化模量；C为应变率效应系数；m为温度效应系数；n为应变硬化指数；是在取1.0 s-1下无量纲化的塑性应变率；T*是相应的温度，其形式如下:

式中:Tr是参考温度，可取室温；Tm是材料的熔点温度。J-C模型由于形式简单且有多种材料的J-C模型参数已被获得，所以此模型已得到了广泛而成功地运用。

国内外对金属材料的本构模型进行了大量研究，如文献［2］对AF1410钢在温度从100 K到600 K，应变率从0.001 s-1到2000 s-1的塑性流动特性进行了研究，建立了AF1410钢的塑性流动物理概念本构模型。文献［3］基于静力、扭转及Hopkinson拉杆实验结果，修改了J-C模型中的应变强化项以及J-C失效模型中的温度软化项，并结合数值仿真得到了模型参数，通过对较高速度下Taylor撞击实验的模拟，比较撞击后弹体变形与破坏形式，验证了模型及参数的有效性和可靠性。文献［4］通过采用约束条件下的多变量非线性规划方法，结合有关流应力实验数据确定出了多晶钽的动态本构模型。文献［5］采用电子万能试验机和高温分离式Hopkinson压杆（SHPB）分别对Fe-36Ni因瓦合金进行准静态实验和动态压缩实验，得到其高温、高应变率下的应力-应变曲线，采用改进应变率项和温度项的J-C本构方程拟合了Fe-36Ni因瓦合金在高温、高应变率下的动态塑性本构模型。文献［6］应用人工神经网络算法，预测高强度装甲钢在高应变率下的流动应力，并与J-C模型进行了对比。

虽然国内外对金属材料的本构模型进行了广泛的研究，但有关炮钢材料的本构模型研究鲜有报道，本文基于高温、高应变率耦合的SHPB实验，初步获得炮钢材料动态本构模型参数，以Taylor杆撞击实验结果为优化目标，通过高斯牛顿迭代优化，最终优化确定了炮钢材料动态本构模型参数。以最终动态本构模型参数为依据，通过Taylor杆冲击数值仿真与Taylor杆验证实验变形结果对比，验证了炮钢材料最终动态本构模型，模型预测试样变形与实验结果相对误差小于5%.

1 实验原理及方法

1.1 实验原理

SHPB实验中，通常采用的是很短的试样，应力波在试样中来回传播一次所用的时间与入射脉冲的长度相比要小得多，因此在入射脉冲作用过程中，试样内将有足够的时间发生多次的内反射，试样中的应力和应变能够很快地趋向均匀，所以在SHPB实验中，试样内部的应力波传播效应可以忽略，而利用入射、反射和透射脉冲来推导出试样中的应力、应变和应变率。SHPB实验装置示意图见图1.此装置由3根性能完全相同的弹性杆组成，它们分别是撞击杆、入射杆和透射杆。通过采用在入射杆和透射杆上贴应变片的方法，经过对应变片信号的放大和高速采集与存储，经过后处理可以得到所需的应力-应变曲线。

图1 SHPB实验装置示意图Fig.1 Schematic diagram of Hopkinson pressure bar

通常，应力波在试样中来回反射几次（3次以上），通过试样的力就可达到平衡。由于试样中波的传递时间相对加载波脉宽很小，故试样的变形可认为是均匀的。试样的动态应力-应变曲线完全可以通过弹性Hopkinson压杆上的应变脉冲，即入射应变εt（t）和反射应变εr（t）确定，如（3）式～（5）式所示［6］:

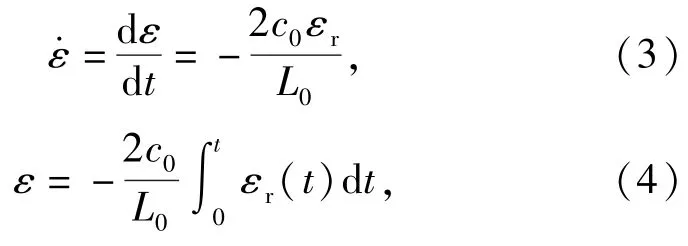
式中:L0为试样长度；c0为一维弹性波速，且，ρ0为撞击杆质量密度，E是弹性模量；A和 A0分别是试样和杆的横截面积。

1.2 实验准备

由于在SHPB测试中，惯性效应及试样与杆端的摩擦等会导致实验结果的不准确，因而在实验前必须合理设计、选择试样。通常情况下，由于圆柱形试样容易加工，因而人们更多地采用圆柱形试样进行实验，而确定试样的几何尺寸则需要综合考虑多方面因素。例如:通常对多晶体金属及其合金材料，试样尺寸必须是其一个典型的微观结构单元尺寸的10倍以上，而对于脆性材料试样，必须足够大以保障在达到应力平衡前试样不会提前破坏。因而，对于一套给定的SHPB实验系统，压杆直径最好是试样直径的2.4倍以上。这样虽然试样在压缩变形过程中长度缩短，而直径变大，但仍可以保证试样直径超过压杆直径前达到30%的真实应变。此外，试样的长径比也应当在0.5～1.0之间，太长的试样在实验过程中容易失稳。

SHPB实验系统使用的撞击杆、入射杆、透射杆直径相同，直径均为13 mm，其材料为高强度合金钢（18NiC350钢）。实验所用试样尺寸:动态压缩试样直径5 mm，长度4 mm；动态拉伸试样直径5 mm，长度31 mm.由于动态实验的分散性，研究中每一工况实验试样不少于15件。高温实验使用热电偶加热，低温实验使用液氮产生低温环境。考虑到本文篇幅，这里没有给出高低温实验的具体实施方法。图2为动态高温实验现场，图3为动态低温实验现场。

图2 动态高温实验现场Fig.2 Dynamic high temperature experimental site

图3 动态低温实验现场Fig.3 Dynamic low temperature experimental site

除了对试样的几何尺寸方面的要求外，试样的加工必须保证试样两个端面的平行度在0.01 mm以上，同时这两个端面应该有足够的光洁度以减小实验过程中端部摩擦的影响。还需要注意的是，由于在加工过程中，材料中难免会有残余应力存在，这有时也会给实验结果的准确性产生影响，因而在实验前对试样进行适当的热处理以减小残余应力的影响有时也是必要的。

试样准备好后，可以根据实验要求选择撞击杆合适的长度和速度。如果实验要得到的应变率为，那么可以根据（6）式估计撞击杆的撞击速度［7］:

式中:v是撞击杆的速度。如果实验要求的最大名义应变为ε，那么所需要的撞击杆长度为

式中:cb是撞击杆的弹性波速。

虽然利用（6）式、（7）式能够初步确定撞击杆的长度及撞击速度，但是对那些具有很高的屈服强度或者应变硬化明显的材料，需要适当地加长撞击杆，并且提高撞击速度。

2 实验结果及动态本构模型参数初步确定

2.1 实验结果

图4、图5、图6为压缩实验时3种应变率对应不同温度的应力-应变曲线。图7为同一应变率下的拉伸与压缩应力-应变对比曲线，图8为同一温度下，应变率从低到高流动应力的变化曲线。

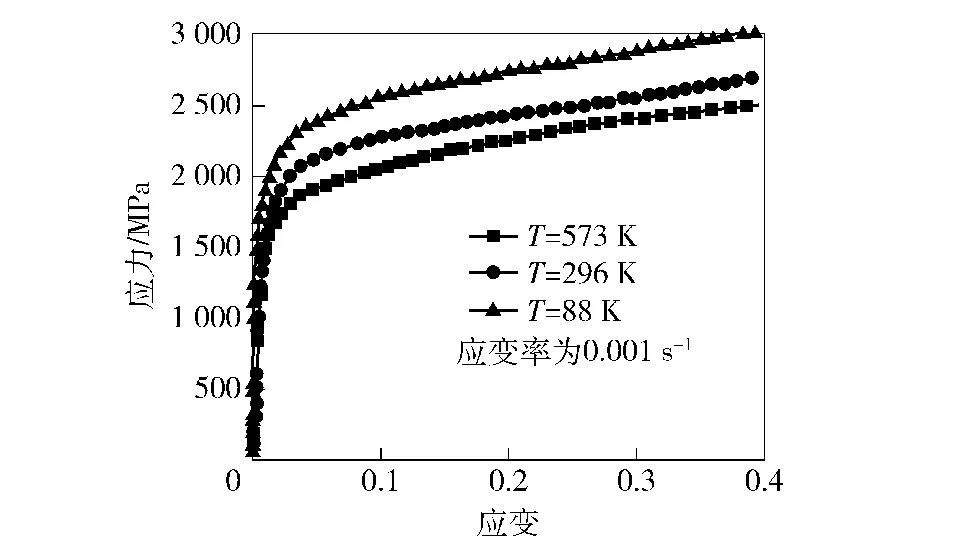
图4 同一应变率在不同温度下的压缩应力-应变曲线Fig.4 The compressive stress-strain curves at different temperatures and the same strain rate

当应变率为0.001 s-1时，PCrNi3MoA材料（炮钢材料）压缩屈服应力高于2 000 MPa，之后随着变形的增大，流动应力继续增大。随着实验温度的提高，屈服应力出现明显下降；而随着实验温度的降低，屈服应力出现明显上升（见图4）。在拉伸实验中，屈服应力为1 800 MPa左右，之后当流动应力超过1 900 MPa时开始颈缩，进而拉断。由此可以得出，在相同应变率和温度下，炮钢材料拉伸屈服应力一般要低于压缩屈服应力。

在应变率2 000 s-1下，炮钢材料的压缩屈服应力随着实验温度的变化并不明显（见图6），这主要是因为在高应变率动态实验中，加载速度较高，试样塑形变形在内部产生的热量来不及散失而使其处于绝热状态，从而使试样温度升高，而温升引起的温度热软化效应对冲了瞬态加载过程中部分应变硬化效应，从而降低了实验温度对压缩屈服应力的影响效应。

从图8炮钢材料在同一温度下不同应变率的压缩应力-应变实验曲线看出，炮钢材料的流动应力几乎不随应变率变化，应变率从0.001 1～2 000 s-1其流动应力-应变曲线几乎重合，进而说明炮钢材料的流动应力对应变率不敏感，从而可以推断在炮钢材料的J-C本构模型（1）式中，第2项对其流动应力影响很小。

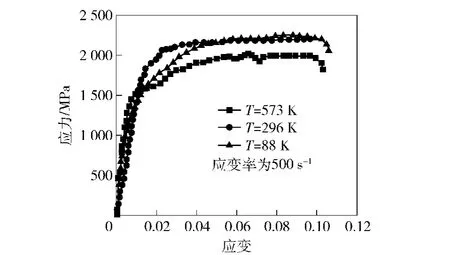
图5 同一应变率在不同温度下的压缩应力-应变曲线Fig.5 The compressive stress-strain curves at different temperatures and the same strain rate

图6 同一应变率在不同温度下的压缩应力-应变曲线Fig.6 The compressive stress-strain curves at different temperatures and the same strain rate

图7 同一应变率下的拉伸与压缩的应力-应变曲线Fig.7 The tensile-compressive stress-strain curves at the same strain rate

图8 同一温度在不同应变率下的压缩应力-应变曲线Fig.8 The compressive stress-strain curves at different strain rates and the same temperature

2.2 炮钢材料动态本构模型参数初步确定

J-C模型应用的一个显著优势即为参数相对较少，并且应变、应变率、温度三部分影响因素是解耦的，因此其参数的确定相对比较简单，J-C模型的具体形式见（1）式。式中A、B、C、n、m是5个待定参数，其中A、B和n表征了材料及其应变硬化特性，C表征了应变率敏感性，m表征了温度敏感性。这5个参数都是材料常数。J-C模型中的具体参数确定主要分3步完成:

第1步:取T=Tr，实验条件下的实验数据，（1）式简化为，其中A值一般可以通过σ0.2的值来确定，通过绘制ln（σ-A）与lnε曲线，并进行线性拟合，其中斜率即为参数n，而纵截距即为lnB的值，故可以得到A、B、n值。

第2步:在T=Tr时温度热软化项为0，即（1）式可以简化为

对（8）式进行分析，利用某一固定应变下流动应力与应变率的关系，通过绘制与曲线，并进行一次拟合，其中拟合直线斜率即为C值。

根据实验结果及上述步骤，初步确定了炮钢材料动态本构模型各个参数值，结果见表1.

表1 初步确定的炮钢材料动态本构模型参数Tab.1 The preliminarily obtained parameters of gun steel material dynamic constitutive model

3 动态本构模型参数优化及验证

3.1 动态本构模型验证实验

本构模型验证实验采用Taylor杆实验系统［1，8］，用平头圆柱形试样以一定速度正撞刚性靶平面，通过精确测量实验前后试样轴向不同部位的径向变形，与炮钢材料动态本构模型理论预测结果进行对比，验证模型预测结构动态响应的准确性。

验证实验中沿试样长度不同位置应变率会有不同，且连续变化，最大实验应变率达2 000 s-1，覆盖研究的应变率范围内。实验主要测试包括:1）测量变形后试件外形，其中包括轴向不同位置处的直径和试件剩余长度；2）测量试样撞靶时的速度。炮钢材料牌号为PCrNi3MoVA，试样直径10 mm、长度60 mm.Taylor杆实验系统及组成如图9所示，系统主要由发射器、试样、刚性靶、激光测速仪等组成，图10为验证实验系统。

图9 验证实验系统示意图Fig.9 Schematic diagram of verification experiment

根据要验证的动态本构模型应变率范围预估实验中试样的着靶速度，安装试样到弹托内固定防止试样与管壁接触，并使试样与推进气体分隔开，应用激光笔调试确保试样与靶板垂直撞击，安装并调试脱弹器使弹托与撞击试样在实验时能有效分离，脱弹器如图11所示。调节测试和发射系统到正常工作状态，按照预定的试样着靶速度调节发射机构气压完成实验。通过激光测速仪获得试样着靶速度，然后测量撞击后试样的变形用于与炮钢动态本构模型预测结果对比。图12为激光测速仪。

图10 验证实验系统Fig.10 Experimental system for verification

图11 脱弹器Fig.11 Test piece separator

图12 激光测速仪Fig.12 Laser velocimeter

3.2 动态本构模型参数优化

初步获得炮钢材料动态本构模型各个参数之后，再综合考虑应变率、应变、温度等方面的影响，以Taylor杆实验试样变形结果为优化目标，对初步确定的炮钢材料动态本构模型各参数B、C、n、m一起进行优化，其优化原则是初始确定的参数A不变，结果以满足设定的优化目标误差阈值6%为结束条件。优化程序框图见图13.

本构模型参数以（9）式所示的目标函数进行优化:

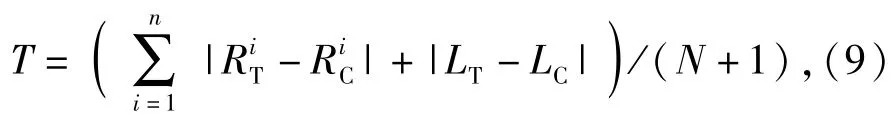
式中:RT、RC分别为实验后试件半径的实际测量值和对应点处有限元模拟计算值；LT、LC分别为实验后试件剩余长度的实际测量值和对应点处有限元模拟计算值；N为实验后试件直径实际测量数据总数。具体优化过程如下:

图13 本构模型参数优化程序框图Fig.13 The flow chart of parameter optimization program

1）设定目标阈值δ，利用优化前本构模型参量作初始本构参量。

2）将初始本构参量代入到LS-DYNA进行数值仿真，模拟出撞击后Taylor杆最终长度、半径以及未变形长度等外形数据。

3）将仿真外形数据与Taylor杆实验后试样外形数据代入目标函数（9）式，设定阈值δ.

4）若|Tc-Tn|≤δ，计算结束，初始本构参量通过验证。Tc与Tn分别表示当前的目标函数值与迭代下一步的目标函数值。

5）若|Tc-Tn|＞δ，利用G-N迭代法调整本构参量，将优化后本构参量设定为初始本构参量，再次执行第2、3步直到满足第4步。

最终获得优化后的炮钢材料动态本构模型参数，见表2.优化后的模型参数C值很小，进一步证明了前述的推断，即炮钢材料的流动应力对应变率不敏感。

3.3 验证实验结果

按照上述炮钢材料动态本构模型验证实验方法，获得了炮钢材料试样的变形结果。基于优化后炮钢材料动态本构模型参数（见表2），建立试样的数值仿真模型，靶体材料设置为刚性并施加位移约束，接触模式设置为单面的自动接触，分别施加与表3中4组实验相同的速度，按照文献［9］中第6章Taylor杆冲击数值仿真方法进行计算。整理数值计算与验证实验对比结果（见表3），炮钢材料动态本构模型预测与验证实验对比曲线如图14所示，二者的差异主要表现在撞击面端部最大半径以及撞击后剩余长度之间的差别。通过对比可看出，在实验撞击速度范围内，本文建立的炮钢材料动态本构模型预测与实验最大误差不超过5%，验证实验和数值仿真后试样的变形如图15所示。

表2 优化后炮钢材料动态本构模型参数Tab.2 The optimized parameters of gun steel material dynamic constitutive model

表3 炮钢动态本构模型预测与实验结果对比Tab.3 Comparison between the predicted and experimental results

图14 炮钢本构模型预测与实验对比曲线Fig.14 Comparison curve of predicted and experimental results

图15 试样变形对比Fig.15 The test and predicted sample deformations

4 结论

本文在宽温度（88～573 K）和大应变率范围（0.001～2 000 s-1）条件下，通过对炮钢材料的高温、高应变率耦合的静态和动态SHPB实验，初步获得炮钢材料动态本构模型基本参数。以Taylor杆实验结果为优化目标，通过进一步的模型参数优化，验证并最终确认了炮钢材料动态本构模型参数，最终模型预测试样变形与实验结果相对误差小于5%.验证结果表明，本文建立的炮钢材料动态本构模型能较真实地反映其动态响应，为火炮结构动态强度设计奠定了基础。

（

）

［1］ Meyers M A.材料的动力学行为［M］.张庆明，刘彦，黄风雷，等，译.北京:国防工业出版社，2006:225-230，259-260. Meyers M A.Dynamic behavior of materials［M］.ZHANG Qingming，LIU Yan，HUANG Feng-lei，et al，translated.Beijing: National Defense Industry Press，2006:225-230，259-260.（in Chinese）

［2］ 苏静，郭伟国，曾志银，等.超高强度钢AF1410塑性流动特性及其本构关系［J］.固体力学学报，2012，33（3）:265-272. SU Jing，GUO Wei-guo，ZENG Zhi-yin，et al.Plastic flow characteristics and constitutive relation for ultra high strength steel AF1410［J］.Chinese Journal of Solid Mechanics，2012，33（3）: 265-272.（in Chinese）

［3］ 张伟，魏刚，肖新科.2A12铝合金本构关系和失效模型［J］.兵工学报，2013，34（3）:276-282. ZHANG Wei，WEI Gang，XIAO Xin-ke.Constitutive relation and fracture criterion of 2A12 aluminum alloy［J］.Acta Armamentarii，2013，34（3）:276-282.（in Chinese）

［4］ 闫洪霞，高重阳.BCC金属物理型动态本构关系及在钽中的应用［J］.兵工学报，2010，31（增刊1）:149-153. YAN Hong-xia，GAO Chong-yang.A physically based constitutive model for BCC metals and its application in tantalum［J］.Acta Armamentarii，2010，31（S1）:149-153.（in Chinese）

［5］ 李国和，王敏杰，康仁科.Fe-36Ni高温高应变率动态力学性能及其本构关系［J］.材料科学与工艺，2010，18（6）:824-828. LI Guo-he，WANG Min-jie，KANG Ren-ke.Dynamic mechanical properties and constitutive model of Fe-36Ni invar alloy at high temperature and high strain rate［J］.Materials Science&Technology，2010，18（6）:824-828.（in Chinese）

［6］ Bobbili R，Madhu V，Gogia A K.Neural network modeling to evaluate the dynamic flow stress of high strength armor steels under high strain rate compression［J］.Defence Technology，2014，10（4）:334-342.

［7］ 郭伟国，李玉龙，索涛.应力波基础简明教程［M］.西安:西北工业大学出版社，2007:129-132. GUO Wei-guo，LI Yu-long，SUO Tao.Foundation concise course of stess wave［M］.Xi'an:Northwestern Polytechnical University Press，2007:129-132.（in Chinese）

［8］ 马晓青，韩峰.高速碰撞动力学［M］.北京:国防工业出版社，1998:135-144. MA Xiao-qing，HAN Feng.Dynamic of highspeed impact［M］. Beijing:National Defense Industry Press，1998:135-144.（in Chinese）

［9］ 时党勇，李裕春，张胜民.基于ANSYS/LS-DYNA8.1进行显式动力分析［M］.北京:清华大学出版社，2005:331-340. SHI Dang-yong，LI Yu-chun，ZHANG Sheng-min.The explicit dynamic base on ANSYS/LS-DYNA8.1［M］.Beijing:Tsinghua University Press，2005:331-340（in Chinese）

Dynamic Constitutive Model of Gun Steel Material and Its Verification

ZENG Zhi-yin，GAO Xiao-ke，LIU Peng-ke，YU Hua-sa
（Northwest Institute of Mechanical and Electrical Engineering，Xianyang 712099，Shaanxi，China）

The static and dynamic SHPB（split Hopkinson pressure bar）tests are made on a gun steel material at the temperature of 88～573 K and the strain rate of 0.001～2 000 s-1.The preliminarily obtained parameters of constitutive model of some gun steel material are verified and confirmed by the optimization procedure and Taylor impact test.The difference between the predicted and experimental results is less than 5%.The experimental results show that the proposed dynamic constitutive model can reflect the dynamic response of gun steel material under loads effectively.

ordnance science and technology；gun steel material；constitutive model；Hopkinson pressure bar test；Taylor impact test

O347.3

A

1000-1093（2015）11-2038-07

10.3969/j.issn.1000-1093.2015.11.004

2014-07-24

国家“973”计划项目（6133116）

曾志银（1957—），男，研究员。E-mail:zzy202@126.com