基于干扰观测器的电液位置伺服系统跟踪控制

刘龙，姚建勇，胡健，马大为，邓文翔

（南京理工大学机械工程学院，江苏南京210094）

基于干扰观测器的电液位置伺服系统跟踪控制

刘龙，姚建勇，胡健，马大为，邓文翔

（南京理工大学机械工程学院，江苏南京210094）

针对电液位置伺服系统存在匹配和不匹配模型不确定性的问题，提出一种基于滑模的模型不确定性补偿控制策略。通过设计滑模观测器估计电液位置伺服系统的匹配和不匹配模型不确定性，以在控制器设计中将其补偿，有效地削减控制器不连续项增益。将观测器滑模面引入到控制器滑模面中构造新的控制器滑模面，消除不确定性的估计误差，以保证控制器良好的动态性能。此外，不使用系统加速度信息，以降低可测噪声对跟踪性能的恶化。通过Lyapunov稳定性理论验证了闭环系统的全局稳定性。仿真结果显示，与积分滑模控制策略相比，所提方法能够补偿电液位置伺服系统中存在的匹配和不匹配模型不确定性，同时削弱滑模控制的抖振，具有良好的跟踪性能和较强的鲁棒性。

控制科学与技术；电液位置伺服系统；模型不确定性；滑模观测器；滑模控制

0 引言

电液伺服系统具有抗负载刚性大、响应快及功重比大等突出优点，在众多重要领域［1-2］内得到广泛运用。电液伺服系统是一个典型的非线性系统［3］，包含许多非线性特性［4］和建模不确定性［5］，其中建模不确定性包括参数不确定性和不确定性非线性等。近年来，随着电液伺服系统向高精度、高频响的方向发展，控制系统中存在的模型不确定性和非线性特性成为限制系统性能提升的重要因素。

为提高电液伺服系统跟踪性能，许多方法相继被提出。针对系统存在非线性特性，反馈线性化控制策略［6-7］通过在控制器设计中对非线性项进行精确补偿以使误差动态线性化。但实际系统的精确模型是不可能完全获知的，并且控制器中要使用系统加速度信息，增加了可测噪声对系统控制性能的影响。近年来，针对电液伺服系统中存在的模型不确定性，采用不敏感的滑模控制方法［8-9］开展的研究主要集中在系统中存在的匹配模型不确定性的补偿与控制［10-12］，而对于电液伺服系统中广泛存在的不匹配模型不确定性则考虑较少。对非线性系统中存在不匹配模型不确定性，Rubagotti等［13］提出积分滑模控制，设计积分形式的滑模面，通过增大控制器的鲁棒性来克服不匹配和匹配不确定性迫使系统状态到达滑模面。但通过增大不连续项增益的方法来增加滑模控制器的鲁棒性加剧了滑模控制的抖振问题，在实际运用中很可能激发系统存在的高频动态，使系统发散失稳。

基于以上分析，本文针对电液位置伺服系统存在匹配和不匹配模型不确定性的问题，提出一种基于滑模的模型不确定性补偿控制策略。通过设计滑模观测器估计电液位置伺服系统的匹配和不匹配模型不确定性，并在设计控制器过程中将其补偿，以削减控制器不连续项增益。同时不使用系统加速度信息，降低可测噪声对跟踪性能的恶化。增强了滑模控制方法运用在液压位置伺服系统中抵抗匹配和不匹配模型不确定性和非线性的能力，并通过仿真实验验证了控制器的有效性。

1 电液位置伺服系统数学模型

图1为基于干扰观测器的电液位置伺服系统结构。该系统通过伺服阀控制液压马达驱动惯性负载。

图1 基于干扰观测器的电液位置伺服系统结构Fig.1 The architecture of electro-hydraulic positioning servo system based on disturbance observer

根据牛顿第二定律，惯性负载的运动方程为

式中:m为惯性负载参数；pL=p1-p2为液压马达负载压力，p1和p2是液压马达两腔压力；A为液压马达的排量；B为粘性摩擦系数；是其他未建模干扰及未考虑的系统物理参数的偏差；y为惯性负载的位移；t为时间变量。

忽略液压马达的外泄漏，则液压马达两腔的压力动态方程为

式中:V1、V2分别为液压马达两腔的控制容积，V1= V01+Ay，V2=V02-Ay，V01和V02分别为液压马达两腔的初始容积；βe为有效油液弹性模量；Ct为内泄漏系数；q1（t）和q2（t）分别为p1和p2动态方程的建模误差；Q1和Q2分别为液压马达的进油腔流量和回油腔流量。

Q1和Q2与伺服阀位移xv的关系为

由于该系统采用的是高频响的伺服阀，阀芯位移与控制输入近似为比例环节即xv=kiu，ki为位移常数，u为控制输入电压，故（3）式可以写成:

式中:kt=kqki代表总的流量增益。

式中:系统物理参数m、B、βe、kt、V01、V02、Ct等系统参数在观测器和控制器的设计中使用的是名义值，其与真实值之间的偏差集中放在未建模项中，分别为d（x，t）和q（x，t）.其中:d（x，t）是系统的不匹配模型不确定性，包括外负载干扰、未建模摩擦、未建模动态等；q（x，t）是压力动态的建模误差，也即系统的匹配模型不确定性。各函数和参数定义如下:

为简化系统状态方程，定义:

则（5）式可写成:

系统控制器的设计目标是:给定系统参考信号yd（t）=xd（t），设计一个有界的控制输入u使系统在存在匹配和不匹配模型不确定性及非线性特性的情况下，系统的输出y=x1尽可能地跟踪参考信号xd（t）.为便于控制器设计，假设和引理如下:

假设1 系统参考指令信号xd（t）∈C3且有界。电液位置伺服系统在一般工况下工作，即液压马达两腔压力满足0＜pr＜p1＜ps，0＜pr＜p2＜ps；满足|pL|比ps足够小，以保证g（x）≠0.

假设2 不匹配模型不确定性d1（x，t）和匹配模型不确定性d2（x，t）均有界，即

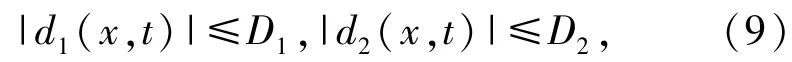
式中:D1、D2均为大小已知的正数。并且d1（x，t）的1阶导数存在。

引理1［14］如存在一连续正定函数V0（t）满足以下不等式:

则V0（t）在有限时间ts内收敛到平衡点，其中，

式中:α＞0；λ＞0；0＜γ＜1.

2 模型不确定性干扰观测器设计

2.1 不匹配模型不确定性干扰观测器设计

定义变量［14］s1:

式中:

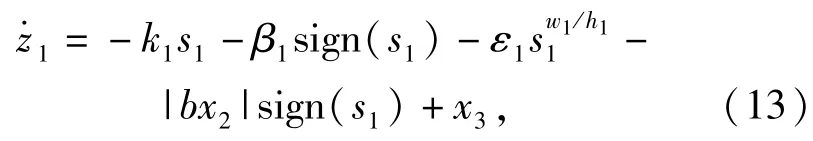
式中:w1、h1为正奇数且w1＜h1；k1、β1、ε1均为正数，β1＞D1.

由（8）式、（12）式、（13）式可得

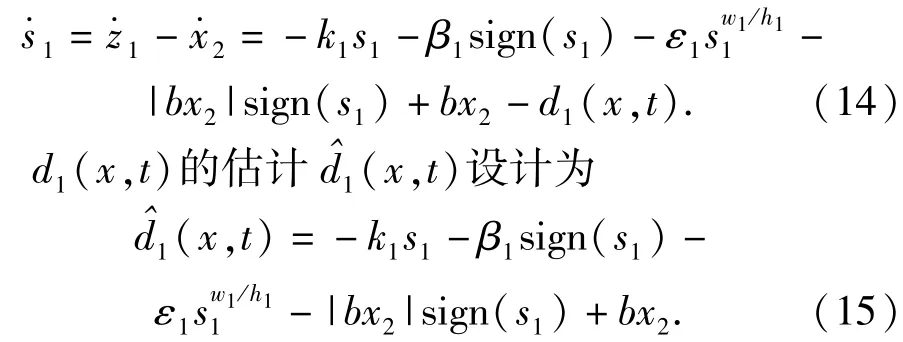
定理1 针对电液位置伺服系统不匹配模型不确定性设计终端滑模观测器（12）式、（13）式、（15）式，其观测误差将在有限时间内收敛。

证明 定义Lyapunov方程V1（t）:

又因β1＞D1，则有

由（8）式、（14）式、（15）式可得

根据引理1和（17）式，V1（t）将在有限时间内收敛到平衡点，即s1将在有限时间内收敛到平衡点。由于s1的有限时间收敛特性，结合（18）式，不匹配模型不确定性观测误差也是有限时间收敛的。

2.2 匹配模型不确定性干扰观测器设计

定义变量s2为

式中:

式中:w2、h2为正奇数且w2＜h2；k2、β2、ε2均为正数，β2＞D2.

由（8）式、（19）式、（20）式可得

定理2 针对电液位置伺服系统匹配模型不确定性设计终端滑模观测器（19）式、（20）式、（21）式，其观测误差将在有限时间内收敛。

证明 定义Lyapunov方程

又因β2＞D2，则有

由（8）式、（21）式、（22）式可得

根据引理1和（24）式、（25）式，类似于定理1的证明，匹配模型不确定性观测误差也是有限时间收敛的。

3 滑模控制器设计

定义电液位置伺服系统位置跟踪误差e0（t）、速度跟踪误差e1（t）、加速度跟踪误差e2（t）、加速度导数跟踪误差e3（t）分别为

定义控制器滑模面［4］s:

式中:c1、c2、c3均大于0，并且使得多项式χ3+c1χ2+ c2χ+c3是Hurwitz的，其中χ为复域内的微分算子。则有

设计控制器u为

式中:k为控制器不连续项增益，k＞0.由控制器表达式（32）式可知，控制器中并未使用到系统加速度信息，故在实际运用中将大幅减少测量噪声对系统跟踪性能的影响。

将（32）式代入（31）式可得

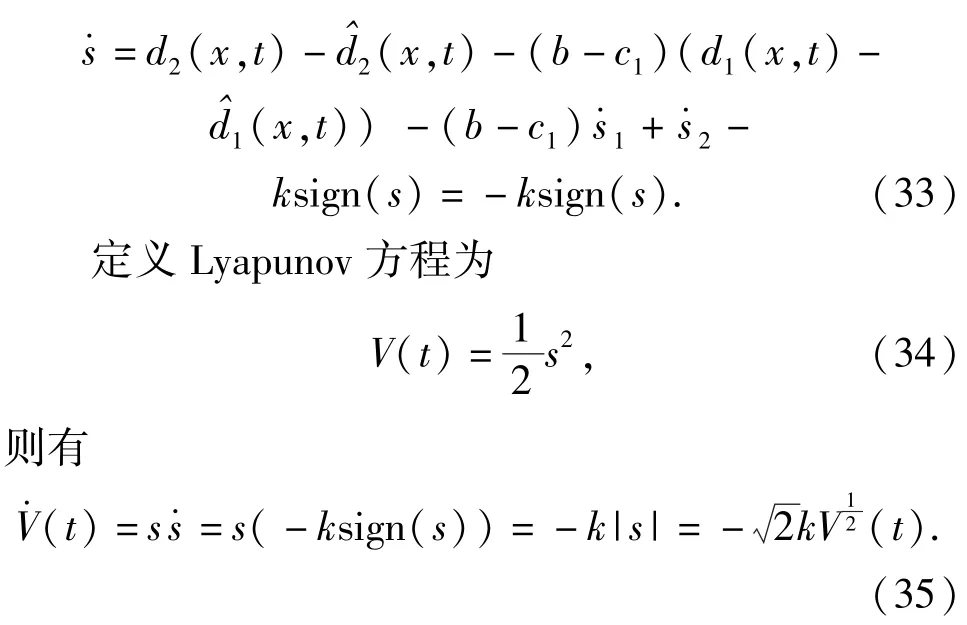
则s将在有限时间内收敛至0.由此可知，滑模控制器不连续项增益k仅须大于0即可满足滑模面到达条件［9］。而传统的滑模控制器不连续项增益必须满足大于不确定性上确界才能满足滑模面到达条件。

当s=0时有

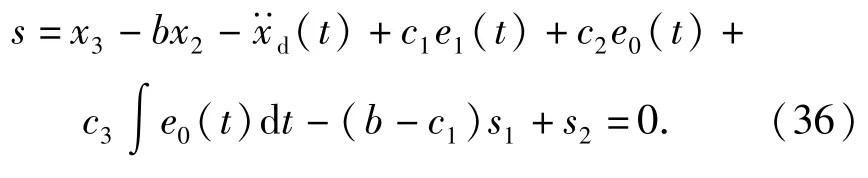
又因s1、s2也是有限时间内收敛的，设t1为s收敛至0的时刻，t2为s1收敛的时刻，t3为s2收敛的时刻，则存在t4=max｛t1，t2，t3｝，当经过t4时刻后有

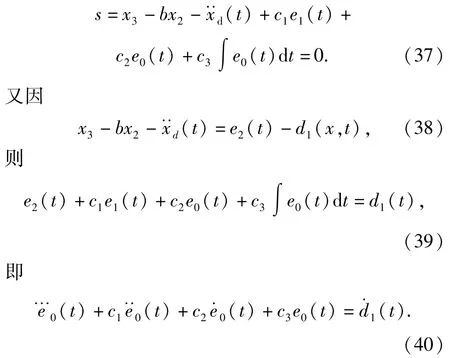
定理3 针对电液位置伺服系统（8）式，当假设1和假设2满足时，设计不匹配模型不确定性干扰观测器（12）式、（13）式、（15）式及匹配模型不确定性干扰观测器（19）式、（20）式、（22）式和滑模控制器（32）式，将有以下结论:

此时电液位置伺服系统位置跟踪误差e0（t）= x1-xd（t）在时间趋于无穷时趋于0.

此时e0（t）=x1-xd（t）在时间趋于无穷时收敛于一个一致稳定的界内。

4 仿真实验

为验证所提的控制策略，在Matlab/Simulink中搭建系统仿真模型。系统物理参数如表1所示，仿真步长设置为0.000 2 s.

表1 仿真系统参数Tab.1 Parameters of simulation system

给定系统的期望位置指令为:xd（t）=arctan（sin（t））·［1-exp（-0.01t3）］rad.

选取以下3种控制策略进行仿真对比:

1）本文所设计基于匹配和不匹配模型不确定性补偿的滑模控制器（UC-SMC），具体形式为（15）式、（22）式、（32）式；

2）文献［7］中反馈线性化控制器（FLC），具体形式如下:

控制量u表达式为

3）文献［13］中积分滑模控制器（I-SMC），具体形式如下:

滑模面σ1为

控制量u表达式为

针对结论1、结论2，分为以下两种工况进行仿真实验。

4.1 工况1

在该工况下，随着t→∞，不匹配模型不确定性为缓变量或常值，即不存在参数摄动，即各系统参数已知，取值见表1.

各控制策略参数取值:

1）UC-SMC参数:不匹配模型不确定性干扰观测器参数:k1=10 000，β1=5，ε1=0.05，w1=3，h1= 5；匹配模型不确定性干扰观测器参数:k2=10 000，β2=20，ε2=0.05，w2=5，h2=7；控制器参数:c1= 24，c2=192，c3=512，k=1.

2）FLC参数:l1=10，l2=10，l3=10.

3）I-SMC参数:c1=24，c2=192，c3=512，k= 150.

仿真结果如图2～图5所示。

图2 不匹配模型不确定性的观测和观测误差Fig.2 The observation and the observation error of unmatched modeling uncertainties

各控制器作用下系统位置的跟踪误差对比如图4所示，FLC的跟踪误差约为0.015 rad，I-SMC和UC-SMC的跟踪误差约为0.006 rad.显然，I-SMC和UC-SMC的控制精度高于FLC控制。这是因为FLC控制策略无模型不确定性补偿，系统存在的不确定性严重恶化FLC的跟踪性能。而UC-SMC和I-SMC二者的滑模面参数c1、c2、c3取值相同，故二者具有几乎相同的误差动态。结合图5，因I-SMC控制策略依靠提高不连续项增益的方法来克服模型不确定性，故其控制输入信号抖振较大，本文所提UC-SMC策略因使用滑模观测器补偿了模型不确定性，故可减小不连续项增益，削弱控制输入的抖振。

4.2 工况2

对于摩擦Ff，在工程中一般认为其与负载运动速度x2之间满足下式:

式中:对于非线性摩擦项Fc（x2），其摩擦动态非常复杂，相关文献［15］使用不连续摩擦模型来描述其效应，但在实际中，任何系统都不可能产生不连续的驱动力矩，故近年来，有学者开展了对摩擦的连续性建模和实验验证工作［16］，并取得了大量的成果和较好的实际运用效果［5，17］。基于此，本文在仿真模型中采用连续模型［18］来描述Fc（x2）的摩擦效应，同时将摩擦的其他效应归到建模误差项中处理，其中，Af为一常数，Sf（x2）为一连续函数。

图3 匹配模型不确定性的观测和观测误差Fig.3 The observation and the observation error of matched modeling uncertainties

图4 跟踪指令和跟踪误差Fig.4 Tracking command and tracking errors

图5 控制输入信号Fig.5 Control input

综上所述，在工况2中，系统存在参数摄动，仿真模型中取B=80 N·m·s/rad，βe=200 MPa，Ct= 9×10-12m3/（s·Pa），控制器中取B=60 N·m·s/rad，βe=700 MPa，Ct=10×10-12m3/（s·Pa）；仿真模型中添加摩擦项；未建模干扰取为；压力动态方程（2）式建模误差取为q1（t）=q2（t）= 6×10-6m3/s.同时，系统位置信号、压力信号存在幅值为2×10-6的随机噪声。

各控制策略参数取值如下:

1）UC-SMC参数:c1=24，c2=192，c3=512，k=1.

2）FLC参数:l1=10，l2=10，l3=10.

3）I-SMC参数:c1=24，c2=192，c3=512，k= 150.

仿真结果如图6和图7所示。图6为工况2时各控制策略作用下的位置跟踪误差，分析可知，采用FLC策略，系统的跟踪效果不佳，位置跟踪误差约为0.1 rad.UC-SMC和I-SMC的位置跟踪误差约为0.005 2 rad，二者具有几乎相同的误差动态，同时，由于，故所提UC-SMC的跟踪误差将收敛于接近零点的很小界内，保证良好的跟踪精度。图7为工况2下系统控制输入曲线，分析可知，与I-SMC相比，UC-SMC能大幅度削弱控制输入的不连续项增益。

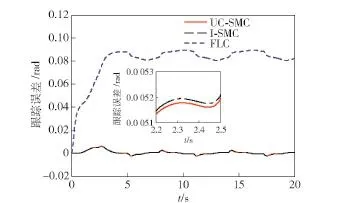
图6 工况2时跟踪误差Fig.6 Tracking error in Case 2

图7 工况2时控制输入信号Fig.7 Control input in Case 2

5 结论

针对电液位置伺服系统存在匹配和不匹配模型不确定性及非线性特性的问题，提出一种基于滑模的模型不确定性补偿控制策略。设计滑模观测器估计系统的匹配和不匹配模型不确定性，基于Lyapunov稳定性理论证明观测的准确性。通过构造新的滑模面来设计滑模控制器，在控制器中补偿系统存在的模型不确定性。不使用系统加速度信息的同时大幅度削减滑模控制器的不连续项增益。使得闭环系统在同时存在模型不确定性及非线性特性的情况下获得全局稳定和渐近跟踪性能，增强了滑模控制方法运用在电液位置伺服系统中抵抗匹配和不匹配模型不确定性和非线性的能力。仿真结果显示，与积分滑模控制策略相比，该方法能够补偿电液位置伺服系统中存在的匹配和不匹配模型不确定性，大幅度削弱滑模控制的抖振，同时具有较强的鲁棒性和良好的跟踪性能。

（

）

［1］ Yao J Y，Jiao Z X，Yao B，et al.Adaptive nonlinear optimal compensation control for electro-hydraulic load simulator［J］.Chinese Journal of Aeronautics，2010，23（6）:720-733.

［2］ Timo S，Ari S.A passive method to stabilize an airborne vehicle［J］. Defence Technology，2014，10（2）:124-130.

［3］ Merritt H E.Hydraulic control systems［M］.New York:Wiley，1967.

［4］ 管成，朱善安.一类非线性系统的微分与积分滑模自适应控制及其在电液伺服系统中的应用［J］.中国电机工程学报，2005，25（4）:103-108. GUAN Cheng，ZHU Shan-an.Derivative and integral sliding mode adaptive control for a class of nonlinear system and its application to an electro-hydraulic servo system［J］.Proceedings of the CSEE，2005，25（4）:103-108.（in Chinese）

［5］ Yao J Y，Jiao Z X，Ma D W.High accuracy tracking control of hydraulic rotary actuators with modelling uncertainties［J］.IEEE/ ASME Transactions on Mechatronics，2014，19（2）:633-641.

［6］ 吴跃飞，马大为，乐贵高.控制受限的火箭炮位置伺服系统鲁棒自适应反步控制［J］.兵工学报，2013，34（4）:477-483. WU Yue-fei，MA Da-wei，LE Gui-gao.Robust adaptive backstep-ping control for rocket launcher position servo system with constraint control［J］.Acta Armamentarii，2013，34（4）:477-483.（in Chinese）

［7］ 杨俊华，吴捷，胡跃明.反步方法原理及在非线性鲁棒控制中的应用［J］.控制与决策，2002，17（增刊）:641-648. YANG Jun-hua，WU Jie，HU Yue-ming.Backstepping method and its applications to nonlinear robust control［J］.Control and Decision，2002，17（S）:641-648.（in Chinese）

［8］ 高为炳.变结构控制理论基础［M］.北京:中国科学技术出版社，1990:74-83. GAO Wei-bing.Variable structure control theoretical basis［M］. Beijing:China Science and Technology Press，1990:74-83.（in Chinese）

［9］ 刘金琨，孙富春.滑模变结构控制理论及其算法研究与进展［J］.控制理论与应用，2007，24（3）:407-418. LIU Jin-kun，SUN Fu-chun.Research and development on theory and algorithms of sliding mode control［J］.Control Theory&Applications，2007，24（3）:407-418.（in Chinese）

［10］ Kim H M，Choi J.Robust tracking control for hydraulic actuator using backstepping sliding mode control［J］.Journal of Advanced Mechanical Design，Systems，and Manufacturing，2014，8（2）: 1-8.

［11］ Wang X，Sun X，Li S，et al.Finite-time position tracking control of rigid hydraulic manipulators based on high-order terminal sliding mode［J］.Proceedings of Institution of Mechanical Engineers，Part I-Journal of Systems and Control Engineering，2012， 226（3）:394-414.

［12］ Komsta J，Van Oijen N，Antoszkiewicz P.Integral sliding mode compensator for load pressure control of die-cushion cylinder drive［J］.Control Engineering Practice，2013，21（5）:708-718.

［13］ Rubagotti M，Estrada A，Castaños F，et al.Integral sliding mode control for nonlinear systems with matched and unmatched perturbations［J］.IEEE Transactions on Automatic Control，2011，56（11）:2699-2704.

［14］ Chen M，Wu Q X，Cui R X.Terminal sliding mode tracking control for a class of SISO uncertain nonlinear systems［J］.ISA Transactions，2013，52（2）:198-206.

［15］ De Wit C C，Olsson H，Astrom K J，et al.A new model for control of systems with friction［J］.IEEE Transactions on Automatic Control，1995，40（3）:419-425.

［16］ Makkar C，Dixon W E，Sawyer W G，et al.A new continuously differentiable friction model for control systems design［C］∥Proceedings of the 2005 IEEE/ASME International Conference on Advanced Intelligent Mechatronics.CA，US:IEEE，2005: 600-605.

［17］ Yao J Y，Deng W X，Jiao Z X.Adaptive control of hydraulic actuators with LuGre model based friction compensation［J］.IEEE Transactions on Industrial Electronics，2015，62（10）:6469-6477.

［18］ Yao B，Bu F，Reedy J，et al.Adaptive robust control of singlerod hydraulic actuators:theory and experiments［J］.IEEE/ ASME Transactions on Mechatronics，2000，5（1）:79-91.

Tracking Control for Electro-hydraulic Positioning Servo System Based on Disturbance Observer

LIU Long，YAO Jian-yong，HU Jian，MA Da-wei，DENG Wen-xiang
（School of Mechanical Engineering，Nanjing University of Science and Technology，Nanjing 210094，Jiangsu，China）

A kind of modeling uncertainties compensation control strategy based on sliding mode is proposed for electro-hydraulic positioning servo system with matched and unmatched modeling uncertainties. A sliding mode observer is designed to estimate the matched and unmatched modeling uncertainties of electro-hydraulic positioning servo system and compensate the uncertainties during the design of the sliding mode controller，thus effectively weakening the discontinuous term gain.The sliding surface of observer is introduced to the sliding surface of controller to construct a new controller sliding surface and eliminate the estimation error of uncertainties so that the good dynamic performance of the controller can be ensured.Besides，the deterioration of tracking performance，which comes from the measured noise，can be reduced without system acceleration.Finally，the global stability of the closed-loop system is verified by the Lyapunov stability theory.Simulation results show that the matched and unmatched modeling uncertainties of the electro-hydraulic positioning servo system can be compensated by the proposed method compared with the integral sliding model control strategy.At the meantime，the chattering of sliding mode control is weakened，and the system possesses good tracking performance and strong robustness.

control science and technology；electro-hydraulic positioning servo system；modeling uncertainty；sliding mode observer；sliding mode control

TP273

A

1000-1093（2015）11-2053-09

10.3969/j.issn.1000-1093.2015.11.006

2015-03-29

国家自然科学基金项目（51305203）；江苏省自然科学基金项目（BK20141402）；中国博士后科学基金项目（2014M551593）

刘龙（1989—），男，硕士研究生。E-mail:liulong_njust@163.com；姚建勇（1984—），男，讲师。E-mail:jerryyao.buaa@gmail.com