火炮发射环境下弹载光电器件结构动态响应研究

宁全利，蒋滨安，梁希，李俊，3

（1.陆军军官学院高过载弹药制导控制与信息感知实验室，安徽合肥230031；

2.燕山大学建筑工程与力学学院，河北秦皇岛066004；3.陆军军官学院二系，安徽合肥230031）

火炮发射环境下弹载光电器件结构动态响应研究

宁全利1，蒋滨安1，梁希2，李俊1，3

（1.陆军军官学院高过载弹药制导控制与信息感知实验室，安徽合肥230031；

2.燕山大学建筑工程与力学学院，河北秦皇岛066004；3.陆军军官学院二系，安徽合肥230031）

为了研究弹载光电器件抗高过载机理，针对火炮发射环境特点，以某型特种弹所用弹载光电器件为例，建立了加装减载组件的弹载光电器件有限元分析模型并进行仿真分析。采用应力波理论，建立了反映弹载光电器件动力学过程的理论分析模型，计算求解作用于镜头的应力、相对位移和相对速度等，得到了弹载光电器件的动力学响应。结果表明：数值计算与仿真模拟结果有较好的一致性，验证了所建立的理论分析模型的正确性，可用于火炮发射环境下不同弹载器件的动态特性研究和抗高过载设计的理论分析。

兵器科学与技术；弹载光电器件；数值计算；应力波；火炮发射

0 引言

弹载光电器件是炮兵新型弹药中一类重要的组成单元，在火炮发射时，随同弹丸承受上万g的瞬时高过载，其安全与否直接关系到该类弹药使用的可靠性。对火炮发射环境下弹载光电器件动态响应进行研究，是弹载器件抗过载机理研究的一项重要内容，也是解决该类器件在高过载弹药中可靠应用的基础和前提［1］。

由于火炮发射环境下，弹丸在火炮膛内的运动时间通常在几毫秒到十几毫秒之间，而一般冲击过程的时间量级通常在数百微秒左右，因此不能简单移植冲击动力学有关理论来研究火炮发射环境下弹载光电器件的动态响应，需要根据火炮具体的发射条件和弹载光电器件的装配情况进行分析。由于实弹试验组织程序复杂，且弹丸内装各类器件的动态响应过程难以检测，目前也无其他有效的测试和验证手段。本文针对火炮发射环境下弹载光电器件的动态响应，以某型特种弹所用弹载光电器件为例，采用LS-DYNA有限元分析软件对该器件及其减载组件进行建模仿真，并与采用应力波理论得到的数值计算结果进行了对比，验证理论分析方法的正确性。

1 弹载光电器件的动态响应数值仿真

1.1 载荷环境的确定

不同口径的身管火炮，采用不同发射装药时，弹丸在膛内的加速度随时间变化曲线均存在着较大不同［2-4］。为研究问题的方便，以某型火炮2号装药为例，将弹丸发射时在膛内的加速度时程曲线拟合为折线，如图1所示，过载持续时间为10.5 ms、峰值为10 000 g，峰值对应的时刻为4.1 ms.

1.2 有限元模型的建立和分析

研究所用的弹载光电器件为某型特种弹所用的光学镜头，镜头旋拧在由铝合金制成的固定座上，减载组件采用多片内心中空的圆形橡胶垫叠合组成。镜头及其固定座、减载组件置于铝质套筒内，并采用环形扣板固定。为防止反向冲击，在镜头固定座和扣板之间加装一片橡胶垫。在有限元分析中，镜片采用光学玻璃材料模型，镜头其他的部分采用工程塑料模型，镜头固定座、铝制套筒和扣板采用弹性体材料模型，橡胶采用Mooney-Rivlin不可压缩模型，建立的加装减载组件的弹载光电器件有限元分析模型如图2、图3所示。

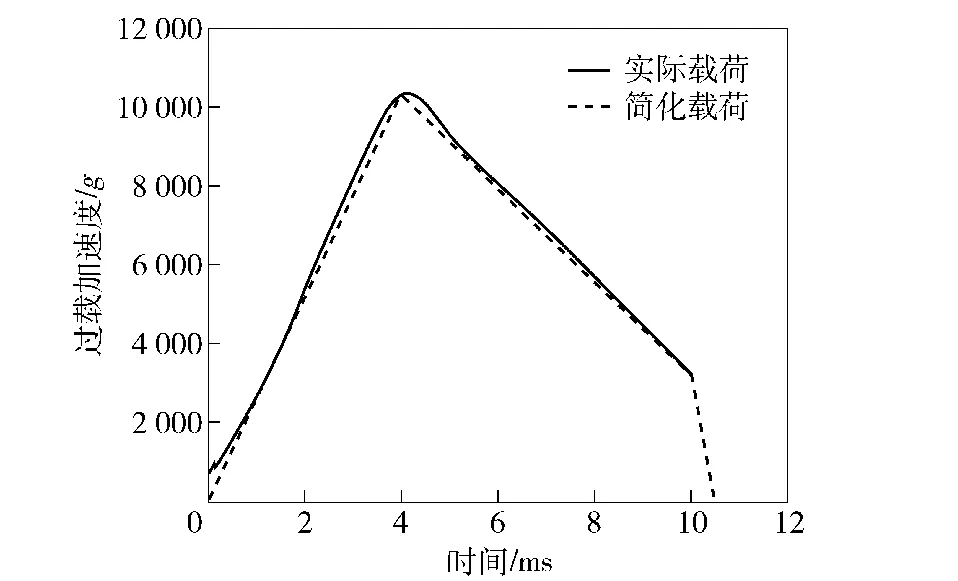
图1 火炮发射环境下弹丸在膛内的加速度时程曲线Fig.1 Acceleration vs.time

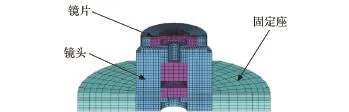
图2 弹载光电镜头及其固定座有限元模型Fig.2 Finite element model of projectile-borne device

经仿真计算，试件在过载持续时间10.5 ms、峰值10 000 g的冲击载荷作用下，结构变形如图4所示。从图4中可以看出，减载组件在第4.3 ms时刻压缩量达到最大，较载荷峰值有一定的延迟，压缩量最大值为4.57 mm.之后减载组件开始反弹，直至镜头底座上的橡胶垫撞到套筒扣板。橡胶垫反弹后，基本能够恢复原貌。

从仿真分析结果可知:在载荷作用时间为10.5 ms、峰值为10 000 g的火炮发射环境下，弹载光电器件和减载组件之间存在相互运动。这是因为在加载力开始作用的时候，试件中的减载组件先被压缩，弹载光电器件与套筒扣板分离，这时在弹载光电器件端面形成了自由面，应力即被卸载。在整个加载过程中，弹载光电器件上应力不断被加载和卸载，从而形成振荡运动，当加载力由大变小并开始衰减时，被压缩的减载组件逐渐复原，直至弹载光电器件与套筒扣板发生撞击，此时作用于镜片上的应力会突然增大。

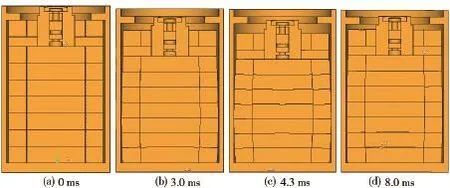
图4 减载组件变化时间图（10.5 ms，10 000 g）Fig.4 Load-relieving subassembly vs.time（10.5 ms，10 000 g）

2 理论模型的建立和数值计算

2.1 理论模型的建立

假设减载组件的截面受力不变形，弹载光电器件以易碎的镜头表征其破坏极限，当镜头所受应力达到破坏极限时即视为失效。建立如图5所示的弹载光电器件动态响应等效模型，A、B、C、D杆分别表示固体本件、减载组件、弹载光电器件和套筒，A和D固联，视为同步运动。设作用于A杆的外载为σ（t），B杆的长度为L、截面积为S、密度为ρ、应力波速为c，C杆为刚体，质量为m，C杆与D杆可接触可分离。

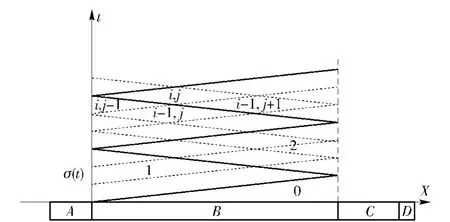
图5 应力波的特征线Fig.5 Characteristic lines of stress wave

2.2 理论模型的求解

由于外载σ（t）是持续变化的，在弹载光电器件内部也会出现持续变化的应力波传播，而传播过程应满足应力波的相容关系和结构本身的边界条件，这样只需知道初值条件，结合相容关系和边界条件，即可逐一求解任意时刻的应力状态，从而得到弹载光电器件的动力学响应。

2.2.1 初值条件和边界条件

如图5所示，在B杆内，其左右两端满足两个不同的边界条件，在AB截面时，应力值为输入应力σ（t），在BC截面时，应满足介质连续条件和受力平衡的边界条件［5］:

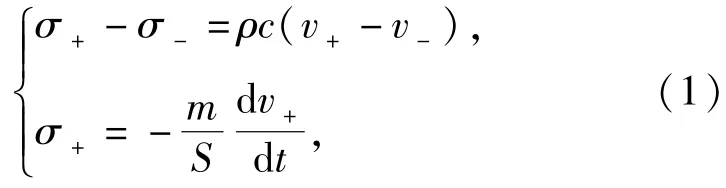
式中:v为质点速度，下标“+”表示应力波前状态，下标“-”表示应力波后状态。

随时间变化的σ（t）会使应力波在传播中持续变化，为了求解应力波的传播过程，按图5所示，将计算区域离散分化成若干个子区域，每一个子区域内部的应力状态皆相同，相邻子区域满足相容关系。为得到σ，将（1）式展开，区域0为初始状态，将每一个时间周期划分为k等分，以区域编号ij为例，i∈｛1，2，3，…｝，j∈｛1，2，3，…，k+1｝，子区域ij满足如下的相容关系:

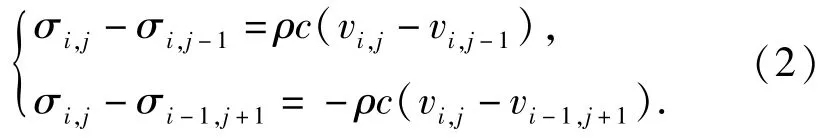
可得弹载光电器件满足的边界条件差分格式为

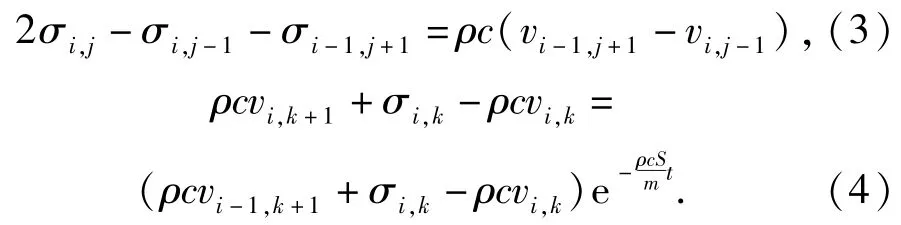
2.2.2 数值计算方法

理论上，选取的k值越大，代表划分的越细致，数值计算也就越精确，对于线弹性体，求解（3）式、（4）式，即可以求出整个计算区域的应力状态。而对于粘弹性材料，应变率效应不能忽略，具体来说，对于粘弹性材料的动力学响应，应满足连续方程、运动方程和材料的本构方程，构建其差分格式如下:

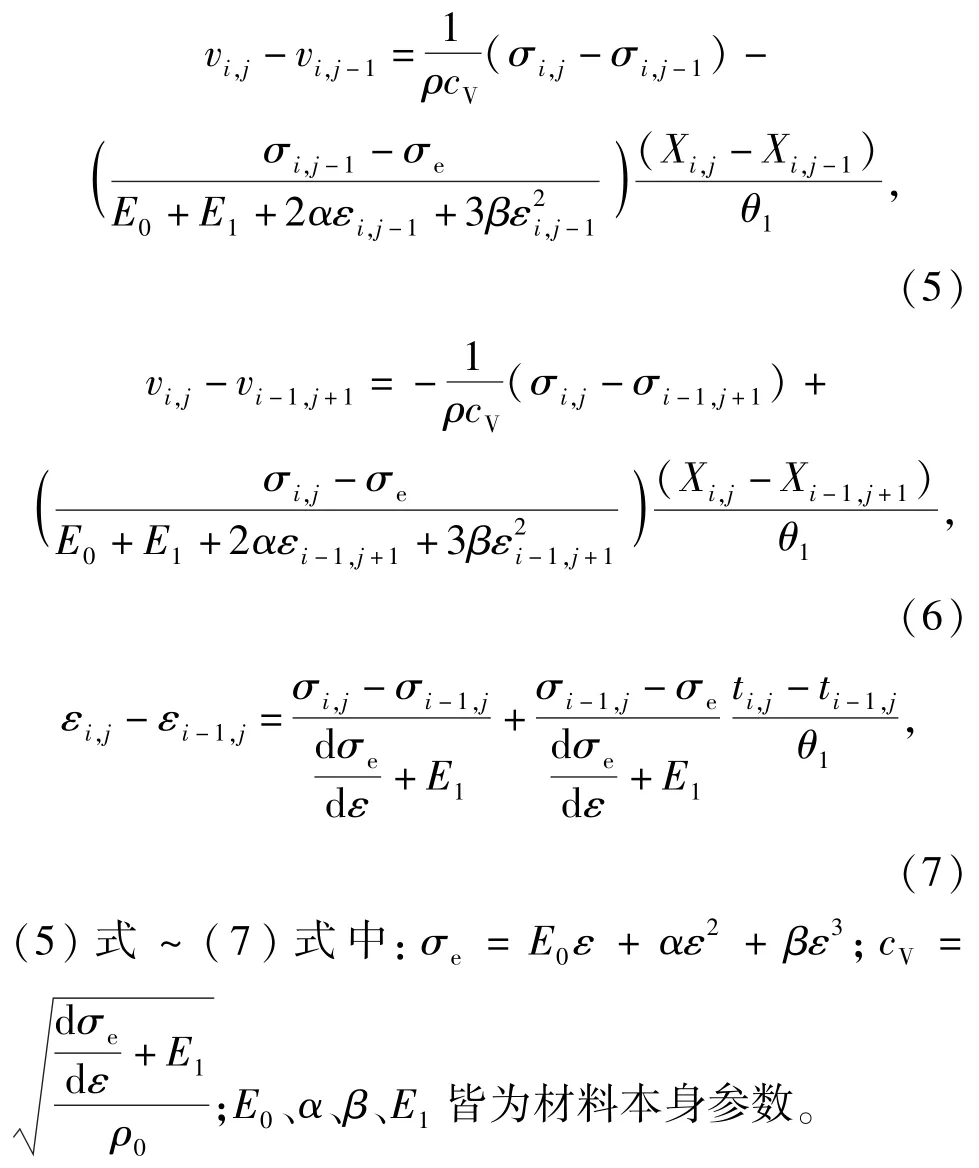
2.2.3 计算程序设计

基于上述离散求解方法可知:目标子区域的应力状态，都依赖于其周围子区域的应力状态，而任意子区域的应力状态，也只会影响其相邻的4个子区域，介于这样的力学性质，通过构建差分方程组（5）式～（7）式，并使用FORTRAN90编写基于Lagrange坐标下的数值计算程序来求解，即可得到作用于弹载光电器件的应力σ、应变ε和质点速度v，也就知道了火炮发射环境下弹载光电器件的动力学响应。

3 数值计算与仿真结果的对比

按照弹丸实际结构和载荷环境，将加载力、弹载光电器件及其减载器件尺寸参数等代入计算方程进行求解，采用数值计算与仿真模拟两种方法，分别得到作用于镜头上的最大应力和减载组件最大压缩量结果见表1.数值计算时，外载σ（t）将采用图1简化加载条件，将实际加载环境简化为3条线段的组合，4个端点坐标为（0 ms，0 g）、（4.3 ms，10 000 g）、（10 ms，3 700 g）以及（10.5 ms，0 g），以此4个端点组成的3条线段，即为外载σ（t）的函数值曲线。

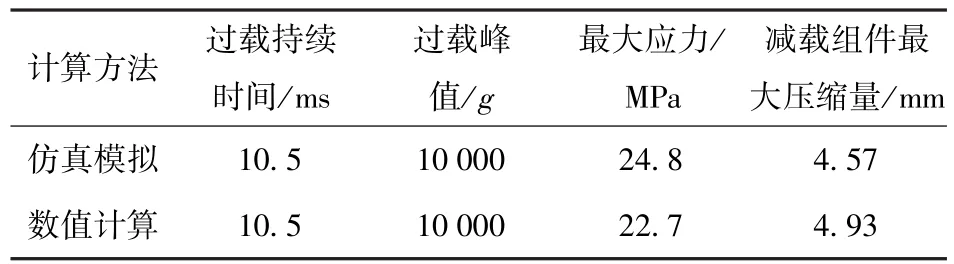
表1 计算结果对比Tab.1 Simulated and calculated results

图6是数值计算和仿真模拟得到的镜头相对位移、相对速度曲线对比，从图中可以看出，两种不同求解方法得到的计算结果一致性较好，但也存在一定误差，主要来源于参数的设置和算法的区别。此外，从图6（b）中可以发现，在加载力开始作用时，橡胶垫振荡压缩，镜头相对速度为负值，在4.3 ms时刻，即橡胶垫压缩量达到最大后，橡胶垫振荡复原，镜头相对速度由负值变为正值，振幅与加载力的变化率直接相关，而镜头在运动过程中不断振荡，是由于镜头受到持续不断的加载波和卸载波作用。当加载力结束后，镜头的相对速度出现剧烈变化，是由于镜头反弹使镜头底座上的橡胶垫与套筒扣板碰撞所致。

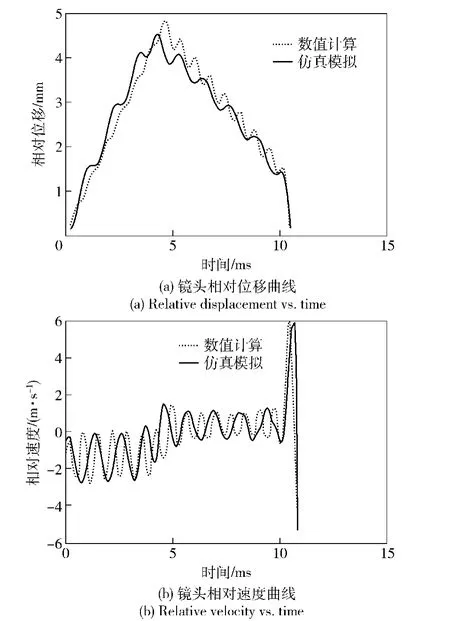
图6 数值计算和仿真模拟结果对比Fig.6 Calculated and simulated relative velocities and displacements of camera

4 结论

1）对火炮发射环境下弹载光电器件动态响应进行研究，是弹载器件抗过载机理研究的一项重要内容。本文以某型特种弹为例，采用应力波理论，建立了弹载光电器件的动力学分析模型，数值计算与仿真模拟结果具有较好的一致性，验证了理论分析方法的正确性，为火炮发射环境下弹载器件的动态特性研究提供了一种有效的理论分析和计算方法。

2）通过仿真模拟和数值计算可知，加装减载组件的弹载光电器件在弹丸发射过程中，在应力波作用下做持续振荡运动，振荡幅值会随着加载力的变化率增大而增大，而且在加载力结束后，镜头会出现较强反弹。此外，通过本文建立的理论分析模型，可在已知减载组件材料属性、几何尺寸和弹载器件质量等参数情况下，即可通过求解方程，得到弹载器件在火炮发射环境下的运动和受力情况，为不同类型弹载器件的抗高过载设计提供参考和借鉴。

（

）

［1］ 钱立志.信息化炮弹技术［M］.北京:解放军出版社，2006: 24-25. QIAN Li-zhi.Informatization artillery technology［M］.Beijing: Chinese People's Liberation Army Publishing House，2006:24-25.（in Chinese）

［2］ 金志明.枪炮内弹道学［M］.北京:北京理工大学出版社，2004:35-36. JIN Zhi-ming.Gun ballistics［M］.Beijing:Beijing Institute of Technology Press，2004:35-36.（in Chinese）

［3］ 宁全利.高过载环境下弹载光电器件结构动态响应研究［D］.合肥:陆军军官学院，2014:35-36. NING Quan-li.Research on structural dynamical response of projectile-based equipment under high overload［D］.Hefei:Army Officer Academy of PLA，2014:35-36.（in Chinese）

［4］ Jayasooriya R，Thambiratnam D P，Perera N J，et al.Blast and residual capacity analysis of reinforced concrete framed buildings［J］.Engineering Structures，2011，33（12）:3483-3495.

［5］ 王礼立，任辉启，虞吉林，等.非线性应力波传播理论的发展及应用［J］.固体力学学报，2013，34（3）:217-240. WANG Li-li，REN Hui-qi，YU Ji-lin，et al.Development and application of the theory of nonlinear stress wave propagation［J］. Chinese Journal of Solid Mechanics，2013，34（3）:217-240.（in Chinese）

The Structural Dynamic Response of Projectile-borne Optoelectronic Devices during Launching

NING Quan-li1，JIANG Bin-an1，LIANG Xi2，LI Jun1，3
（1.Laboratory of Guidance Control and Information Perception Technology of High Overload Projectiles，Army Officer Academy of PLA，Hefei 230031，Anhui，China；2.College of Civil Engineering&Mechanics，Yanshan University，Qinhuangdao 066004，Hebei，China；3.Department 2，Army Officer Academy of PLA，Hefei 230031，Anhui，China）

In order to study the anti-high-overload mechanism of projectile-borne optoelectronic devices，a numerical simulation model of projectile-borne opto-electronic devices is established according to the artillery launching environmental characteristics.A theoretical analysis model of projectile-borne optoelectronic devices is also established to solve the stress，strain and relative velocity of projectile-borne optoelectronic devices.The result shows that the numerically calculated results are in good agreement with the simulated results to verify the correctness of the theoretical analysis model.The proposed model can be used for the reseasch on the dynamic characteristics of the projectile-borne devicess and the theoretical analysis of anti-high-overload design.

ordnance science and technology；projectile-borne optoelectronic device；numerical simulation；stress wave；artillery launching

TJ410.3

A

1000-1093（2015）11-2185-05

10.3969/j.issn.1000-1093.2015.11.025

2015-01-18

国家自然科学基金项目（11172331）

宁全利（1978—），男，副教授。E-mail:522736949@qq.com