有限使用时间内预防性维修策略优化

盖京波，孔耀

（1.哈尔滨工程大学航天与建筑工程学院，黑龙江哈尔滨150001；2.中国电子科技集团公司第54研究所，河北石家庄050081）

有限使用时间内预防性维修策略优化

盖京波1，孔耀2

（1.哈尔滨工程大学航天与建筑工程学院，黑龙江哈尔滨150001；2.中国电子科技集团公司第54研究所，河北石家庄050081）

机械装备一般都是可维修设备。采取积极有效的预防性维修，合理安排预防性维修活动，对于减少装备的故障次数及提高使用率具有重要的现实意义。以在有限使用时间区间内工作的机械装备为研究对象，分别从维护成本及综合考虑维护成本和可靠性两个方面建立了预防性维修优化模型，并利用非线性优化软件对其进行了求解，确定机械装备在有限工作时间区间内最优的预防性维修次数以及预防性维修周期。算例表明，所提出的预测预防性维修次数和周期的方法是可行的，可为机械装备制定预防性维修大纲、预测机械装备使用寿命提供参考。

兵器科学与技术；有限时间；维修策略；优化

0 引言

预防性维修是在装置频繁出现故障之前，综合采取各种可能的技术、手段和管理办法，使装置的性能得以完善，最终实现充分延长使用时间和提高使用率的目的。

维修策略是各种可用方法、手段的总称。预防性维修策略研究已成为重要研究领域，自20世纪50年代就引起了国内外学者的重视。1960年，Barlow等首次提出最小维修的概念及定时维修的理念，并建立了最优维修周期的模型［1］。随后越来越多的学者提出了更多模型，运用马尔可夫过程、随机点过程、几何过程等数学基础理论来确定最优的预防性维修间隔周期T及近似无限使用情况下的维修次数N［2-3］.但是，基于产品无限使用这一假设得到周期T和次数N明显是不符合实际情况的。产品的自然寿命是有限的，并非无限使用。并且，初期大多数研究仅是从经济性这个角度考虑，建立模型来确定最优的周期T和次数N，而忽略了对于一些重要装置（例如国防设备）需要考虑可靠性的要求。

1 问题提出

早期的研究为了研究方便对优化模型常采取两种较为理想的假设:1）修复后装置修复如新；2）装置故障后采取的是基本维修，只是使装置的功能恢复了，而并没有改变装置的故障率。这两种假设都有一定的局限性，对于一些劣化系统，这两种假设明显是不适用的。针对劣化系统的故障率，文献［4-6］分别提出了役龄因子和故障率递增因子。Malik［4］认为经过第n次预防性维修之后，装置的故障率变为λn+1（t）=λn（t-αNTN），0＜t＜TN+1.

Nakagawa［5］则提出，经过第n次预防性维修后，装置的故障率变为λn+1（t）=bnλn（t），0＜t＜TN+1，式中:bn＞1为故障率递增因子。经过预防性维修后装置的故障率虽然变为0（修复如新）.但是，故障率函数的变化率增大了。这比较符合实际使用中越修越坏的状况。基于故障率递增因子的顺序预防性维修决策取决于装置的故障率状态［7］。因此，该维修方法操作性较强，大多数对于不完全维修研究采取的是此研究方法。

2 模型假设

假设1 装置投入使用时是全新的；

假设2 忽略装置故障维修时间，因为其相对时间T很小；

假设3 预防性维修使装置的故障率下降到偶然故障阶段的故障率（修复如新），但同时增大了故障率函数的变化率；

假设4 对于预防性维修周期内发生的故障只采取故障维修措施，不改变装置的故障率以及装置的故障率函数，且故障维修时间不计。

整个使用时间［0，T］内装置的运行维修流程如图1所示。

图1 有限使用时间［0，T］内装置工作维修时序图Fig.1 Timing sequence chart of work maintenance of device in finite time horizon of［0，T］

3 以成本为目标的优化模型

3.1 模型构建

机械装置在使用过程当中，有两种类型的维护需求:预防性维修（事前维修）和故障维修（事后维修）。预防性维修次数过多将导致总维修成本增多，造成过维修；而预防性维修次数过少，将导致装置故障次数增多，故障维修成本也增加，并降低了装置的使用率，造成欠维修。所以，必须合理规划在有限运行时间区间内预防性维修的次数，最终达到既能使装置保持高利用率又使设备的总维修成本最少的目标。

既有的对预防性维修策略的研究主要集中在定期预防性维修上，按照事先规定的间隔时间T，当装置运行时间达到时间T就进行一次预防性维修，且假设装置“修复如新”。但这是不切实际的，因为: 1）修复往往难以达到“修复如新”的效果，大多数产品均属于劣化性质的，即随着维修次数的增多，故障率越大，即日常所说的“越修越坏”；2）对具有一定重要性装置（如国防系统）仅考虑经济性是不够的，还需考虑装置的可靠性、安全性、任务成功率等指标。

在装置的使用时间区间［0，T］内，其维修成本C主要由三部分组成:在预防性维修周期内出现的故障维修费用C1、预防性维修费用C2和因进行预防性维修而造成的损失（如生产损失、人力损失等）C3.

构建的目标函数为

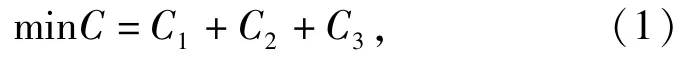
式中:

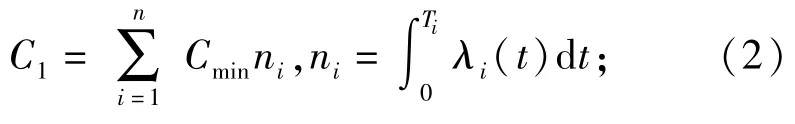
式中:ni为第i个预防性维修周期内预期发生的故障维修次数；Cmin为每次故障维修的费用；Cpm为单位预防性维修时间的费用；bi为故障率递增因子；ti为第i次预防性维修所花费的时间；Ti为第i次预防性维修周期；Cl为因预防性维修而使装置停用造成的单位时间损失。则优化模型的目标函数变为

根据前面的理论及假设，装置在不同的预防性维修周期内故障率函数不同，则其发生的故障次数也不同，所以要获得优化模型的解，必须先研究不同预防性维修周期的故障率形式。

对于劣化系统的故障率分析，Nakagawa［5］引入了故障率递增因子

式中:

则

3.2 模型的具体化

装置的寿命分布不同，则ni不同，以威布尔分布为例:，则第i次预防性维修后的故障率函数为

为了简化研究，设每次预防性维修的效果相同，即bi相同，设bi=b（i≥1），则（9）式简化为

此时优化模型的目标函数（5）式可简化为

式中:bi、ti、Ti、n为决策变量。

约束条件为

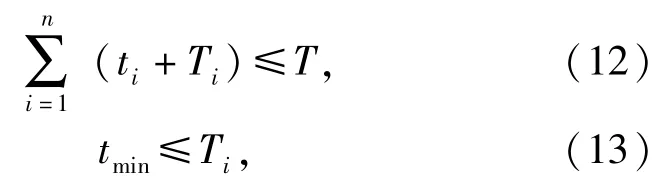
式中:tmin为预防性维修允许的最小时间。

可见，目标函数是一个非线性函数，则优化模型是一个目标函数是非线性而约束条件是线性的数学规划问题。根据数学规划的基本理论，目标函数最优解的存在性可通过函数的凹凸性来判断。

对目标函数求解时，对n取不同的数值，目标函数便变为一个非线性规划问题，可使用非线性规划求解软件lingo或Matlab编程进行求解，得到不同的总维修费用C及预防性维修周期Ti，再通过比较总维护费用大小从而确定最优的预防性维修次数n以及预防性维修周期Ti.

3.3 实例计算

某国防机械装置的故障时间符合m=2，η=75的威布尔分布，其他参数为:选取装置的使用时间为一年，即T=8 760 h；装置因预防性维修而造成的单位时间损失Cl=80万元；装置每次故障维修的费用Cmin=60万元；设装置的预防性维修时间最小为tmin= 1.5 h；预防性维修的成本函数为Cpm（bi，ti，Ti）= 200+50biTi+30ti.

假设故障率递增因子为1=b0＜b1=b2=…= bn=1.03.

将上述参数值带入目标函数，得到该机械装置使用一年的预防性维修策略的优化模型。由于模型计算量略大，在Matlab软件下对模型进行编程求解，计算结果表1所示。

由表1得知，如果装置在一年内不进行预防性维修，其总维修费用最高，可达到81.853 44万元。随着预防性维修次数n的增加，装置的总维修费用不断减少，当预防性维修次数n=16时，装置的总维修费用有极小值，当预防性维修次数继续增加，装置的总维修费用慢慢增加，装置运行若干年的总维修费用与预防性维修次数n的关系如图2所示。

从图2中的局部放大图得知，装置在有限使用时间区间内合理安排预防性维修能够有效降低装置的运行成本，则若装置运行一年中预防性维修次数小于16次，则将造成欠维修，大于16次，则造成过维修，两种情况均将增加维修费用。

装置实际使用维修中，要求维修活动花费时间越短越好，尽快使得装置恢复使用状态，实例中维修时间最短不能短于1.5 h，进行线性规划寻优，得到每次预防性维修的时间均是最短时间，符合实际情况。分析最优预防性维修次数下的各个预防性维修周期，发现呈递减的趋势，也很好地符合前文所述的劣化系统越修越坏的情况。

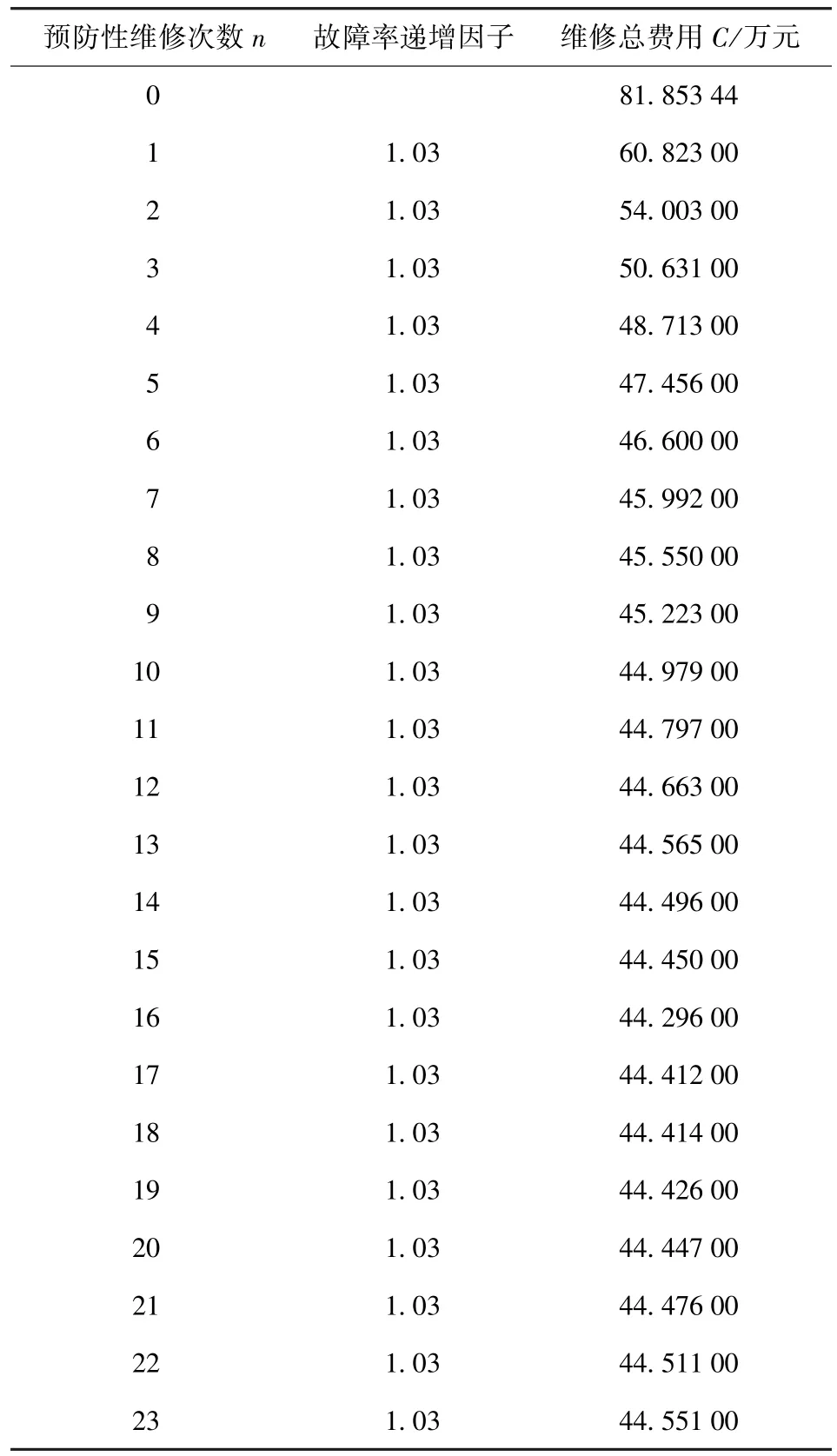
表1 预防性维修次数n及维修总费用Tab.1 Preventive maintenance frequency n and maintenance costs

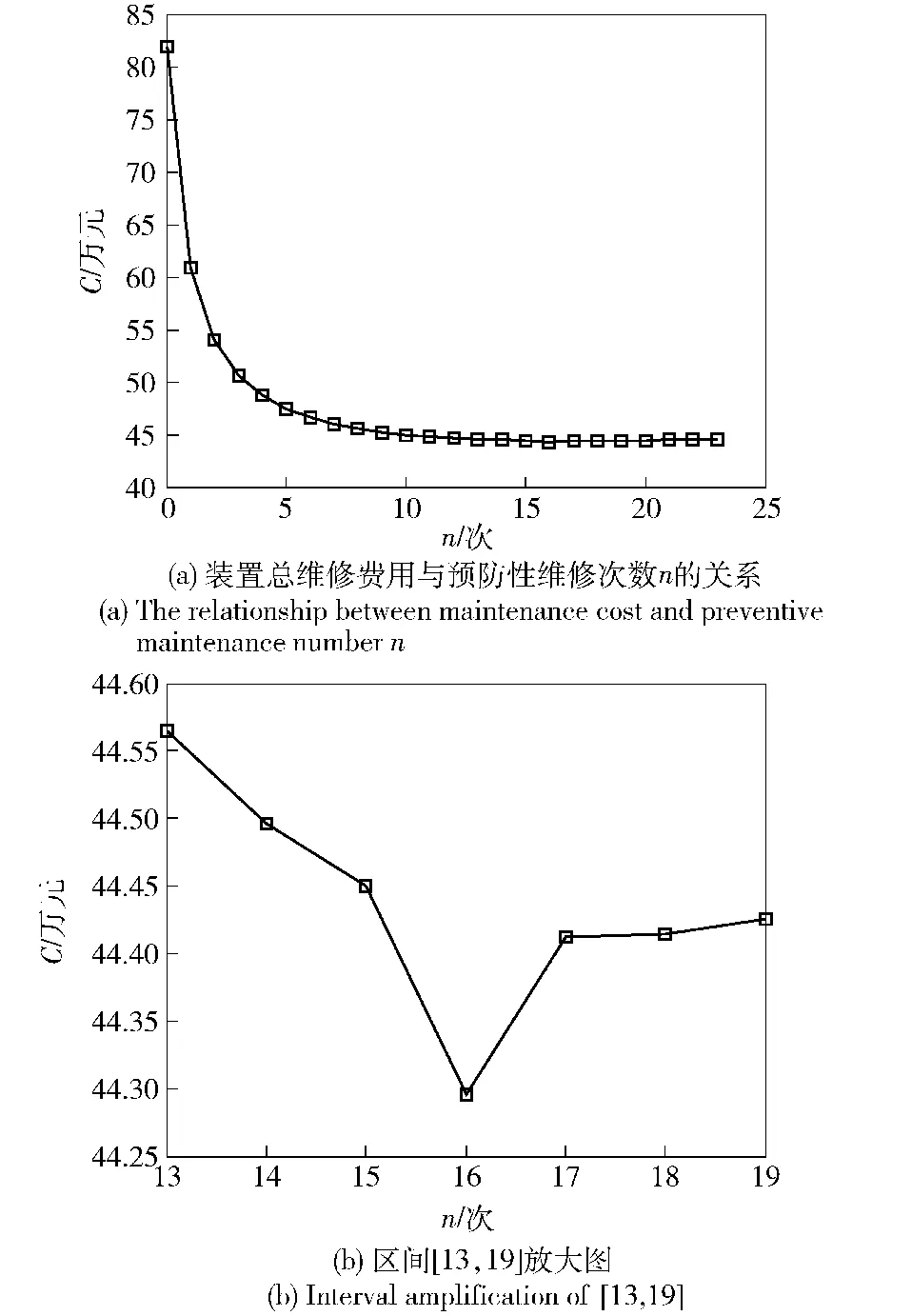
图2 预防性维修策略优化结果Fig.2 Optimization results of preventive maintenance policy

表2 n=16时各个预防性维修周期时间TiTab.2 Preventive maintenance cycle time Tifor n=16

4 考虑可靠度的优化模型

对于一些机械装置而言，除了考虑经济性以外，装置的可靠性、可用度、任务成功率等均是装置需要考虑的指标。结合以可靠性为中心的维修（RCM）理论，综合考虑装置的经济性和可靠性两个指标，对工作在有限工作时间区间内的机械装置建立优化模型。

4.1 可靠度约束

仅考虑装置的经济性而得到的最优的预防性维修次数n，可能导致第n次维修后装置剩余工作（无维修）时间过长，导致装置可靠性低，无法完成规定的任务。考虑可靠性的要求，可以在预防性维修间隔期内装备或产品保证完好率或完好数量，以满足装备作战训练或产品设备的使用要求。

为了限定装置在预防性维修周期内以及第n次维修之后的工作时间区间内的故障次数，要求装置在周期内的可靠度不得低于某一限定值，即设备的可靠度下限R0.根据产品的可靠度函数定义，可知可靠度函数在任意的时间区间内均是不增函数，所以只需满足装置在进行第i次预防性维修时装置的运行可靠度大于等于可靠度下限即可。Ri为第i个预防性维修周期内的装置运行可靠度，即需满足不等式Ri≥R0，而

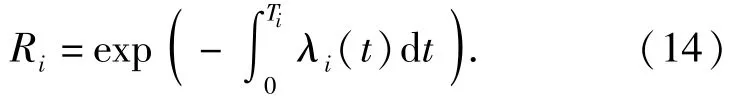
装置进行n次（最后一次）预防性维修后，其可靠度为

另外，生物教师应该多接触学生，上课提前到班，利用课间时间与学生聊聊天、开开玩笑；中午时间，与学生在办公室内聊聊天（我认为课后师生是朋友关系，不是师生关系）。在平等的关系中，缩短了彼此间的距离，学生易接受和领悟教师的一些意图，暗示效果好。教师要告诉学生，你能行，你会更好等。

为求解最少的预防性维修次数，需充分增大各预防性维修周期时间，即装置在每个预防性维修周期内均在可靠度下限下运行，可保证最大限度利用使用时间，使得预防性维修次数最少，此时

式中:λ1（t），λ2（t），…，λn（t）的计算采用（6）式即

将（17）式带入（16）式，带入具体的数值b，便可求出各预防性维修周期时间Ti，此时求得的预防性维修周期时间为装置满足可靠度要求的极限值，对应的预防性维修次数也是最少的，n为满足不等式

的最小值。

4.2 预防性维修周期的确定

按照可靠度约束所求的各预防性维修周期及最小的预防性维修次数n虽然满足可靠度要求，但从经济性的角度来看并非是最优策略［9-10］。对于优化模型，加入两个约束条件:Ri≥R0，Rl≥R0，则构成综合考虑维修费用和装置运行可靠度的优化模型，优化模型的目标函数为

约束条件为

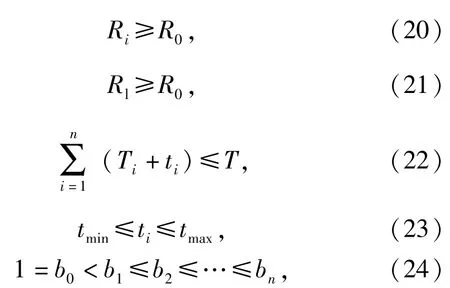
式中:ti、Ti、bi、n为决策变量。

对于优化模型，是一个非线性约束下的线性模型，因此，只要保证Cpm（bi，ti，Ti）是凸函数就可求得最优解，且对于一个确定的n，模型即转化为一个非线性规划问题，对于次数n，则有n个非线性规划。因此只需确定bi及装置的初始故障率λ（t），对n依次取不同的数值，可使用非线性规划求解软件lingo或Matlab进行优化求解，即可得到n取不同数值的总维修费用，最后再加以比较，筛选出最优的预防性维修次数以及预防性维修时间Ti.

4.3 实例计算

设某国防机械装置的寿命服从威布尔分布，参数m=2，η=100.有限运行时间为一个月，即T= 720 h，因为预防性维修占用装置而产生的单位时间损失为Cl=80万元，每次故障维修花费Cmin= 60万元，预防性维修最少需1.5 h，而且必须在1 d内完成，即tmin=1.5h，tmax=24 h.预防性维修的成本函数为Cpm（bi，ti，Ti）=200+50biTi+30ti.假设故障率递增因子1=b0＜b1=b2=…=bn=1.02.

将上述参数带入优化模型（16）式、（18）式和（19）式，得到装置在有限使用时间T=720 h的预防性维修优化模型。

1）设装置在每个预防性维修周内的可靠度下限R0=0.7.

最小预防性维修次数n通过（16）式和（18）式求得为12次，各个预防性维修周期内的最大运行时间如表3所示。

表3 仅考虑可靠度要求的n为12的预防性维修周期Tab.3 Preventive maintenance cycles only in consideration reliability for n=12

则此时计算维修费用公式

带入数据计算得到在最小维修次数为12次情况下的维修费用为C=39 271元.此时求出的维修并不是在最小维修次数n=12的最小维修费用，因为预防维修周期内以可靠度下限运行必然导致进行12次预防性维修后的装置运行可靠度过高。将n= 12带入优化模型目标函数进行规划求解，得到优化后的最小维修费用为C=37 733元，此时各预防性维修周期时间如表4所示。

表4 考虑可靠度下n为12的预防性维修周期优化时间Tab.4 The optimization times of preventive maintenance cycle in consideration of reliability for n=12

由表4发现，优化后的各预防性维修周期的运行时间表现为第1次是以最大运行时间即可靠度下限运行的，后续的预防性周期运行时间均小于最大运行时间。

2）设装置在每个预防性维修周内的可靠度下限R0=0.8.

当各预防性维修周期内的可靠度下限为0.8时，求得最小的预防性维修次数为n=15，此时装置的总维修费用C=39 424元，各个预防性维修周期内的最大运行时间如表5所示。

表5 仅考虑可靠度要求的n为15的预防性维修周期Tab.5 The preventive maintenance cycles only in consideration of reliability in consideration of reliability for n=15

将n=15及其他参数带入公式进行优化求解，解得此时总维修费用最少为C=39 182元，各个预防性维修周期时间具体如表6所示。

由表6发现，当各预防性维修周期内的可靠度下限为0.8时，优化后的各预防性维修周期的运行时间表现为前面10次均是以最大运行时间即可靠度下限运行的。

3）设装置在每个预防性维修周内的可靠度下限R0=0.9.

当各预防性维修周期内的可靠度下限为0.90时，求得最小的预防性维修次数为n=23，此时装置的总维修费用C=42 760元，各个预防性维修周期内最大运行时间如表7所示。

将n=23及其他参数带入（19）式进行优化求解，解得此时总维修费用最少为C=40 513元，各个预防性维修周期时间具体如表8所示。

表6 考虑可靠度下n为15的预防性维修周期优化时间Tab.6 The optimization times of preventive maintenance cycle in consideration of reliability for n=15

表7 仅考虑可靠度要求的n为23的预防性维修周期Tab.7 The preventive maintenance cycles only in consideration of reliability in consideration of reliability for n=23

表8 考虑可靠度下n为23的预防性维修周期优化时间Tab.8 The optimization times of preventive maintenance cycle in consideration of reliability in consideration of reliability for n=23

由表8发现，预防性维修周期可靠度下限达到0.90时，优化后的各预防性维修周期的运行时间表现为前面5次均是以最大运行时间即可靠度下限运行的。

4）设装置在每个预防性维修周内的可靠度下限R0=0.95.

当各预防性维修周期内的可靠度下限为0.95时，求得最小的预防性维修次数为n=34，此时装置的总维修费用C=460 25元，各个预防性维修周期内的最大运行时间如表9所示。

表9 仅考虑可靠度要求的n为34的预防性维修周期Tab.9 The preventive maintenance cycles only in consideration of reliability in consideration of reliability for n=34

将n=34及其他参数带入（19）式进行优化求解，解得此时总维修费用最少为C=45 810元，各个预防性维修周期时间具体如表10所示。

表10 考虑可靠度下n为34的预防性维修周期优化时间Tab.10 The optimization times of preventive maintenance cycle in consideration of reliability in consideration of reliability for n=34

分析表3～表10，不难发现，使每一预防性维修周期均以可靠度限定值运行确定的预防性维修次数及预防性维修周期并非是最优的，这是因为在有限运行时间区间内，若各预防性维修周期均是满足可靠度的最大运行时间，将导致预防性维修后剩余时间小，可靠度高，没有考虑全局，使得维修费用没有达到最优。在确定预防性维修次数后，从全局出发，综合考虑可靠性和维修成本，优化得到各预防性维修周期，使得维修费用达到最低。

图3为装置的可靠度下限与最小预防性维修次数的关系图，图4为最小维修成本与最小预防性维修次数的关系图。从图3及图4可以分析得知，增加预防性维修次数可以增大装置的可靠度，但同时也增加维修费用，当维修次数达到23后，可靠度增加缓慢，而维修费用急剧增加，造成“过维修”。而对于该装置，如果装置的可靠度允许极限值为0.9，那么此时得到较优的维修策略。

图3 可靠度下限与最小预防性维修次数的关系Fig.3 The relationship between the minimum operating reliability and number ofminimum preventive maintenance

图4 最小维修费用与最小预防性维修次数的关系Fig.4 The relationship between minimum maintenance cost and number of minimum preventive maintenance

5 结论

本文主要以有限运行时间范围内的机械装置为研究对象，用理论分析方法研究了在有限时间内预防性维修策略的优化问题，主要研究结论如下:

1）运用故障率递增因子的概念可对预防性维修与故障率间的动态变化关系进行表述。

2）对现有预防性维修成本的数学模型进行了修正，讨论了装置维护成本最低时，以及综合考虑维护成本最低及满足可靠度约束时维修次数和预防性维修周期的优化问题。只有在综合考虑维修成本及可靠度约束得到预防性维修周期才是最优的，并能够使得成本最低。

（

）

［1］ Barlow R Hunter L.Optimum preventive maintenance policies［J］. European Journal of Operational Research，1960，8（1）:90-100.

［2］ 谭林，陈童，郭波.基于几何过程的单部件可修系统最优维修策略［J］.系统工程，2008，26（6）:88-92. TAN Lin，CHEN Tong，GUO Bo.Optimal maintenance strategy for the repairable system consisting of one component based on geometric process［J］.Systems Engineering，2008，26（6）:88-92.（in Chinese）

［3］ 王冠军，张元林.维修时间受限的单部件系统几何过程维修模型［J］.东南大学学报，2013，43（6）:1335-1339. WANG Guan-jun，ZHANG Yuan-lin.Geometric process model for a single-unit system with limit repair time［J］.Journal of Southeast University，2013，43（6）:1335-1339.（in Chinese）

［4］ Malik M A K.Reliable preventive maintenance scheduling［J］. AIIE Transactions，1979，11（3）:221-228.（in Chinese）

［5］ Nakagawa T.Sequential imperfect preventive maintenance policies［J］.IEEE Transactions on Reliability，1988，37（3）:295-298.

［6］ Nakagawa T，Kowada M.Analysis of a system with minimal repair and its application to replacement policy［J］.European Journal of Operational Research，1983，12（2）:176-182.

［7］ Zhang Y L，Yam R C M，Zuo M J.A bivariate optimal replacement policy for a multistate repairable system［J］.Reliability Engineering and System Safety，2007，4（92）:535-542.

［8］ 刘晓东.装备寿命周期费用分析与控制［M］.北京:国防工业出版社，2008:1-48. LIU Xiao-dong.Material life cycle cost analysis and control［M］. Beijing:National Defense Industry Press，2008:1-48.（in Chinese）

［9］ 李果，高建民，陈富民.基于可靠性的设备维修优化方法研究［J］.中国机械工程，2007，18（4）:419-422. LI Guo，GAO Jian-min，CHEN Fu-min.Research on equipment maintenance optimization based on reliability［J］.China Mechanical Engineering，2007，18（4）:419-422.（in Chinese）

［10］ 苏春，黄茁，许映秋.基于可用度和维修成本的设备维修建模与优化［J］.中国机械工程，2007，18（9）:1096-1099. SU Chun，HUANG Zhuo，XU Ying-qiu.Modeling and optimization for device's maintenance based onallowable availability constraint and maintenance cost［J］.China Mechanical Engineering，2007，18（9）:1096-1099.（in Chinese）

Optimization Strategy of Preventive Maintenance in Finite Time Horizon

GAI Jing-bo1，KONG Yao2
（1.College of Aerospace and Civil Engineering，Harbin Engineering University，Harbin 150001，Heilongjiang，China；2.The 54th Research Institute，China Electronics Technology Group Corporation，Shijiazhuang 050081，Hebei，China）

Mechanical devices are repairable.Taking an effective preventive maintenance and reasonably arranging the preventive maintenance activities are very important to decrease the failure frequency and improve the utilization ratio.The mechanical device working in finite time horizon is studied.Maintenance cost and comprehensive consideration of maintenance cost and reliability are modeled，a nonlinear optimization software is used to solve the optimization model，and the optimal times and cycles of preventive maintenance in finite time horizon are determined.The examples show that the method of forecasting the preventive maintenance frequency and cycle is feasible.This optimization policy model can provide references for making the preventive maintenance program and predicting the service life of mechanical devices.

ordnance science and technology；preventive maintenance；maintenance strategy；optimization

TB114.3

A

1000-1093（2015）11-2164-09

10.3969/j.issn.1000-1093.2015.11.022

2014-11-18

中央高校基本科研业务费专项基金项目（HEUCF130208）

盖京波（1976—），男，副教授，硕士生导师。E-mail:gaijingbo@hrbeu.edu.cn