一种水平和垂直联合优化的3D波束成形算法

张仕宇，冯 辉，宗志远，刘 凯，杨 涛，胡 波，2

（1.复旦大学 电子工程系，上海 200433；2.复旦大学 电磁波信息科学教育部重点实验室，上海 200433）

波束成形的基本思想是通过天线阵列对发送信号进行预编码，形成多个具有不同指向性的窄带波束来动态地跟踪服务多个用户.多用户多输入多输出（Mutiluser Multiple－Input Multiple－Output，Mu－MIMO）预编码波束成形方法使得基站能够在同一频谱资源上同时服务多个用户.下行多用户传输通常建模为一个MIMO 广播信道模型，基站端采用多根天线同时服务多个用户.为了减小用户间的干扰，通常在基站端对发给各个用户的信号进行联合预编码处理.比较经典的预编码方法包括迫零（ZF）［1］，块对角化（BD）［2］，最大信漏噪比（SLNR）［3］等算法.其中，一种基于凸优化的预编码方法［4－6］能够在满足各个用户服务质量的要求下，最小化基站的发射能量.

在传统的蜂窝移动网系统中，基站往往采用的是无源天线阵列，只能选取固定的下倾角然后根据水平维度的信道信息来调整水平维度的波束方向.然而，实际的信号传播信道是具有三维空间特性的，这就使得2D 的MIMO 预编码技术并不是最优的.如果能够在三维空间上进行发射波束设计，必然能够带来更强的干扰控制能力，实现系统性能的提升.尤其是对于类似现代市区环境这样的应用场景，用户在三维空间上分布得很分散，具有可区分的俯仰角时，在水平维度和垂直维度上进行联合波束成形设计将能够更加充分地利用三维空间自由度，减小用户间干扰，提升小区的和速率（sum－rate）.

于是，3D 波束成形的概念越来越受到主流通信系统的重视.而3D 波束成形能够得以实现的一个核心技术是有源天线系统（Active Antenna System，AAS）.有源天线将射频链路（功率放大器、收发机）与天线阵元集成在一起.通过这种设计使得每个天线阵元信号的幅度、相位和时延都能够进行独立的控制［7］，从而使得更加灵活和智能的波束成形设计成为可能.而在基站端采用2D（如：面阵、L 形阵）或3D（如：球形阵）天线阵列的有源天线，便能够在水平维度与垂直维度上同时动态调整发送波束方向，即实现3D 波束成形设计.文献［8］通过实地测试表明基于AAS的自适应垂直波束成形技术能够显著提升蜂窝移动通信网络的性能.文献［9］研究了动态垂直波束在干扰避让中的应用策略.文献［10］提出了多基站根据用户位置协作调整垂直下倾角的方案.文献［11］研究了单小区MU－MIMO 场景中采用多个固定下倾角构建多个虚拟垂直小区的系统性能.文献［12］通过使用垂直预编码码本的方法来进行下倾角的动态调节.文献［13］和［14］推导了3D 信道场景下用户下倾角分布的概率密度函数，然后分别对单用户和多用户场景设计了统计最优的基站下倾角.上述文献均表明有效利用垂直维度空间自由度能够带来显著的容量提升.不过，它们仅仅只是将垂直下倾角设计作为传统水平2D 波束成形的一种补充，而没有将垂直预编码与水平预编码联合起来进行设计，因此，尚未发挥出3D 波束成形技术的最大优势.

本文针对一个基站端采用有源天线面阵的MU－MIMO 下行通信系统，将3D 波束成形问题建模成一个对水平和垂直波束成形预编码的联合设计问题，并引入一种最小化基站发射能量的优化模型.由于直接求解水平预编码和垂直预编码比较困难，于是将原问题分解成两个半定规划（Semi－Definite Programming，SDP）子问题，再通过交替迭代优化的方法逐步逼近最优的3D 波束成形预编码.仿真结果表明采用本文提出的算法得到的小区和速率性能显著优于其他对比方案.

1 系统模型

本文考虑由一个基站和K 个用户构成的单小区MU－MIMO 下行通信系统.基站离地面高度为hBS，装备有面阵天线（水平天线阵元数目为Nh，阵元间距为dh；垂直天线阵元数目为Nv，阵元间距为dv）.用户离基站的最小水平距离为Rmin，小区半径为Rmax，用户均匀分布在小区范围内.假设每个用户的高度均为hUE，并且只配备有单根天线.整个系统模型如图1所示，其中Nv＝4，Nh＝8.

1.1 有源天线阵列

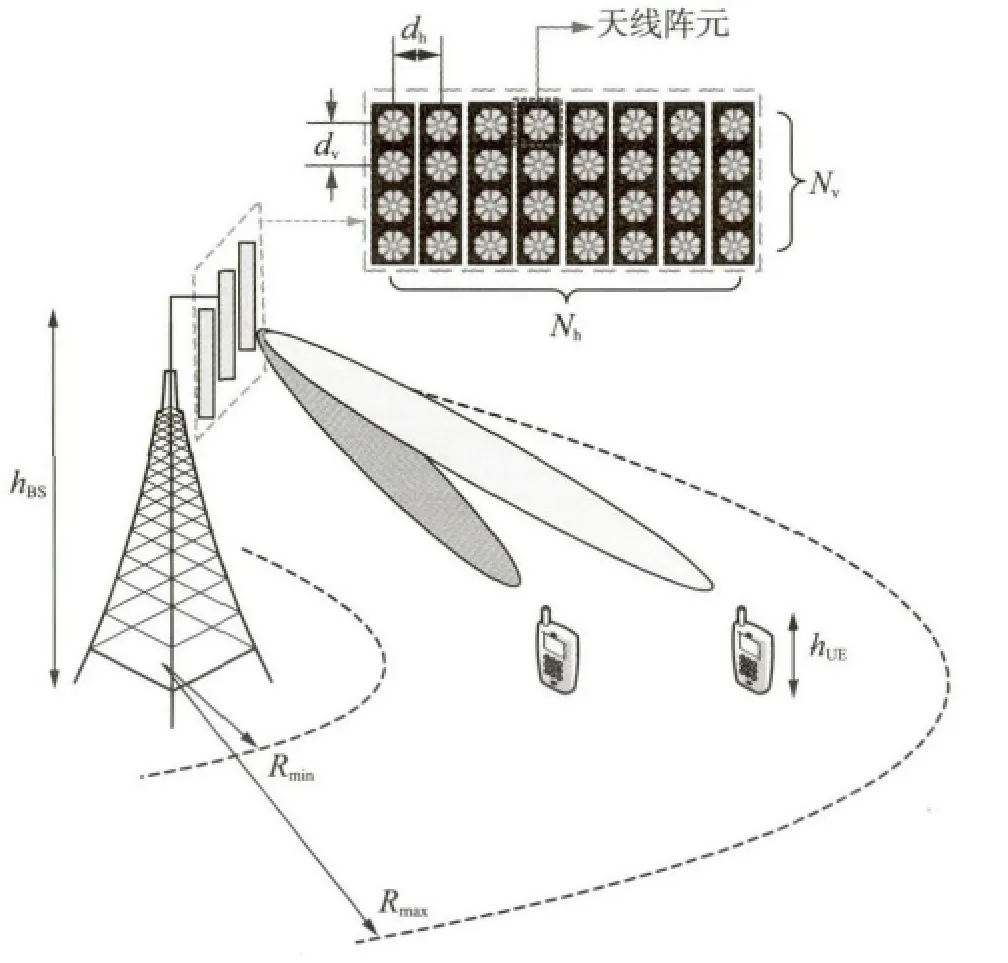
图1 3D－MIMO 通信系统Fig.1 3D－MIMO communication system

传统基站采用无源天线，在垂直维度上利用无源馈电网络激励各阵元产生振幅相同，但相位沿阵轴方向按等差数列递变的信号，从而形成固定的小区下倾角，如图2（a）所示.采用这种无源天线阵列成本低，配置简单，但是每次在垂直维度上只能产生一个波束方向.为了实现3D 波束成形，需要在垂直维度上动态调整下倾角，并能根据用户位置对不同用户的信号施加不同的相移，即产生多个下倾角不同的波束.

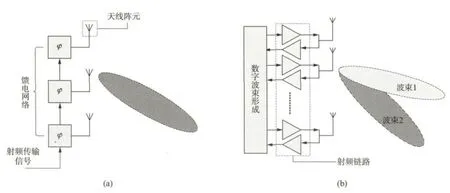
图2 （a）无源天线阵列和（b）有源天线阵列Fig.2 （a）Passive antenna array and（b）Active antenna array

因此，3D－MIMO 系统更倾向于采用有源天线技术.有源天线系统（AAS）如图2（b）所示，它将天线阵列与射频链路集成在一起，可以独立控制每个天线阵元信号的相位、幅度、时延等，从而可以实现波束在垂直维度上的动态调整以及同时多个下倾角的波束的形成［7］.

1.2 3D－MIMO信道

由于引入了垂直维度发射天线，信道系数矩阵具有三个维度，即接收天线数目Nr，基站垂直天线数目Nv和基站水平天线数目Nh.为了简化问题，本文中主要考虑用户为单接收天线的场景，因此第k 个用户的信道系数矩阵表示为Hk∈CNv×Nh.

在传统的2D－MIMO 信道建模中，往往不考虑基站和用户的高度，认为信号传播路径和环境中的各种散射体都处在同一水平面上［15］，这并不符合实际的信号传播情况.而在本文采用的3D－MIMO 信道模型中，引入了基站到用户的垂直维度的角度信息.假设基站的高度远高于传播环境中的大尺度散射体（例如房屋、树木等），而用户都贴近于地面并且被散射体环绕，并且这里不考虑散射体顶部的衍射效应.在这种假设前提下，随机散射主要发生在水平平面上（街道层级），因此认为垂直维度上的多径衰落与水平维度相比可以忽略不计.考虑窄带平坦衰落信道，基站采用Nv×Nh的面阵天线，用户为单接收天线，则用户k的信道系数可以表示为

其中，PL（dk）为路径损耗因子，采用文献［16］中的模型PL（dk）＝128.1＋37.6lg（dk），单位为dB.dk表示用户k 与基站间的距离，单位为km；表征基站到用户k之间水平维度的小尺度衰落，这里假设hk的各个元素满足独立的复高斯分布CN（0，1）.此外，e（θk）为垂直维度的信号导向矢量

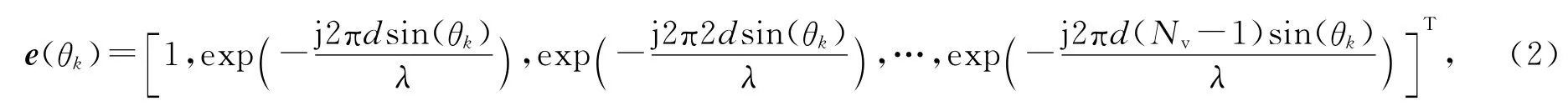
其中，θk表示从基站到用户k 的垂直维度信号离开角度（Angle of Departure，AoD）.

1.3 接收信号模型

通过这种处理可以有效降低预编码设计问题的复杂度，许多现有的3D 波束成形方案都可以归结到wk与vk的设计问题上.假设对于用户k，基站的所有天线阵元都进行服务并且只传输单层数据sk，则基站发送的信号为

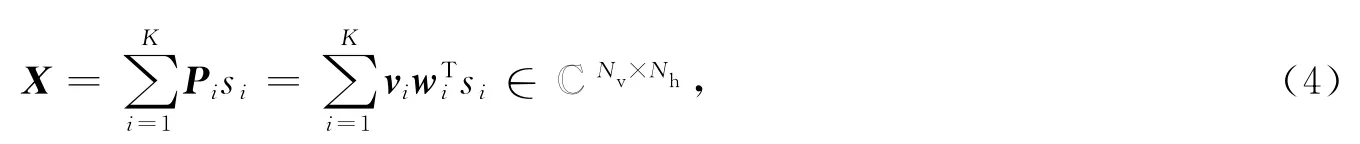
用户k接收到的信号为

其中，vec（A）表示由矩阵A 的各个列向量依次拼接而成的向量.第三个等式中第一项为有用信号，第二项为用户间干扰信号，第三项nk为噪声并假设nk～CN（0，）.于是，第k 个用户的信干噪比（Signal to Interference plus Noise Ratio，SINR）可以表示为

本文用于表征波束成形预编码性能的指标是小区用户和速率，即各个用户的传输速率之和，与各个用户的SINR 相关，其表达式如下：

2 3D 波束成形算法

本文3D 波束成形算法的最终目的是在给定基站发射功率P0的前提下，尽可能提高小区用户的和速率.优化问题如下所示：

由于优化问题（8）中wk与vk耦合在一起，且优化目标形式复杂，该问题非凸，求解十分困难.同时，文献［18］也证明了，一般的给定发射功率的最大和速率波束成形优化问题是一个NP难题.下面本文介绍一种将原问题分解为分别关于wk与vk的最小发射能量优化子问题，并通过迭代逼近求解的方法.

2.1 优化子问题设计

在本节中，原问题被转换为最小化功率设计问题，并分解为分别关于垂直预编码和水平预编码的优化子问题进行求解.

由于一般的给定功率最大和速率波束成形优化问题求解十分困难，下面考虑一种在保证每个用户的SINR 最低门限的前提下，最小化基站的总发射功率的波束成形设计思想［4］.针对本文的3D－MIMO 场景，该优化模型可以表述为

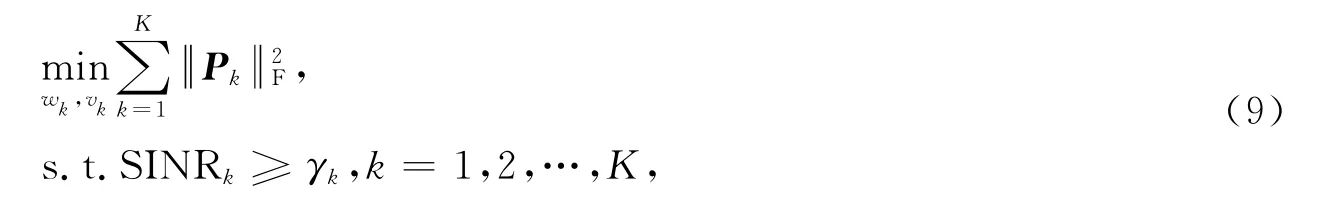
其中，γk为用户k 的SINR 门限.文献［5］证明了当γk，k＝1，2，…，K 选取合适时，最小发射能量问题（9）的解同时也是最大和速率问题（8）的解，因此从（8）到（9）的转换是合理的.然而，我们很难预先知道合适的SINR 门限值是多少.下一节将介绍一种通过迭代求解优化问题（9）并不断提升SINR 门限的方法来逼近优化问题（8）的解.本小节将专注于优化问题（9）的求解方法.

由于优化问题（9）中wk与vk耦合在一起，问题非凸，求解困难.下面考虑将其分解为关于垂直预编码和水平预编码的优化子问题进行求解.首先介绍一条关于面阵发射预编码总功率的引理.

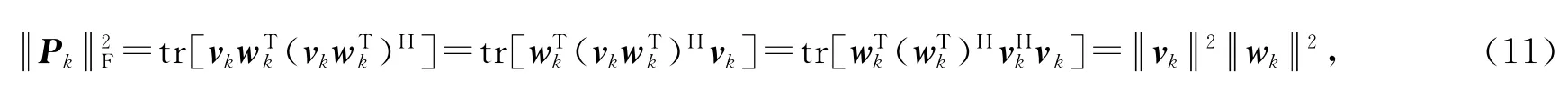
其中tr（A）表示矩阵A 的迹，第二个等号运用了迹的性质tr（AB）＝tr（BA）.

根据引理1，发射总功率优化目标可以表示为

于是考虑在求解原问题（9）时，采用一种交替迭代的思想（类似文献［19］），即先将vk固定，优化求解wk，然后根据求得的wk再来优化求解vk，如此反复交替迭代求解vk和wk.下面给出当vk和wk分别已知时的两个优化子问题：

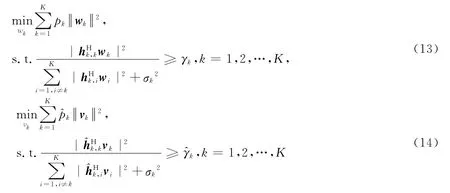
其中，pk＝分别表示第k个用户垂直和水平预编码的发送能量，hk，i＝表示基站到用户k的信道矩阵Hk经过垂直预编码vi后得到的等效水平信道系数；表示基站到用户k的信道矩阵Hk经过水平预编码wi后得到的等效垂直信道系数.

接下来采用半定松弛（Semi－Definite Relaxation，SDR）［6］方法求解这两个优化子问题.

以求解水平预编码为例，当vk固定时，优化问题（13）可以归结为经典的加权能量优化波束成形设计问题［5］.定义矩阵，优化问题（13）可以转换为

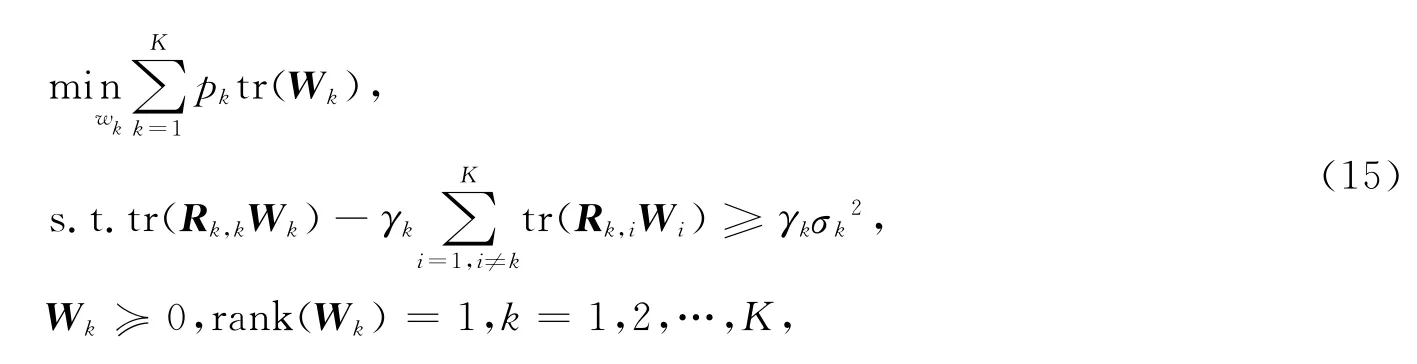
其中，A≿0表示矩阵A 是半正定的，rank（A）表示矩阵A 的秩.当舍弃限制条件rank（Wk）＝1时，优化问题（15）可以转化为一个松弛的半定规划问题［6］，继而可以利用凸优化工具包CVX［20］进行快速求解.同理，在wk给定时，对于优化问题（14），可以采用同样的方法松弛求解.因此，可以通过交替迭代优化wk和vk来实现水平和垂直预编码的联合优化设计.

2.2 迭代逼近算法

根据上一节的说明可知，只有当γk，k＝1，2，…，K 选取合适时，最小发射能量问题（9）的解才与最大和速率问题（8）的解相同.否则在保证初始SINR 门限在P0功率限制下可达到的前提下，通过优化问题（9）求解出的预编码功率往往小于功率P0，并没有充分利用给定的发射功率，进而导致系统和速率无法达到最大.此时，若对求解出的预编码进行等比例放大，使其功率等于P0，则用户SINR 能够进一步提升.于是，本文希望通过迭代求解最小发射能量问题，并不断提升SINR 门限的方法来逼近最大和速率问题的解.下面给出对具体的迭代逼近过程的描述.

同样以水平预编码wk设计问题为例（假定vk已知，其功率为pk，k＝1，2，…，K），首先给定基站发射功率P0，并选取合适的初始用户SINR 门限γk，k＝1，2，…，K，注意该门限需要保证在预编码功率不大于P0的前提下是能够达到的.然后通过前述的SDR 方法求解最小发射功率问题（13），记最优解为，k＝1，2，…，K.容易知道采用时的发射总功率将小于设定的基站发射功率P0，即.根据文献［5］，在最优解处，最小发射功率问题（13）的约束条件必然取等号，即

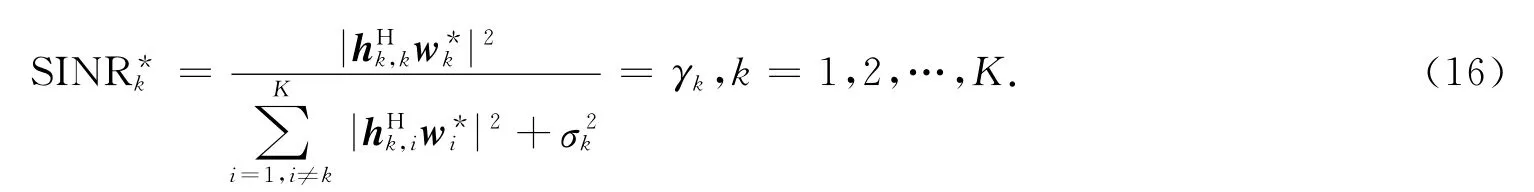
然后，将各个用户的预编码等比例放大得到新预编码w′k，使得w′k的功率等于P0，即w′k＝μw＊k，其中μ为放大系数，满足μ ＝.于是根据新预编码得到的用户SINR 满足

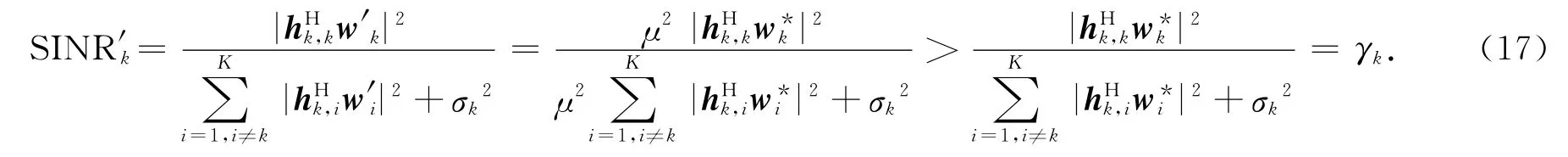
虽然在本节中描述的只是针对求解wk的迭代逼近方法，但是迭代提升门限的方法在wk与vk的交替迭代求解过程中也同样适用，具体的算法步骤将在下一节中说明.

2.3 交替迭代算法步骤

结合前述的子问题设计和迭代逼近方法，表1列出了本文提出的交替迭代优化算法的详细步骤，其中分别表示第m 次迭代时的水平预编码和垂直预编码，分别表示第m 次迭代时，对应于子优化问题（13）和（14）的SINR 门限.

下面对算法的收敛性进行说明：在每次算法迭代的第2步和第4步的优化目标都是基站端的总发射功率，所以每轮迭代得到的发射预编码功率总小于或等于初始功率P0；而在第3步和第5步中，将预编码功率放大至P0，计算并更新优化限制中的SINR 门限（提高SINR 门限），使得各个用户的SINR 随着迭代的进行不断提高，在发射功率有限的前提下最终将收敛.

表1 交替迭代优化算法流程Tab.1 Alternating iterative optimization algorithm

3 仿真结果分析

本节将通过蒙特卡洛方法对本文提出的迭代优化算法的性能进行仿真验证和分析.

3.1 小区参数配置

小区的基本配置情况：基站天线高度hBS＝25m，用户天线高度hUE＝1.5m，用户与基站最小水平距离Rmin＝10m，小区半径Rmax＝250m，基站水平天线数目Nh＝8，基站垂直天线数目Nv＝1，2，4或8，路径损耗模型［16］PL（d）＝128.1＋37.6lg（d），其中d 为基站到用户的距离.每次仿真时，用户随机均匀地分布在小区服务范围内，进而根据用户的位置按照1.2节中的方法生成信道.同时，假设基站发射天线采用有源面阵天线，天线阵元间距为dv＝dh＝λ／2，其中λ表示载波波长.

3.2 对比方案设计

在进行3D 波束成形设计时，现有的许多研究［9－14］常常把水平维度与垂直维度的预编码设计完全独立开来.水平维度预编码设计与基于等效水平MIMO 信道的传统波束成形设计问题一样，采用包括迫零（ZF）［1］、块对角化（BD）［2］、最小发射能量［4－6］等算法.而在垂直维度上，可以考虑以下两种简单的垂直预编码策略.

1）固定下倾角（Cell－Fixed）

传统蜂窝移动网络中基站端通常采用图2（a）所示的无源天线阵列作为一个水平的天线端口（Antenna Port），使得发送信号具有一个固定的下倾角.通常该下倾角需要根据小区实际情况进行确定，使得某些小区统计性能指标达到最优.不失一般性，这里让发射波束在垂直维度上指向小区中心，即取发射下倾角为

则此时各个用户的垂直预编码固定为

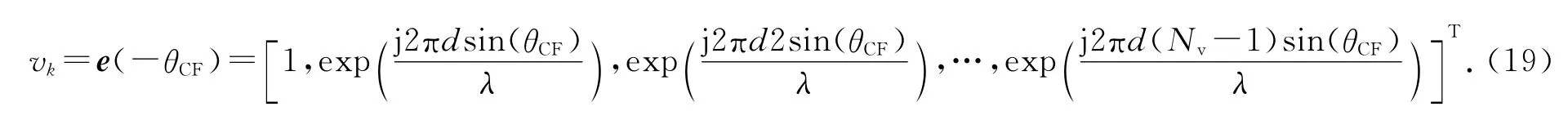
2）指向用户（User－Specific）［21］

根据有源天线的特性，对于每个用户可以采用不同的垂直预编码，产生多个波束分别指向各个用户，使得每个用户的接收信号功率达到最大，此时用户的垂直预编码为

这种方法试图最大化用户接收到的有用信号的功率，却没有考虑用户之间干扰的影响.下面将各种垂直预编码策略与水平预编码算法进行组合，提出4种简单的3D 波束成形方案，如表2所示.本文将以它们作为基准，在仿真过程中与前面提出的迭代优化算法进行性能对比.

其中，方案1和方案3对应于传统的无源天线阵列基站，垂直维度上采用固定下倾角，只在水平维度上进行波束成形设计；方案2和方案4对应于有源天线阵列基站，但是在垂直维度上只是简单地将波束方向指向用户，最大用户接收有用信号功率.

表2 3D波束成形对比方案Tab.2 The comparison scheme for 3Dbeamforming

3.3 仿真结果及分析

下面比较了不同3D 波束成形方案在8用户下行场景下的小区和速率性能，基站天线采用4×8面阵，用户端均为单接收天线，设定迭代交替算法的收敛判决因子为τ＝10－3.这里，定义边缘信噪比（Edge SNR）为不考虑信道小尺度衰落影响时的小区边缘处信噪比，即SNREdge＝

图3显示了不同3D 波束成形方案下小区和速率与边缘SNR 之间的关系，从图中可以看出，在垂直维度上指向用户的预编码方案较之固定下倾角方案具有5%～6%的和速率提升，说明利用垂直空间的自由度确实能够有效提升系统性能.同时，本文提出的迭代优化算法在2dB 边缘信噪比条件下，较之传统块对角化方案（Scheme 1、Scheme 2）分别有39%和31%的性能提升，较之最小发射能量优化方案（Scheme 3、Scheme 4）也分别有10%和5%的性能提升.

图4给出了基站采用不同数目的垂直维度天线情况下，8用户小区下行和速率情况（对应2 dB边缘信噪比条件）.随着垂直维度天线数目的增加，基站在垂直维度上的空间分辨率增大，指向用户的垂直预编码方案相对于传统固定下倾角系统性能提升越发显著，并且逐渐逼近交替迭代优化算法性能.当天线数目趋向无穷大时，垂直维度波束将能够完全区分用户，不存在用户间干扰，指向用户的垂直预编码算法性能将达到最优.然而实际应用中，天线数目有限，且很难准确得到用户下倾角.相较而言，本文提出的交替迭代算法不需要知道用户下倾角，根据信道状态信息能够自适应地将波束对准用户，收敛到一个较优的解.

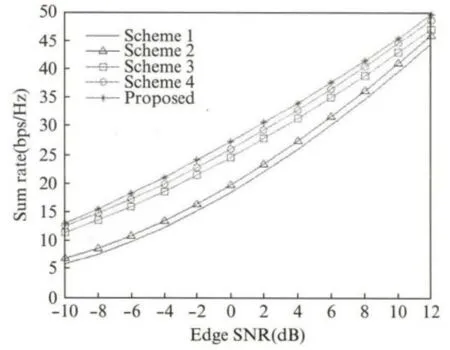
图3 不同3D 波束成形方案性能Fig.3 The performance of different 3D beamforming schemes

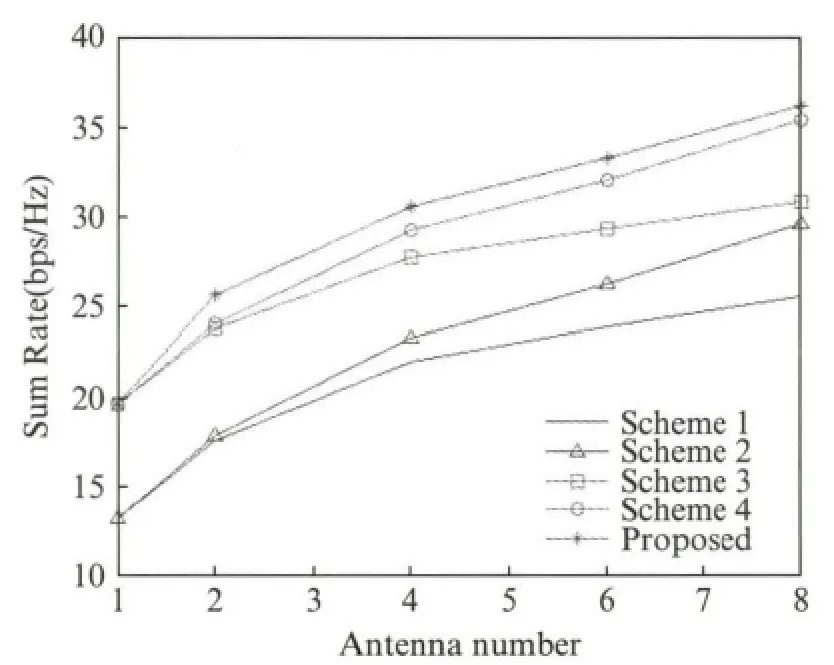
图4 不同垂直天线数目下的系统性能Fig.4 The system performance with different vertical antenna numbers

本文提出的3D 波束成形算法通过交替迭代逐步逼近一个较优的波束预编码的解.在迭代过程中，基站发射功率保持不变，用户SINR 门限不断提升，保证最终算法能够收敛.图5展示了算法的收敛过程，可以看到在2～3次迭代后算法即可收敛，但随着天线数目的增多收敛速度会减慢.

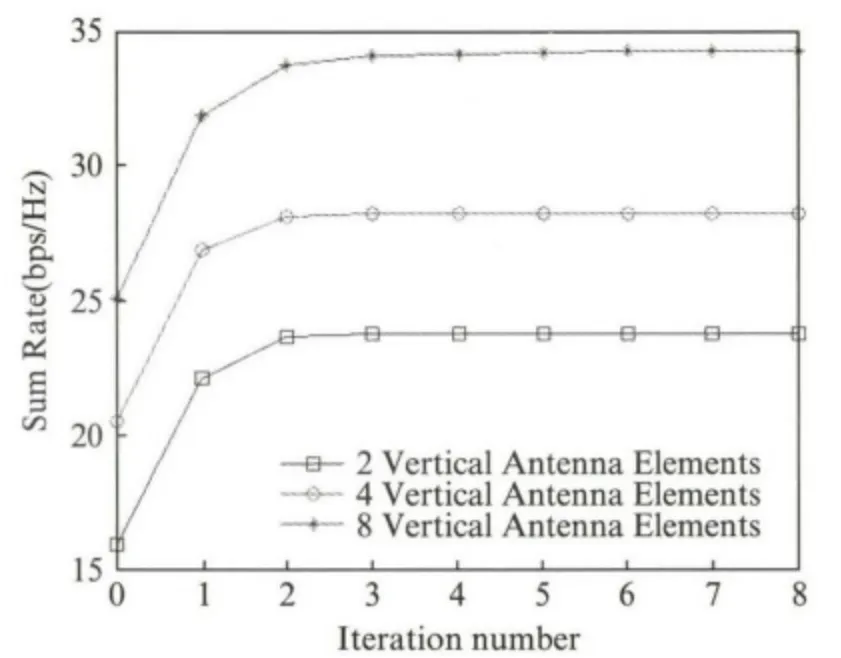
图5 交替迭代优化算法收敛速度Fig.5 The convergence rate of the alternating iterative optimization algorithm

图6给出了基站垂直维度天线分别为4天线和8天线条件下，采用交替迭代算法得到的收敛后的垂直维度波束图.仿真场景为两用户，用户下倾角分别为20°和30°，迭代初始时给定各个用户的垂直预编码能量相同且波束方向均指向小区中心.可以看到，在迭代优化过程中，算法在垂直维度上进行了两步操作：（1）调整波束方向自适应地指向用户；（2）在用户间进行功率分配，离基站越远，路径损耗越大，分配的能量越多.

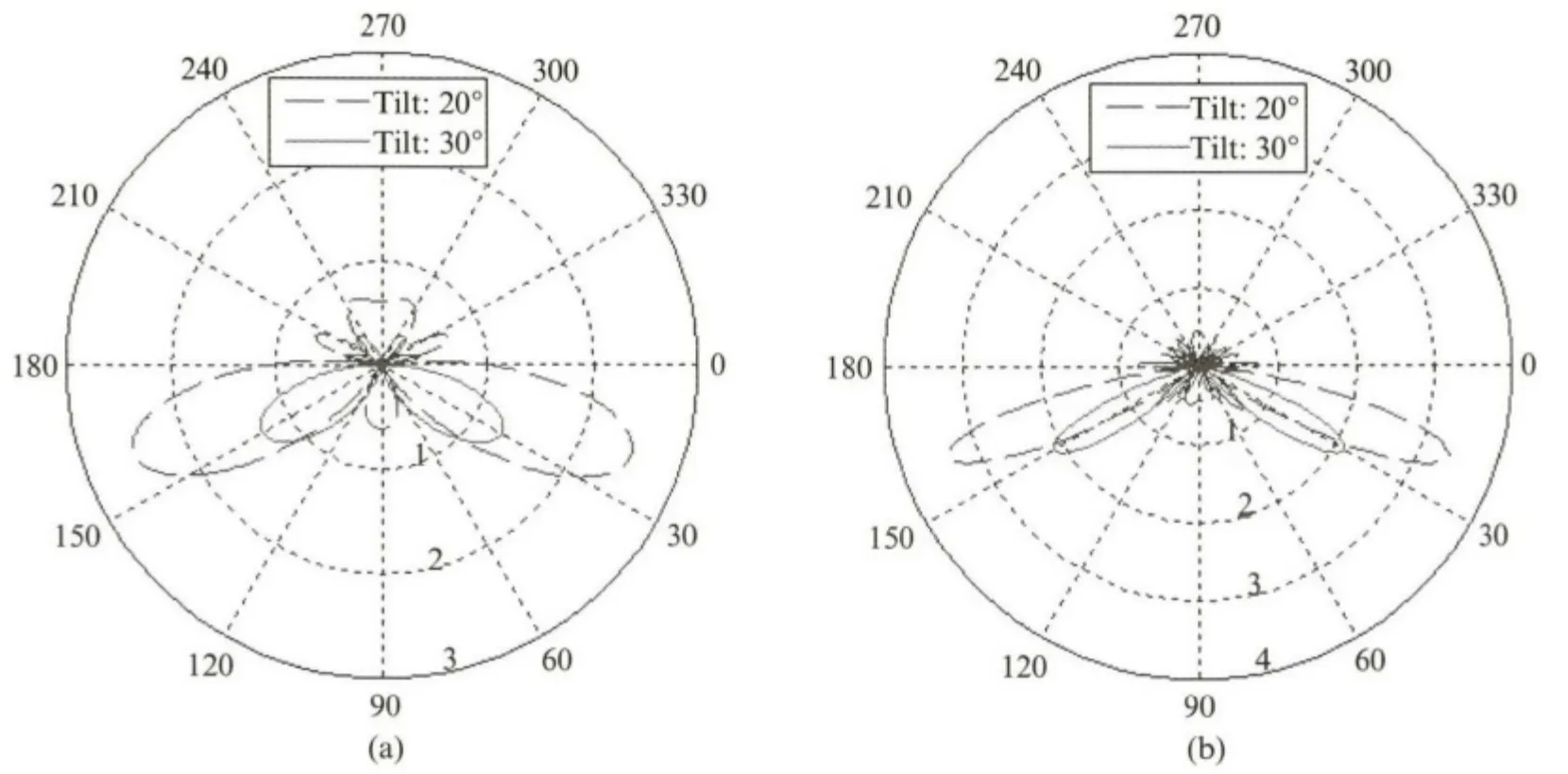
图6 （a）垂直维度4天线波束方向图，（b）垂直维度8天线波束方向图Fig.6 The beam pattern in vertical plane with（a）4vertical antennas and（b）8vertical antennas

4 总结

本文针对3D－MIMO 场景，对有源面阵天线的3D 波束成形问题进行建模，将其抽象为对天线阵列水平预编码和垂直预编码的联合设计问题.该问题可以进一步分解为两个分别设计水平和垂直预编码的优化子问题，并通过半定松弛（SDR）和交替迭代的方法进行求解.仿真结果证明该算法能够很快收敛，而采用该算法得到的小区和速率明显高于固定下倾角方案和直接将波束指向用户的方案.本算法无需事先知道用户的下倾角，而是能够依据信道状态信息自适应地调整波束指向用户并进行用户间功率分配.基于本文的研究，未来可以进一步研究非完全信道状态信息反馈时的3D 波束成形算法，并将其扩展到多小区协作的场景中.

［1］Wiesel A，Eldar Y，Shamai S.Zero－forcing precoding and generalized inverses［J］.IEEE Transactions on Signal Processing，2008，56（9）：4409－4418.

［2］Spencer Q H，Swindlehurst A L，Haardt M.Zero－forcing methods for downlink spatial multiplexing in multiuser MIMO channels［J］.IEEE Transactions on Signal Processing，2004，52（2）：461－471.

［3］Sadek M，Tarighat A，Sayed A H.A leakage－based precoding scheme for downlink multi－user MIMO channels［J］.IEEE Transactions on Wireless Communications，2007，6（5）：1711－1721.

［4］Gershman A B，Sidiropoulos N D，ShahbazPanahi S，et al.Convex optimization－based beamforming［J］.IEEE Signal Processing Magazine，2010，27（3）：62－75.

［5］Bjornson E，Bengtsson M，Ottersten B.Optimal multiuser transmit beamforming：A difficult problem with a simple solution structure［J］.IEEE Signal Processing Magazine，2014，31（4）：142－148.

［6］Luo Z Q，Ma W K，Ye Y Y，et al.Semidefinite relaxation of quadratic optimization problems［J］.IEEE Signal Processing Magazine，2010，27（3）：20－34.

［7］Linehan K，Chandrasekaran R.Active antennas：The next step in radio and antenna evolution［EB／OL］.［2014－09－01］.http：∥docs.commscope.com／Public／active＿antenna＿system＿white＿paper.pdf.

［8］Koppenborg J，Halbauer H，Saur S，et al.3Dbeamforming trials with an active antenna array［C］∥International ITG Workshop on Smart Antennas.Dresden，Germany：IEEE Press，2012：110－114.

［9］Halbauer H，Saur S，Koppenborg J，et al.Interference avoidance with dynamic vertical beamsteering in real deployments［C］∥IEEE Wireless Communications and Networking Conference Workshops.Paris，France：IEEE Press，2012：294－299.

［10］Seifi N，Coldrey M，Viberg M.Throughput optimization for MISO interference channels via coordinated user－specific tilting［J］.IEEE Communications Letters，2012，16（8）：1248－1251.

［11］Seifi N，Coldrey M，Svensson T.Throughput optimization in MU－MIMO systems via exploiting BS antenna tilt［C］∥IEEE Globecom Workshops.Anaheim，CA，USA：IEEE Press，2012：653－657.

［12］Hoshino K，Fujii T.Improving throughput by multi－cell coordinated vertical plane beam control with precoding［C］∥IEEE Vehicular Technology Conference.Yokohama，Japan：IEEE Press，2012：1－5.

［13］Lee W，Lee S R，Kong H B，et al.3Dbeamforming designs for single user MISO systems［C］∥IEEE Global Communications Conference.Atlanta GA，USA：IEEE Press，2013：3914－3919.

［14］Lee W，Lee S R，Kong H B，et al.Downlink vertical beamforming designs for active antenna systems［J］.IEEE Transactions on Communications，2014，62（6）：1897－1907.

［15］3GPP TR 25.996 V11.0.0.Spatial channel model for Multiple Input Multiple Output（MIMO）simulations［R］.Sophia Antipolis：3GPP，2012.

［16］3GPP TR 36.814 V9.0.0.Further advancements for E－UTRA physical layer aspects［R］.Sophia Antipolis：3GPP，2010.

［17］Li Y，Ji X D，Peng M G，et al.An enhanced beamforming algorithm for three dimensional MIMO in LTE－advanced networks［C］∥International Conference on Wireless Communications ＆Signal Processing.Hangzhou，China：IEEE Press，2013：1－5.

［18］Liu Y F，Dai Y H，Luo Z Q.Coordinated Beamforming for MISO interference channel：Complexity analysis and efficient algorithms［J］.IEEE Transactions on Signal Processing，2011，59（3）：1142－1157.

［19］Serbetli S，Yener A.Transceiver optimization for multiuser MIMO systems［J］.IEEE Transactions on Signal Processing，2004，52（1）：214－226.

［20］Grant M，Boyd S，Ye Y.CVX：Matlab software for disciplined convex programming［OL］.（2009－01－01）.［2015－01－01］.http：∥www.stanford.edu／～boyd／cvx.

［21］Halbauer H，Saur S，Koppenborg J，et al.3D beamforming：Performance improvement for cellular networks［J］.Bell Labs Technical Journal，2013，18（2）：37－56.