一类常微分方程的BDF－凹凸分离数值格式

李伟嘉，韩亦童，严 阅

（复旦大学 数学科学学院，上海 200433）

1 介 绍

这里定义所谓的“能量”函数：

和对应的常微分方程：

容易验证，这个常微分方程的解满足

这里常数C 由初值u0确定.如果在方程（2）两边乘以，并从t1到t2积分，即

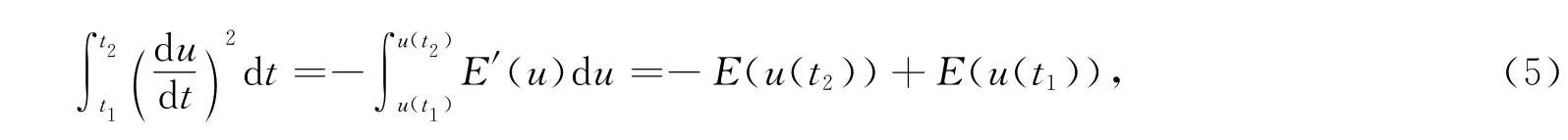
那么有所谓的“能量”稳定性：

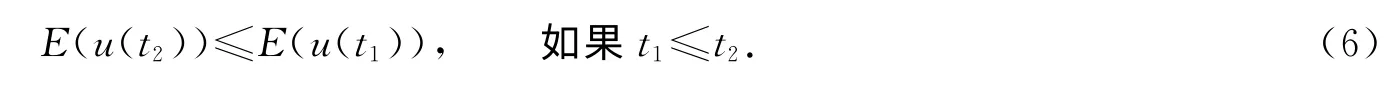
如果考虑长时间计算的问题，也就是T 足够大，可以考虑作尺度变换t→，从而可以考虑在［0，1］上带小参数ε的问题：容易验证uε（t）＝

如图1所示，u（t）＝0是方程的不稳定平衡点，u（t）＝±1是方程的两个稳定平衡点.当t→＋∞时，对于任意给定的u0，当u0＞0时，u（t）→1；u0＜0时，u（t）→－1.而且当ε越小，uε会变得越陡，求解的问题变得刚性和困难.因此稳定的数值方法非常重要.

上述这类方程的特点是有比较弱的（线性）增长项，另外有比较强的（三次）非线性控制项.当初值比较小的时候，即｜u0｜≪1，解随着时间会指数增长，由于有非线性项的控制作用，增长速度单调下降趋于0，解也趋于稳定.相反，当初值比较大的时候，即｜u0｜≥1，解随着时间会指数衰减，由于有线性项的增长作用，衰减速度单调下降趋于0，解同样趋于稳定.

在数值计算上，显然如果用最简单的显式Euler格式（或其他的显式格式）是不适合的，为了计算稳定，时间步长要选取的非常小，特别是对刚性问题（或小ε）的情况；另一方面，如果用隐式格式，会需要面临代数方程的根不唯一的问题［1－2］.最近在研究薄膜外延生长（Molecular Beam Epitaxy，MBE）模型的数值方法过程［3－11］中，Eyre的凹凸分离的方法［12］被进行了深入的研究和分析，并被推广应用到Darcy－Stokes流［13］、Cahn－Hilliard模型［14］、相场晶体模型［15］和带指数非线性项的波方程［16］等.凹凸分离的基本思想是在能量泛函中，把能量分解为凸项和凹项的组合，对凸能量项用隐式格式处理，对凹能量项用显式处理，这样构造的格式具有能量稳定、求解非线性代数方程解唯一等优点，但是这个方法对于如何构造两阶或更高阶的格式到现在为止只有少量的工作.本文回到最基本的常微分方程，结合常微分方程经典的Gear格式（BDF格式）和凹凸分离思想来构造计算格式.BDF格式是一类对刚性问题非常有效的典型的数值格式［1－2］，这里我们修改BDF格式，通过对能量函数中的凹项作显式或外推处理，对凸项直接用隐式处理.本文给出了相应的稳定性和收敛性分析，并把这个格式用于求解Allen－Cahn方程，数值结果表明这个格式和想法对于求解非线性偏微分方程（Partial Differential Equation，PDE）也是有效的.

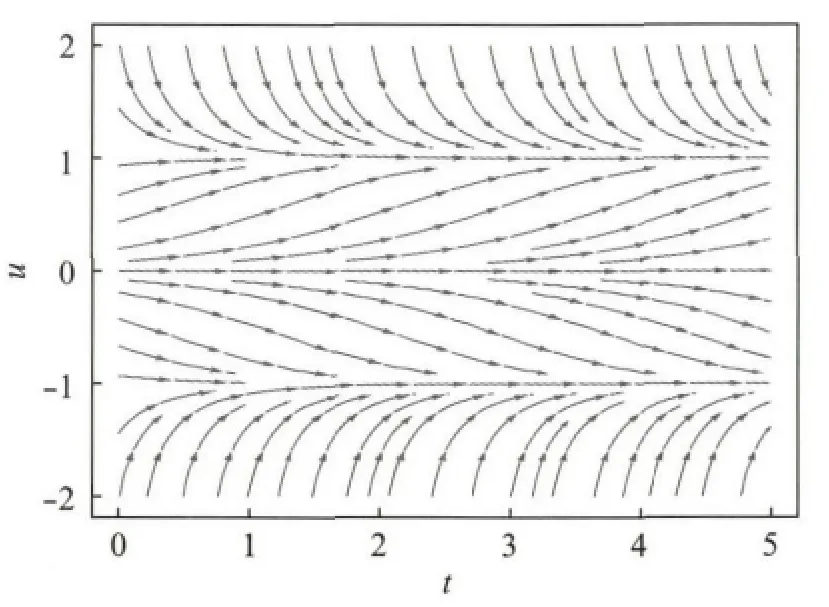
图1 常微分方程解的示意图Fig.1 Sketch map of solutions to the ordinary differential equations

2 两个凹凸分离的数值格式

按照凹凸分离的思想，考虑方程（2）的数值格式.设N 是正整数，0＝t0＜t1＜…＜tN＝T 是［0，T］上的均匀剖分，τi＝ti－ti－1，i＝1，2…，N，为方便起见我们假设步长是等步长的，也就是τ＝τi＝.对于该问题，能量函数（1）可以分解为两个凸函数的组合，即

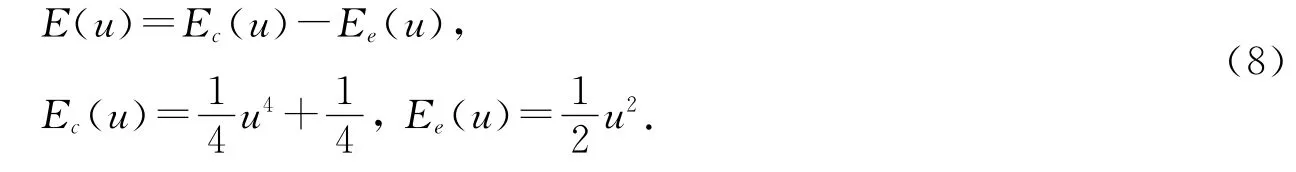
注意到这种凹凸的分解是不唯一的.根据经典的凹凸分离格式的构造方法，我们将E′c（u）处理为隐式项，处理为显式项，构造如下一阶和二阶数值格式：

1）一阶格式

2）二阶格式

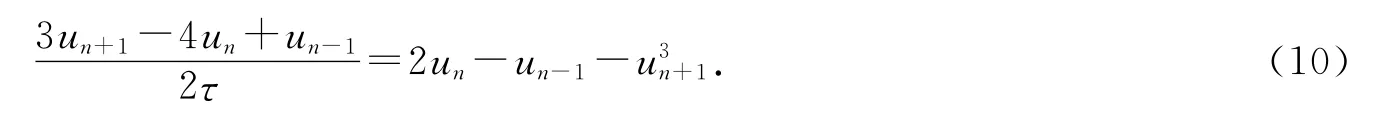
这里un为tn时刻的计算解.在上述两个格式中，我们基于Gear格式（BDF 格式）来尽可能得到大的绝对稳定区域，同时结合外推来处理显式项（Adams格式）使得整体精度一致.这个格式在文献中也称为IMEX（IMplicit－EXplicit）隐显格式.在常见的IMEX 格式中通常是线性项隐式处理，非线性项显式处理来使得计算方便.这里我们对非线性项用隐式处理，线性项显式处理是为了稳定性考虑，特别是长时间稳定性.当然，在每步的计算过程中，还需要求解一个非线性代数问题，由于隐式部分是严格凸函数的导数，所以像牛顿方法、非线性共轭梯度方法等都有好的结果.特别是对我们的例子，三次方程可以有解表达式，而且解是唯一的，对整体计算量增加不大.

为方便起见，我们引入几个差分记号δ，δ2和D：

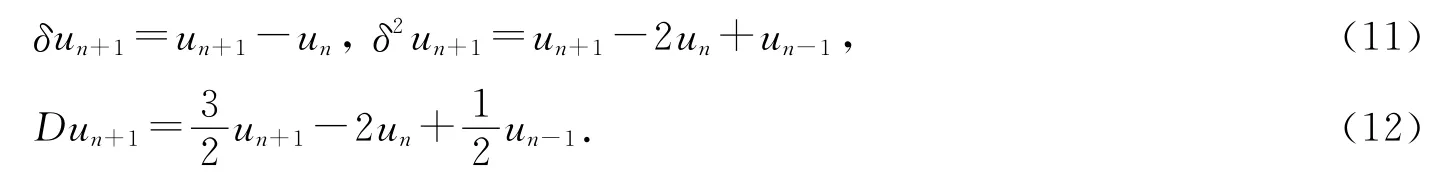
3 稳定性分析

在这一节我们将证明上述两个计算格式（9），（10）是适定的，且能量稳定的.

定理1 求解方程（2）的格式（9）是适定的，并且保持能量递减性和数值解的有界性，即

证 对于格式（9），设

则f（u）的原函数

由于

因此F（u）为凸函数，而且严格凸的，所以格式（9）唯一可解.然后，在一阶格式（9）两端同乘以δun＋1，则

由于Ec（u）和Ee（u）都是凸函数，故有下列不等式成立：

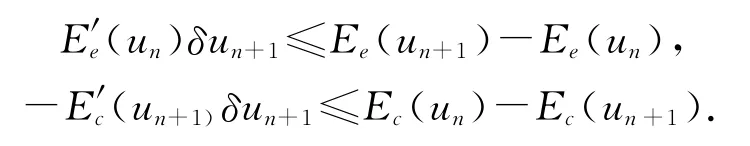
因此，

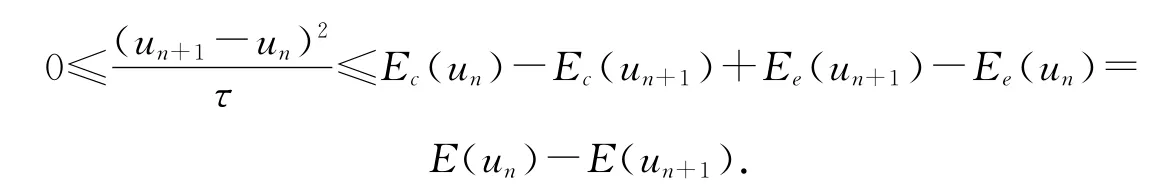
所以能量递减性成立：

由E（u）定义，易知

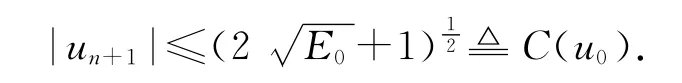
从而解的有界性成立.

定理2 求解方程（2）的格式（10）是适定的，并且在数值能量函数

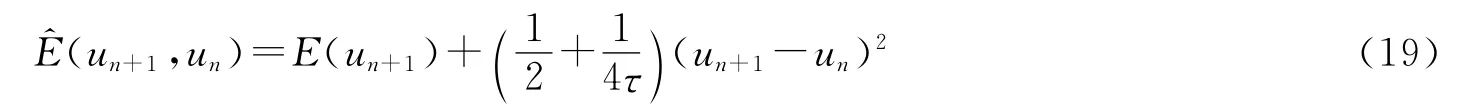
下，如果满足τ≤2，则保持能量递减性和数值解的有界性，即

证 仿照定理1证明，易知格式满足唯一可解性.在格式（10）两端同乘以δun＋1，则

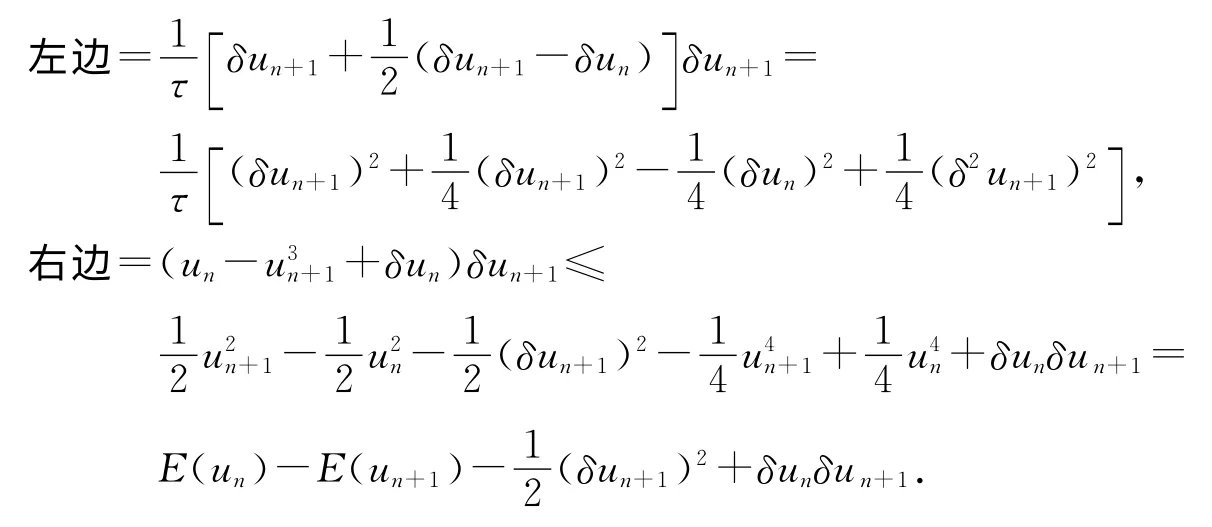
结合上述两式，并由数值能量定义（19）式和条件τ≤2，有

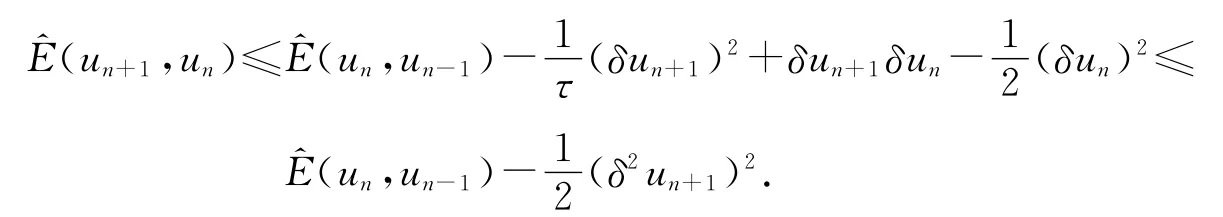
从而得到数值能量的单调递减性.

再由递推关系式

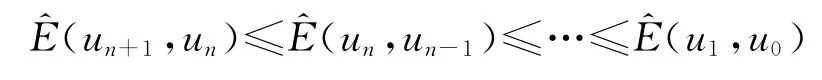
和数值能量的定义（19）式得到

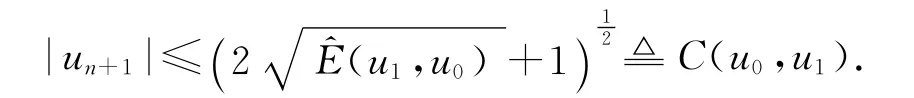
从而解的有界性成立.

注1 上述定理成立需要满足条件τ≤2，如果在格式左边加入稳定项τ（un＋1－un），使之变为新二阶格式

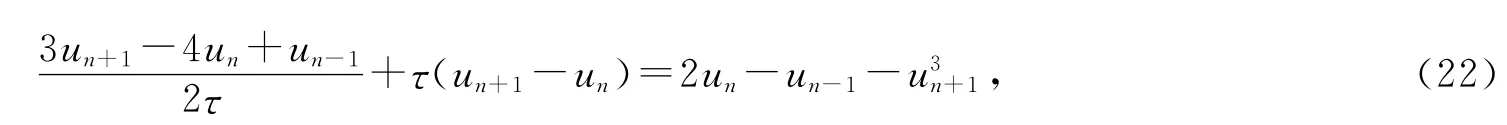
则新二阶格式解除了对时间步长τ的限制，无条件满足能量递减性.

4 收敛性

这里我们将证明格式（9）是一阶收敛的，而格式（10）是两阶收敛的.定义tn时刻的误差为

在证明过程中，需要下面基本的不等式（引理1）和Gronwall不等式（引理2），证明分别见文献［6］和［17］.

引理1［6］对任意的向量a，b∈Rn，都成立

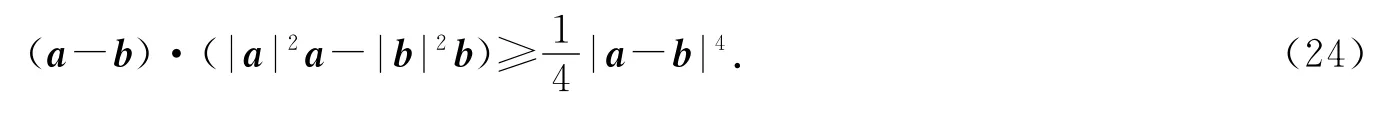
引理2［17］对于固定的T，假设是非负序列，满足≤C1，其中C1不依赖于τ，N，Nτ＝T，如果∀τ＞0，满足

其中C2＞0是不依赖于τ和N 的常数.那么∀τ＞0，有

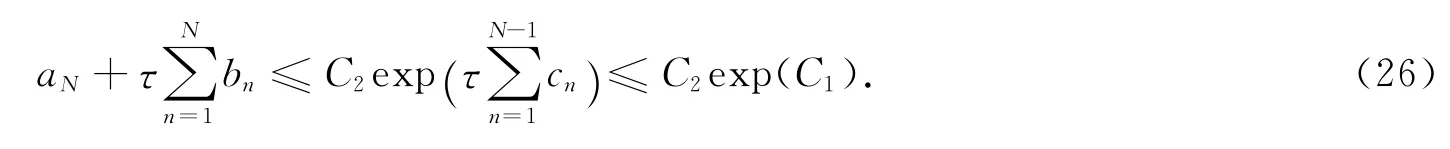
定理3 假设考虑的时间区间为t∈［0，T］，u（t）为连续问题（2），（3）的解，uu为离散数值格式（9）在t＝tn时刻的解，如果满足τ≤1／4，则我们有如下误差估计：

证 首先，计算截断误差

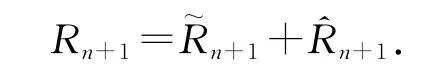
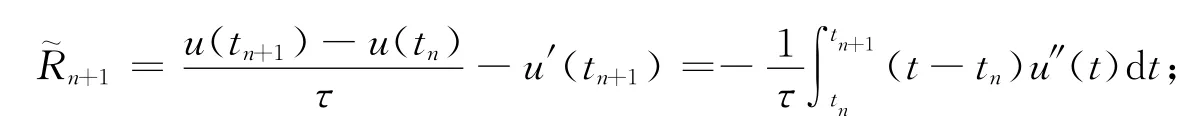
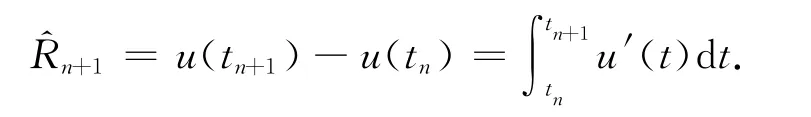
由Cauchy－Schwarz不等式得到

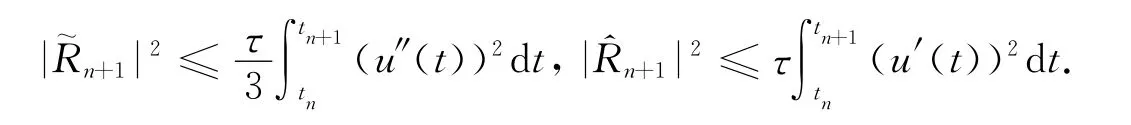
因此截断误差可以有估计

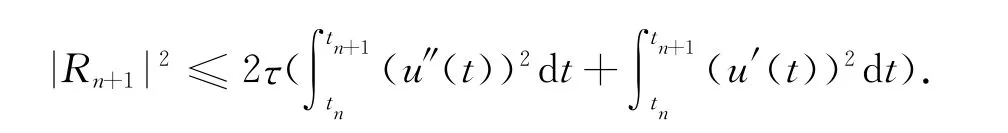
结合方程（2）和数值格式（9），得到误差方程

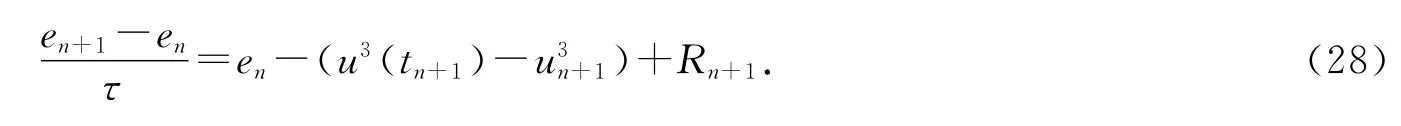
上式两端同乘以2τen＋1，则

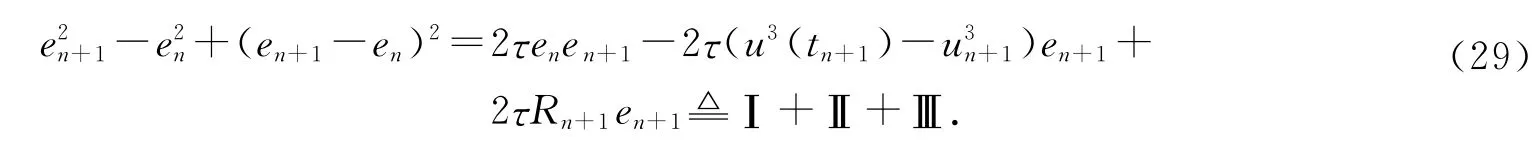
运用Young不等式和引理1，得到如下估计：

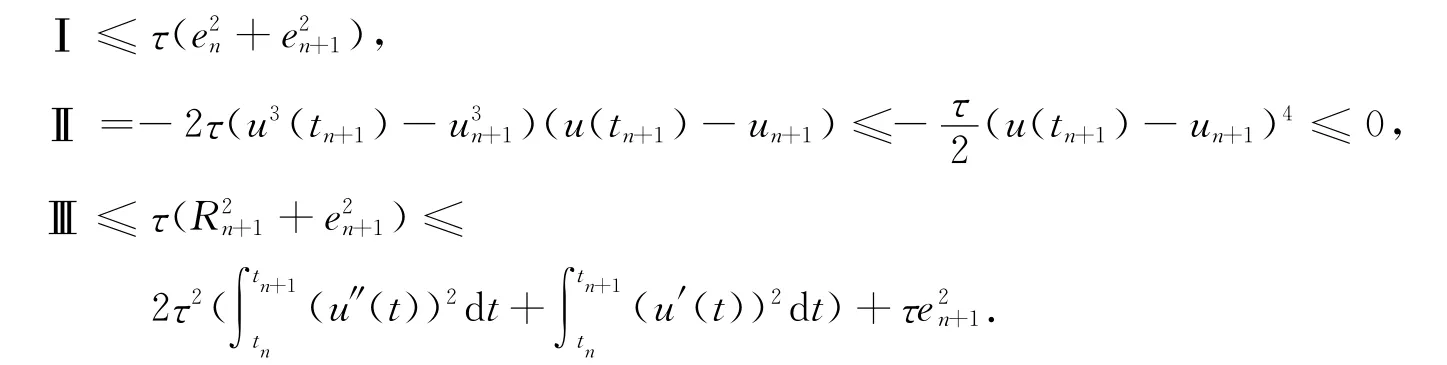
将上述估计代回（29）式，并舍弃一些非必要项，有

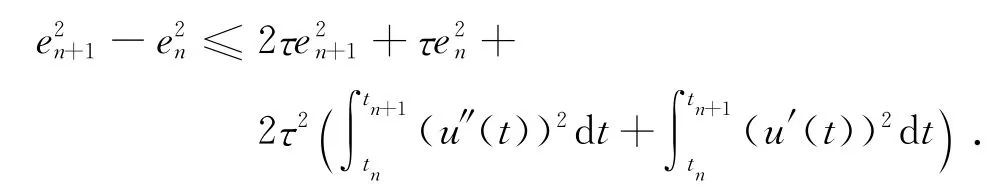
对k＝0，1，…，n（n≤N）进行累加，有

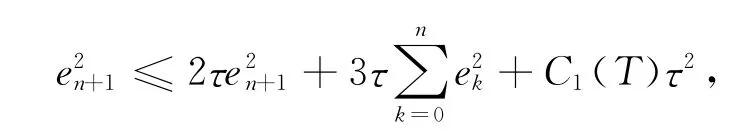
这里

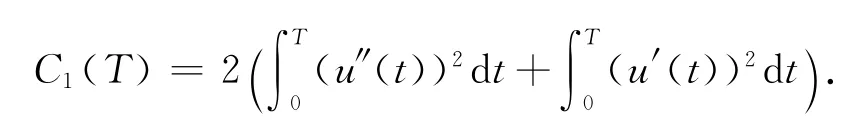
由于τ≤1／4，故应用离散的Gronwall不等式，得到

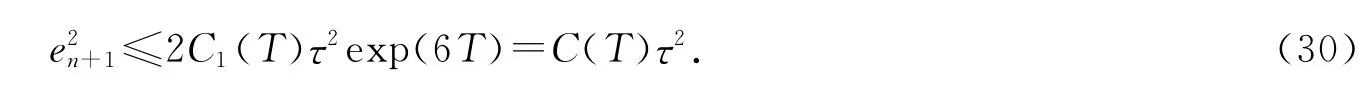
两边开方即得证.

为方便起见，在二阶格式收敛性证明中，我们引入G 范数记号.回忆一下G 范数的定义：设w＝（u，u）T∈R2，定义G 范数

显然矩阵G 是对称正定阵，故上述G 范数可定义.由于

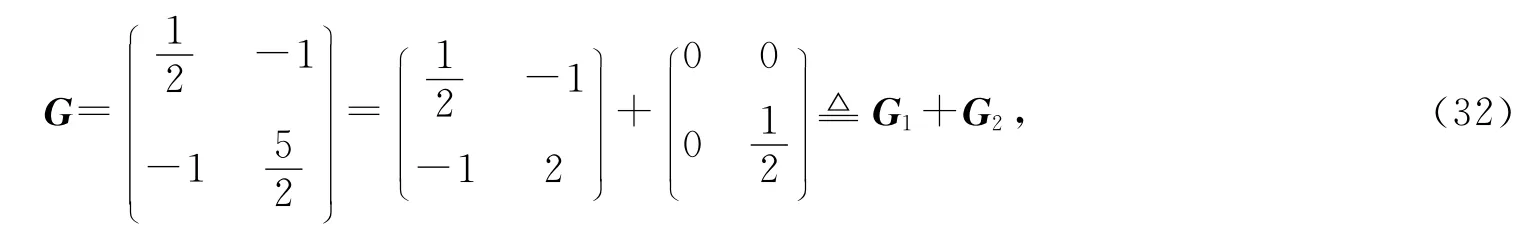
显然G1是半正定矩阵，故有

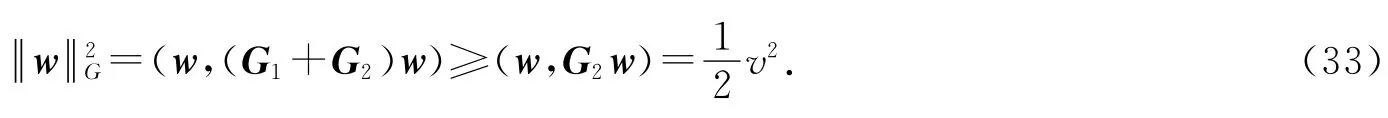
此外，任给vi∈R，i＝0，1，2，有

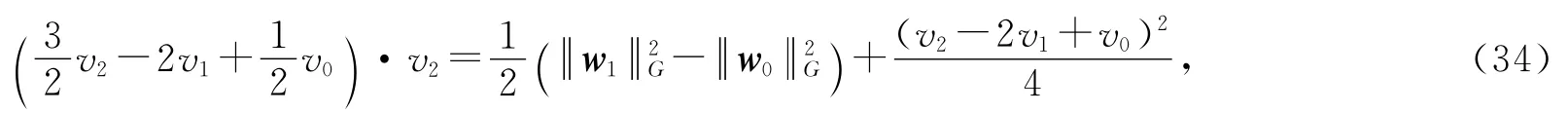
其中w0＝（v0，v1）T，w1＝（v1，v2）T.

定理4 假设考虑的时间区间为t∈［0，T］，u（t）为连续问题（2），（3）的解，un为离散数值格式（10）在t＝tn时刻的解，如果满足τ≤1／16，则我们有如下误差估计：

证 类似于一阶格式.首先，计算截断误差

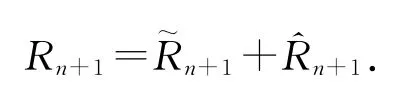
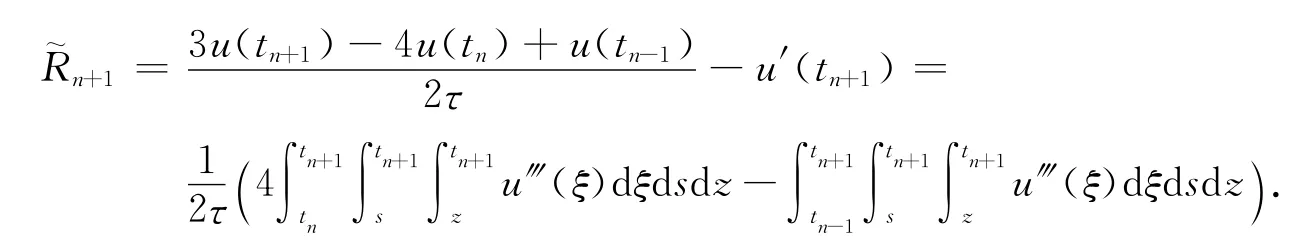
通过简单的估计和Schwarz不等式得到

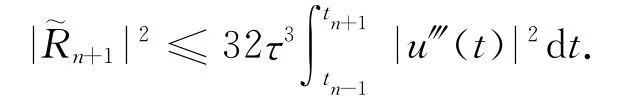
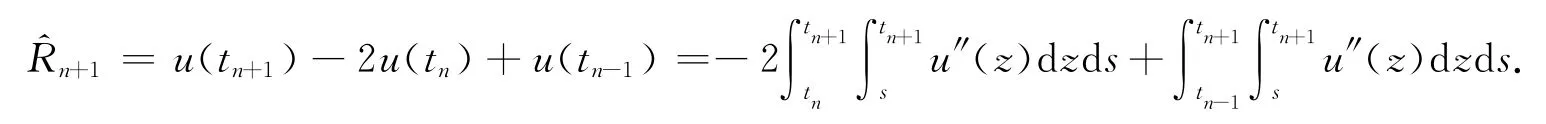
类似地，有

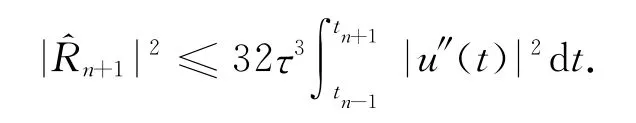
因此截断误差为

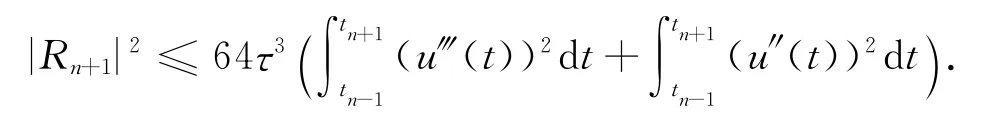
两阶格式（10）的误差方程为

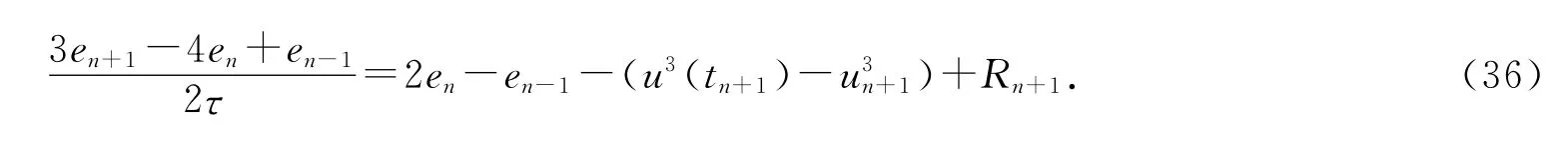
上式两端同乘以2τen＋1，根据Young不等式、引理1和（34）式，有

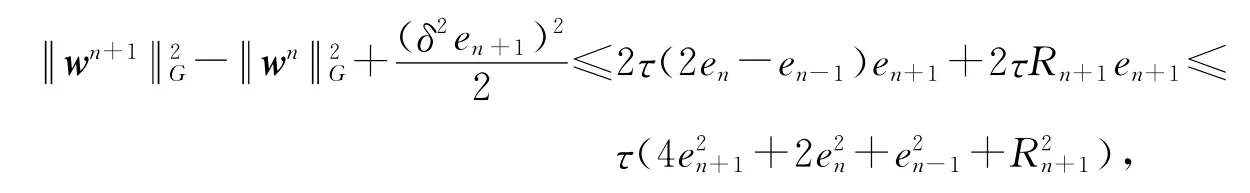
其中wn＋1＝（en，en＋1）T.对k＝0，1，…，n（n≤N）进行累加，舍弃不必要项，并运用不等式（33），有

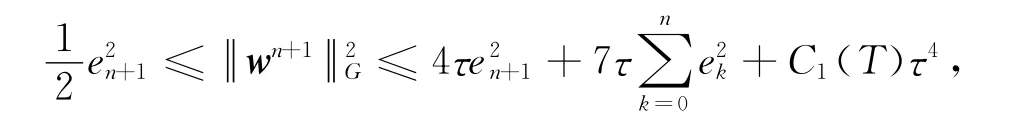
这里

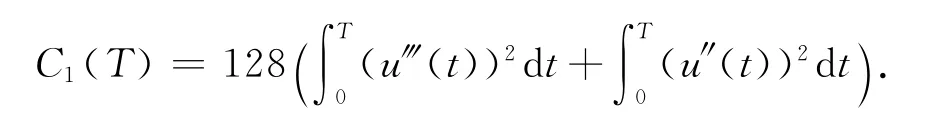
由于τ≤1／16，故应用离散的Gronwall不等式，得到

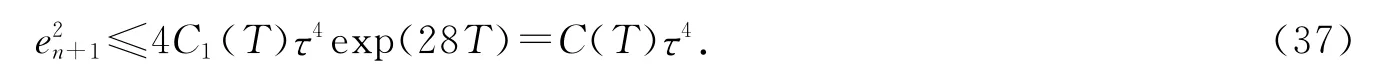
两边开方即得证.

5 数值结果

首先格式（9）和格式（10）都需要求解三次方程

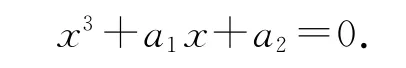
我们已经知道由这两个格式得到的解是唯一的实根，可以利用如下公式来求解：

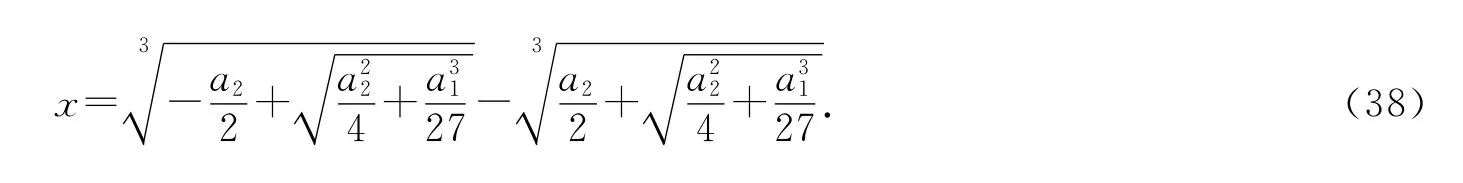
在极端情况下，可能会出现大数相减导致有效位数损失的情况［18］，但由于这里考虑的还是低阶格式，所以舍入误差不在这里讨论.

下面我们先给出初始值的计算结果，从图2（a）可以看到对于不同的初始值（u0＝±0.01，±0.5，±1.5），计算解和精确解结果一致.要提到的是上面的两阶格式的初始值u1是用最简单的显式Euler格式计算得到的，可以证明这样的取法其整体误差还是两阶的.另外我们要说明的是，对于长时间计算T 较大的情况，当τ比较大的时候，在初始状态，解有可能出现“过冲”现象，例如在图2（b）中可以看到，当初始值u0＝0.5，当T＝8，N＝8的时候，对于二阶格式，计算解会大于1，这个现象当增加等分次数时就会消失.这也说明定理3和定理4所要求的条件是充分而非必要的.

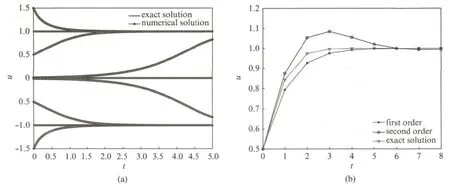
图2 不同初始值的精确解和计算解（a）；T＝8，N＝8时候的数值解（b）Fig.2 （a）Exact and numerical solutions with different initial values；（b）Numerical solutions when T＝8，N＝8

另外以初始值u0＝0.5为例，看看两个计算格式是否分别为一阶和两阶精度.我们计算当T＝1时刻的误差收敛阶，从表1可以看出两格式分别是一阶和两阶收敛的.对于其他的初值可以得到类似的结论.这里要提到的是关于初始值的选取，当步长τ比较小的时候，我们可以用显式Euler格式来得到二阶格式的第二个初始值u1，但是当τ较大或者ε 很小的时候，如果用显式Euler格式会得到定性上错误的解，也就是正的初始值会趋向负的平衡点u＝－1，这是由于u1可能会是个负值.因此我们建议用本文的一阶格式来计算二阶格式u1的值.另外对于长时间计算（大的T），本文的格式都有非常好的结果，与预期一致，解都最终收敛到平衡点.对非常小的ε，这两个格式也是非常稳定的.这里就不再附上数值结果.

表1 粗－细网格误差的收敛阶，等分数从26 到213Tab.1 Convergence order of errors on coarse and fine grids，with Nfrom 26 to 213

6 对Allen－Cahn方程的离散

下面考虑用我们上面构造的例子来求解Allen－Cahn方程：

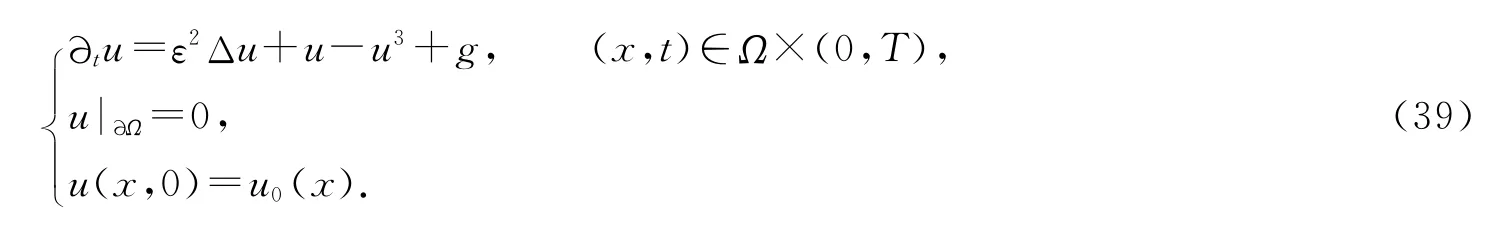
这里时间方向上采用之前所构造的一阶和二阶格式，空间方向上采用经典的五点差分格式来求解方程：

1）一阶格式

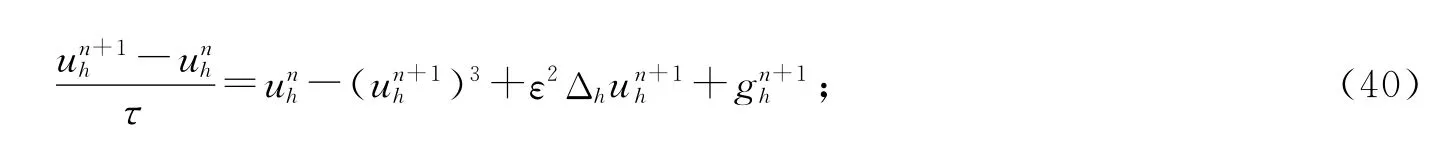
2）二阶格式

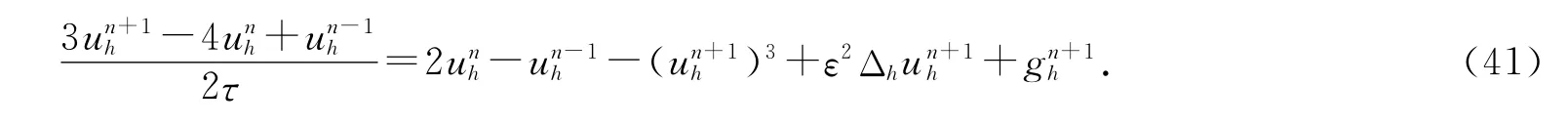
取Ω＝［0，1］×［0，1］，T＝1，ε2＝0.1，方程真解为u（x，t）＝e－tsin（πx1）sin（πx2），g 由u 计算得到.非线性方程采用牛顿法求解，初始迭代值取前两步外推值，即，大多数情况下，这种取法会比初始迭代值取前一步值少迭代一次，从而缩短计算时间.停机准则为＜10－9.首先，验证误差在时间方向上的收敛阶.取τ＝h，τ为时间步长，h为空间步长，err1，err2分别为一阶和二阶格式的误差项.计算结果见表2.然后，验证误差在空间方向上的收敛阶.我们熟知五点差分格式在空间上是二阶收敛的，因此在一阶格式中取τ＝h2，使得时间方向误差和空间方向误差同阶，err 为误差项.计算结果见表3.从表2，表3中可以看出，我们所构造的格式在时间和空间方向上都得到了满意的收敛结果.

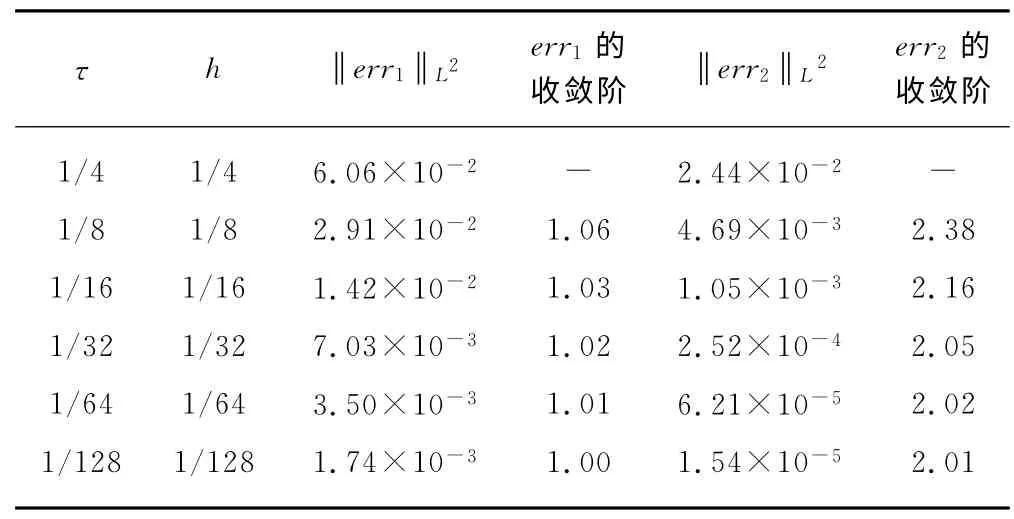
表2 Allen－Cahn方程时间方向的收敛阶分析Tab.2 Convergence analysis in time for Allen－Cahn equations

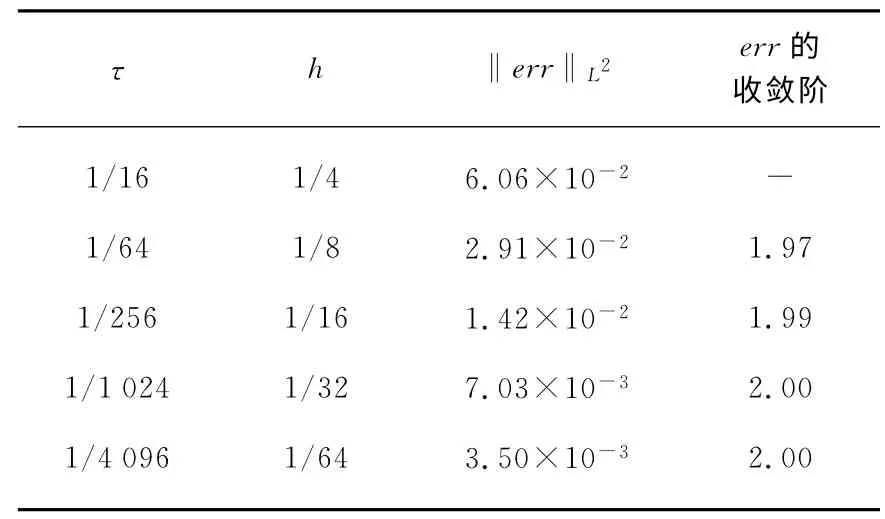
表3 Allen－Cahn方程空间方向的收敛阶分析Tab.3 Convergence analysis in space for Allen－Cahn equations

［1］Hairer E，Wanner G.Solving ordinary differential equations Ⅰ：Nonstiff and problems［M］.Berlin：Springer－Verlag，1993.

［2］Hairer E，Wanner G.Solving ordinary differential equations Ⅱ：Stiff and differential－algebraic problems［M］.Berlin：Springer－Verlag，1996.

［3］Li B，Liu J G.Thin film epitaxal with or without slope selection［J］.Euro J Appl Math，2003，14（6）：713－743.

［4］Li B，Liu J G.Epitaxial growth without slope selection：Energetics，coarsening and dynamic scaling［J］.J Nonlinear Sci，2004，14（5）：429－451.

［5］Xu C J，Tang T.Stability analysis of large time－stepping methods for epitaxial growth models［J］.SIAM J Numer Anal，2006，44（4）：1759－1779.

［6］夏 茜，陈文斌，刘建国.关于薄膜外延生长模型隐式全离散格式的误差分析［J］.高校计算数学学报，2012，34（1）：30－51.

［7］Wang C，Wang X M，Wise S M.Unconditionally stable schemes for equations of thin film epitaxy［J］.Discrete Contin Dyn Syst，2010，28（1）：405－423.

［8］Chen W B，Wang Y Q.A mixed finite element method for thin film epitaxy［J］.Numer Math，2012，122（4）：771－793.

［9］Qiao Z H，Sun Z Z，Zhang Z R.The stability and convergence of two linearized finite difference schemes for the nonlinear epitaxial growth model［J］.Numer Meth Part Differ Equ，2012，28（6）：1893－1915.

［10］Chen W B，Conde S，Wang C，et al.A linear energy stable scheme for a thin film model without slope selection［J］.J Sci Comput，2012，52（3）：546－562.

［11］Chen W B，Wang C，Wang X M，et al.A linear iteration algorithm for a second order energy stable scheme for a thin film model without slope selection［J］.J Sci Comput，2014，59（3）：574－601.

［12］Eyre D J.Unconditionally gradient stable time marching the Cahn－Hilliard equation［M］∥Computational and Mathematical Models of Microstructhral Evolution，Vol.52.Warrendale：Materials Research Society，1998：1686－1712.

［13］Chen W B，Gunzburger M，Sun D，et al.Efficient and long－time accurate second－order methods for Stokes－Darcy system［J］.SIAM J Numer Anal，2013，51（5）：2563－2584.

［14］Collins C，Shen J，Wise S M.An efficient，energy stable scheme for the Cahn－Hilliard－Brinkman system［J］.Commun Comput Phys，2013，13（4）：929－957.

［15］Baskaran A，Hu Z Z，Lowengrub J S，et al.Energy stable and efficient finite－difference nonlinear multigrid schemes for the modified phase field crystal equation［J］.J Comput Phys，2013，250：270－292.

［16］Wang L D，Chen W B，Wang C.An energy－conserving second order numerical scheme for nonlinear hyperbolic equation with an exponential nonlinear term［J］.J Comput Appl Math，2015，280：347－366.

［17］Layton W.Introduction to the numerical analysis of incompressible viscous flows［M］.Philadelphia：SIAM，2008.

［18］Higham N J.Accuracy and stability of numerical algorithms，Second edition［M］.Philadelphia：SIAM，2002.