附件G：AuCuI（）化合物无序化过程的合金基因浓度跟踪研究

G.1　混合焓实验路径的合金基因浓度跟踪法

对于给定成分的合金，由等有序度Gibbs能平衡路径法获得最小Gibbs能（）-T路径（见图G.1（a）），在平衡等有序度（-T）网络图中绘制（-T ）亚平衡路径（见图G.1（b）），随后相继获得混合Gibbs能（-T ）（见图G.1（c）），有序度（σ-T ）（见图G.1（d））、合金基因浓度（（-T）（见图G.2）和其他性质s,x（qs,x-T）亚平衡全息网络路径图（见图G.3～G.18）[6]：（-T）→（-T）→（σ-T）→（（）-T）→（q-T）s,xs,xs,x

图G.1　AuCuI（）化合物无序化的EHNP和SHNP路径图Fig.G.1　EHNP- and SHNP-charts on disordering AuCuI（）：（a）Minimal mixed Gibbs energy-Tpath obtained by iso-order degree Gibbs energy equilibrium path method；（b）Experimental mixed enthalpy-T path method based on network chart of iso-order degree mixed enthalpies equilibrium paths, attaching equilibrium-T path；（c）（OABC）and（Oabc）paths of equilibrium and subequilibrium order→disorder transitions, wheredenoting superheated driving Gibbs energy；（d）σe（OABCD）and σs（OabcD）paths of equilibrium and subequilibrium order→disorder transitions, where Δσhdenoting hysteresis order degree

（To be continued）

图G.2 AuCuI（）化合物无序化的合金基因浓度跟踪图Fig.G.2 AG-concentration SHNP charts on disordering AuCuI（）：（a）, （b）Three-dimension-T-i and-T-i SHNP charts；（c）, （d）Two-dimension iso-order degree-i and-i SHNP charts；（e）, （f）Two-dimension iso-Gibbs energy level-σ and-σ SHNP charts

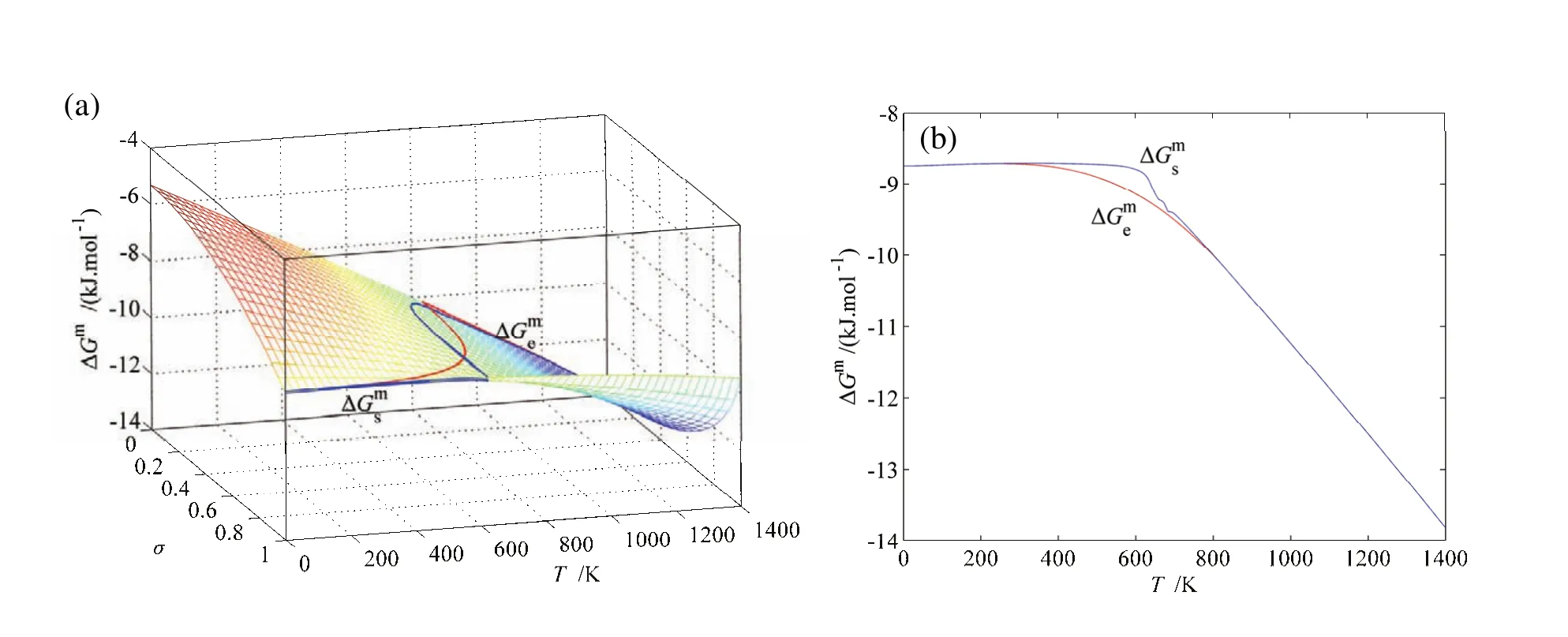
图 G.3 AuCuI（）化合物无序化时载有平衡和亚平衡路径的ΔGm-平衡全息网络路径图Fig.G.3 EHNP charts with EHNP and SHNP curves of the first order thermodynamic properties on disordering AuCuI（）：（a）Three-dimension mixed Gibbs energy ΔGm-T-σ EHNP chart with-T and-T paths；（b）-T and-T　paths

图 G.4 AuCuI（）化合物无序化时载有平衡和亚平衡路径的-平衡全息网络路径图Fig.G.4　EHNP charts with EHNP and SHNP curves of the first order thermodynamic properties on disordering AuCuI（）：（a）Three-dimension mixed characteristic Gibbs energy ΔG∗m-T-σ EHNP chart with-T and-T paths；（b）-T　and-T paths

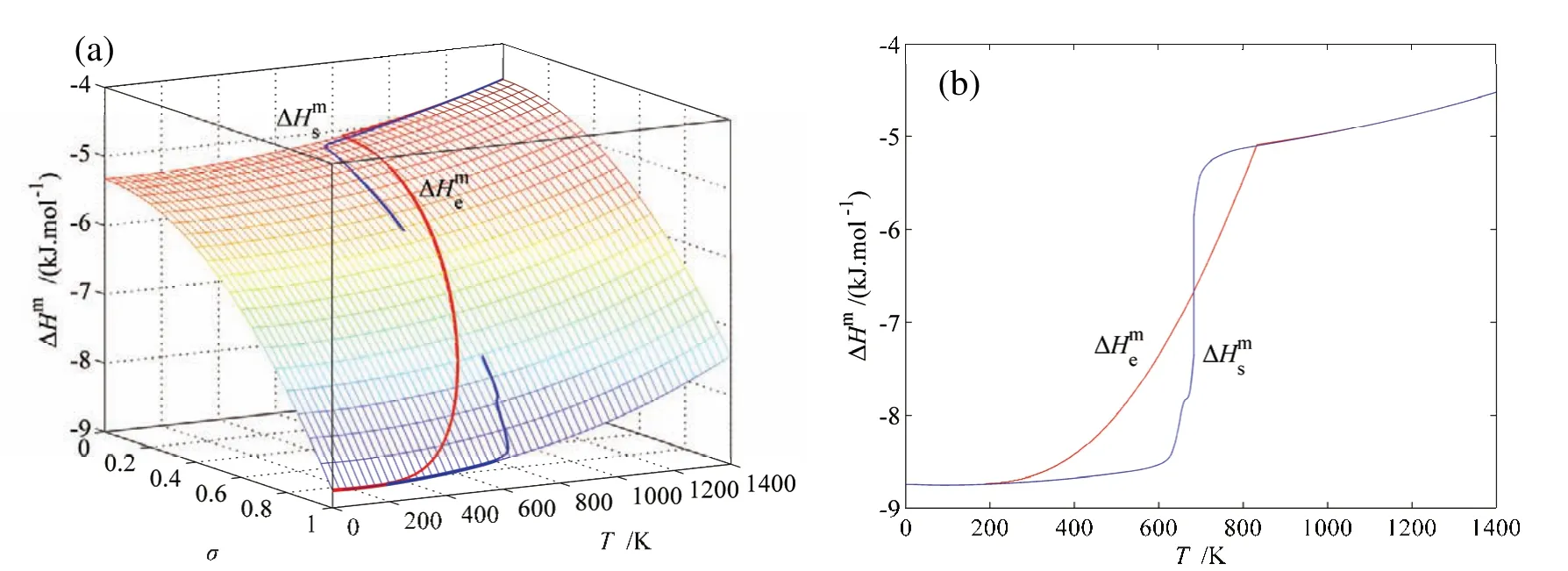
图G.5 AuCuI（）化合物无序化时载有平衡和亚平衡路径的ΔHm-平衡全息网络路径图Fig.G.5　EHNP charts with EHNP and SHNP curves of the first order thermodynamic properties on disordering AuCuI（）：（a）Three-dimension mixed enthalpy ΔHm-T-σ EHNP chart with-T and-T paths；（b）-T and-T　paths

图G.6　AuCuI（）化合物无序化时载有平衡和亚平衡路径的ΔEm-平衡全息网络路径图Fig.G.6　EHNP charts with EHNP and SHNP curves of the first order thermodynamic properties on disordering AuCuI（）：（a）Three-dimension mixed potential energy ΔEm-T-σ EHNP chart with-T and-T paths；（b）-T and-T　paths

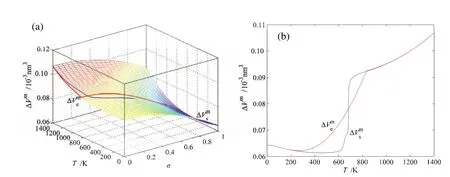
图G.7 AuCuI（）化合物无序化时载有平衡和亚平衡路径的ΔVm-平衡全息网络路径图Fig.G.7　EHNP charts with EHNP and SHNP curves of the first order thermodynamic properties on disordering AuCuI（）：（a）Three-dimension mixed volume ΔVm-T-σ EHNP chart with-T and-T paths；（b）-T and-T　paths

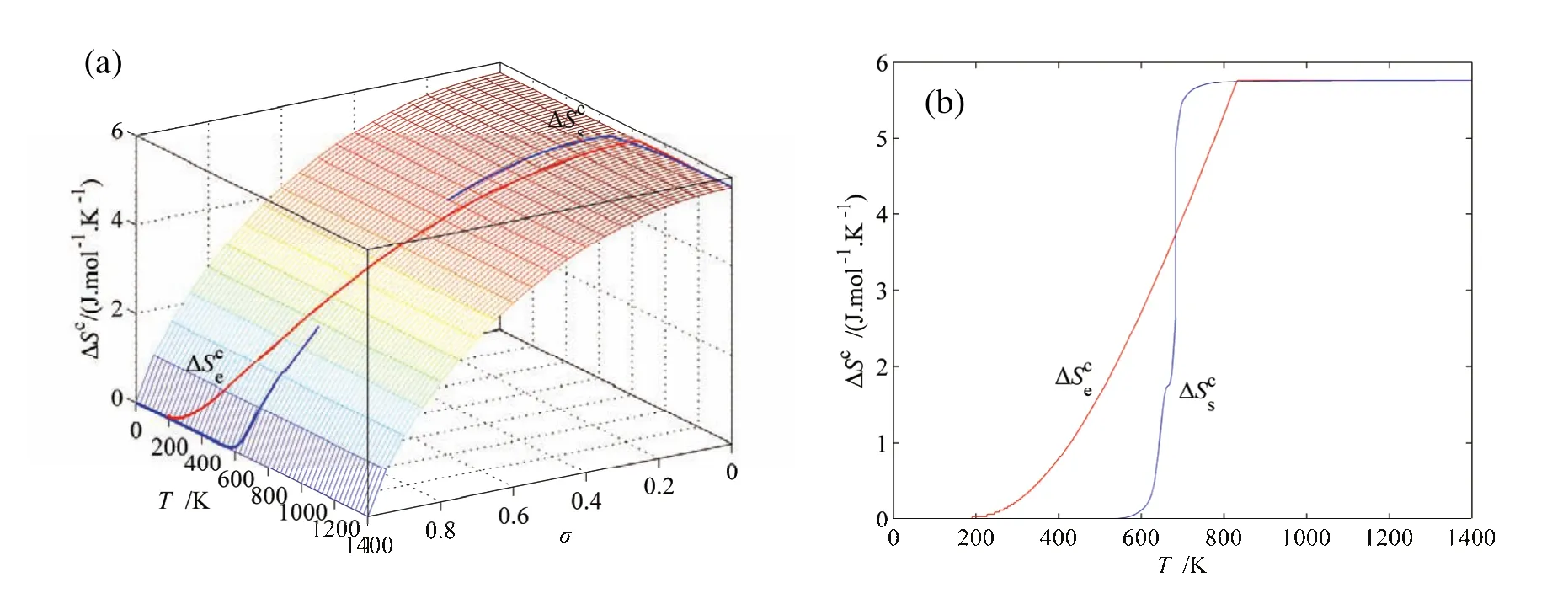
图G.8　AuCuI（）化合物无序化时载有平衡和亚平衡路径的Sc-平衡全息网络路径图Fig.G.8　EHNP charts with EHNP and SHNP curves of the first order thermodynamic properties on disordering AuCuI（）：（a）Three-dimension configurational entropy Sc-T-σ EHNP chart with-T and-T paths；（b）-T and-T paths

图 G.9 AuCuI（）化合物无序化时载有平衡和亚平衡路径的ΔUm.v-平衡全息网络路径图Fig.G.9 EHNP charts with EHNP and SHNP curves of the first order thermodynamic properties on disordering AuCuI（）：（a）Three-dimension generalized vibration energy-T-σ EHNP chart with-T and-T paths；（b）-T　and-T paths

图G.10 AuCuI（）化合物无序化时载有平衡和亚平衡路径的ΔSv-平衡全息网络路径图Fig.G.10　EHNP charts with EHNP and SHNP curves of the first order thermodynamic properties on disordering AuCuI（）：（a）Three-dimension generalized vibration entropy ΔSv-T-σ EHNP chart with-T and-T paths；（b）-T and-T paths

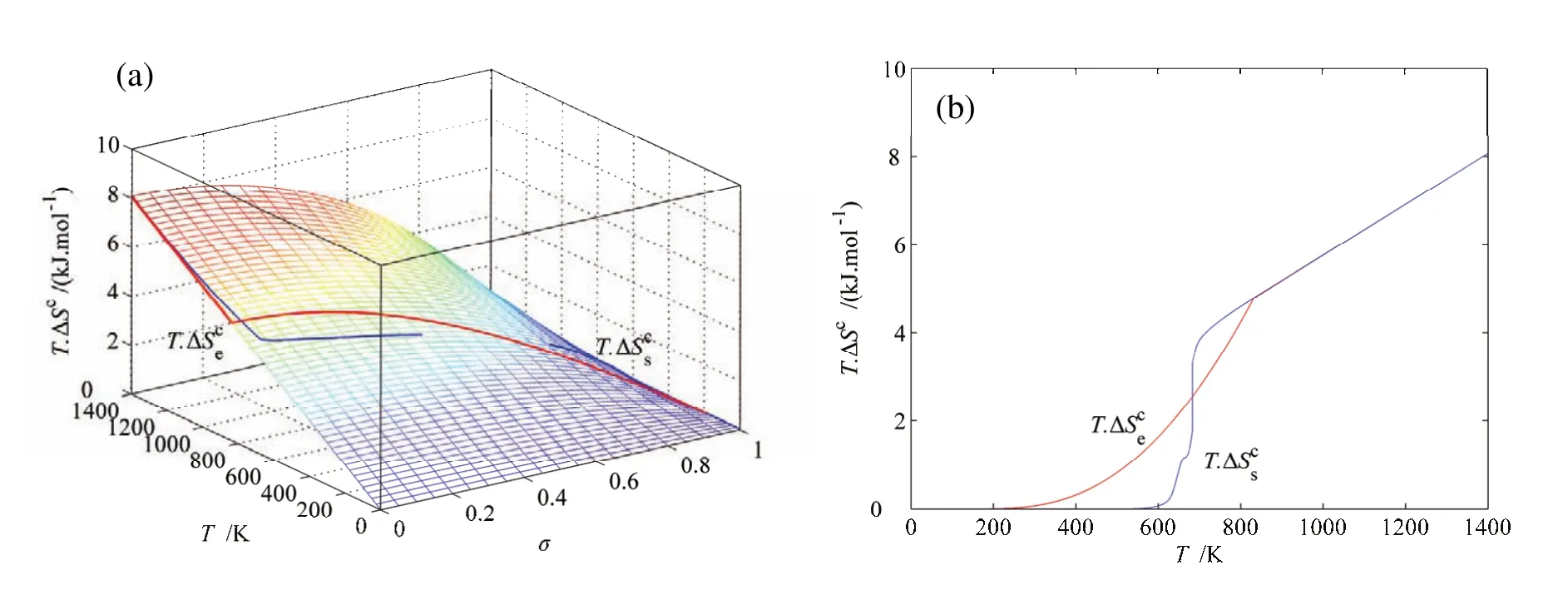
图 G.11 AuCuI（）化合物无序化时载有平衡和亚平衡路径的TSc-平衡全息网络路径图Fig.G.11　EHNP charts with EHNP and SHNP curves of the first order thermodynamic properties on disordering AuCuI（）：（a）Three-dimension configurational entropy energy TSc-T-σ EHNP chart with-T and-T paths；（b）-T and-T paths

图G.12　AuCuI（）化合物无序化时载有平衡和亚平衡路径的TΔSv-平衡全息网络路径图Fig.G.12　EHNP charts with EHNP and SHNP curves of the first order thermodynamic properties on disordering AuCuI（）：（a）Three-dimension generalized vibration entropy energy TΔSv-T-σ EHNP chart with-T and-T paths；（b）-T　and-T paths

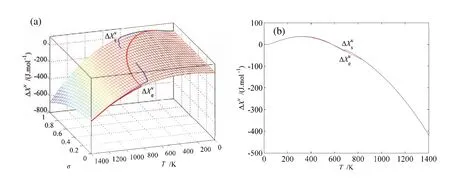
图 G.13　AuCuI（）化合物无序化时载有平衡和亚平衡路径的ΔXv-平衡全息网络路径图Fig.G.13　EHNP charts with EHNP and SHNP curves of the first order thermodynamic properties on disordering AuCuI（）：（a）Three-dimension generalized vibration free energy ΔXv-T-σ EHNP chart with-T and-T paths；（b）-T　and-T paths

图G.14　AuCuI（）化合物无序化时载有平衡和亚平衡路径的c-x-T平衡全息网络路径图pFig.G.14　The second order thermodynamic properties （heat capacity）on disordering AuCuI（）：（a）-T and-T　paths on cp-x-T EHNP diagram；（b）-T and-T paths

图G.15　AuCuI（）化合物无序化时载有平衡和亚平衡路径的c-T-σ平衡全息网络路径图pFig.G.15　The second order thermodynamic properties （heat capacity）on disordering AuCuI（）：（a）-T and-T　paths on c-T-σ EHNP diagram；（b）-σ and-σ pathsp

图 G.16　AuCuI（）化合物无序化时载有平衡和亚平衡路径的热膨胀α-x-T平衡全息网络路径图Fig.G.16　The second order thermodynamic properties （thermal expansion coefficient）on disordering AuCuI（）：（a）αe-T　and αs-T paths on α-x-T EHNP chart；（b）αe-T and αs-T paths

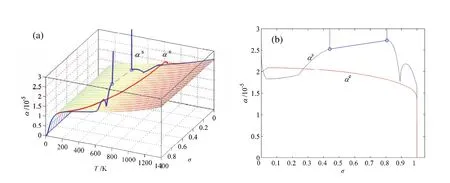
图 G.17 AuCuI（）化合物无序化时载有平衡和亚平衡路径的热膨胀α-T-σ平衡全息网络路径图Fig.G.17　The second order thermodynamic properties （thermal expansion coefficient）on disordering AuCuI（）：（a）αe-T　and αs-T paths on α-T-σ EHNP diagram；（b）αe-σ and αs-σ paths

（To be continued）

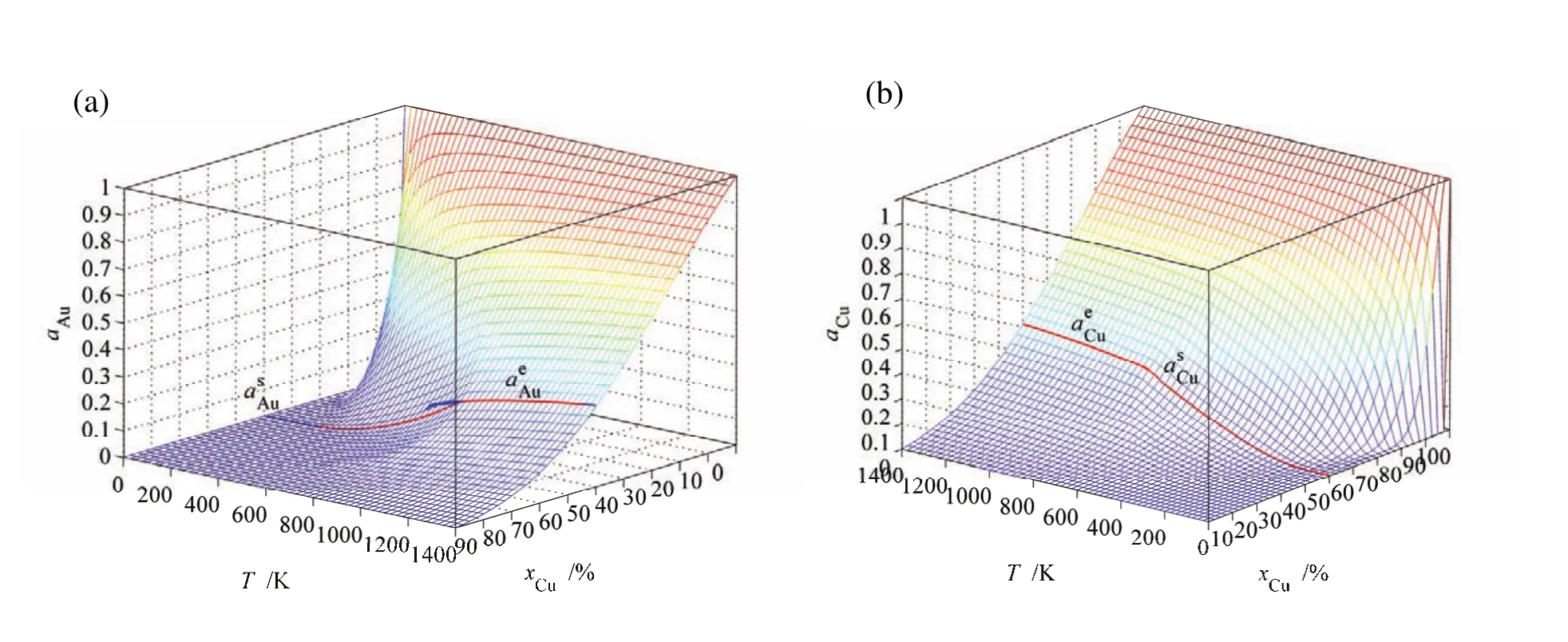
图G.18　AuCuI（）化合物无序化时载有平衡和亚平衡路径的活度a-平衡全息网络路径图Fig.G.18　Activities on disordering AuCuI（）：（a）, （b）-T,-T and-T,-T paths on aAu-x-T and aCu-x-T EHNP diagrams；（c）, （d）-T,-T and-T,-T paths；（e）, （f）-T,-T and-T ,-T paths on a-T-σ and a-T-σ EHNP charts；（g,h）-σ,-σ and-σ,-σAuCupaths

G.2　AuCuI（）无序化路径分析[6]

我们采用实验生成焓路径的合金浓度跟踪法，确定了AuCuI（）化合物的统计非均匀亚平衡和递次性有序一无序转变路径：AuCuI（）→AuCu（H）→PTP-AuCu →SPAP-AuCu（L）→AuCu（D）。该路径的动力学特征与加热速度的关系受RA-SA机制、过热驱动Gibbs能、跳变有序度，以及高温时原子一空位移动机制等控制：

1）当0≤T＜Tonset（593 K）时，它是有序度不变的AuCuI（）亚稳期。

2）当Tonset＜T≤620 K，1.000＞σs≥0.990时，它是高有序度合金AuCu（H）的生长期（见图9（a）和（b））。它具有晶胞尺度的不均匀性：含有较多的3（RA-SA）晶胞的早期一（RA-SA）晶胞区，含有较少的3（RA-SA）晶胞的中期一（RA-SA）晶胞区，没有3（RA-SA）晶胞的晚期一AuCuI（）晶胞区（见图G.19（c））。

3）当620 K＜T≤650 K，0.990＞σs≥0.925时，它是统计周期反向（SPAP）AuCuII区的生长期（见图9（c）和（d））。它具有区域尺度的不均匀性：含有较多的3（RA-SA）晶胞的原早期一（RA-SA）晶胞区成长为早期一（SPAP）-AuCuII区，含有较少的3（RA-SA）晶胞的原中期一（RA-SA）晶胞区成长为含有较多的3（RA-SA）晶胞的中期一（RA-SA）晶胞区，原晚期一AuCuI（）晶胞区成长为含有较少的3（RA-SA）晶胞的晚期一（RA-SA）晶胞区（见图G.19（d））。此时，亚平衡合金具有区域尺度的不均匀性：AuCu（H）区和SPAP-AuCuII区共存，它可称之为“伪二相（PTP）”AuCu合金。

4）当650 K＜T＜683 K，0.925＞σs＞0.807时，它是SPAP-AuCuII合金的成熟期（见图9（e）和（f））。在此阶段，SPAP-AuCuII合金含有早期一，中期一和晚期一（SPAP）-AuCuII区。

5）当0.807≥σs≥0.786时，它是SPAP-AuCuII合金的跳变期（见图9（g）和（h））。在此阶段，跳变合金基因浓度呈现最大“涌现”现象。跳变温度Tj由跳变有序度和过热驱动Gibbs能决定，后者与加热速度有关。

6）当0.4545≥σs＞0时，它是低有序度AuCu（L）合金的存在期（见图9（g）和（h））。当σs=0时，即T≥Tc（683 K），合金AuCu（D）处于无序状态。

图 G.19　AuCuI（）化合物无序化时3（RA-SA）机制和晶胞尺度与区域尺度不均匀性简图Fig.G.19　The 3（RA-SA）mechanism and schemes of cell-scale and region-scale heterogeneities on disordering AuCuI（）：（a）AG arranging structure after A-manner alternating in 3（RA-SA）mechanism of threepairs in a single cell；（b）AG arranging structure after B-manner alternating in 3（RA-SA）mechanism of threepairs in a single cell；（c）AuCu（H）alloy containing three regions with cell-scale heterogeneity；（d）PTP-[AuCuI（H）+PAP-AuCuII] alloy containing three regions with region-scale heterogeneity；（e）AG arranging structure of a early SPAP-AuCuII cell

REFERENCES

[1] CAHN R W, HAASEN P.Physical metallurgy[M].Elsevier Science Amsterdam, 1996：1-46.

[2] OSTP.Materials genome initiative for global competitiveness[R].Washington D C：Office of Science and Technology Policy, 2011.

[3] 谢佑卿.金属材料系统科学[M].长沙 ：中南工业大学出版社, 1998.XIE You-qing.Systematic science of metallic materials[M].Changsha：Central South University of Technology Press, 1998.

[4] XIE You-qing.Systematic Science of Alloys[M].Changsha：Central South University Press, 2012.

[5] XIE You-qing, LI Xiao-bo, LIU Xin-bi, NIE Yao-zhuang, PENG Hong-jian.Alloy gene Gibbs energy partition function and equilibrium holographic network phase diagrams of AuCu-type sublattice system[J].International Journal of Communications, Network and System Sciences, 2013, 12（6）：415-442.

[6] XIE You-qing, PENG Hong-jian, LIU Xin-bi, LI Xiao-bo, NIE Yao-zhuang.New atom movement mechanism for tracking path on disordering AuCuI（）compound[J].Transactions of Nonferrous Metals Society of China, 2014, 24（10）：3221-3256.

[7] XIE You-qing, LI Xiao-bo, LIU Xin-bi, NIE Yao-zhuang, PENG Hong-jian.Alloy gene Gibbs energy partition function and equilibrium holographic network phase diagrams of AuCu3-type sublattice system[J].Transactions of Nonferrous Metals Society of China, 2014, 24（11）：3585-3610.

[8] XIE You-qing, NIE Yao-zhuang, LI Xiao-bo, PENG Hong-jian, LIU Xin-bi.Alloy gene Gibbs energy partition function and equilibrium holographic network phase diagrams of Au3Cu-type sublattice system[J].Transactions of Nonferrous Metals Society of China, 2015, 25（1）：211-240.

[9] XIE You-qing, LIU Xin-bi, LI Xiao-bo, PENG Hong-jian, NIE Yao-zhuang.Holographic alloy positioning design system and holographic network phase diagrams of Au-Cu system[J].Transactions of Nonferrous Metals Society of China, 2015, 25（3）：885-906.

[10] SLATER J C.Electronic structure of alloys[J].Journal of Applied Physics, 1937, 8（6）：385-396.

[11] ELLIS D E, AVERRILL F W.Electronic structure of FeCl4anions in the Hartree-Fock-Slater model[J].J Chem Phys, 1974, 60（8）：2856-2864.

[12] BAERENDS E J, ELLIS D E, ROS P.Self-consistent molecular Hartree-Fock- Slater calculations.I.The computational procedure[J].Chem Phys, 1973, 2（1）：41-51.

[13] KIKUCHI R.A theory of cooperative phenomemena[J].Phys Rev, 1951, 81（6）：988-1003.

[14] KIKUCHI R, de FONTAINE D, MURAKAMI M, NAKAMURA T.Ternary phase diagram calculations—II examples of clustering and ordering systems[J].Acta Metallurgica, 1997, 25（2）：207-219.

[15] ASTA M, de FONTAINE D.First-principles study of phase stability of Ti-Al intermetallic compounds[J].J Mater Res, 1993, 8（10）：2554-2568.

[16] OATES W A, ZHANG F, CHEN S L, CHANG Y A.Improved cluster-site approximation for the entropy of mixing in multicomponent solid solutions[J].Physical Review B, 1999, 59（17）：11221-11225.

[17] OZOLINŠ V, WOLVERTON C, ZUNGER A.Cu-Au, Ag-Au, Cu-Ag and Ni-Au Intermetallics：First-principles study of temperature-composition phase diagrams and structures[J].Physical Review B, 1998, 57（12）：6427-6443.

[18] BRAGG W L, F R S, WILLIAMS E J.The effect of thermal agitation on atomic arrangement in alloys[J].Proceedings of the Royal of Society A, 1934, 145（2）：699-730.

[19] BRAGG W L, F R S, WILLIAMS E J.The effect of thermal agitation on atomic arrangement in alloys II[J].Proceedings of the Royal of Society A, 1935, 51（2）：540-566.

[20] ORIANI R A.Thermodynamics of order alloy.II.The gold-copper system[J].Acta Metall, 1954, 2（3）：608-615.

[21] RHINES F N, BOND W E, RUMMEL R A.Constitution of order alloys of the system Copper-Gold[J].Trans Amer Soc Met, 1955, 47（2）：578-597.

[22] KAUFMAN L, BERNTEIN H.Computer calculation of phase diagrams[M].New York：Academic Press, 1970：225.

[23] SUNDMAN B, FRIES S G, OATES W A.A Thermodynamic assessment of the Au-Cu system[J].CALPHAD, 1998, 22（3）：335-354.

[24] SUNDMAN B, FRIES S G, OATES W A.A calphad assessment of the Au-Cu system using the cluster variatiation method[J].Z Metallkd, 1999, 90（5）：267-273.

[25] HILLERT M.The compound energy formalism[J].Journal of Alloys and Compounds, 2001, 320（1）：161-176.

[26] OATES W A.Configurational entropies of mixing in solid alloys[J].J Equilibria Diffusion, 2007, 28（1）：79-89.

[27] 谢佑卿, 聂耀庄, 李小波, 刘心笔, 彭红建, 李艳芬.FP-SSA框架中Au3Cu型有序合金相的特征原子势能配分函数[J].中国有色金属学报, 2011,21（10）：2489-2501.XIE You-qing, NIE Yao-zhuang, LI Xiao-bo, LIU Xin-bi, PENG Hong-jian, LI Yan-fen.Characteristic atom potential energy partition functionof Au3Cu type ordered alloys in FP-SSA Framework[J].The Chinese Journal of Nonferrous Metals, 2011, 21（10）：2489-2501.

[28] 刘梓葵.关于材料基因组的基本观点及展望[J].科学通报, 2013, 58（35）：3618-3622.LIU Z K.Perspective on materials genome[J].Chin Sci Bull （Chin Ver）, 2013, 58（35）：3618-3622.

[29] KAUFMAN L, ǺGREN J.First and second generation-birth of the materials genome[J].Scripta Materialia, 2014, 70（1）：3-6.

[30] 赵继成.材料基因组计划简介[J].自然杂志, 2014, 36（2）：89-104.ZHAO Ji-cheng.A perspective on materials genome initiative[J].Chinese Journal of Nature, 2014, 36（2）：89-104.

[31] 谢佑卿, 马柳莺.广义Vegard定律和广义余氏定理[J].中南矿冶学院学报, 1985, 16（3）：1-10.XIE You-qing, MA Liu-ying.Generalized Vegard’s law and generalized Yu’s law[J].Journal Central-South Institute of Mining and Metallurgy, 1985, 16（3）：1-10.

[32] XIE You-qing, PENG Kun, LIU Xin-bi.Influences of xTi/xAlatomic states, lattice constants and potential-energy planes of ordered FCC TiAl type alloys[J].Physica B, 2004, 344（1/4）：5-20.

[33] XIE You-qing, LIU Xin-bi, PENG Kun.Atomic state, potential energies, volumes, stability and brittleness of ordered FCC TiAl3type alloys[J].Physica B, 2004, 353（1/2）：15-33.

[34] XIE You-qing, PENG Hong-jian, LIU Xin-bi, PENG Kun.Atomic state, potential energies, volumes, stability and brittleness of ordered FCC Ti3Al type alloys[J].Physica B, 2005, 362（1/4）：1-17.

[35] XIE You-qing, TAO Hui-jin, PENG Hong-jian, LIU Xin-bi, PENG Kun.Atomic state, potential energies, volumes, stability and brittleness of ordered FCC TiAl2type alloys[J].Physica B, 2005, 366（1/4）：17-37.

[36] XIE You-qing, LIU Xin-bi, LI Xiao-bo, PENG Hong-jian, NIE Yao-zhuang.Potential energies of characteristic atoms on basis of experimental heats of formation of AuCu and AuCu3compounds[J].Transactions of Nonferrous Metals Society of China, 2009, 19（5）：1243-1256.

[37] XIE You-qing, LIU Xin-bi, LI Xiao-bo, PENG Hong-jian, NIE Yao-zhuang.Volume sequences of characteristic atoms separated from experimental volumes of AuCu and AuCu3compounds[J].Transactions of Nonferrous Metals Society of China, 2009, 19（6）：1599-1617.

[38] XIE You-qing, NIE Yao-zhuang, LIU Xin-bi, LI Xiao-bo, PENG Hong-jian, LI Yan-fen.Potential energies of characteristic atoms separated from first-principles calculated heats of formation of AuCu and AuCu3compounds[C]//XIE You-qing ed.Systematic Science of Alloys.Changsha：Central South University Press, 2012：405-427.

[39] XIE You-qing, NIE Yao-zhuang, LIU Xin-bi, LI Xiao-bo, PENG Hong-jian, LI Yan-fen.Volumes of characteristic atoms separated from first-principles calculated volumes of L10-AuCu and L12-AuCu3compounds[C]//XIE You-qing.Systematic Science of Alloys.Changsha：Central South University Press, 2012：428-460.

[40] 谢佑卿, 马柳莺.晶体价电子结构的理论晶格参量[J].中南矿冶学院学报, 1985, 16（1）：1-10.XIE You-qing, MA Liu-ying.The theoretical lattice parameter of the valence electron of crystal[J].Journal Central-South Institute of Mining and Metallurgy, 1985, 16（1）：1-10.

[41] XIE You-qing.A new potential function with many-atom interactions in solid[J].Science in China （series E）, 1993, 36（1）：90-99.

[42] XIE You-qing, ZHANG Xiao-dong, ZHAO Li-ying, MA Xiu-ling.Electronic structure and properties of Cu metal[J].Science in China （series E）, 1993, 36（4）：487-496.

[43] XIE You-qing.Electronic structure and properties of pure iron[J].Acta Metal Mater, 1994, 42（11）：3705-3715.

[44] XIE You-qing.Relationship between partial and average atomic volumes of components in Au-Ni alloys[J].Transactions of Nonferrous Metals Society of China, 2011, 21（8）：1801-1807.

[45] XIE You-qing, ZHANG Xiao-dong, CHEN Jia-yan.Electronic structure and properties of pure Cobalt[J].Science in China （Series E）, 1996, 39（4）：394-403.

[46] XIE You-qing, LÜ Man-shan, ZHANG Xiao-dong, ZHAO Li-ying.Electronic structure and properties of Ni metal[J].Science in China （Series A）, 1993, 36（4）：495-503.

[47] XIE You-qing, LIU Xin-bi, PENG Hong-jian, NIE Yao-zhuang, LI Xiao-bo, LI Yan-fen.Characteristic atom arranging crystallogphy of alloy phases for Au-Cu system[J].Science China：Technological sciences, 2011, 54（6）：1560-1567.

[48] XIE You-qing, LI Yan-fen, LIU Xin-bi, LI Xiao-bo, PENG Hong-jian, NIE Yao-zhuang.Characteristic atom occupation patterns of Au3Cu, AuCu3, AuCuI and AuCuII based on experimental data of disordered alloys[J].Transactions of Nonferrous Metals Society of China, 2011, 21（5）：1092-1104.

[49] XIE You-qing, MA Liu-ying, ZHANG Xiao-dong, ZOU Ping, ZHAO Li-ying.Microstructure and properties of Cu-Ni alloys[J].Science in China （Series A）, 1993, 36（5）：612-623.

[50] LUPIS CHP.Chemical thermodynamics of materials[M].Amsterdam：North-Holland, 1983：438-469.

[51] LUPIS CHP, ELLIOTT J F.Prediction of enthalpy and entropy interaction coefficients by the “central atoms” theory[J].Acta Met, 1967, 15（2）：265-276.

[52] 陆学善，梁敬魁.铜金二元系中超结构的形成与点阵间隔的变迁[J].物理学报, 1966, 22（6）：669-696.LU Hsueh-shan, LIANG Ching-kwei.The superlattice formation and lattice spacing changes in copper-gold alloys[J].Acta Physica Sinica, 1966, 22（6）：659-696.

[53] LU Hsueh-shan, LIANG Ching-kwei.The existence of the superlattice CuAu3in the Cu-Au system[J].Kexue Tongbao, 1966, 17（9）：395-396.

[54] LU Hsueh-shan, LIANG Ching-kwei.Experimental evidence of order-disorder transitions as of the second degree [J].Kexue Tongbao, 1966, 17（10）：441-443.

[55] SUTCLIFFE C H, JAUMOT F E Jr.Order-disorder in Au-Cu alloy.I.Short-range order in an alloy containing atomic percent Au[J].Acta Metallurgica, 1953, 1（2）：725-730.

[56] JAUMOT F E Jr, SUTCLIFFE C H.Order-disorder in Au-Cu alloy.II.The nature of the order-disorder transformation and long-range order[J].Acta Metallurgica, 1954, 2（2）：63-74.

[57] SCOTT R E.New Complex phase in the copper-gold system[J].Journal of Applied Physics, 1960, 31（12）：2112-2117.

[58] LANG H, UZAWA H, MOHI T, PFEILER W.L12-long-range order in Cu3Au：kinetics and equilibrium as studied by residual resistivity[J].Intermetallics, 2001, 9（1）：9-24.

[59] KEATING D T, WARREN B E.Long-range order in beta-brass and Cu3Au[J].Journal of Applied Physics, 1954, 22（3）：286-290.

[60] BUTLER B D, COHEN J B.The structure of Cu3Au above the critical temperature[J].J Applied Physics, 1989, 65（6）：2214-2219.

[61] 刘大椿.科学活动论[M].北京：人民出版社, 1985：198-204.LIU Da-chun.Theory of scientific activities[M].Beijing：People Press, 1985：198-204.

[62] DUNHAM I, SHIMIZU N, ROE B A, CHISSOE S, HUNT A R, COLLINS J E, BRUSKIEWICH R, BEARE D M, CLAMP M, SMINK L J, AINSCOUGH R, ALMEIDA J P, BABBAGE A, BAGGULEY C, BAILEY J, BARLOW K, BATES K N, BEASLEY O, BIRD C P, BLAKEY S, BRIDGEMAN A M, BUCK D, BURGESS J, BURRILL W D, O'BRIEN K P.The DNA sequence of human chromosome 22[J].Nature, 1999, 402（6761）：489-495.

[63] Francis S.Collins, Ari Patrinos, Elke Jordan, Aravinda Chakravarti, Raymond Gesteland, Le Roy Walters.New Goals for the U.S.Human genome Project：1988～2003[J].Science, 1998, 10（282）：682-689.

[64] Genome Sequence Database：http：//www.ncbi.nim.gov/genome/seq/.

[65] CAO W, CHANG Y A, ZHU J, CHEN S, OATES W A.Thermodynamic modeling of the Cu-Ag-Au system using the cluster/site approximation[J].Intermetallics, 2007, 15（8）：1438-1446.

[66] WEI S–H, MBAYE A A, FERRIRA L G, ALEX Zunger.First-principles calculations of the phase diagrams of noble metals：Cu-Au, Cu-Ag and Ag-Au[J].Phys Rev B, 1987, 36（20）：4163-4185.

（编辑何学锋）