航空发动机主轴承热分析边界条件处理方法

苏 壮，李国权

（中航工业沈阳发动机设计研究所航空发动机动力传输航空科技重点实验室，沈阳110015）

0 引言

滑油系统是航空发动机的重要组成部分[1]，而热分析是航空发动机滑油系统设计的基础[2]。通过滑油系统热分析计算，可以初步确定发动机滑油系统在整个飞行包线内滑油的温度水平、主轴承的工作温度及轴承腔温度场，并最终确定系统循环量、系统冷却方案及轴承腔的冷却隔热措施[3]。对航空发动机主轴承的热分析是滑油系统热分析中的重要环节，轴承腔内由轴承旋转产生的摩擦热以及密封装置的摩擦热是主要的生热热源[4]，航空发动机主轴承是滑油系统进行冷却和润滑的关键部件，由于主轴承自身的发热量较高，其换热边界条件的准确确定和加载决定了主轴承热分析的精度。准确计算主轴承的工作温度对提高滑油系统热分析精度具有重要的理论意义和工程价值。

本文对航空发动机主轴承的边界条件进行了分类及研究。

1 航空发动机主轴承热分析概述

航空发动机主轴承热分析主要包括以下几个方面：

（1）轴承内部生热的计算。轴承内部的生热主要由摩擦热引起，需要计算由摩擦力矩引起的摩擦热的大小。

（2）轴承内部生热在各元件间的分配。根据摩擦热产生的方式，对摩擦热的分配进行如下假设：由载荷引起的摩擦热都在接触区处产生；除载荷外其它因素产生的摩擦热都在滚动体表面处产生(不包括接触区)。

（3）轴承元件表面及与相邻零件接触面间的换热计算。通过分析轴承元件周围的换热状态，确定采用何种换热准则及经验公式，然后再将其加载到所建立的轴承模型中。

（4）建立包括所有未知温度元件(节点)或零件的热平衡方程组，对方程组求解，确定元件或节点的温度值。目前大多借助商业软件来建模和离散化，生成各节点间的方程组，并求解计算，最终得到节点温度及温度分布云图。

2 主轴承热边界条件分析

本文对在试验器上进行试验的主推力球轴进行分析，试验测量数据可以对本文的计算方法进行验证。试验器主要组成部分如图1所示，被试轴承内圈装在简支的主轴上；外圈安装在主体部件座套上，径向和轴向负荷通过液压活塞作用在该座套上，测量轴承外圈温度的热电偶也通过该座套引出。在试验器运转过程中通过自身发热实现对滑油加温，通过调节散热器供水阀实施温度控制。试验器的环境温度为20℃，试验器的轴承供油温度为70℃，在试验过程中记录轴承的转速、载荷和外圈温度。

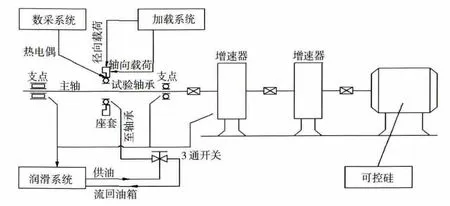
图1 轴承试验器原理

轴承是1个高速的回转体，轴承的温度场沿周向均匀分布，即轴承温度轴对称分布，因此可将3维问题简化为2维问题[5-6]。

建立主轴承的几何模型，根据轴承的工作状态分析轴承各元件周围的边界条件，轴承外部的热边界条件分布如图2所示。其中ha为气侧边界，温度为20℃；ho为油侧边界，温度为70℃；q=0，为绝热边界。气侧和油侧边界皆为对流换热，认为零件接触面间贴合良好，可忽略接触热阻。

轴承的内热源为轴承的摩擦生热，由轴承的摩擦力矩产生。目前国内关于外轴承发热量计算的很多方法经过了试验验证。西北工业大学的刘志全等[7]研究了航空发动机高速滚动轴承热分析中所涉及的几个方面：滚动轴承功率损失的计算模型及几种国内外采用的计算轴承功率损失的公式；滚动轴承的传热计算模型，分析了轴承热计算时所需要的主要换热准则，并对不同的换热准则进行了比较。

浙江大学的蒋兴奇等[8]用热网络法对高速精密角接触球轴承进行了稳态的热分析，分析了轴承内部生热及热量在轴承内外圈的分配，计算了轴承稳态1维温度分布，得到了轴承内部生热与摩擦力矩、载荷、转子自旋有关的结论；还对主轴承的赫兹接触、主轴承的运动和摩擦力矩、主轴承的摩擦热和热阻特性、主轴承的运转特性和温度分布等进行了深入研究。美国的TedricA.Harris[9]研究了滚动轴承的摩擦生热和热传导状况，并对轴承热分析的热网络法进行了研究。

蒋兴奇对轴承摩擦热的分析较为全面，本文采用文献[7]中的公式计算轴承的摩擦热

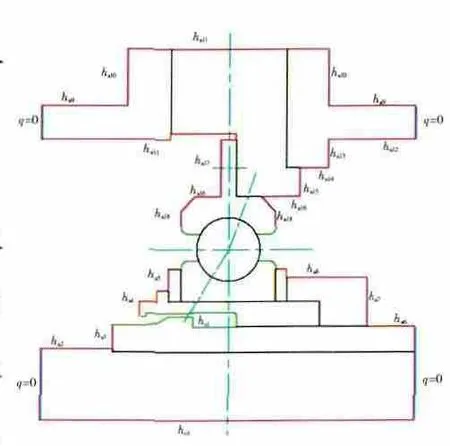
图2 轴承外部热分析边界

式中：Qc为轴承总摩擦热；Mf为总摩擦力矩；ω 为角速度。

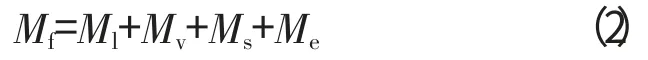
式中：Ml为由载荷引起的力矩；Mv为黏性摩擦力矩；Ms为轴承自转摩擦力矩；Me为滚珠与保持架间的摩擦力矩。

根据Burton和Steph[10]建议，滚动轴承的接触摩擦生热一半进入球，另一半进入套圈。由于轴承接触区的摩擦生热主要由载荷引起，把由载荷引起的Ml所产生的热量加载到滚珠和内外圈的接触区上，并平均分配到接触区上。把由Mv、Ms、Me所产生的热量加到钢球表面上。

4 轴承边界条件分类及处理

轴承内部的边界条件大部分都是对流换热，也就是第3类边界条件，但摩擦热需要单独考虑。考虑到后续有限元模型的加载的可操作性，摩擦热可以通过2种方式来实现。

1种是将摩擦热处理成体积生热率，即导热微分方程中的Φ˙v为单位体积的发热功率[11]

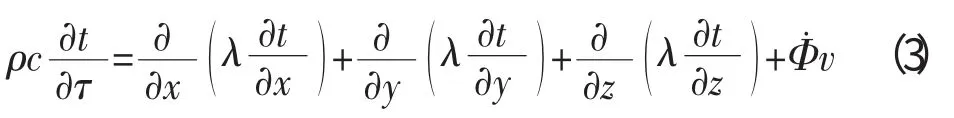
另1种是将摩擦热以热流密度的方式加载到模型表面，也就是加载第3类边界条件的同时，再加载1个第2类边界条件，这时模型边界处为

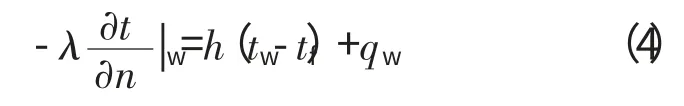
国内外许多学者对轴承内部的对流换热进行了研究。美国TedricA.Harris[9]应用提出的计算公式为

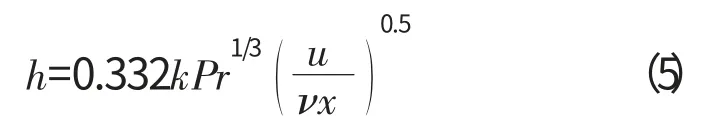
式中：x 为特征长度，可以为节圆直径或沟道直径；u为冷却表面和润滑油之间的相对运动速度，对于球表面与润滑油之间的强迫对流换热，u 取保持架的表面速度，对于内外圈沟道表面与润滑油之间的强迫对流，u 取保持架表面速度的1/3；ν 为润滑油的运动黏度。Harris的这种处理方法是1种比较粗糙的近似方法，以流体层流假设为前提。

西北工业大学的李健等[12]采用式（6）、（7）对轴承处的对流换热进行计算。该方法与Harris的方法的不同之处为其对于层流与湍流进行了区分。式中针对不同的换热面采用不同的尺寸L、雷诺数Re 和普朗特数Pr。

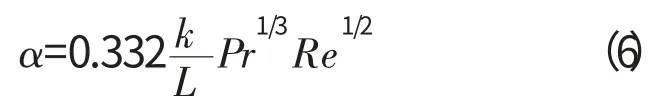
层流时，Re<5×105。

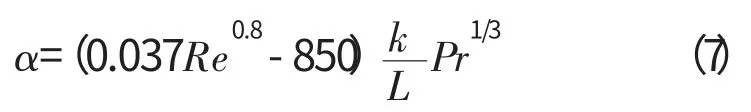
湍流时5×105≤Re<107。

文献[13]给出了目前采用较多的航空发动机主轴承内部的对流换热计算方法

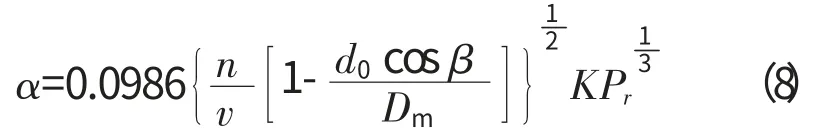
式中：d0为滚动体直径；β 为接触角；n 为转速；Dm为轴承节圆直径。

对比式（5）～（8），由于式（8）中的结构参数完全针对轴承，更适合发动机主轴承的计算，所以选用式（8）计算轴承内部的对流换热系数。

5 主轴承热边界条件的加载方式

在ANSYS热分析中，提供了6种热载荷（温度、热流率、对流、热流密度、生热率和热辐射率），可以施加在实体模型或单元模型上，对于单独的对流换热边界可以直接加载到模型上。对于既有对流换热又有摩擦热的边界处理起来就比较复杂，而轴承中滚动体与内外圈接触区处既有强迫对流换热又有摩擦热。为此，本文分别采用2种方式对滚动体与内外圈接触区的边界进行加载并计算。

5.1 摩擦热按体积生热率的方式加载

将轴承总摩擦热Qc按照式（3）中的Φ˙v 来处理，根据赫兹接触计算，考虑体积生热率的加载方式，将轴承内部模型按接触区的大小进行细化，如图3所示。在4个区域q1、q2、q3、q4上分别加载轴承总摩擦热Qc中1/4的Ml所产生的热量，在q5所示区域加载轴承总摩擦热Qc中由Mv、Ms、Me所产生的热量。计算出上述摩擦热后，分别除以相应区域的体积，得到其体积生热率的结果（见表1），最后将对流换热边界正常加载到模型外表面。

根据文献[14]采用的赫兹计算结果对轴承进行轴对称建模，划分网格后的有限元模型如图4所示。

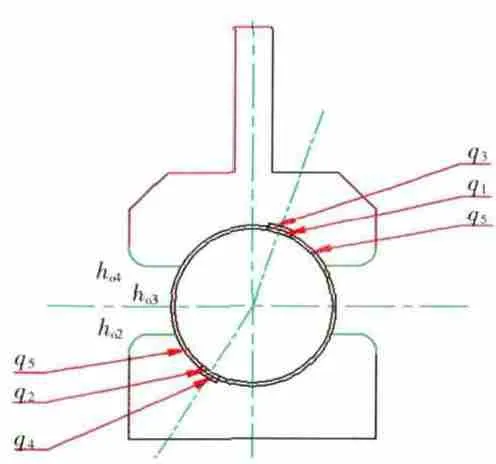
图3 按生热率加载时轴承内部边界

表1 各发热区域的体积生热GW/m3

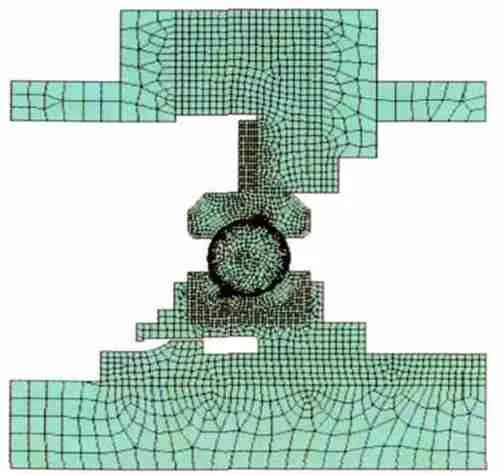
图4 轴承有限元模型

5.2 摩擦热按热流密度的方式加载

根据式（4），将摩擦热中热流密度qw与对流换热同时加载。热流密度是1种面载荷，表示通过单位面积的热流率，又称为热通量（HeatFlux），W/m2。通过单位面积的热流率已知时，可在模型相应的外表面施加热流密度。若输入值为正，表示热流流入单元；反之，则表示热流流出单元。它可以施加在有限元模型的节点及单元上，也可以施加在实体模型的线段和面上。热流密度与对流可以施加在同一外表面，但ANSYS将读取最后施加的面载荷进行计算[15]。为此，需要使用ANSYS中的表面效应单元SURF151来施加2种以上的边界条件。即在表面效应单元SURF151上施加热流密度，而实体上相同位置的对流换热载荷则直接施加在实体单元上，这就实现了在模型的相同位置同时施加2种载荷。

针对热流密度载荷的施加，将轴承内部的边界条件进行了细分，如图5所示。将热流密度Hf1、Hf2施加到滚动体与外圈接触区上，Hf3、Hf4施加到滚动体与内圈接触区上，为1/4的Ml所产生的热量除以相应接触区的面积；将热流密度Hf5施加到滚动体上除去接触区的面积上，由Mv、Ms、Me所产生的热量除以相应滚动体外表面的面积得到。其热流密度的结果见表2，把其余对流换热边界正常加载到模型外表面上。

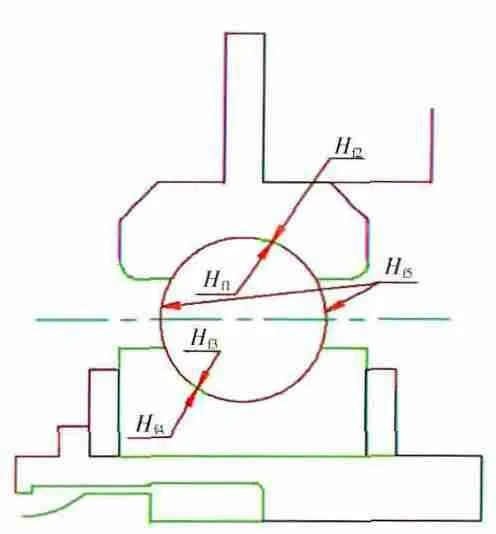
图5 按热流密度加载时轴承内部边界

表2 加载到各表面效应单元上的热流密度105W/m3

2种计算方法的轴承所承受的对流换热边界相同，均按式（8）进行计算，其余边界采用传热学的相应换热准则计算得到对流换热边界条件结果，见表3。

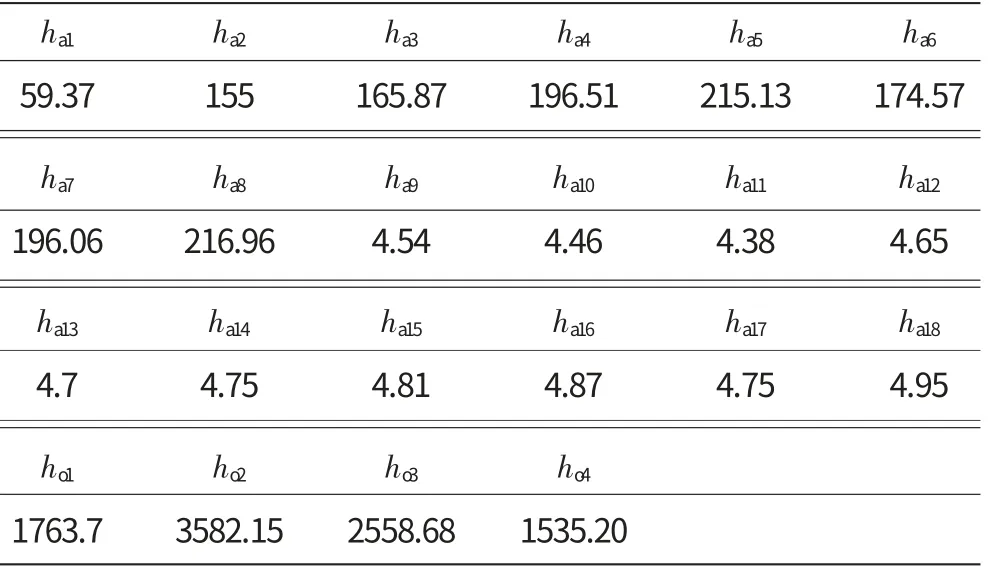
表3 热分析边界条件结果 W/（m2·K）

6 计算结果分析

6.1 摩擦热按体积生热率的方式加载

应用ANSYS将对流换热和体积生热率施加到模型上后进行计算，得到轴承在稳态下的温度分布，如图6所示。为了更好地观察轴承内外圈处的温度分布，显示滚动体隐藏后的结果，如图7所示。在轴承的模型上选取了相同位置的对比点，与试验测量的测试点温度进行对比，对比点如图8所示。

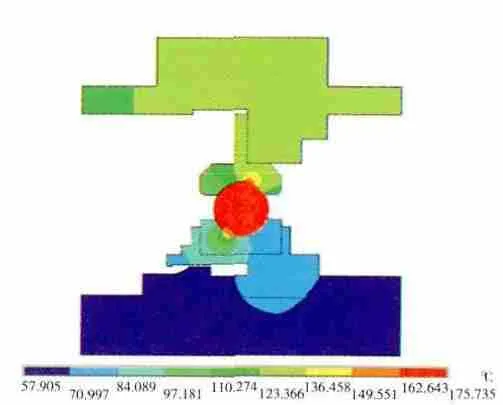
图6 按生热率加载时轴承温度

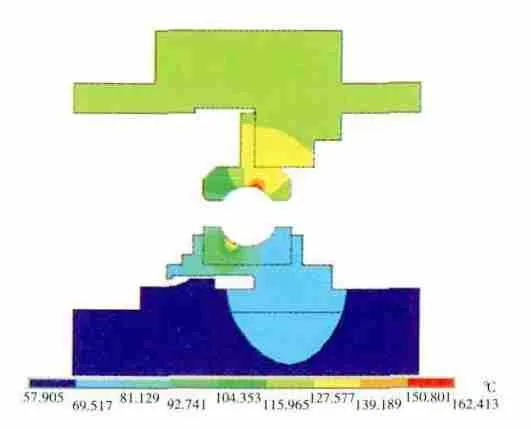
图7 按生热率加载时轴承温度（隐藏滚动体）

计算得到与实际试验测量对比点1的温度分别为121.9、123℃。计算得到与实际试验测量对比点2的温度分别为119.2、120℃。计算结果与试验结果比较接近，证明该加载方式可行。

同样选取如图8所示的对比点进行对比，计算得到的对比点1、2的温度分别为122.2、114.9℃。可见计算结果与试验结果也比较接近，再次证明该加载方式的可行性。

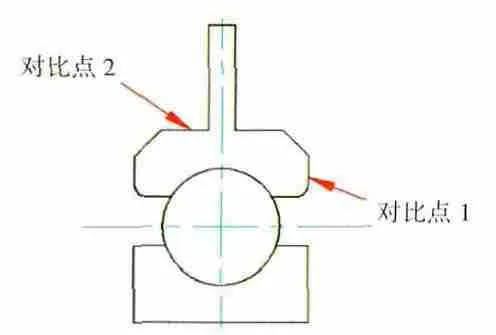
图8 试验器状态轴承模型对比点

6.2 摩擦热按热流密度的方式加载

将热流密度和对流换热共同加载到模型上后，计算得到轴承的稳态温度分布如图9所示，滚动体隐藏后的结果如图10所示。

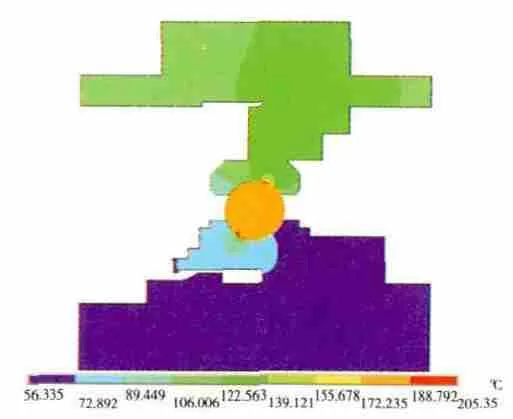
图9 按热流密度加载时轴承温度

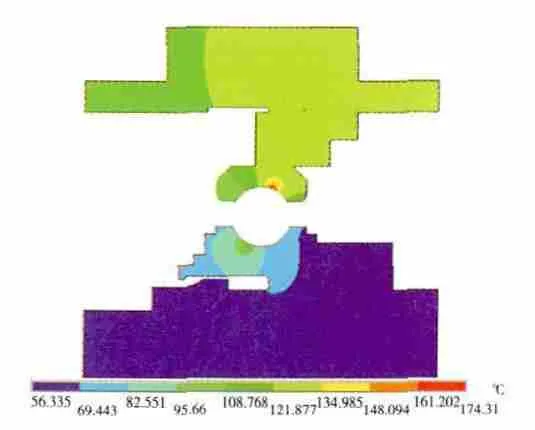
图10 按热流密度加载时轴承温度（隐藏滚动体）

从2种加载方式计算得到的结果来看，热流密度加载方式得到的轴承滚动体接触区的热点温度比另1种计算方法的高。采用体积生热率加载方式得到的轴承滚动体温度则比较平均，采用热流密度加载方式计算的轴承热点温度分布更理想。但将滚动体隐藏后，可见采用2种方法得到的轴承内外圈的热点温度位置及温度分布都比较接近实际轴承温度的假设。并且，采用2种计算方法得到的结果与试验测点的温度比较接近，可以验证2种边界条件加载方式的正确性。

目前，已将上述2种边界条件的加载方式应用到航空发动机轴承腔热分析及润滑系统热分析中。应用体积生热率加载方式计算的航空发动机轴承腔热分析温度分布结果如图11所示；应用热流密度加载方式计算的航空发动机轴承腔热分析温度分布结果如图12所示。2种边界条件的加载方式都取得了较好的计算结果，丰富了润滑系统热分析的手段。

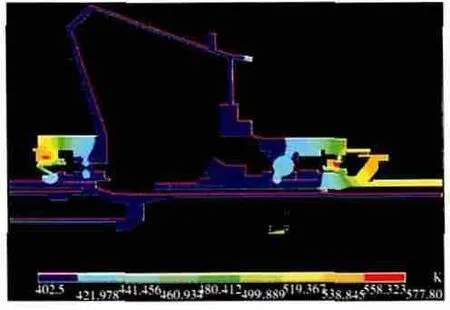
图11 某航空发动机轴承腔热分析温度分布

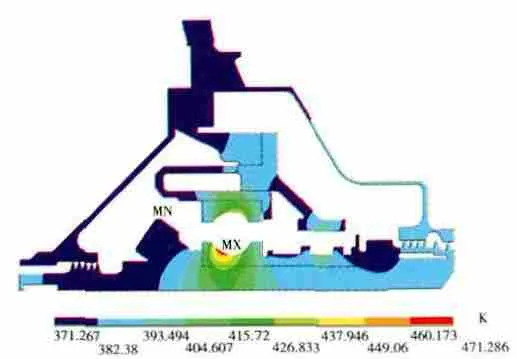
图12 某型航空发动机支点轴承腔温度分布

7 结论

通过对航空发动机主轴承内部边界条件的研究，及2种边界条件加载方式的计算，得到如下主要结论：

（1）在轴承内部边界条件中，可以将第2、3类边界条件复合在一起处理。

（2）可以通过体积生热率将摩擦生热加载到同时具有对流换热的轴承边界上，实现ANSYS热分析中2种不同类型边界条件的加载。

（3）在ANSYS热分析中，可以用表面效应单元实现热流密和对流换热同时加载到轴承内部边界上。

（4）采用表面效应单元的加载方式得到的轴承温度分布更理想，内部热点温度更集中，热点温度比按体积生热率加载的高。

2种边界条件加载方式均经过试验对比，可以将其应用到航空发动机轴承腔及润滑系统热分析中。

[1]李国权.航空发动机滑油系统的现状及未来发展[J].航空发动机，2011，37（6）：49-52.LI Guoquan.Present and future of aeroengine oil system [J].Aeroengine，2011，37（6）：49-52.（in Chinese）

[2]林基恕.航空燃气涡轮发动机机械系统设计[M].北京：航空工业出版社，2005：101-104.LIN Jishu.Aeroengine mechanical system design[M].Beijing：Aeronautical Industry of Publishing Company，2005：101-104.（in Chinese）

[3]《航空发动机设计手册》总编委会.航空发动机设计手册：第12册[M].北京：航空工业出版社，2001：84.Editorial Board of Design Manual of Aeroengine.Design manual of aeroengine（vol.12）[M].Beijing：Aviation Industry Press，2001：84.（in Chinese）

[4]刘友宏，于超.航空发动机滑油系统热分析[J].科学技术与工程，2009，9（22）：6922-6925.LIU Youhong，YU Chao.Research on heat transfer characteristics of lubricating oil system[J].Science Technology and Engineering，2009，39（22）：6922-6925.（in Chinese）

[5]王黎钦，陈观慈，古乐，等.高速圆柱滚子轴承工作温度研究[J].航空动力学报，2008，23（1）：179-183.WANG Liqin，CHEN Guanci，GU Le，et al.Study on operating temperature of high speed cylindrical roller bearings[J].Journal of Aerospace Power，2008，23（1）：179-183.（in Chinese）

[6]葛治美，韩振兴，张恩和，等.航空发动机轴承腔热分析[J].航空动力学报，2005（3）：483-486.GE Zhimei，HAN Zhenxing，ZHANG Enhe，et al.Thermal analysis of aeroengine bearing compartment[J].Journal of Aerospace Power，2005（3）：483-486.（in Chinese）

[7]刘志全，张泳红，苏华.高速滚动轴承热分析[J].润滑与密封，1998（4）：66-68.LIU Zhiquan，ZHANG Yonghong，SU Hua.High speed rolling bearing thermoanalysis[J].Lubrication Engineering，1998（4）：66-68.（in Chinese）

[8]蒋兴奇.主轴轴承热特性及对速度和动力学性能影响的研究[D].杭州：浙江大学，2001.JIANG Xingqi.Study on heat characteristics of spindle bearings and influences on speed and dynamics[D].Hangzhou：Zhejiang University，2001.（in Chinese）

[9]Harris T A.Rolling bearing analysis(5th edition)[M].Boca Raton:CRC Press，2006：207-224.

[10]Burton R A，Staph H E.Thermally activated seizure of angular contact bearing[J].ASLE Trans.，1967（10）：408-417.

[11]赵镇南.传热学[M].北京：高等教育出版社，2002：38-44 ZHAO Zhennan.Heat transfer[M].Beijing：High Education Press，2002：38-44.（in Chinese）

[12]李健，刘志全，袁培益.航空发动机轴承腔温度场计算与测试[J].润滑与密封，1999（1）：58-60.LI Jian，LIU Zhiquan，YUAN Peiyi.Calculation and measurement of temperature fields for an aeroengine bearing oil cavity[J].Lubrication Engineering，1999（1）：58-60.（in Chinese）

[13]Crecelius W J，Pirvics J.Computer program operation manual on SHABERTH：a computer program for the analysis of the steady state and transient thermal performance of shaft bearing systems[R].AD-A 042981.

[14]苏壮，李国权.航空发动机滑油系统断油时主推力球轴承的瞬态热分析[J].航空发动机，2009，35（2）：24-29.SU Zhuang，LI Guoquan.Transient thermal analysis of main thrust ball bearing during fuel cut off for aeroengine oil system [J].Aeroengine，2009，35（2）：24-29.（in Chinese）

[15]张朝晖.ANSYS热分析教程与实例解析[M].北京：中国铁道出版社，2007：124-132.ZHANG Chaohui.ANSYS thermoanalysis tutorial and example[M].Beijing：China Railway Press，2007：124-132.（in Chinese）