基于并行遗传算法的向心涡轮气动优化设计

张金环，周正贵

（南京航空航天大学江苏省航空动力系统重点实验室，南京210016）

0 引言

在微型航空发动机向心涡轮通道中，由于转速较高、离心力和哥氏惯性力影响较大，气流从径向转到轴向，3维特征显著，流道内的二次流和涡系十分复杂，给小尺寸向心涡轮气动设计增加了难度[1]。而向心涡轮的气动性能直接影响到发动机的总体性能，所以在保证向心涡轮流量范围不变的前提下，提高其效率至关重要[2-3]。

随着计算流体力学技术高速发展，3维流动分析与气动设计方法逐渐应用于向心涡轮设计[4-9]。针对向心涡轮已经开展的研究多集中于其初始设计、改进设计、3维流动特性分析，而初始设计、改进设计具有多参数、多约束条件的特点，很多参数的选取需要人员经验，很难得到高效率的涡轮。将数值优化算法与流场计算程序相结合，即可构成向心涡轮的自动优化设计程序，减少对设计人员经验的依赖，并可智能高效地获得高性能叶片。北京航空航天大学马洪波等[10]结合遗传算法和序列2次规划法，以涡轮的气动效率为目标函数，对涡轮叶片进行了气动优化设计；北京理工大学周文哲等[11]对一小尺寸向心涡轮应用商用软件NUMECA的Fine/Design3D模块自动生成样本库，采用改变涡轮轮毂型线及进、出口型线的方法，结合神经网络与遗传算法进行优化，使向心涡轮级在设计工况点 (145000r/min，0.08kg/s)轮周效率提高了1.5%，该优化结果的优劣取决于自由参数及其变化范围的选择，需要一定的人员经验。

本文采用基于并行遗传算法的优化方法，对某微型航空发动机向心涡轮转子叶片进行自动优化设计。数值最优化采用遗传算法，该优化算法具有良好的全局寻优能力，可实现并行优化[12]，并利用多CPU并行大幅度缩短优化耗时。采用商用软件NUMECA进行向心涡轮转子3维流场模拟分析，验证了优化结果。

1 优化方法和过程

向心涡轮叶片气动优化设计由数值最优化、流场数值计算、叶片参数化和目标函数设置模块构成。

1.1 数值最优化原理

向心涡轮考虑的气动性能参数包括流量、膨胀比和轮周效率。其中轮周效率为

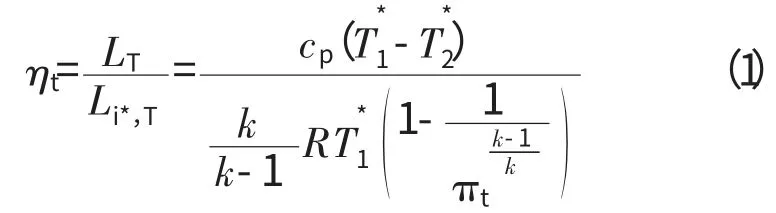
式中：ηt、LT、Li*，T分别为向心涡轮的轮周效率、实际膨胀功和绝热膨胀功分别为向心涡轮的进、出口温度

向心涡轮的膨胀比为

叶片的3维造型决定了向心涡轮叶片的稳定工作范围与不同工况下的效率与膨胀比。3维叶片的控制参数涉及到多叶片型面、叶型积叠线、子午面流道等多个设计变量，每个设计变量需要用多个设计参数表达；而流场计算程序为求解非线性N-S方程组，设计参数与向心涡轮目标气动性能参数之间呈现高度非线性关系，必然为大空间多峰值寻优问题。本文选用的遗传算法（GeneticAlgorithms）是由美国密执安大学Holland教授于提出[13]，20世纪70年代De Jong进行了优化计算[14]，80年代经过Goldberg的归纳总结，形成了遗传算法的基本构架[15]，因其具有并行性、随机性、通用性、全局寻优性强等优点而被广泛应用[12]。

此外，为了比较每次流场计算结果的优劣，将气动参数进行组合设置成目标函数。对于大空间寻优问题，需要采用3维流场计算结果直接计算目标函数。因此在优化过程中需要进行多次3维流场计算，若采用单台计算机优化耗时很长，需采用降低耗时的方案——多CPU并行。

所以数值优化算法采用并行遗传算法，选用主从模式作为遗传算法并行方案，即将服务器节点分成控制节点和计算节点。控制节点用于处理遗传算法的选择、交叉和变异等遗传操作，并将产生的每1代群体个体分组，然后将代表个体的设计参数发送给计算节点。计算节点将设计参数转化成对应叶片，并进行流场计算得到目标函数值，最后将目标函数值返回控制节点。由于设计变量和目标函数数据量很小，以此为通信参数可实现高效率并行优化，智能得到高气动性能的叶片。

1.2 流场数值计算方法

流场数值计算采用Denton黏性体积力方法[12]。该方法在无黏流控制方程中加入黏性体积力项，以考虑流体黏性影响，方程求解计算速度快且具有较高计算精度，因此在叶轮机流场计算中被广泛应用。

1.3 向心涡轮叶片参数化方法

向心涡轮叶片采用基于修改量的参数化方法，即在初始叶片型面、流道和安装角上叠加修改量（实现多变量耦合优化），对修改量采用贝塞尔曲线描述。

该方法的优点是可通过遗传算法变量范围限制实现优化过程生成叶片的可控性和合理性；但条件是需有初始向心涡轮。原有初始向心涡轮共有9个叶片，进口直径为52mm，设计转速为150000r/min，设计流量为0.047kg/s，膨胀比为1.525。

1.4 目标函数设置

本文向心涡轮优化目标是在设计点保持向心涡轮流量、膨胀比与初始涡轮相同，提高轮周效率。由于优化涡轮与初始涡轮的进、出口边界条件相同，因此由进口总压与出口静压确定的膨胀比近似不变，通过权重系数将多目标转化为单目标优化，所以目标函数设置为

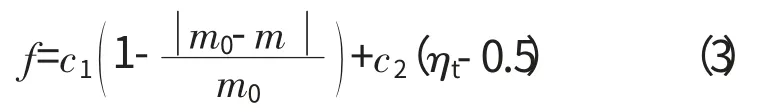
式中：f 为目标函数值；c1、c2为权重系数；m0、m 分别为目标流量、设计叶片流量；ηt为设计叶片的效率。通过多次优化试验，将流量和轮周效率的权重系数c1、c2分别设置为10、400。

由于提高效率较难，所以采用较高的效率权重系数。优化采用试验室服务器16个节点（每个节点8个核），设置每个节点同时进行8个流场计算，每代512个个体，交叉、变异算子分别设置为0.8、0.05。叶片优化设计变量为2条上、下子午面流道曲线，每条曲线有2个设计参数；安装角有2个设计参数；叶片取4个型面，每个型面有吸力面与压力面2条型线；压力面的型线有5个设计变量，吸力面的型线联动以保证型面厚度不变；共20个设计变量。所以，该优化设计共有26个设计参数，最终通过优化结果处理模块输出优化叶片。

2 优化结果分析

向心涡轮气动优化设计流程如图1所示。初始叶片与优化叶片子午面与3维造型的对比分别如图2、3所示。从图2中可见，优化叶片的轮毂线向下移动，机匣线向上移动，子午面通道扩大，涡轮的通流能力增强；上、下子午面均向外平移的同时，叶尖叶根均向外延长，可有效提高向心涡轮叶片的作功能力。

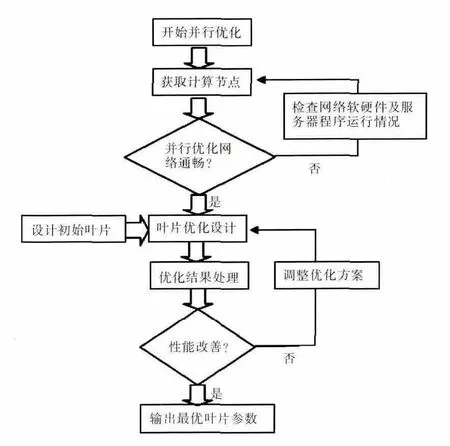
图1 向心涡轮气动优化设计

为了全面分析比较初始与优化叶片气动性能并验证优化结果，本文采用商用软件NUMECA进行数值模拟。向心涡轮叶片网格生成使用NUMECA软件Autogrid5模块，叶片属性为向心、转子，叶尖间隙为0.25mm，设置子午面流道节点数后自动生成网格。

初始与优化叶片的网格数均为40万左右，网格质量均符合计算要求。流场 数值 求 解 使 用Fine/Turbo模块，计算求解运用3维雷诺平均N-S方程，采用中心差分格式，利用4阶Runge-Kutta法进行时间推进，湍流模式选用一方程SA模型，计算残差均收敛在10-5以下。

优化前后向心涡轮的流量与轮周效率特性曲线如图4所示。从图中可见，在整个流量变化范围内，膨胀比变化不大，略有增大；向心涡轮的轮周效率均提高2～3个百分点。

初始与优化叶片在设计工况下（转速为150000 r/min，流量为0.047kg/s）总体性能的比较见表1。从表中可见，优化叶片的轮周效率比初始叶片的提高近3%，流量有小幅度提升，膨胀比近似不变。

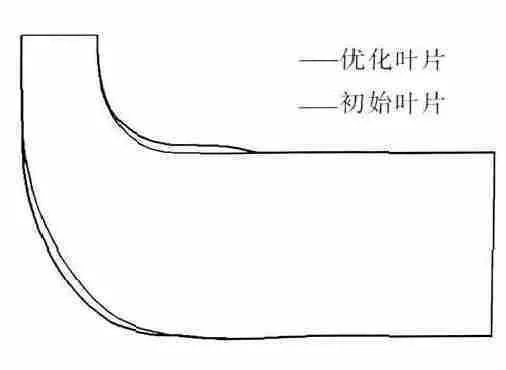
图2 子午面造型比较

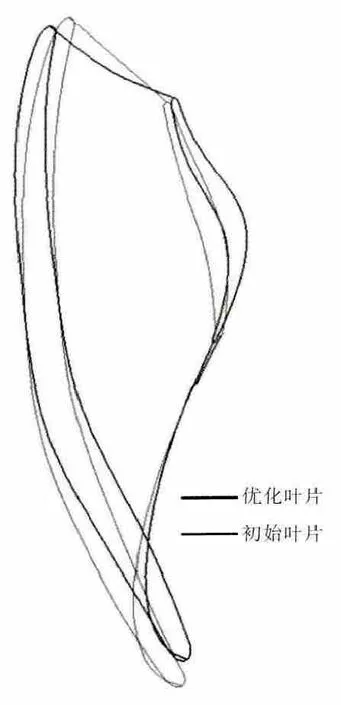
图3 3维造型对比

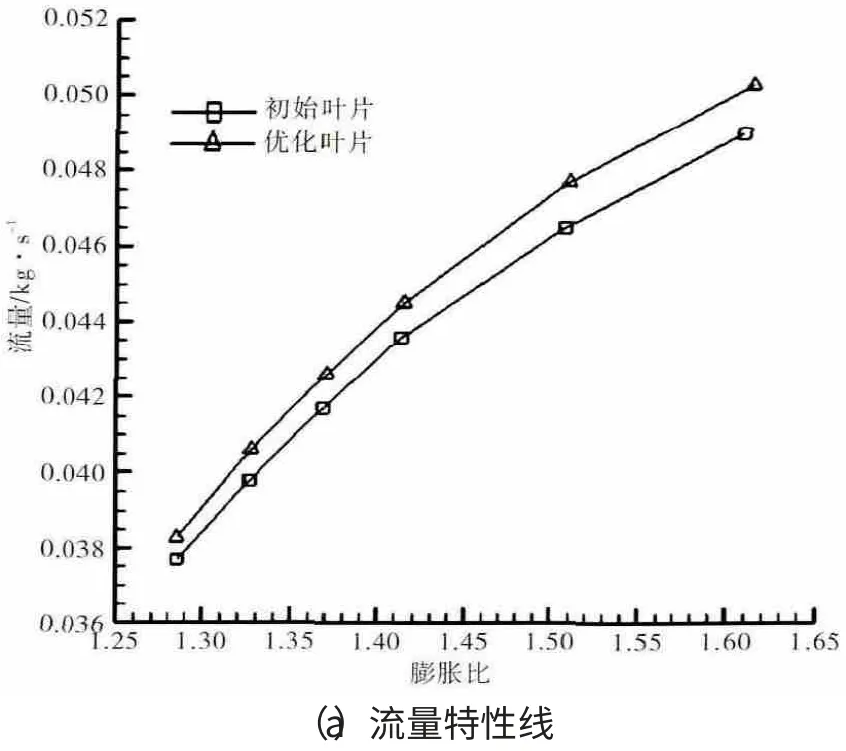
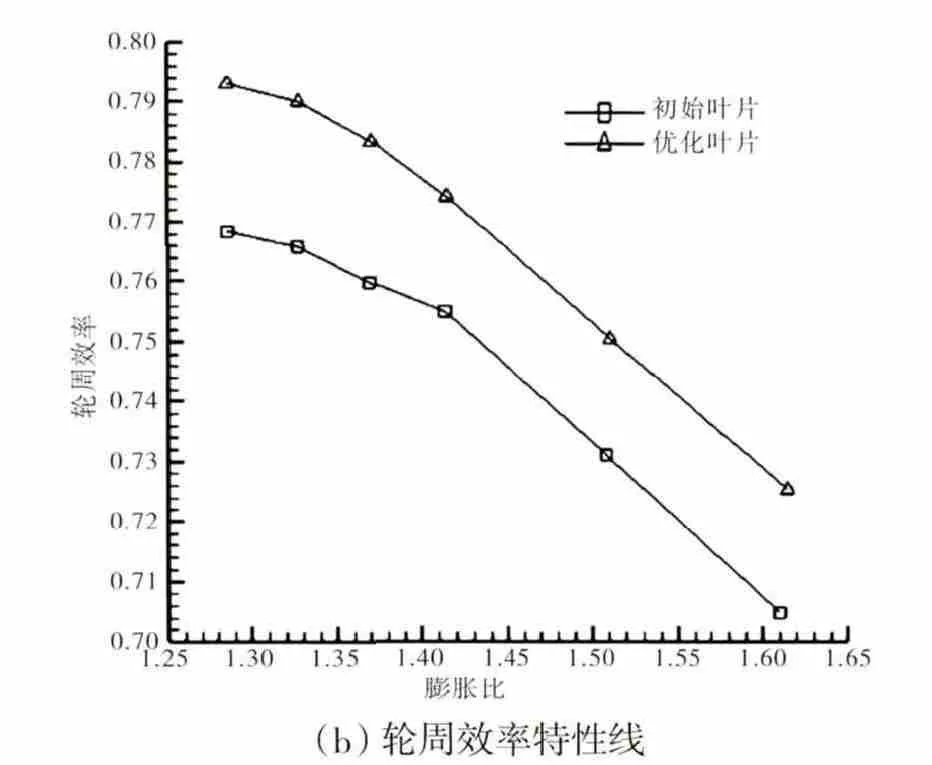
图4 优化前后向心涡轮特性曲线

初始与优化叶片在设计工况下膨胀比与轮周效率沿径向分布对比如图5、6所示。从图中可见，沿径向优化叶片的膨胀比略大于初始叶片的，但增大幅度较小；优化叶片的轮周效率均高于初始叶片的，在60%叶高以上愈加明显，在90%叶高到叶尖部分要高于初始叶片5个百分点以上。因此，向心涡轮在设计工况下的整体性能得到提高。

初始与优化叶片子午面上平均熵值的分布如图7所示。从图中可见，在网格进口至叶片出口熵值差异不大；在网格进口处优化叶片的熵值略小于初始叶片的；在网格出口50%叶高以上均存在高梯度熵区。优化叶片叶尖区域熵值明显小于初始叶片的，这是由于优化叶片上子午面流道近出口区域凸起使得出口处局部收缩有益于抑制叶尖间隙区流动分离，从而减少损失。

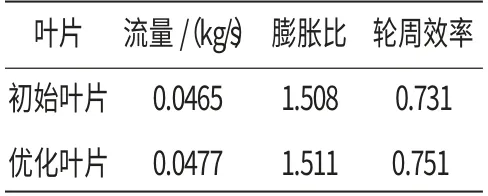
表1 初始叶片与优化叶片设计工况总体性能比较

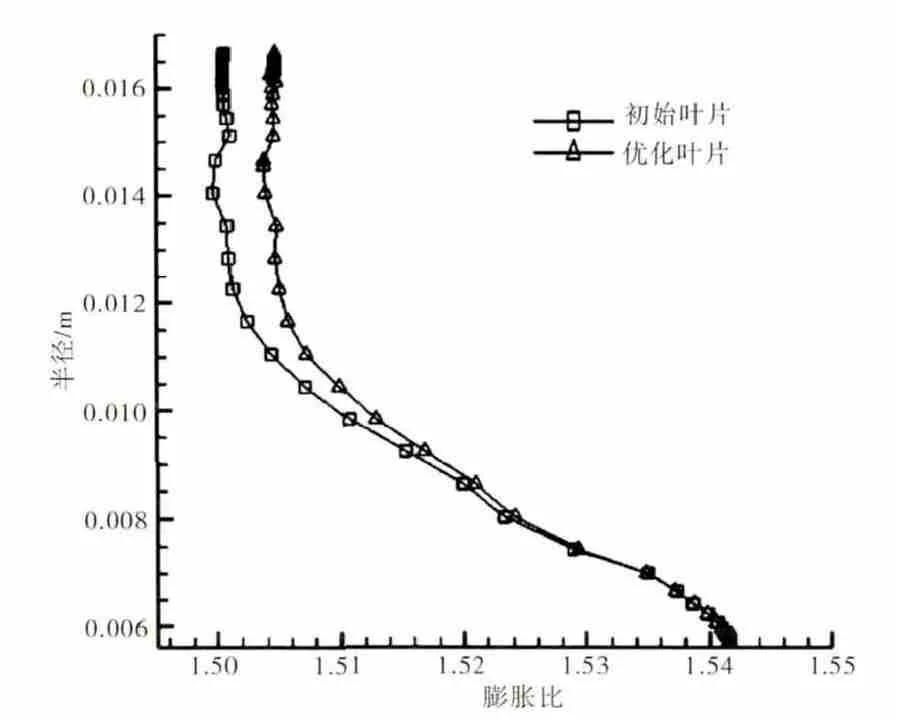
图5 膨胀比沿径向分布

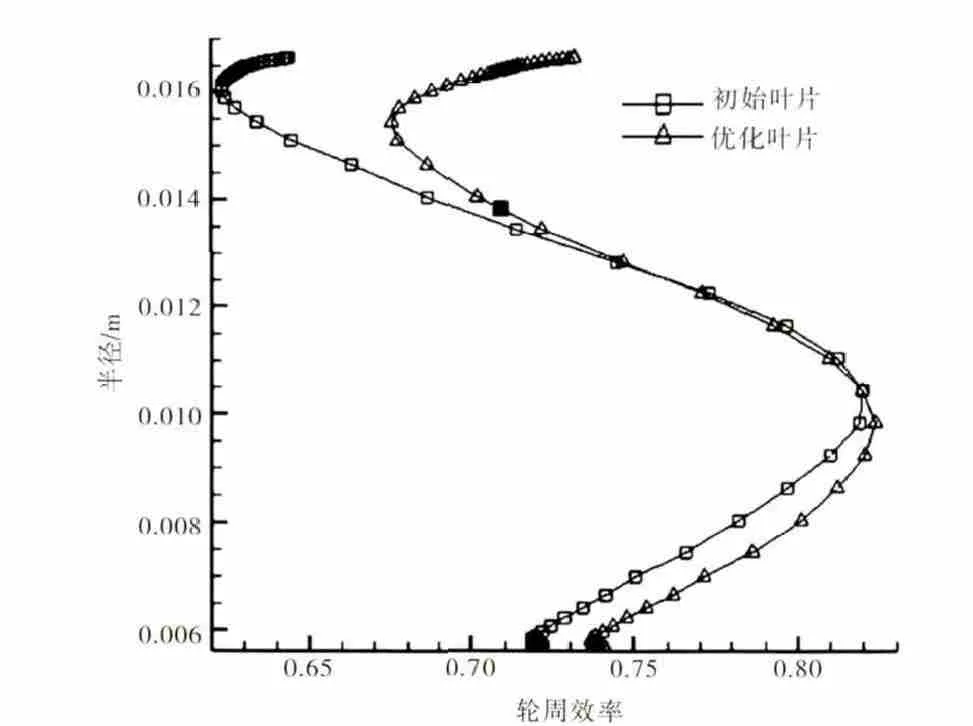
图6 优化前后叶片的膨胀比与轮周效率沿径向分布

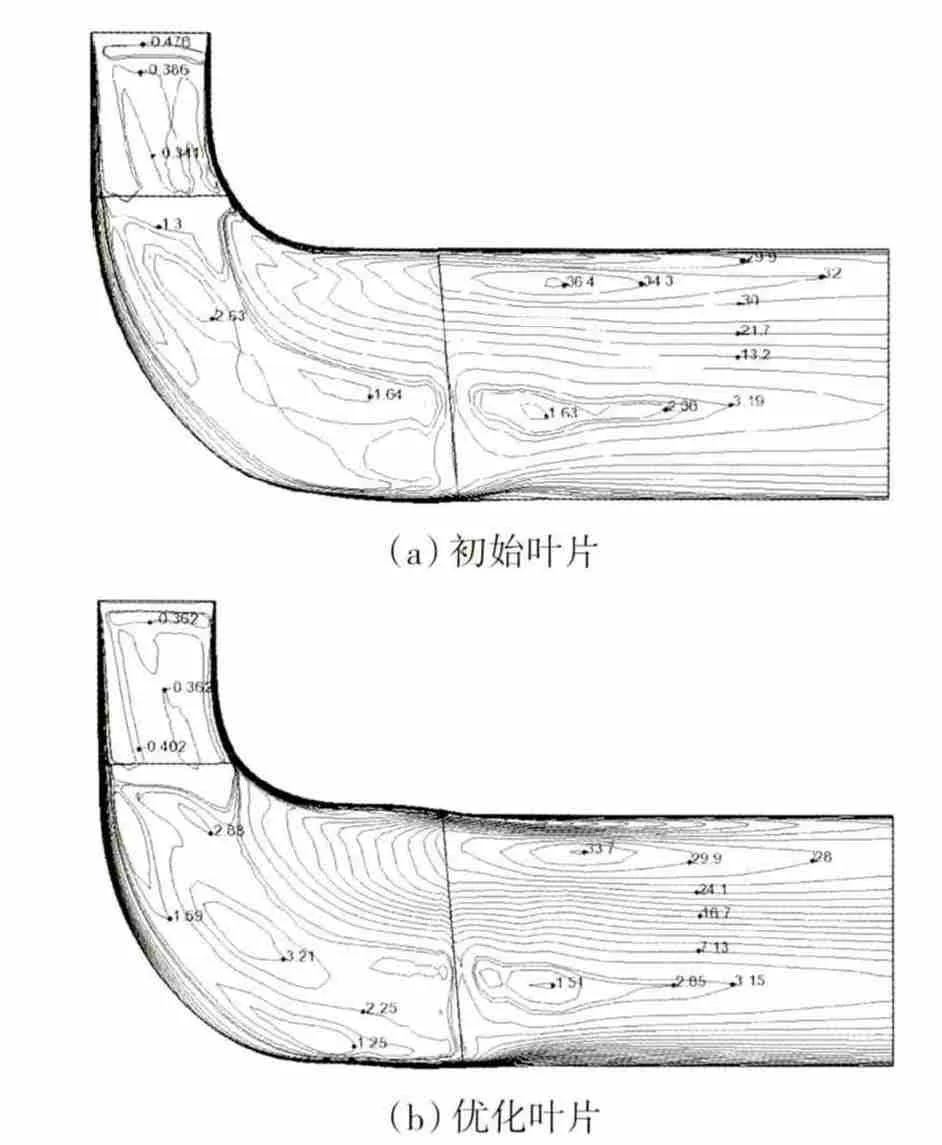
图7 优化前后子午面平均熵值分布

3 结论

（1）采用基于并行遗传算法的向心涡轮气动优化设计方法，解决了小尺寸向心涡轮3维特征显著、造型变量多，设计难以得到高性能的问题。

（2）对设计转速150000r/min、流量0.047kg/s的小尺寸向心涡轮以保持流量、膨胀比不变提高效率为目标进行优化设计，设计点轮周效率提高近3%；非设计工况效率也有近于相同幅度提高。

（3）数值最优化结果表明，本文采用的并行遗传算法不仅可实现多变量耦合优化，而且可高效地得到高气动性能叶片。

[1]Rodgers C.Radial turbines-blades number and reaction effects[R].ASME 2000-GT-0456.

[2]方昌德.航空发动机的发展前景[J].航空发动机，2004，30（1）：1-5.FANG Changde. Prospective development of aeroengines[J].Aeroengine，2004，30（1）：1-5.（in Chinese）

[3]梁德旺，黄国平.厘米级微型涡轮喷气发动机主要研究进展[J].燃气涡轮实验与研究，2004，17（2）：9-13.LIANG Dewang，HUANG Guoping.Recent development and key techniques of micro-turbine in centimeter size [J].Gas Turbine Experiment and Research，2004，17（2）：9-13.（in Chinese）

[4]温泉，梁德旺.微小型向心涡轮转子的流动特性分析[J].内燃机学报，2004，22（3）：265-272.WEN Quan，LIANG Dewang.Flow behavior analysis in a small radial inflow turbine rotor[J].Transactions of CSICE，2004，22（3）：265-272.（in Chinese）

[5]Cox G，Roberts A，Casey M.The development of a deviation model for radial and mixed-flow turbines for use in through flow calculations[R].ASME 2009-GT-59921.

[6]冀春俊，张鹏刚.向心透平内部流动的数值分析及叶轮的改进设计[J].燃气轮机技术，2005，18（2）：44-48.JI Chunjun，ZHANG Penggang.Numerical simulation of the radial flow turbine and impeller modification design[J].Gas Turbine Technology，2005，18（2）：44-48.（in Chinese）

[7]郑振江.高膨胀比向心涡轮的气动设计与数值模拟[D].哈尔滨：哈尔滨工业大学，2011.ZHENG Zhenjiang.Aerodynamic design and numerical simulation of the high expansion ratio radial turbine[D].Harbin：Harbin Institute of Technology，2011.（in Chinese）

[8]杨浩.流动特性对径流式涡轮绝热效率及其测试方法影响的研究[D].北京：北京交通大学，2011.YANG Hao.Numerical investigation on effects of flow behavior on efficiency characteristic and test method in a radial inflow turbine[D].Beijing：Beijing Jiaotong University，2011.（in Chinese）

[9]冯涛，周颖，邹正平，等.向心涡轮内部流动数值模拟分析[J].航空动力学报，2006，21（3）：448-454.FENG Tao， ZHOU Ying， ZOU Zhengping， et al. Numerical simulation of the flow inside radial inflow turbine[J].Journal of Aerospace Power，2006，21（3）：448-454.（in Chinese）

[10]马洪波，朱剑，席平.基于参数化的涡轮叶片三维气动优化仿真[J].计算机仿真，2008，25（10）：27-30.MA Hongbo，ZHU Jian，XI Ping.Aerodynamic 3D optimization simulation of turbine blade based on parametric design[J].Computer Simulation，2008，25（10）：27-30.（in Chinese）

[11]周文哲，杨策，陈山，等.径流式涡轮三维叶型优化设计[J].车辆与动力技术，2009（4）：1-5.ZHOU Wenzhe，YANG Ce，CHEN Shan，et al.Optimization on a 3D blade shape of radial turbine[J].Vehicle&Power Technology，2009（4）：1-5.（in Chinese）

[12]汪光文.基于并行遗传算法风扇/压气机叶片气动优化设计[D].南京：南京航空航天大学，2009.WANG Guangwen.Research on aerodynamic optimization design of fan/compressor blade using parallel genetic algorithm [D].Nanjing:Nanjing University of Aeronautics and Astronautics，2009.（in Chinese）

[13]Holland J H.Adaptation in natural and artificial systems[M].Cambridge：MIT Press，1992：171-198.

[14]De Jong K A.An analysis of the behavior of a class of genetic adaptive systems[D].Ann Arbor:University of Michigan，1975.

[15]Goldberg D E.Genetic algorithms in search，optimization and machine learning[M].Boston：Addison Wesley，1989：218-260.