不同接触形式下轮盘叶片系统的振动响应分析

王 迪，吴志渊，能海强，马 辉

（东北大学机械工程与自动化学院，沈阳110819）

0 引言

旋转轮盘叶片结构的振动和叶片振动疲劳损伤故障一直是透平机械中较为严重的问题。盘片系统在工作时，受离心载荷和非稳态气流激振力等复杂载荷的共同作用产生强迫振动，而轮盘榫槽与叶片榫头的接触面连接，起传递载荷和约束定位的双重作用，在一定程度上影响盘片系统的振动特性。

按照研究目的的不同，对盘片系统的振动特性研究主要分为榫槽-榫头的接触动力学特性分析[1-5]，以及在此基础上开展的接触疲劳和微动疲劳研究[6-7]；考虑榫槽-榫头接触连接或刚性连接，进行盘片耦合系统的固有频率及耦合振型分析[8-11]；考虑榫根和叶冠干摩擦阻尼，进行盘片耦合系统的共振频率及强迫振动响应分析[12-13]。

从上述文献分析可知，关于接触对固有特性的影响的研究较多；对榫槽-榫头接触的研究多限于静态接触特性分析；关于接触对振动响应的影响研究较少。基于这一情况，本文运用ANSYS软件分析了榫槽-榫头接触、不分离接触和刚性连接3种不同接触面约束形式，对盘片系统固有特性及振动响应的影响。

1 旋转叶片振动的有限元动力学方程

旋转叶片振动的动力学方程为

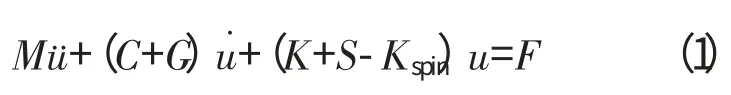
令C1=C+G，K1=K+S-Kspin，则旋转叶片的动力学方程可简化为

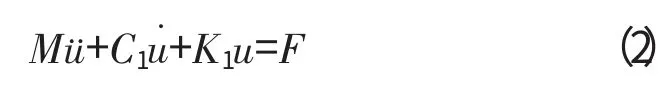
采用谐响应分析，求解不同转速下系统在气动激振力作用下的振动响应

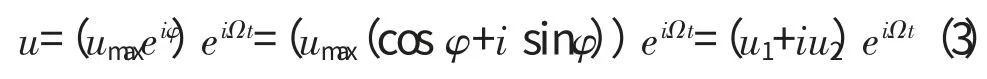
式中：umax为最大位移向量；i 为虚数单位；φ 为位移相位角；Ω=2πf，f 为气动力激振频率。

式中：Fmax为最大激振力向量；ψ 为激振力相位角。

将式（3）和（4）代入式（2）得

基于ANSYS软件，采用完全法求解式（5），获得系统随转速变化的幅频响应曲线。考虑旋转离心力所导致的离心刚化，在进行谐响应分析前应先考虑对离心力进行静力分析。

2 盘片结构固有特性分析

2.1 盘片结构有限元模型

本文基于ANSYS有限元软件，建立了3种有限元模型：考虑接触面的分离、滑移和黏合等影响的榫槽-榫头接触模型；接触面和目标面接触后相连接，考虑接触面的相对滑动和黏合等影响的榫槽-榫头不分离接触模型；榫槽-榫头接触面绑定的刚性连接模型。

模型为中心对称结构，因此选取整周模型1/38扇形区中的单个叶片进行建模，其结构和有限元模型如图1所示。为了更好地模拟接触，对榫槽和榫头接触区域的网格进行了细化（放大如图1（b）所示）。三者接触面部分的差异如图2所示。

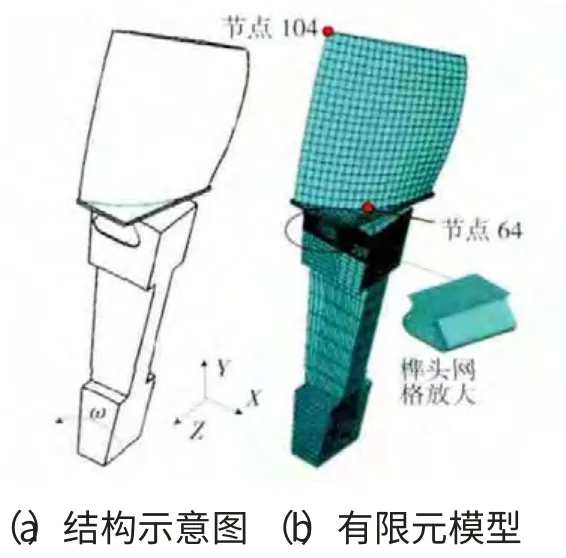
图1 盘片结构与有限元模型

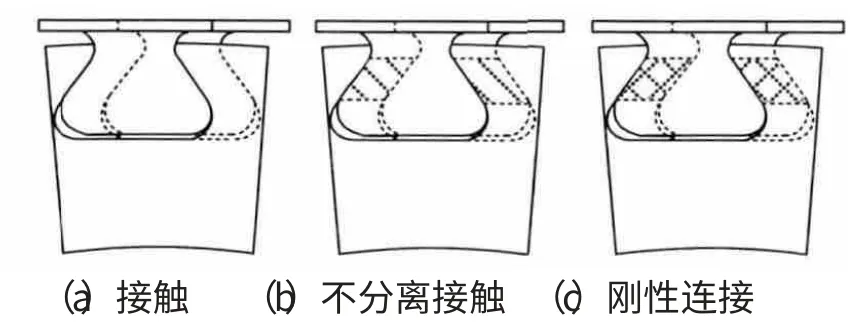
图2 盘片接触面模型

本文所选用盘片系统的材料参数如下：叶片的弹性模量E=1.25×1011Pa，密度ρ=4370kg/m3，泊松比υ=0.3。采用Solid186实体单元，对盘片模型进行网格划分，其中有限元模型共划分22948个单元和89943个节点。接触面设定为Conta174单元、目标面设定为Targe170单元。

2.2 固有特性分析

考虑到离心刚化、旋转软化以及科氏力对固有特性的影响，根据不同转速下的各阶固有频率绘制Campbell图，如图3所示。由于上游静子叶片数为42片，因此转子每转1周受到42次尾迹气流激振力，所以激励线的谐波数K=42，其斜率为42/60。在Campbell图中激励线与各阶动频交点为潜在的共振频率点，各阶共振频率下的振型图如图3所示。

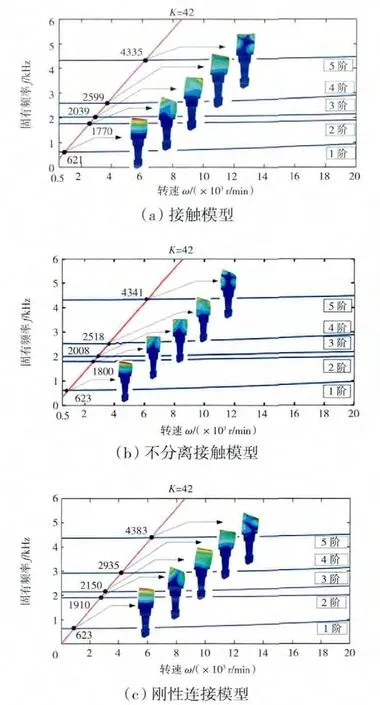
图3 3种模型的Campbell图及振型

从图3中可见，接触与不分离接触模型的第1、2和4阶的共振频率和振型吻合较好，刚性连接模型的振型只有第1、2阶与另2种模型的振型接近，高阶振型相差较大，并且刚性连接模型与2种接触模型的共振频率差距较大。3种模型的前5阶共振频率见表1。

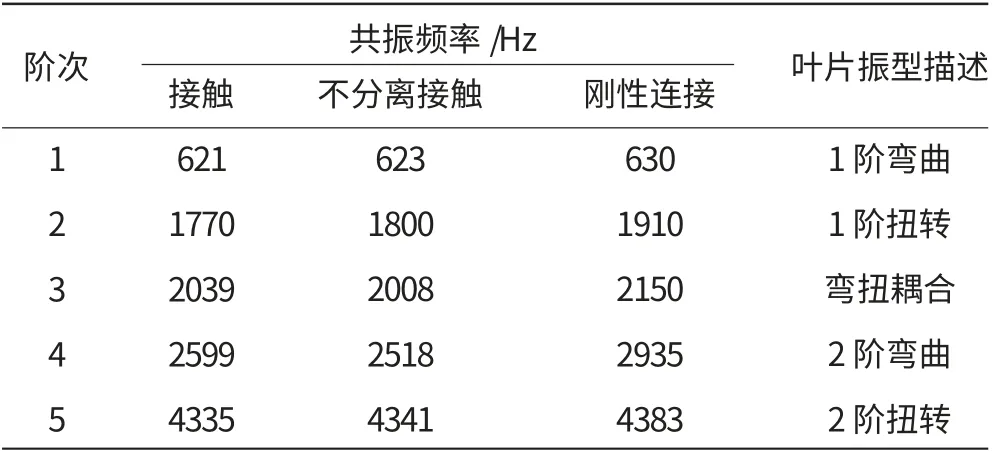
表1 3种模型共振频率对比

3 盘片结构振动响应分析

叶片故障的统计分析表明，叶片的损坏多由叶片振动的动应力过大引起，而影响叶片动应力的主要因素是离心力和非稳态气流激振力[14]。因此，需要对盘片系统在气流激振力作用下的振动响应进行分析。叶片表面的气流激振力可简化为周期性的正弦激振力[15]

式中：A0为转子叶片表面的定常压力值；A1为转子叶片表面的压力脉动幅值；N=42，为转子前排静子叶片数；ω 为转速(r/min)；φ 为相位角。

本文不考虑定常压力值的影响，即假定A0=0。叶片存在叶盆和叶背2个面，2个面的脉动幅值A1分别取0.20MPa和0.16MPa。

在计算响应之前首先需要确定系统的阻尼，本文采用比例阻尼(Rayleigh)模型

式中：ω1、ω2分别为系统的第1、2阶固有角频率；ξ1、ξ2分别为系统的第1、2阶模态阻尼比，本文取ξ1=ξ2=0.04。

在ANSYS软件中采用谐响应分析来计算系统的幅频振动响应，在计算过程中考虑旋转导致的离心刚化、旋转软化和科氏力的影响，并在扫频时考虑气体激振力频率和转频存在的N倍关系。主要选择了叶盆面上的2个位置来对比接触模型、不分离接触模型和刚性连接模型的仿真结果，所提取的节点位置如图1（b）所示。

考虑气动力作用，接触模型在低转速下很难收敛，因此将接触模型的起始气动力频率调整为1200Hz。经过分析可知3种模型都在叶根处（节点64）的等效应力最大，其幅频响应曲线如图4所示。其中，图4（a）为整个频率段处的最大等效应力，图4（b）为局部放大。从图中可见，3种模型的动应力随频率的变化趋势相近，且接触模型与不分离接触模型的动应力几乎相同。刚性连接模型与不分离接触模型在中低频段(f<5000Hz)的动应力幅值相近，且在第1、2第4阶固有频率处发生共振。在第1阶固有频率处发生的共振最危险，刚性连接与接触模型在高频段（f>5000Hz）存在较大差异，由三者的共振峰位置可知，刚性连接模型共振频率要大于接触模型的。分析最大等效动应力可得：在低频段时接触模型计算不收敛，第1阶共振时的最大动应力不易测出，所以在低频段可以用不分离接触模型近似代替接触模型进行振动响应分析。

图4 叶根处最大等效应力幅频响应曲线（节点64）

经过分析可知，3种模型的合位移幅值最大值均在叶尖处（节点104），其合位移幅频响应曲线如图5所示。图5（a）为整个频率段的位移幅频响应曲线，图5（b）为局部放大。从图中可见，接触模型与不分离的接触模型在整个频率段都较为相近。与最大等效应力幅频响应规律类似，在中低频段（f<5000Hz）刚性连接模型与不分离接触模型的变化规律相似；在高频段（f>5000Hz）二者的幅值存在较大差异，且随气动力频率增加差距增大。刚性连接模型与接触模型在高频段的动应力和幅值差别较大，为了在高频段时得到准确的结果，必须考虑接触的影响，不能用刚性连接模型来代替接触模型。盘片系统在第1、2和4阶处发生共振，且在第1阶时振幅最大、破坏性也最大。在低频段接触模型计算不易收敛，第1阶共振不易被发现，所以在低频段计算时可采用不分离接触模型或刚性连接模型来代替接触模型。

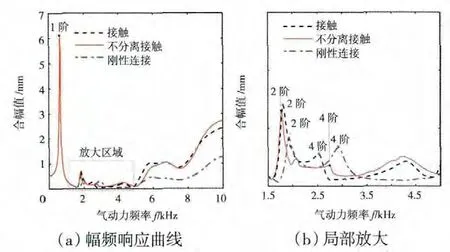
图5 叶尖处位移幅频响应曲线（节点104）

叶片在节点104处x、y 和z 3个方向上的位移幅频响应曲线如图6所示。从图中可见，叶片的轴向振幅（z 向）和切向振幅（x 向）较大，径向振幅（y 向）较小，故叶片合幅值的变化主要受轴向幅值和切向幅值影响。由于叶片存在一定的扭转角，在气动激振力作用下会产生轴向弯曲和径向弯曲，所以在盘片系统设计中要注意叶片在轴向和径向的振动。

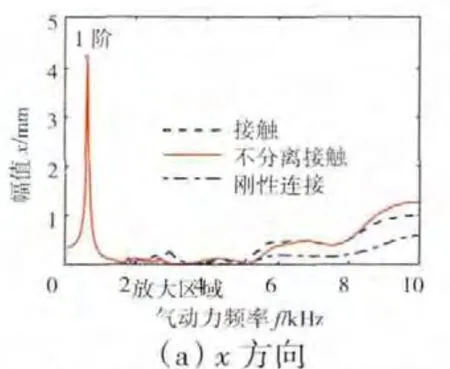
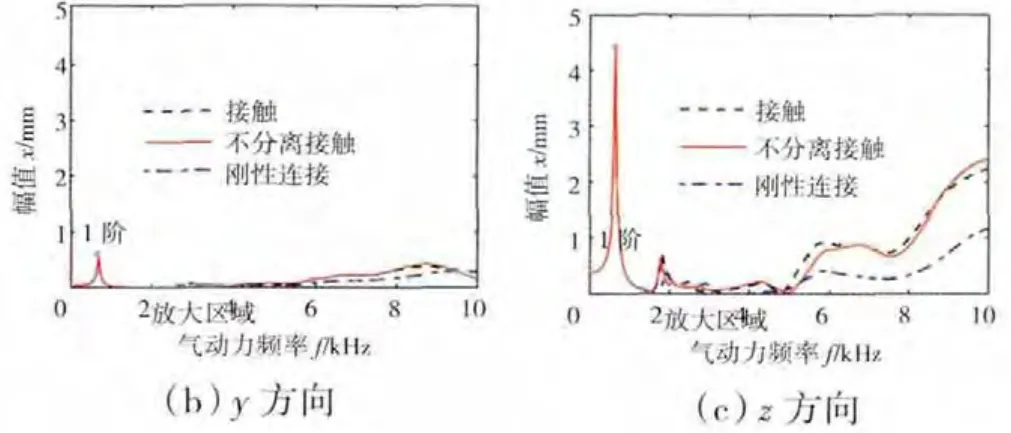
图6 叶尖处3个方向的幅频响应对比（节点104）

由上述分析可知，刚性连接模型的振动响应与接触模型和不分离接触模型的存在一定差别。在高频段，接触模型的位移幅值与动应力幅值大于刚性连接模型的，而接触模型和不分离接触的模型在整个频率段具有较好的一致性，刚性连接模型和不分离接触模型在中低频段一致性较好。盘片系统在第1阶固有频率处发生共振，且此时等效动应力和位移幅值最大，盘片系统破坏也最为严重。但是接触模型在低频段（f<1200Hz）下计算不易收敛，第1阶共振特性不易被发现。因此可以适当选用不分离接触模型或刚性连接模型来近似分析盘片系统在低频段的振动响应。

4 结论

基于ANSYS有限元软件，建立了3种有限元模型：接触模型、不分离接触模型和刚性连接模型。对比三者固有特性以及振动响应，得到以下结论：

（1）接触模型和接触不分离模型的固有特性吻合较好，但与刚性连接模型的相差较大。

（2）刚性连接模型与不分离接触模型在中低频段一致性较好，而在高频段存在较大差异；接触模型与不分离接触模型在整个频率段一致性较好。盘片系统在第1、2和4阶固有频率处发生共振。

（3）由于不分离接触模型和刚性连接模型能够弥补接触模型在较低转速下考虑气动力计算不收敛的问题，因此在理论研究中，可以适当地选用2种模型来近似分析盘片系统在低转速下的振动响应。

[1]Papanikos P，Meguid S A，Stjepanovic Z.Three-dimensional nonlinear finite element analysis of dovetail joints in aeroengine discs[J].Finite Elements in Analysis and Design，1998，29（3）：173-186.

[2]Beisheim J R，Sinclair G B.On the three-dimensional finite element analysis of dovetail attachments[J].ASME Journal of Turbomachinery，2003，125（2）：372-379.

[3]Sinclair G B，Cormier N G，Griffin JH，et al.Contact stresses in dovetail attachments:finite element modeling [J].ASME Journal of Engineering for Gas Turbines and Power，2002，124（1）：182-189.

[4]魏大盛,王延荣.榫连结构接触面几何构形对接触区应力分布的影响[J].航空动力学学报，2010，25（2）：407-411.WEI Dasheng，WANG Yanrong.Effects of profile of contact surfaces on the stress distribution for tendon jointing in blade disk assemblies[J].Journal of Aerospace Power，2010，25（2）：407-411.(in Chinese)

[5]Anandavel K，Prakash R V.Effect of three-dimensional loading on macroscopic fretting aspects of an aeroengine blade-disc dovetail interface[J].Tribology International，2011，44（11）：1544-1555.

[6]Wei D S，Wang Y R，Yang X G.Analysis of failure behaviors of dovetail assemblies due to high gradient stress under contact loading[J].Engineering Failure Analysis，2011，18（1）：314-324.

[7]Golden P J，Calcaterra J R.A fracture mechanics life prediction methodology applied to dovetail fretting [J].Tribology International，2006，39（10）：1172-1180.

[8]王春洁，宋顺广，宗晓.压气机中叶片轮盘耦合结构振动分析[J].航空动力学学报，2007，22（7）：1065-1068.WANG Chunjie，SONG Shunguang，ZONG Xiao.Vibration analysis of the blade-disc coupled structure of compressor [J].Journal of Aerospace Power，2007，22（7）：1065-1068.(in Chinese)

[9]张原，郁大照，张浩然.自由涡轮叶片-轮盘耦合振动特性分析[J].航空发动机，2011，37（6）：21-25.ZHANG Yuan，YU Dazhao，ZHANG Haoran.Analysis of coupled vibration characteristics of free turbine blade/disk [J].Aeroengine，2011，37（6）：21-25.(in Chinese)

[10]Qin F，Chen L M，Zhang X F，et al.Fundamental frequencies of turbine blades with geometry mismatch in fir-tree attachments[J].Journal of Turbomachinery，2006，128（3）：512-516.

[11]孟庆迪，罗贵火.某型发动机涡轮盘整体振动模态的有限元分析[J].振动工程学报，2004，17（1）：113-115.MENG Qingdi，LUO Guihuo.FEA of vibration model of the turbine[J].Journal of Vibration Engineering，2004，17（1）：113-115.(in Chinese)

[12]Petrov E P.Method for sensitivity analysis of resonance forced response of bladed disks with nonlinear contact interfaces[J].Journal of Engineering for Gas Turbines and Power，2009，131（2）：1-9

[13]Petrov E P，Ewins D J.Effects of damping and varying contact area at blade-disk joints in forced response analysis of bladed disk assemblies[J].Journal of Turbomachinery，2006，128（2）：403-410.

[14]李录平,吕振梅,黄文俊,等.静叶尾迹流引起的气流激振力计算方法与激振力特性研究[J].汽轮机技术，2007，49（5）：326-329.LI Luping，LYU Zhenmei，HUANG Wenjun，et al.Research on calculation methods and features of steam exciting force caused by state blade trailing wake [J].Turbine Technology，2007，49（5）：326-329.(in Chinese)

[15]郑娟丽.航空发动机叶片气动激励的相关振动响应研究[D].南京:南京航空航天大学，2009.ZHENG Juanli.Research on vibration response of blade caused by aerodynamic force in aeroengine [D].Nanjing：Nanjing University of Aeronautics and Astronautics，2009.(in Chinese)