某型发动机可靠性环境因子分析及应用

武晓龙，孙 波，尹国武，周祥亮

（1.海军驻沈阳地区发动机专业军事代表室，沈阳110043；2.海军91911部队，海南三亚572000）

0 引言

中国于20世纪80年代引进某型涡轴发动机，现已装备于某型直升机。该型发动机的故障率较高，在规定翻修寿命期内多次发生故障，需要提前更换发动机或单元体。需要从2方面着手解决上述问题：一是通过对发动机主机故障数据进行分析，建立基于Van Montfort方法的威布尔分布检验模型，用于判定发动机使用数据是否服从威布尔分布，从而确定发动机主机的可靠度函数和故障率函数，评估其使用可靠性水平；二是建立可靠性环境因子分析模型，在分布同族性假设成立且失效机理相同的情况下，结合另一单位同型发动机寿命数据，对发动机主机的可靠性环境因子进行研究，从而确定沿海高盐高湿的环境对发动机寿命的具体影响。

本文从上述2方面建立计算模型，对发动机整机可靠性和环境因子开展了研究，并对使用单位和生产单位提出了提高发动机使用可靠性的建议。

1 主机使用可靠性分析

1.1 数据搜集

搜集某单位20台发动机首次故障数据，根据数据筛选原则[1]，对数据进行处理，剔除由其它部附件引起的2次故障和人为因素造成的故障的数据4个，得到有效样本数为16（如发动机到寿，则将其到寿时间800 h列为首次故障时间），删除比为0.2，小于0.5，该组数据有效。某型发动机主机首次故障有效数据见表1。

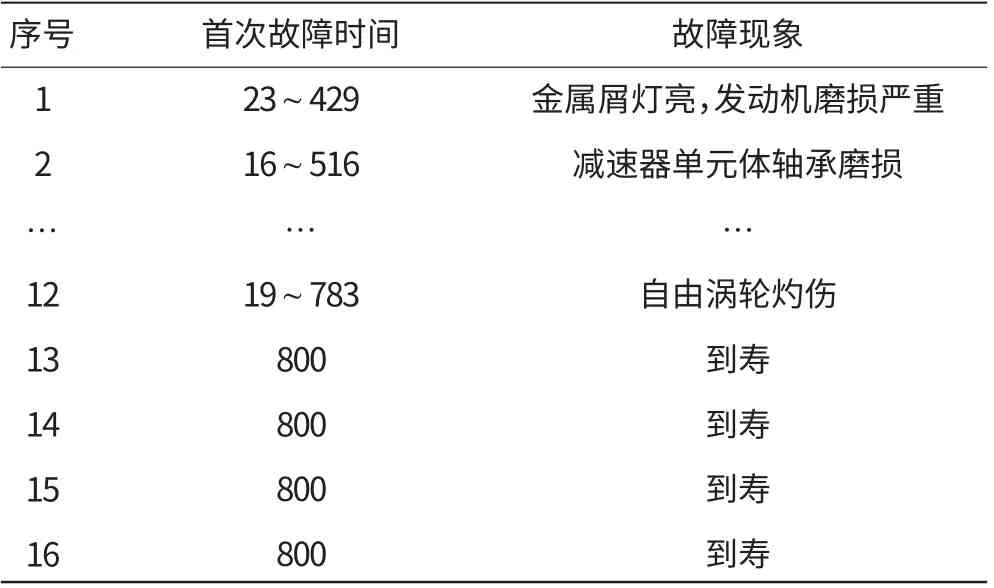
表1 某型发动机主机首次故障有效数据

利用假设检验和参数估计的方法确定样本数据所服从的分布函数及其参数，最终得到发动机使用故障样本数据所具有的统计规律性。本文主要采用寿命分布函数进行使用可靠性分析。

1.2 拟合分布检验

用Matlab编程对表1中的主机故障数据分别进行威布尔分布、指数分布和正态分布拟合，得到主机寿命分布拟合曲线，如图1所示。

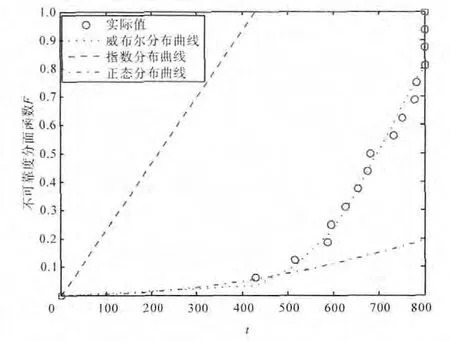
图1 主机寿命分布拟合曲线

从图中可见，主机故障数据能较好地服从威布尔分布。建立基于VanMontfort方法的分布检验模型对发动机主机使用数据进行分布检验。其基本原理如下：

设发动机的寿命分布服从威布尔分布F（t），检验假设

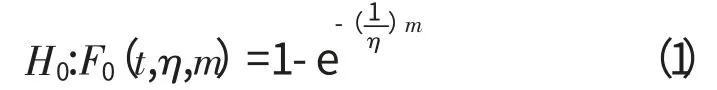
式中：η,m 为未知参数。

r个发动机的失效时间分别为t1≤t2≤…≤tr，假设

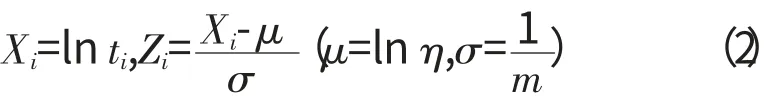
在原假设H0成立的情况下，X1≤X2≤…≤Xr为极值分布的前r个次序统计量。Z1≤Z2≤…≤Zr为标准极值分布的前r个次序统计量，且E（Zi）（i=1,2,…r）有据可查。根据VanMontfort方法提出统计量

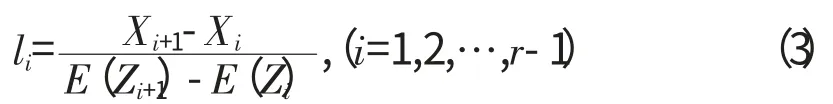
设li渐进独立，且服从标准指数分布，取这里[]为取整符号，所取整数小于或等于括号内值的最大值。则统计量

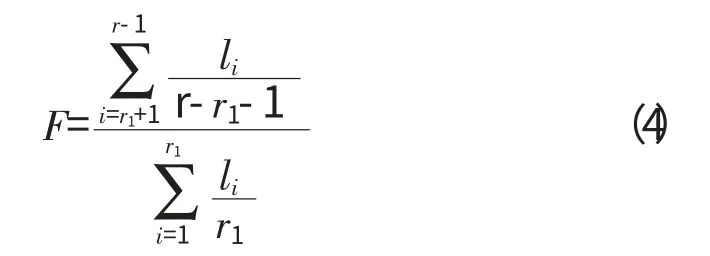
在原假设H0成立条件下，渐进服从自由度为（2（r-r1-1）,2r1）的F 分布，其取值不能过大或过小，对于给定的显著性水平α 的检验规则为F ＜F1-α/2（2（r-r1-1）,2r1）或F>Fα/2（2（r-r1-1）,2r1）时，拒绝H0；F1-α/2（2（r-r1-1）,2r1）≤F≤Fα/2（2（r-r1-1）,2r1）时，接受H0。

在基于VanMontfort方法的分布检验模型的具体算例中，首先假设

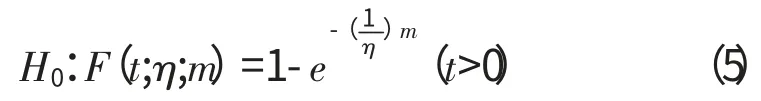
根据VanMontfort方法对发动机使用数据进行计算，分布拟合检验值见表2。

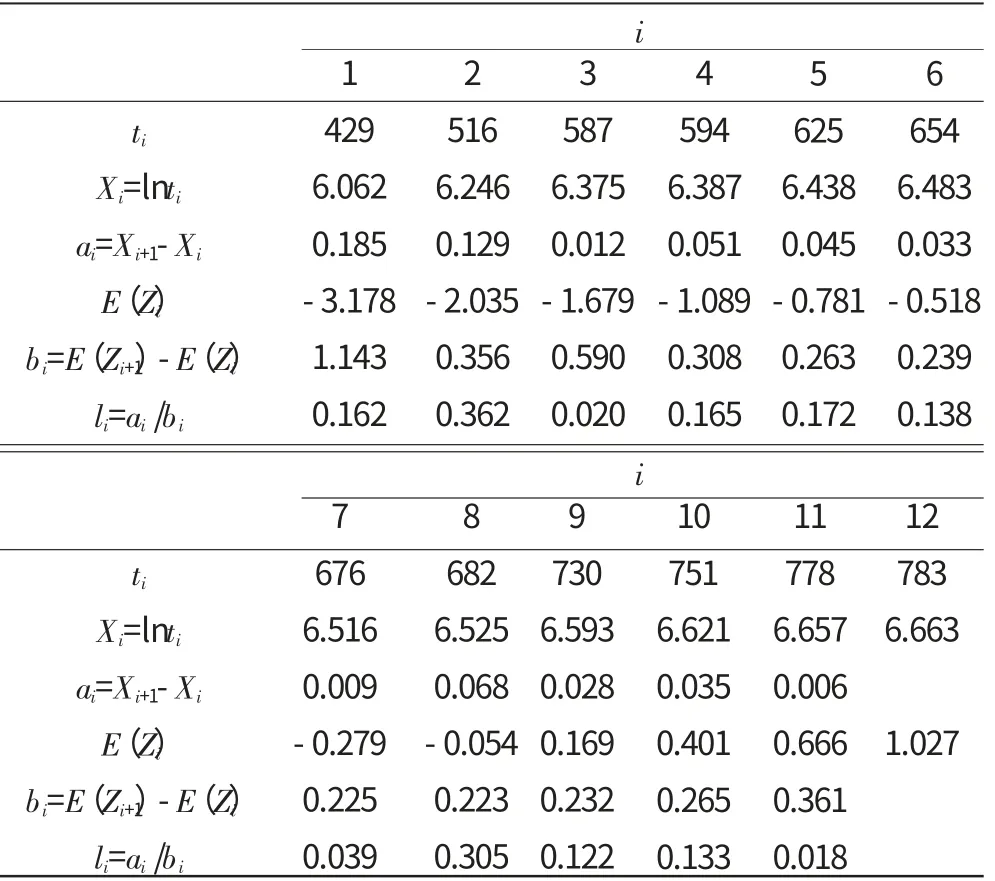
表2 分布拟合检验值

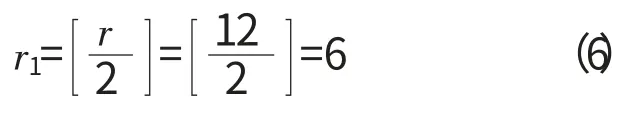
按照VanMontfort方法计算统计量，根据li值可计算F 的观察值，则

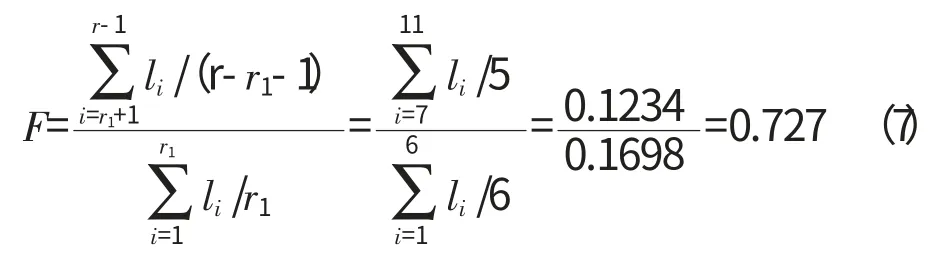
若取显著性水平α=0.1，依F 分布表可得检验临界值

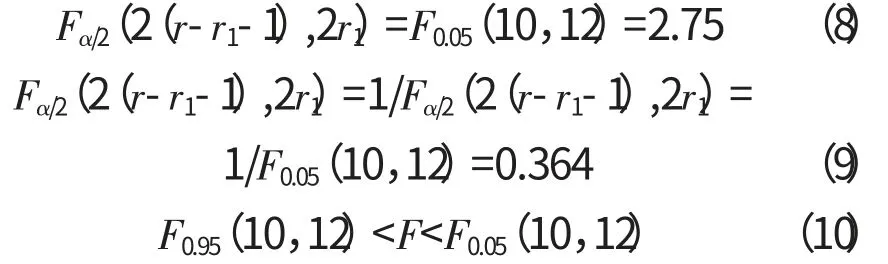
由式（10）判断原假设成立，可认为该型发动机主机服从威布尔分布。采用高精度的最小二乘法[2]计算威布尔分布参数，见表3。

表3 主机首次故障数据处理结果

由此得到主机威布尔分布函数为

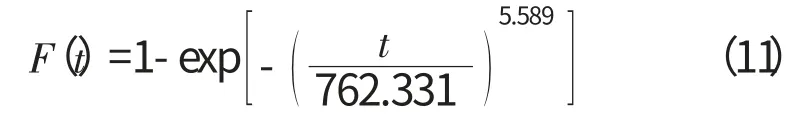
可以计算出发动机主机威布尔分布的平均寿命

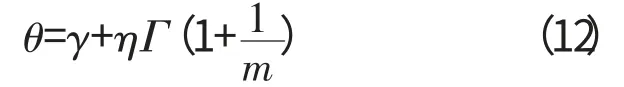
式中：θ 为平均寿命；γ 为位置参数；η 为尺度参数；m 为形状参数函数。

将数值代入

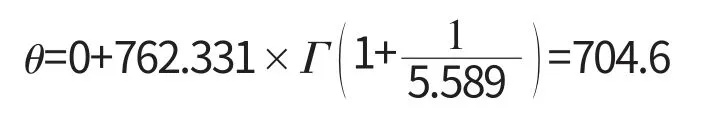
该型发动机的首翻期给定值大于上述值，由此可反证该型发动机在沿海环境的使用条件下其可靠性不高。

给定任务时间Δt=2h，任务可靠度R*（t）=0.98，则

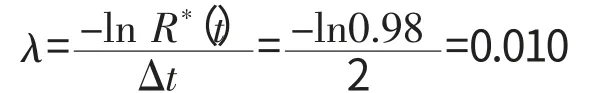
则首翻基值

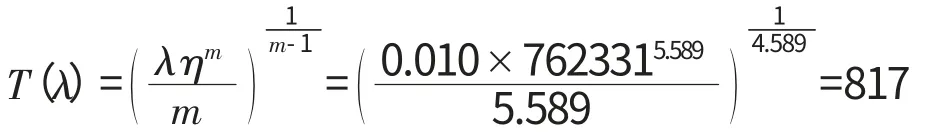
98%的任务可靠度偏低，若适当增大,取任务可靠度R*（t）=0.99时，则

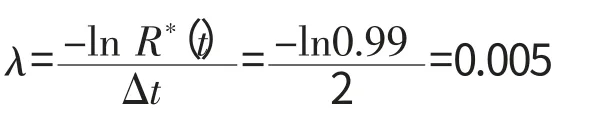
则首翻基值

计算得到的首翻基值远低于给定值。其可能因素为：发动机主机固有可靠度不高；沿海高温高盐高湿的环境对发动机可靠性产生影响。此外，还需对比分析其他地区的发动机使用情况（即研究发动机主机的可靠性环境因子）。

2 发动机主机可靠性环境因子分析

2.1 环境因子分析约束条件

环境因子是表征相同产品在不同环境下失效快慢程度的1个参数，反映了环境对产品可靠性影响的严酷等级[3]。对可靠性环境因子进行分析的约束条件有分布同族假设、机理一致性假设以及Nelson假设[4]。

（1）失效机理一致性假设。在不同应力水平S1，S2，…，Sk下，产品的失效机理保持不变。该假设是研究环境因子相关问题的前提，只有在失效机理保持一致的情况下才能进行不同应力水平下可靠性信息的折算与综合，环境因子的研究才有意义。

（2）分布同族性假设。在不同应力水平S1，S2，…，Sk下，产品的寿命服从同一形式的分布。不同应力水平下的寿命数据的分布形式相同，仅在分布参数上存在差异。可通过分布拟合来检验寿命分布同族性。

（3）Nelson假设。产品的残存寿命仅依赖于已累积的失效和当前应力，而与累积方式无关。这一假设由Nelson提出，实际是将累积失效概率作为环境对产品损伤作用的外在表现，认为即使在不同环境下，只要产品的累积失效概率相同，产品中累积的损伤也相同，即在不同应力水平下作用不同时间的效果相当。

搜集另一使用单位该型发动机使用数据，对某型发动机主机的环境影响因素进行分析。2单位发动机除气候环境差异外，使用、维护水平均相当。用相同方法进行分析的结果表明：其发动机主机寿命数据也服从威布尔分布。

因此，2单位的发动机寿命数据分布同族性假设成立。失效机理一致性假设通过以下方式验证。对于2个威布尔分布而言，当其形状参数相等，即m1=m2=m 时，说明其失效机理一致[5]。

2.2 威布尔形状参数检验方法

设1批发动机主机的寿命T1服从威布尔分布，其分布函数为

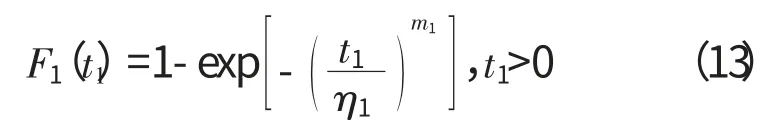
式中：m1、η1为未知参数。

另1批发动机主机的寿命也服从威布尔分布，其分布函数为

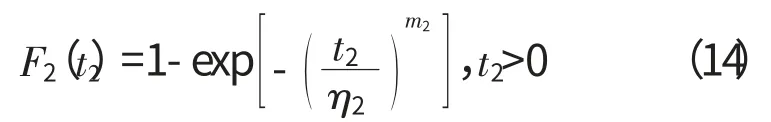
式中：m2、η2为未知参数。

检验假设H0：m1=m2，分析2批发动机主机的形状参数是否相等。对2批发动机主机的寿命T1、T2作变换x=lnT1，y=lnT2，则x 和y 都服从极值分布，其分布函数分别为

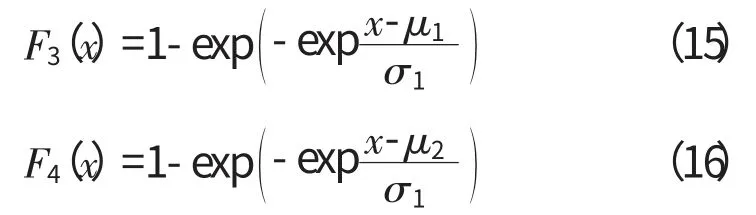
为检验假设是否成立，从母体T1和T2独立地抽取n1和n2个样本，进行定数截尾寿命试验后可得2个独立的截尾子样t11≤t12≤…≤t1r1和t21≤t22≤…≤t2r2，经变换xi=lnt1i，yi=lnt2i，分别可得极值分布F3（x）和F（4x）的截尾子样x1≤x2≤…≤xr1和。

样本量n1<25，n2<25，因此只能采用最优线性无偏估计[8]对数据进行处理。μ1的最优线性无偏估计为

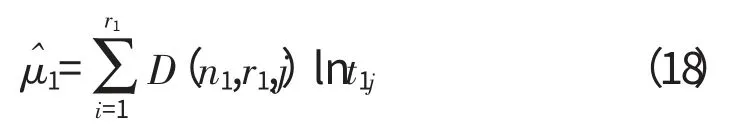
σ1的最优线性无偏估计为

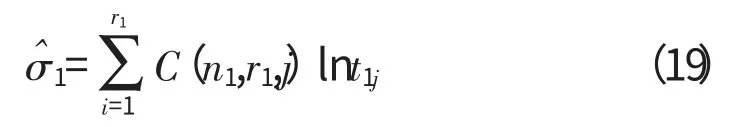
式中：D（n1,r1,j）和C（n1,r1,j）为无偏系数，其值可由最优线性无偏估计表中查到。

同理可得μ2，σ2的最优线性无偏估计。

由σi的最优线性无偏估计的性质可知

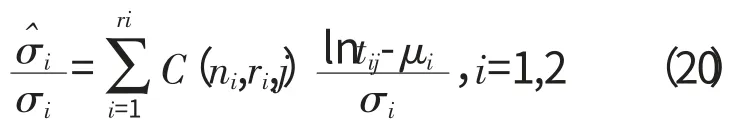
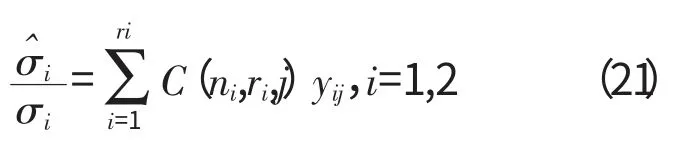
当H0：σ1=σ2成立时

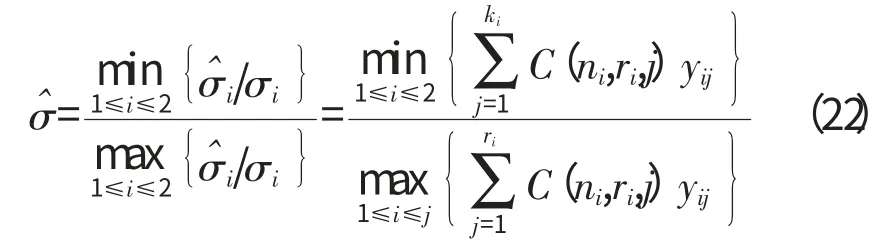
给出显著性水平α 后可求出Cα。使

综上，可对H0进行检验：当统计量σ^的观察值大于Cα时接受H0，否则拒绝H0。

利用威布尔形状参数检验方法对发动机主机形状参数进行检验的具体算例进行分析。设某单位编号为1，该机场发动机寿命数据的总数视为16，有12个失效数据为定数截尾数据，r1=12，且有t11=429,t12=516,…，t112=783；另一单位编号为2，该机场发动机寿命数据总数视为12，有7个失效数据为定数截尾数据，r2=7，且有t21=505,t22=526,…,t27=789。

对子样t11≤t12≤…≤t1r1和t21≤t22≤…≤t2r2作变换，即xi=lnt1i，yi=lnt2i。

对第1组子样：n1=16，r1=12，查最好线性无偏估计表并查最好线性无偏估计表，经计算得

第2组子样：n2=12，r2=7，查最好线性无偏估计表，经计算得分别计算得

接受原假设H0，即m1=m2。可认为2单位的发动机主机失效机理相同，失效机理一致性假设成立。

2.3 环境因子计算

解决数据间相互折算问题的关键是确定不同环境下环境因子的值。利用这一数值可以把某环境下的寿命数据等效折算为另一环境下的寿命数据。2种环境下，若产品的失效机理相同，即m1=m2=m 时，文献[9]定义的威布尔分布环境因子

由m1=m2可知m2=5.589。

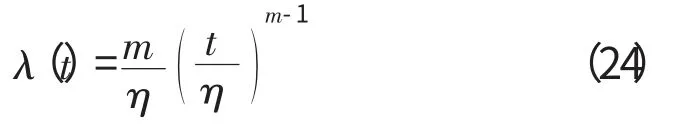
由式（24）可得η2=837.902。

由式（23）可得

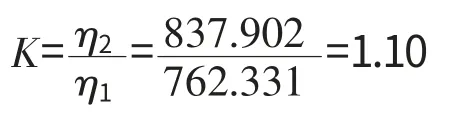
综上，由于单位1的环境条件比单位2的恶劣，且发动机主机在此环境中的使用寿命缩短，其使用可靠性比单位2的低。说明高温高盐高湿的沿海环境对发动机的使用可靠性影响很大。

3 主机故障特点分析及故障防护

3.1 主机故障特点

主机故障数据如图2所示。

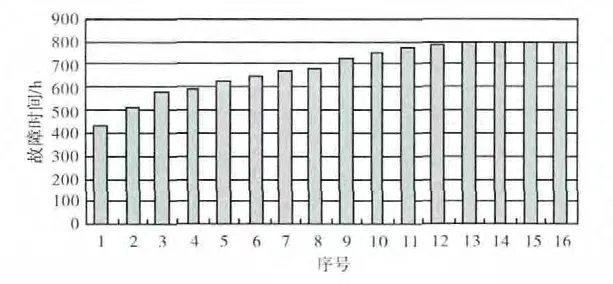
图2 主机故障数据

从图2中可见，主机有明显的耗损失效期，在工作600h以后故障率随时间增加逐渐升高，且上升趋势较快。这种失效由耗损或老化引起，因此在总寿命期间的工作初期较少出现。

主机故障表现得形式广、类型多、造成的后果也较严重。其形式大体上有强度不足造成破裂与损伤、高周疲劳损伤、低周疲劳损伤、热疲劳损伤、高振动应力下的累积疲劳损伤、蠕变与破裂、交互作用损伤等结构强度型故障，约占发动机总故障的20%，其中又以各类机件磨损为主，各类疲劳损伤故障为辅。

航空发动机在使用过程中，大量部件由于高速旋转，易发生因运转部件磨损而引起的故障，如自由涡轮前后轴承、主动齿轮前后轴承和轴承保持架、外置机匣轴承、轴间轴承、封严圈、轴承轴套的严重磨损等[10]。这些磨损故障不但影响发动机在正常寿命期的使用，而且限制了发动机的延长使用。

随着能量与质量的变化，发动机主机零部件会发生磨损、腐蚀、疲劳、老化等，其过程不可逆。表现为发动机老化程度逐步加剧，故障逐渐增多。随着使用时间的增加，局部故障的排除虽能恢复整机的部分性能，但整机故障率仍不断提高，新的故障不断出现。同时其损伤也不能完全消除，即使维修也不可能使发动机整机的性能恢复到使用前状态。

3.2 主机故障防护建议

3.2.1 对使用单位的建议

为减少发动机主机故障的发生，建议使用单位从以下几方面采取以下措施：

（1）在飞机海上飞行后或发动机在使用一段时间后对发动机进行冲洗，清洁掉积存在机件表面的盐垢等，避免发动机被腐蚀。

（2）加强对发动机滑油的监控，预报磨损和失效状况，便于采取预防性维修措施，确保发动机的可靠使用和高效发挥应有功能。

3.2.2 对生产单位的建议

为减少故障发生，建议生产单位从设计和加工质量等环节上采取措施，从根源上解决避免故障的发生问题。这就要求生产方单位严格贯彻可靠性设计规范，保证产品在寿命期的可靠性。建议开展以下工作：

（1）进行发动机在海洋环境下防腐能力试验。湿热环境容易引起发动机金属材料的氧化和腐蚀。而腐蚀是影响发动机可靠性的主要问题，应加强对发动机成附件腐蚀防护与控制能力的研究。

（2）改进零部件。根据关键零组件的强度核实和寿命确定工作的实际情况，进行发动机某些零部件的改进。

（3）开展发动机整机的抗腐蚀性试验研究。

4 结束语

本文在搜集某单位发动机主机使用数据并对数据进行分布拟合检验的基础上，分析了发动机主机的使用可靠性。结合另一单位同型发动机的寿命数据对其可靠性环境因子进行研究。在失效机理相同的情况下，确定沿海高盐高湿的环境对主机寿命影响较大。对主机的故障特点进行分析，分别从使用单位和生产单位2种角度提出了提高发动机使用可靠性的对策。研究结果可为航空发动机的研制生产和使用维护提供一定的指导。

航空发动机可靠性环境因子涉及问题较多，研究工作量大，受条件和数据限制，本文仅对其中部分问题进行了研究，而发动机附件是否受海洋环境影响，发动机轴承磨损及发动机经翻修后的使用可靠性等问题，都值得进一步研究。

[1]赵宇.可靠性数据分析[M].北京：国防工业出版社，2011：36-45.ZHAO Yu.Reliability data analysis[M].Bei Jing：Defense Industry Press，2011：36-45.（in Chinese）

[2]游达章.最小二乘法在威布尔分布的可靠性评估[J].湖北工业大学学报，2009（4）：27-29.YOU Dazhang.Reliability assessment of the least squares method in the Weibull distribution[J].Journal of Hubei University of Technology，2009（4）：27-29.（in Chinese）

[3]王炳兴.Weibull分布环境因子的统计分析[J].系统工程与电子技术，2002（24）：126-128.WANG Bingxing.Statistical analysis of the Weibull distribution environmental factor[J].Systems Engineering and Electronics，2002（24）：126-128.（in Chinese）

[4]赵婉，温玉全.可靠性评估领域中环境因子的研究进展[J].电子产品可靠性与环境试验，2005（2）：69-72.ZHAO Wan，WEN Yuquan.The resaarch status of environmental factor in reliability assessment[J].Electronic Product Reliability and Environmental Testing，2005（2）：69-72.（in Chinese）

[5]盖京波，王善.威布尔分布的环境因子[J].安全与环境学报，2002，2（3）：58-60.GAI Jingbo，WANG Shan.Environmental factor of Weibull distribution[J].Journal of Safety and Environment，2002，2（3）：58-60.（in Chinese）

[6]李凤.环境因子估计理论及其在可靠性评估中的应用[D].西安：西北工业大学，2007.LI Feng.Environmental factor esimation theory and it’s utilization in reliability assessment[D].Xian：Northwestern Polytechnical University，2007.（in Chinese）

[7]徐锦龙，费鹤良.多个威布尔形状参数的检验[J].上海师范学院学报，1984（3）：27-32.XU Jinlong，FEI Heliang.The test of multiple Weibull shape parameter[J].Journal of Shanghai Normal University，1984（3）：27-32.（in Chinese）

[8]孙艳君，宋立新.定数截尾下Weibull分布形状参数的假设检验[J].衡水学院学报，2010，12（1）：12-13.SUN Yanjun，SONG Lixin.Hypothesis test of shape parameter in Weibull distribution under censored[J].Journal of Hengshui College，2010，12（1）：12-13.（in Chinese）

[9]贾占强，蔡金燕，梁玉英.产品性能可靠性评估中的环境因子仿真研究[J].红外与毫米波学报，2010，29（3）：172-175.JIA Zhanqiang，CAI Jinyan，LANG Yuying.Simulation study of environmental factors in the evaluation of product performance reliability[J].Journal of Infrared and Millimeter Waves，2010，29（3）：172-175.（in Chinese）

[10]陈立波，宋兰琪，陈果.航空发动机滑油综合监控中的磨损故障[J].航空动力学报，2009，24（1）：169-175.CHEN Libo，SONG Lanqi，CHEN Guo.Wear failure of aeroengine oil comprehensive monitoring[J].Journal of Aerospace Power，2009，24（1）：169-175.（in Chinese）

[11]金如山.航空燃气轮机燃烧室[M].北京：宇航出版社，1988：7-8.JIN Rushan.Gas turbine combustor[M].Beijing：China Astronautic Press，1988：7-8.（in Chinese）

[12]何琳楠，刘振兴.航空发动机实验数据库的构建[J].燃气涡轮试验与研究，2010，23（4）：57-60.HE Linnan，LIU Zhenxing.Construction of aeroengine test database[J].Gas Turbine Experiment and Research，2010，23（4）：57-60.（in Chinese）

[13]唐耿林.航空发动机性能监视参数选择的研究[J].推进技术，1988，19（2）：18-19.TANG Genglin.Aeroengine performance parameter chosen approach[J].Journal of Propulsion Technology，1988，19（2）：18-19.（in Chinese）

[14]郑波，朱新宇.航空发动机故障诊断技术研究[J].航空发动机，2010，36（2）：22-25.ZHENG Bo,ZHU Xinyu.Aeroengine malfunction diagnosis[J].Aeroengine，2010，36（2）：22-25.（in Chinese）

[15]张传超，史永胜.航空发动机健康管理技术进展及趋势[J].航空发动机，2008，34（4）：51-53.ZHANG Chuanchao，SHI Yongsheng.Aeroengine health management development[J].Aeroengine，2008，34（4）：51-53.（in Chinese）