圆筒框架稳定分析

严 峰

(中石化上海工程有限公司，上海 200120)

1 工程简介

某海外项目4 000 m3料仓钢支承结构，结构形式为空心圆筒式框架，框架沿径向没有任何梁的约束，仅沿圆切线方向布置了封闭柱间支撑，如图1 所示。常规的钢结构稳定分析首先需要根据框架两个主轴方向是否设置了柱间支撑，柱间支撑的刚度是否满足强支撑要求来区分其属于有侧移失稳还是无侧移失稳，进而确定不同的计算长度系数开展后续分析。这类圆筒框架难以简单区分侧移情况，需要综合计入各种构件相互之间约束影响，按结构稳定理论的方法来进行相关设计。本文从多方法对此类框架的整体稳定性做了细致的研究。

图1 料仓框架计算简图及Load Cell 照片

料仓框架主要由三部分组成，最顶部为钢结构平台和相关风送系统管线及其支架，顶平台主要支承在料仓筒壁上(图中未显示)。中间层为料仓本体，底层为高度17 m 的钢结构圆筒形框架。本结构特殊之处还在于料仓材质为铝材，设备刚度偏弱且主要通过称重模块(Load Cell)支承在柱顶环梁上，称重模块与环梁采取了限位装置防止其大位移滑移除此之外没有其他强连接。这种连接构造只允许料仓向结构传递竖向压力和水平地震或风荷载，无法形成对下部钢结构的任何侧向刚度约束贡献。每台料仓框架共设置8 根框架柱均匀分布在直径约14 m 的圆周上，框架柱采用焊接双H 十字形截面，沿结构环向设置连续的柱间支撑，框架径向由于料仓系统出料的要求不得设置任何构件，整体形成了空心圆筒形式。

2 规范方法

在现行的设计方法中，对于钢框架结构的稳定分析主要使用的是传统计算长度法(Effective Length Method)。根据美国国际标准建筑规范ANSI/AISC 360—2005 LRFD［1］(以下简称AISC 360)规定若采用计算长度系数法须考虑在每层柱顶施加假想水平力(Additive motional lateral load)来考虑结构整体初始几何缺陷的影响。AISC 360 规范给出了纯弯框架、带支撑或者剪力墙的框架情况下的计算长度的取值方法，能够处理多数简单边界条件下的杆件计算长度。对于本文这类边界条件较为复杂的杆件或者非常规的框架，规范给出确定的无侧移框架的判别准则为二阶位移与一阶位移比值:

表1 列出了两种工况下节点一阶和二阶弹性位移比值，弹性分析时框架位移表现出与常规框架不同的特点。通常情况在竖向和水平荷载作用下框架柱顶位移一般最大，而该料仓框架的各节点侧移变形呈现顶层底层大中间层最小，而二阶与一阶位移比值却是中间比两头大，同类型结构不能仅依据框架柱顶位移比值做简单判断。弹性侧移分布情况与之字形柱间支撑设置有着密切的关系，框架出现整体绕圆筒切线扭转的趋势。验算结果表明无论正常操作工况还是最大试压荷载下框架中间节点位移比值处于1.10 限值附近，计算长度系数还需要进一步研究确定。

表1 框架二阶与一阶弹性位移

3 压杆屈曲分析

料仓框架结构形式比较规整，可以通过进行合理的假定和简化构件的边界条件，根据力学的理论建立微分方程进行求解。计算表明框架柱顶径向无侧移时柱间支撑的最小截面面积要求为23 cm2，通常情况下设置了型钢截面的柱间支撑都满足柱顶无侧移刚度的要求，因而柱顶可以判定为框架的不动铰支座，框架可以进一步简化为多个弹性支承上的轴心受压构件。

文献［2］给出了弹性支座压杆临界力P 与弹性支座刚度K 的相关性公式如式(1)，其中，P0为中间两道支撑均为刚性支座时的压杆临界力;L 为压杆长度。式(3)的力学含义为屈曲半波长等于柱间弹性支座的间距，即框架各层均为无侧移失稳模态。

取环向典型榀柱间支撑忽略环向撑杆刚度影响，合并整理并考虑柱间环向支撑与框架柱径向主轴夹角φ=22.5°可以求得二层径向折算刚度如式(4)。

其中，E 为钢材弹性模量;Ab和Ac分别为环梁和框架柱截面面积;φ 为柱间支撑夹角;h 为节间高度。

二层径向刚度:

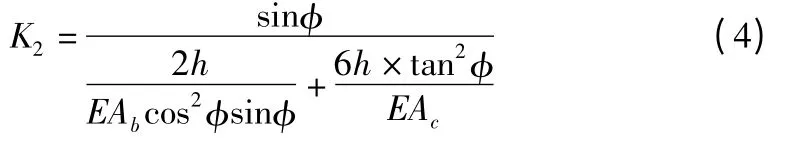
计算长度系数:

根据文献［3］相关研究，在考虑构件初始屈曲和安装缺陷要求时，支撑的刚度需要较无缺陷杆件求得的刚度放大2 倍～3 倍。试算表明无论设置多么强大的柱间支撑，其刚度K 均无法满足式(3)要求，即无法满足柱中无侧移要求。取缺陷折减后的刚度代入联合求解式(4)和式(5)，可以求得本框架计算长度系数μ 约为0.45。

4 特征值屈曲分析方法

特征值屈曲分析即结构弹性稳定分析(Buckling)，指结构在外荷载作用下，在原来的平衡状态之外出现结构的分叉点，使用特征值的公式计算造成结构负刚度的应力刚度矩阵的比例因子。特征值屈曲分析的优点是计算快。在进行非线性屈曲分析之前我们可以利用线性屈曲分析了解屈曲形状，并可以用于确定柱的计算长度系数［4，5］。屈曲分析宏观上代表了结构失稳的趋势，与规范规定的方法、物理意义完全不同。由于特征值屈曲不考虑任何非线性和初始缺陷，因此它只是一种理想状态的解，利用特征值屈曲分析可以预测出屈曲载荷的上限。

采用恒载与活载的荷载组合，求得的前三阶屈曲模态如图2 所示，图中左侧为三维视图，右侧为俯视图。各阶屈曲模态主要表现为平面没有刚性楼板约束产生沿径向的变形，该结果与直观的判断径向偏弱基本一致，没有表现出整层侧移屈曲形态。模态2 和模态3 屈曲特征值完全相同仅表现为模态旋转了90°。

图2 屈曲模态

表2 列出了前四阶屈曲的荷载因子和框架柱计算长度系数情况，通常情况第一阶屈曲模态对应的计算长度最为不利，因此该框架柱计算长度为9.8 m。

表2 柱计算长度系数

5 精确分析方法

为进一步考查结构的受力性能，对上述框架整体进行了二阶非线性弹塑性有限元分析，框架柱截面残余应力分布情况参考了欧洲钢结构协会［6］(ECCS)推荐的方案并考虑了焊接十字H 截面腹板部位的焊接应力集中特殊性，见图3。框架柱顶点侧倾缺陷按计，缺陷方位参照特征值屈曲分析模态1。其中，m 为柱列数量。该系数是考虑实际框架中不同柱子的初始缺陷方向可能是不同，产生的不利影响会相互抵消，因此引入作为统计折减系数。另行叠加杆件初始弯曲缺陷，其中，l0为框架柱的层高或者是支撑构件的轴线长度。图4 为轴力与变形关系曲线，圆点实线为有限元分析结果，两条虚线分别表示采用折减刚度求得计算长度和屈曲分析得到的计算长度对应的极限承载力。分析结果表明折减刚度得到的极限承载力与有限元分析结果能够较好吻合，屈曲分析的结果差异稍大。

图3 残余应力分布

图4 轴力与变形曲线

6 结语

AISC 360 规范给出根据二阶弹性位移和一阶弹性分析位移比值小于1.1 时可以按无侧移框架求解，该假设要求是有适用条件的。对于本文所示的剪切形圆筒型框架，需要核查每个柱间节点的位移比值，以免造成误判。

计算表明只要设置很小截面柱间支撑即可满足框架柱顶无侧移的刚度要求，但对于框架中间部位即使设置封闭的柱间支撑依然无法满足层间无侧移刚度要求，因此在设计时应注意验算柱间支撑的刚度要求。基于折减刚度求得极限承载力与二阶弹塑性有限元精确分析吻合程度较高，相关公式满足工程实用精度需求。

［1］AISC 360，Specification for Structural Steel Building［S］.

［2］陈绍蕃.具有多道弹性支撑杆的钢柱稳定计算［J］.西安建筑科技大学学报(自然科学版)，2011，43(2):153-159.

［3］童根树.钢结构平面内稳定［M］.北京:中国建筑工业出版社，2005.

［4］童根树，饶芝英.一个奇特的除尘器钢支架的屈曲问题［J］.建筑钢结构进展，2007，9(5):42-46.

［5］顾 建.特殊框架柱计算长度的确定［J］.建筑结构，2011，41(sup):926-928.

［6］ENV 1993-1-1，Eurocode 3:Design of Steel Structure Part1.1:General rules for Buildings［S］.