考虑高阶振型阻尼比的结构响应研究

梁晓东 李双龙 汪忠明 王传甲

(1.奥意建筑工程设计有限公司，广东 深圳 518031;2.合肥工业大学土木与水利工程学院，安徽 合肥 230009)

0 引言

阻尼是用来描述结构在振动过程中能量耗散特征的参数，是影响结构动力反应的重要因素之一。在地震反应时程中，有足够的阻尼存在，结构就能吸收较多的地震动能量，可以有效地减小振幅和应力，改善结构的振动状况。基于对阻尼的认识，国内外学者们提出了不同的阻尼模型［1-5］，并对阻尼模型进行了一些分析研究与扩展［6，7］。这类阻尼模型基本上可以分为两类，一类基于阻尼的物理过程描述，每种假设对应着一种具体的阻尼现象;一类着重数学处理上的方便，并不跟某种具体的阻尼物理过程相对应。鉴于结构在地震反应分析中阻尼机理的复杂性，没有哪种阻尼理论能涵盖和解释结构动力分析中阻尼耗能的所有物理过程。人们对结构地震反应分析主要是为了获知结构反应量，因此在工程分析中常选取数学处理上比较方便的阻尼模型，根据与结构反应物理量等效的原则来确定阻尼参数。

在建筑结构的动力分析中，出于使用方便，人们常使用正交阻尼，而非正交阻尼因为计算较为麻烦用得较少。最一般的正交阻尼矩阵是Caughey 阻尼矩阵［4］，Caughey 阻尼在满足与振型正交的同时，可以指定系统的j 个(j=1～n)振型的阻尼比，其中n 为体系的自由度。当r=2，即指定两个振型的阻尼比时，就是Rayleigh 阻尼。尽管Caughey 经典阻尼矩阵使得指定任意阶振型的阻尼系数成为可能，但是Caughey 阻尼在数值上是具有病态条件的，因为系数可能会相差几个数量级，而且，如果在Caughey级数中包含两项以上时，尽管k 是带状矩阵，对于集中质量体系，m是对角矩阵，但c 将是满阵，这样会极大地增加大型体系分析的计算代价。而Rayleigh 阻尼模型虽然实施起来方便，但是本身也有很多缺陷:首先，从物理上讲，刚度比例阻尼部分βK 从直觉上很容易接受，因为它可以用来模拟层间变形所产生的能量耗散，但是质量比例阻尼αM 则很难理解，因为用它来模拟的空气阻尼在大多数结构中很小，可以忽略不计。

其次，在考虑的结构反应中，一般取较低的两阶频率和阻尼比来确定阻尼常数α 和β，用这种方法确定的阻尼常数，只能保证两个振型的阻尼比为一个指定经验值，难以保证其他振型的阻尼比也为同一个值。当用以上方法得出的计算阻尼比小于指定值时，则计算结果对振型阻尼估计不足，计算效应偏大，可能导致设计偏保守;相反，当用此法得出的计算阻尼比大于指定值时，则计算结果对振型阻尼估计过大，计算效应偏小，可能导致设计偏不安全。

最后，在通常的大型动力时程计算中，由于刚度退化引起的数值不收敛，因此常采用仅设α 系数的策略来算Rayleigh 阻尼，这样实际上不仅物理上解释不通，而且得出来的值，会使设计偏保守，提高成本。

目前，公认可靠的结论是上部结构体系具有在相当宽的频率范围内模态阻尼比不变的特性，而且偏于保守的，结构的下部阻尼不予考虑，我国规范规定，一般混凝土结构为0.05。

随着基于性能的抗震设计方法的提出，对结构在罕遇地震作用下的弹塑性时程分析的清楚把握必不可少，而ABAQUS 以其强健的非线性计算能力、广泛的模拟性能和多种灵活的接口，在科学研究和工程领域得到了广泛的开发应用。

本文通过振型向量构造适当的阻尼矩阵，使结构多阶振型的阻尼比可以为指定值，对ABAQUS 进行二次开发，利用编制的子程序将等效阻尼力正确地施加在结构上，并计算比较了一工程结构考虑多阶振型阻尼比的层间位移角和基底剪力结果。

1 阻尼矩阵构造

当包括阻尼时，结构的动力学方程［8］为:

式中:u——节点位移矢量;

m——质量矩阵;

c——阻尼矩阵;

k——刚度矩阵;

p(t)——随时间变化的外力矢量函数。

将节点位移矢量u 以固有振型为基展开:

式中:qr——振型坐标;

φr——第r 阶振型矢量;

Φ——N×N 阶振型矩阵。

将式(2)代入式(1)，并且前乘ΦT，得到:

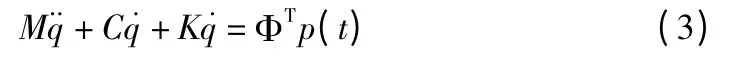
其中，M=ΦTmΦ;C=ΦTcΦ;K=ΦTkΦ，固有振型的正交性意味着M，K 是对角阵，如果要使式(3)解耦，则C 必须也是对角阵，即:

其中，diag()为对角阵函数。

式(3)的分量形式为:

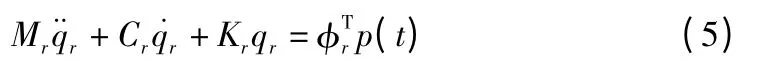
式(5)变形为:

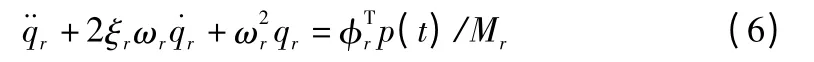
其中，ξr为第r 阶振型的阻尼比，ξr=cr/2ωrMr。

利用M=ΦTmΦ，式(4)变为:

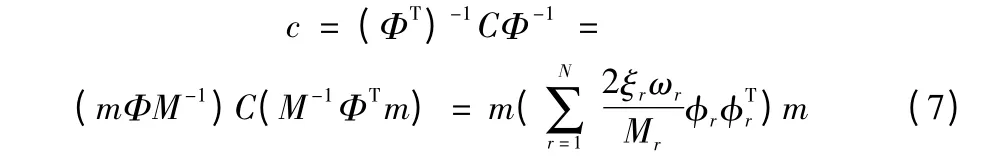
这样构造出的阻尼矩阵c［8］不仅使得式(3)能解耦为分量形式的式(5)，而且能够使相当宽的频率范围内结构的振型阻尼比为指定值，考虑到计算效率，式(6)中只包括前J 个振型是合理的，因为这些振型对于反应的贡献是主要的。因此，式(7)改写为:

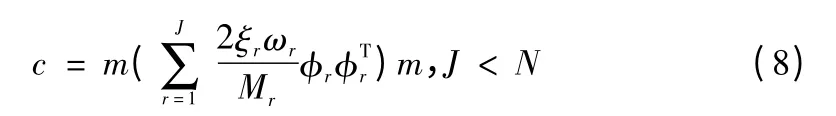
根据以上公式编制程序实现阻尼矩阵的多阶振型表达。

2 工程算例分析和ABAQUS 二次开发实现

2.1 工程概况

合肥置地广场·A 座项目位于安徽省合肥市城市新中心——政务文化新区，北依龙图路，东临星光西路，西靠怀宁路。项目用地北面为省广电中心，东面为城市绿轴景观带，西面为省文博园。项目总占地面积51 188 m2，总建筑面积达到380 000 m2，结构三维模型如图1 所示。

图1 三维结构模型图

本工程地上47 层，地下4 层，主要屋面标高为197.60 m，采用钢筋混凝土框架—核心筒结构体系。计算嵌固端取为地下室顶板面，一层楼面在主塔楼周边设置抗震缝。为减小柱截面，在结构的中下部采用型钢混凝土柱，上部采用普通混凝土柱。框架梁采用钢筋混凝土梁。

2.2 计算模型与相关参数选取

本场地特征周期为0.37 s，弹性动力时程分析时，时长为40 s，步长为0.01 s，地震加速度最大值为344.49 cm/s2。

取地下室顶板以上结构为弹性动力时程分析对象，地震波从地下室2 层顶板处的竖向构件端点输入，结构分析模型由弹性梁单元与弹性壳单元构成。梁与柱采用可考虑线性剪切变形效应的Timoshenko 梁单元B31，墙、楼板及连梁采用4 节点缩减积分壳单元S4R 和S3。

2.3 ABAQUS 二次开发

本文基于大型通用有限元软件ABAQUS/Explicit 求解器［9］，开发VDLOAD 子程序将构造的阻尼矩阵通过阻尼力的形式施加在工程结构上，代替了原有的低阶阻尼模块，对一工程结构在振型累积质量参与系数超过90% 的阶数下，进行弹性动力时程分析。

在ABAQUS 中，VDLOAD 子程序被用来给一个或多个点集定义随位置、时间、速度等变化的分布力，这些点出现在基于单元或表面的非均匀载荷定义里，VDLOAD 子程序在积分点处被调用。VDLOAD 子程序里的变量说明如下:

value:分布力的大小;nblock:调用点的数目;ndim:坐标方向数目。

steptime:时间步长;totaltime:总时间;curCoords:调用点的当前坐标。

amplitude:引用荷载幅值的当前值;velocity:调用点的当前速度。

dirCos:压力类型荷载下，表面、边、管或梁的方向余弦。

jltype:分布力类型标识符。

通过VDLOAD 将阻尼矩阵变为阻尼力施加于结构，并指定各阶振型下阻尼比都为0.05。

2.4 层间位移角和基底剪力分析结果比较

将构造的阻尼矩阵退化为只使用一阶振型向量来考虑阻尼，用本文开发的子程序与ABAQUS 自带的α 阻尼下的层间位移角和基底剪力进行了比较，结果如图2 和图3 所示，吻合程度很高，验证了构造的阻尼矩阵的合理性。当仅考虑一阶振型α 阻尼比时，本文比较了指定多阶振型阻尼比情况下的层间位移角和基底剪力，进而使用此程序计算多阶振型下的响应，由图4 和图5 可以看出，考虑不同阶振型下的结构层间位移角，随着计入振型数的增多，层间位移角逐渐变小，类似地，基底剪力随着振型数的增多，剪力幅值也逐渐减小，说明考虑的振型数越多，阻尼消耗的能量越多，同时当振型数取到一定值时，后面的贡献变得很小。这样对于超高层结构，比只考虑两阶振型的Rayleigh 阻尼或仅考虑一阶振型的α 阻尼更能准确地反映真实结构的耗能及基底剪力态势，为结构设计提供指导。

图2 层间位移角结果比较

图3 基底剪力结果比较

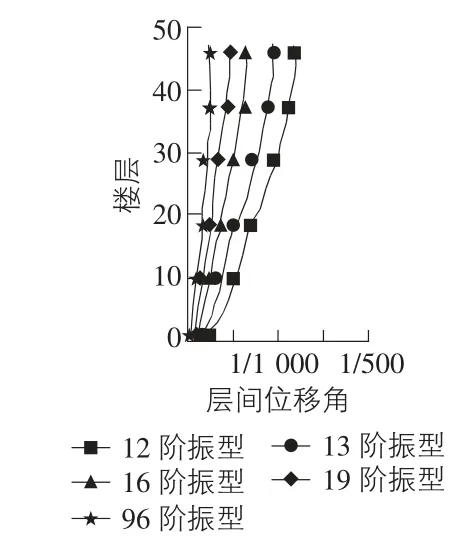
图4 Y 向层间位移角比较

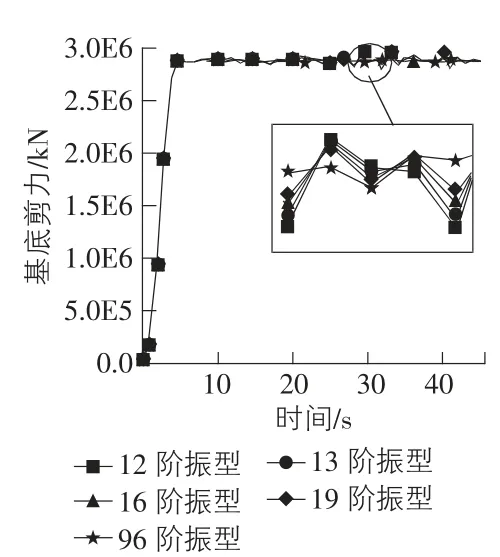
图5 Y 向基底剪力比较

3 结语

通过基于ABAQUS 二次开发平台施加的多阶振型阻尼力的动力时程分析计算，可以得出:高振型阻尼比主要影响结构的层间位移角和基底剪力，特别是结构的中上部的层间位移角，若采用不计高振型阻尼比影响的Rayleigh 阻尼，结构在地震作用下的层间位移角偏大，不能反映结构真实高阶振型的影响，基于此分析结果的设计控制会相对偏于保守，而通过施加高阶振型阻尼比的分析，更加能客观地反映超高层结构的高阶响应，基于此设计控制能合理地降低成本，为设计提供理论依据。

［1］Bert，C W.Material Damping:An Introductory Review of Mathematical Models，Measures and Experimental Techniques［J］.Journal of Sound and Vibration，1973，29(2):129-153.

［2］Leger P，Dussault S.Seismic-Energy Dissipation in MDOF Structures［J］.Journal of Structural Engineering，1992，118(5):1251-1269.

［3］Hart，G C，Vasudevan R.Earthquake Design of Buildings:Damping［J］.Journal of the Structural Division，ASCE，1975，101(1):11-30.

［4］Clough R W，Penzien J.Dynamics of Structures ［M］.New York:McGraw-Hill，1975.

［5］Liang Z，Lee G C.Representation of Damping Matrix ［J］.Journal of Engineering Mechanics，ASCE，1991，117(5):1005-1019.

［6］黄宗明，白绍良，赖 明.结构地震反应时程分析中的阻尼问题评述［J］.地震工程与工程振动，1996，16(2):95-104.

［7］董 军，邓洪洲，王肇民.结构动力分析阻尼模型研究［J］.世界地震工程，2000，16(4):63-69.

［8］A K Chopra.结构动力学:理论及其在地震工程中的应用［M］.第2 版.谢礼立，吕大刚，译.北京:高等教育出版社，2007.

［9］ABAQUS Inc.ABAQUS User's Manual，V6-9，2009.