基于周期-摆幅测量的摆式陀螺全方位快速预定向方法
陈河,张志利,周召发,赵晓枫
(第二炮兵工程大学,陕西西安710025)
基于周期-摆幅测量的摆式陀螺全方位快速预定向方法
陈河,张志利,周召发,赵晓枫
(第二炮兵工程大学,陕西西安710025)
为克服目前国内摆式陀螺寻北仪难以实现全方位寻北的不足,通过对其大偏北角运动规律的分析提出了一种基于周期-摆幅测量的全方位快速预定向方法,通过测量摆动周期和摆幅计算偏北角;分析了转子转速对预定向时间的影响,以及各参数误差对预定向精度的影响,并对提出的方法进行了初步试验验证。理论分析和试验结果均表明,通过降低转子转速可以有效缩短摆动周期,在65 s内实现全方位预定向,精度在5°以内,满足后续寻北过程的精度要求。
兵器科学与技术;摆式陀螺寻北仪;大偏北角;全方位寻北;周期-摆幅测量
0 引言
陀螺寻北技术自主性强,精度高,不依赖外界信息,可全天候使用,在军事和民用领域得到了广泛应用。其中,捷联式陀螺寻北仪寻北时间3~5 min,精度1′~3′,主要应用于对寻北速度要求较高而精度要求不高的场合[1];而摆式陀螺寻北仪寻北时间一般在10 min左右,精度可达5″以内,广泛应用于对寻北精度要求较高的场合,如大地测量、矿山测量、科学实验等民用测量领域,以及火炮、导弹、航空航天等军事测量中[2]。国外以德国Gyromat-2000为代表的先进摆式陀螺寻北仪能实现任意初始架设方位全自动快速高精度寻北[2]。国产同类仪器虽然已经实现自动化,寻北精度也与国外仪器相当,但对初始架设方位要求严格,需要采用磁罗盘概略定北;磁罗盘定向易受环境磁场影响,难以保证可靠性[3]。为了克服上述问题,文献[4]提出利用检测陀螺力矩进行全方位预定向,能够实现-90°~90°任意方位粗寻北,但还不能实现全方位(-180°~180°)寻北,且微小力矩量的检测也比较困难;文献[5]将步进迭代法应用于全方位预定向,并对步进策略进行了优化,但该方法中对步进时机的判断比较困难。
摆式陀螺运动规律是寻北方法研究的基础。由于大偏北角情况下陀螺运动方程为非线性微分方程,研究起来比较复杂,目前对其大偏北角运动规律的理论和试验研究都很少[6]。只有文献[6]运用李雅普诺夫稳定性理论分析了其寻北稳定性,文献[7]对其大偏北角运动规律进行了数值仿真,文献[5]用正弦曲线对运动方程的数值解进行了拟合。上述文献对摆式陀螺的全局运动规律进行了分析,但未得到方程的解析解或近似解析解,不利于分析运动规律随结构参数的变化规律。相应地,对寻北方法的研究也大都以小偏北角运动规律为基础,研究真北附近的快速粗寻北和精寻北[8-10],而缺乏对其任意初始架设方位下的全方位快速预定向方法的研究。
本文首先利用欧拉动力学方程建立摆式陀螺大偏北角运动方程,然后根据相平面法分析其全局运动规律,运用牛顿-谐波平衡法求得周期摆动的近似解析解;根据得到的解析解提出采用周期-摆幅测量法实现全方位快速预定向,并对其效果进行了详细讨论。
1 摆式陀螺大偏北角运动规律
1.1 摆式陀螺运动方程
如图1所示,陀螺灵敏部由陀螺房、陀螺转子和悬挂柱组成,它通过悬挂带悬挂于仪器的壳体上,处于自由悬挂状态。悬挂带长为l,灵敏部重心为G,悬挂带与陀螺房接触点为O1,G与O1的距离为a,与转子中心O2距离为d.寻北时转子轴偏离真北的水平角为α(逆时针为正,-180°~180°),俯仰角为β(逆时针为正,0°~90°),悬挂带与铅垂线夹角为γ,寻北点的纬度为φ.
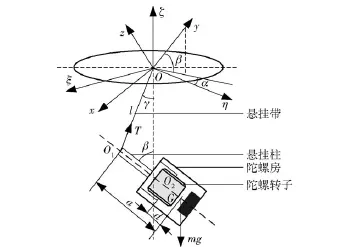
图1 陀螺灵敏部力学模型Fig.1 Mechanical model of pendulous gyroscope
图1中坐标系Oξηζ(OENZ)为固连于地球的地理坐标系,Oξ(OE)指向东,Oη(ON)指向真北,Oζ(OZ)指向天顶;坐标系Oxyz,原点为O,z轴沿陀螺房对称轴指向上,y轴与转子自转角动量方向一致,x按右手法则确定。根据欧拉动力学方程,忽略次要因素,可得陀螺灵敏部运动方程[5-7]如下:
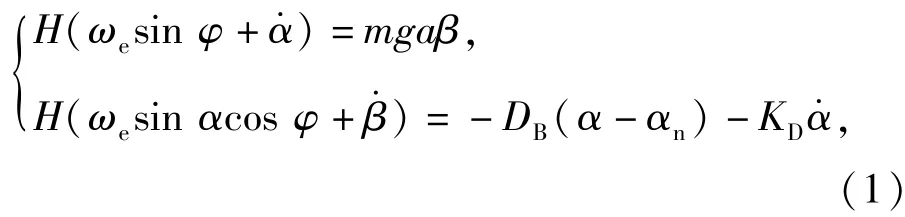
式中:H为转子自转角动量;ωe为地球自转角速度;m为灵敏部质量;g为重力加速度;αn为悬挂带扭矩为零时的方位角;DB为悬挂带扭力系数;KD为阻尼系数。
该方程为平面自治系统。由于空气阻尼很小,忽略KD
[7].将方程(1)式中一式的β代入二式,令DK=Hωecosφ,K=DB/DK,得α满足方程
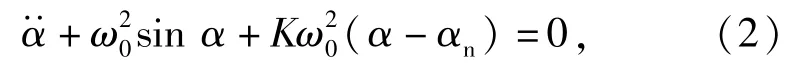
β满足方程
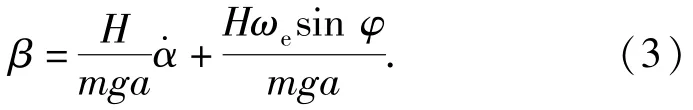
由(2)式求得α,代入(3)式可求得β.偏北角α较小时,(2)式可近似为线性方程,这是目前研究的比较多的一种情况;而α较大时,方程为非线性方程,目前研究的比较少。
1.2 相平面分析及全局运动规律
由(2)式知α的平衡位置α*满足
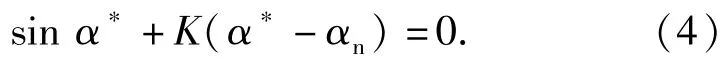
由(4)式可知偏北角α的平衡位置α*的个数和数值取决于K和αn,且没有一般的解析解。如图2所示,α*为y=sinx与y=-K(x-αn)的交点。当0<K<1时,平衡位置的个数不仅与K有关,还与αn有关,情况比较复杂;当K≥1时,只有一个平衡位置。
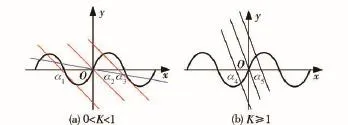
图2 偏北角平衡位置情况示意图Fig.2 Equilibrium positions of α with different K
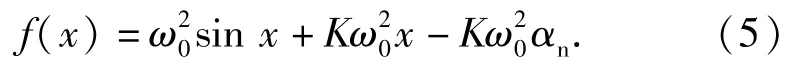
势能函数为
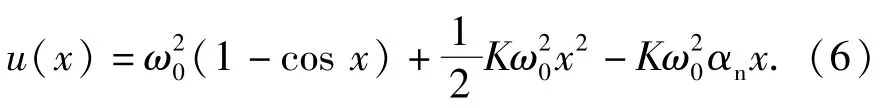
1)若K≥1,对(5)式中恢复力函数有
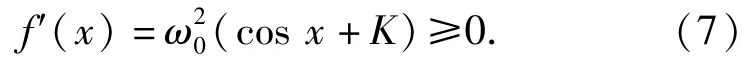
由(7)式可知恢复力函数单调递增,且f(α*)= 0,则x<α*时,f(x)<0;x>α*时,f(x)>0.于是x<α*时,u(x)单调递减;x>α*时,u(x)单调递增。α*为u(x)唯一极小值点,则可得势能函数及相轨迹如图3(a)所示,可见灵敏部绕其平衡点作周期性摆动。由于u(x)关于x=α*不对称,灵敏部在平衡点左右的摆动并不对称。值得注意的是,在这种情况下,平衡位置不一定在真北附近,如对某陀螺样机,m=2.0 kg,g=9.8 m/s2,a=0.12 m,H= 0.19 kg·m2/s,ωe=7.29×10-5rad/s,φ=34°,K= 2.67.当αn=2π/3 rad时,唯一平衡点为α*= 1.724 3 rad,不再位于真北附近。特别地,当αn= 0 rad时,α*=0 rad,稳定平衡位置在真北方向;当αn=π rad时,α*=π rad,稳定平衡位置在正南方向。
2)若0<K<1,需要进行具体分析。具体思路是,根据恢复力函数曲线判断平衡点的个数并求出相应的平衡点,然后根据相平面法得到平衡点的稳定性及全局运动规律。例如,αn=2π/3 rad,K=0.6时,系统仅有一个平衡点α*=0.846 3 rad,且f′(0.846 3)=0.001,α*为势能函数的极小值点,相轨迹如图3(b)所示,可以看出该平衡点为稳定平衡点;当αn=2π/3 rad,K=0.3时,系统有3个平衡点,分别为α*=0.499 1 rad,3.615 4 rad,5.134 8 rad,对应的f′(α*)分别为0.000 88,-0.000 44,0.000 53,所以0.499 1 rad和5.134 8 rad为势能函数的极小值点,是稳定平衡点,3.615 4 rad为势能函数极大值点,不稳定,其相轨迹如图3(c)所示。在实际寻北时,α在[-π rad,π rad)范围内,且初速度很小,扭力零位与初始位置很接近,系统的初始状态在平衡点0.499 1附近,所以灵敏部实际上会在平衡点0.499 1附近摆动。
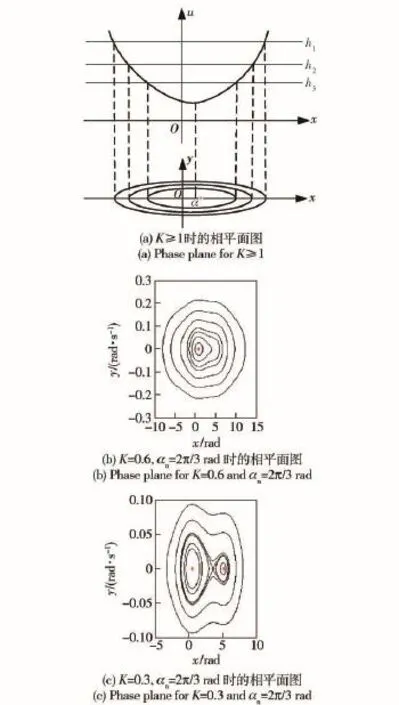
图3 不同条件下偏北角变化的相轨迹Fig.3 Phase trajectories of α in different conditions
从图2可知,即使在0<K<1的情况下,系统也必有一个平衡点在区间[-π rad,π rad)内。对于α*∈(-π rad,π rad),有f′(α*)>0,所以其为极小值点,平衡点稳定;对于α*=-π rad,f′(α*)=0,其左右邻域的点均满足f′(α*)>0,所以它也是极小值点,为稳定平衡点,即正南方向也有可能是稳定平衡点。实际寻北时,陀螺灵敏部应作绕[-π rad,π rad)内平衡点的周期性摆动。
1.3 周期摆动的近似解析解
实际寻北时,陀螺灵敏部作绕[-π rad,π rad)内平衡点的周期性摆动。忽略自摆零位δ,可以认为初始时刻悬带扭力零位方位角与灵敏部主轴方位角重合,即αn=A,则有
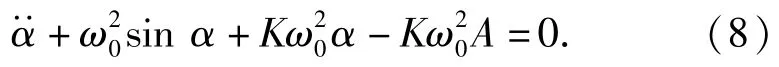
(8)式的恢复力函数不是α的奇函数,给求解带来困难[11-13]。为求其近似解,先对α进行平移变换,令α=x+α*,代入(2)式得
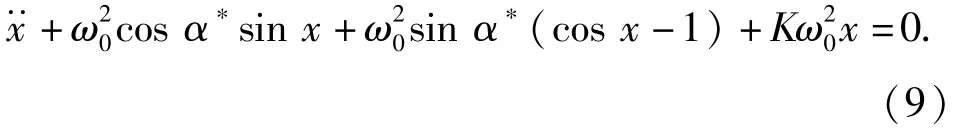
将(9)式中的sinx、cosx展开,并截取到x的二次多项式,得
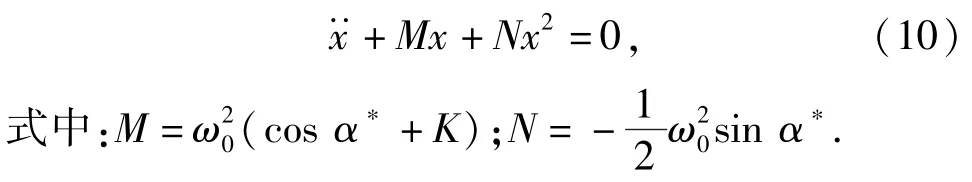
设x的振动区间为[B1,B2],则有

由u(B1)=u(B2)得
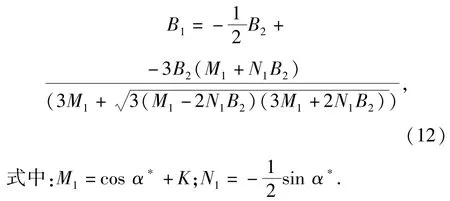
令τ=ωt,将对t的导数写成对τ的导数,则(10)式为
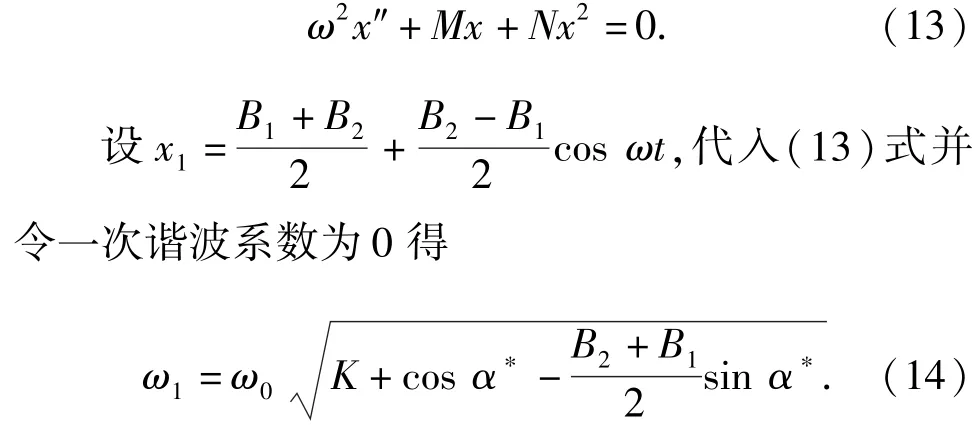
为了获得高阶解析逼近解,根据牛顿法[11],令非线性方程(10)式的近似周期解为
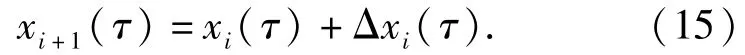
设Δx1(τ)=c1(1-cos 2τ),将x2=x1+Δx1代入(10)式,令常数项和一次谐波系数为0得

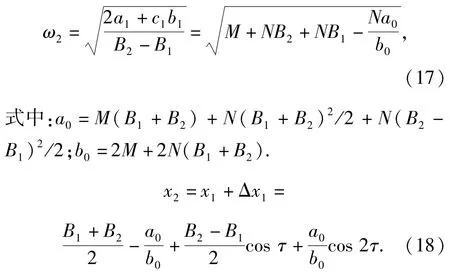
图4显示了1阶逼近解x1、2阶逼近解x2与精确解xe(由数值方法得出)的比较。可以看出1阶逼近已有很好效果,2阶逼近对1阶逼近改进不大,这是因为在悬带的作用下,摆幅被限制在一个较小的范围内。
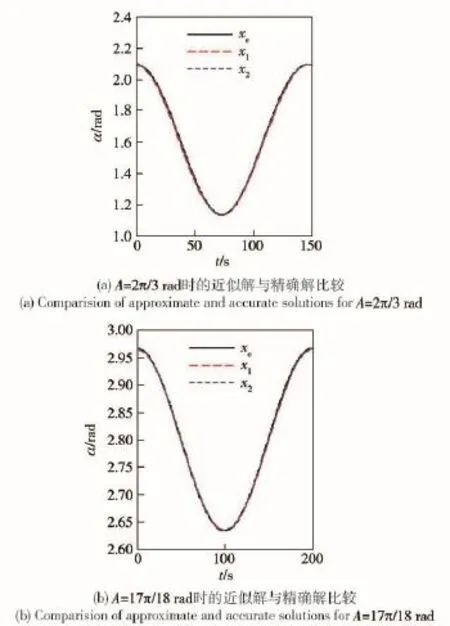
图4 近似解析解与精确解的比较Fig.4 Comparison of approximate analytical solutions with the accurate solution
2 周期-摆幅测量全方位预定向方法
2.1 周期-摆幅法预定向原理
设扭力零位和逆转点位置相同,方位角为A,由(14)式得无阻尼不跟踪情况下有
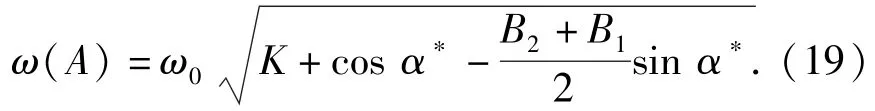
由于B1、B2异号且绝对值相差不大,故B1+B2≪K,将其忽略得
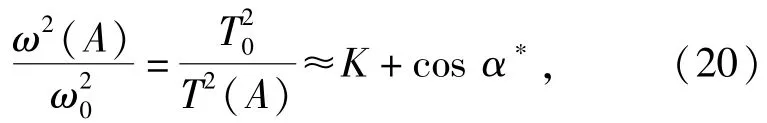
式中:T0=2π/ω0,为陀螺灵敏部跟踪条件下在真北附近的自由摆动周期,可以事先通过试验标定好;T(A)=2π/ω(A),为一定初始架设方位下陀螺灵敏部的实际摆动周期,可以在寻北时通过测量得到。则
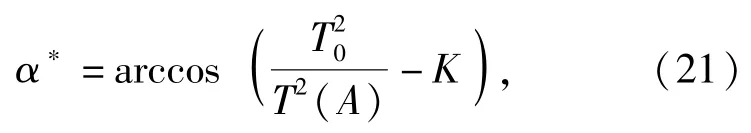
从而
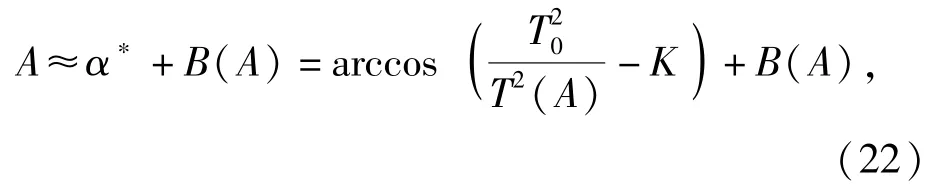
式中:B(A)为陀螺灵敏部的摆动幅度,可以在寻北时通过测量得到。
分别用近似后的周期公式与近似前的周期公式计算不同初始架设方位情况下的无阻尼不跟踪摆动周期,如图5所示。
可以看出二者相差不大,因此可以采用(22)式计算出对应的初始架设方位角。具体步骤是:架设好仪器,启动陀螺马达,待灵敏部摆动到第一个逆转点处时,将扭力零位一步步进至该逆转点处,然后测量步进后的摆动周期和摆幅,带入(22)式计算出此时对应的方位角值,然后控制仪器转过相应角度即可使陀螺主轴位于真北附近,实现预定向。该方法仪器处于不跟踪状态,摆动周期比跟踪状态下的摆动周期短,测量摆幅和摆动周期只需要半个周期,加上步进前的摆动时间,寻北时间不应超过一个不跟踪周期。根据图5可知正南附近时摆动周期接近3 min,需要寻找进一步缩短寻北时间的方法。
由(19)式得摆动周期为
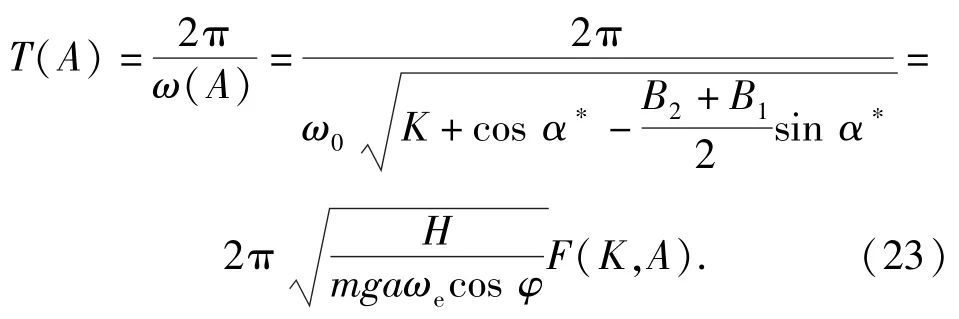
在确定的寻北地点,φ和K不变。从(23)式可知,灵敏部结构参数不变的情况下,在某一架设方位,只能通过减小H缩短寻北时间。由于转子转动惯量一定,所以可以通过降低转速的办法来减小摆动周期。因此,可以采用如下两级启动快速寻北方法实现全方位快速寻北:预定向对精度要求不高,采用低速启动陀螺马达减小摆动周期,缩短定向时间;精寻北时额定转速启动陀螺马达,保证寻北精度。
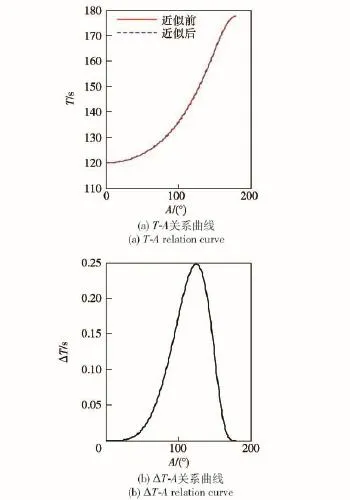
图5 摆动周期随初始架设方位角变化曲线Fig.5 Swing periods at different initial erecting angles
通过(23)式计算得到不同初始架设方位和不同转速时的摆动周期如表1所示。表1中,A为不同的初始架设方位,分别为额定转速、1/2额定转速、1/4额定转速和1/8额定转速时的摆动周期。从表1可以看出,随着初始架设方位的增大,摆动周期变长;额定转速时,真北附近摆动周期约2 min,正南附近摆动周期约3 min;1/4额定转速时的摆动周期为额定转速时的一半,正南附近摆动周期约1.5 min;而1/8额定转速时在正南附近(170°)摆动周期减小到约1 min(62.14 s)。可见预定向时低速启动陀螺马达有效缩短了摆动周期。实际寻北时,粗寻北时启动陀螺马达至1/8额定转速,通过两个逆转点之间的摆动即可测出摆幅和周期,实际的预定向时间将在1/2周期到一个周期之间,最长为62.14 s,不超过65 s.
综合以上分析可得周期-摆幅法的实现流程如图6所示。启动陀螺转子马达至1/8额定转速;转速稳定后下放陀螺灵敏部;灵敏部摆动到第一个逆转点时将悬带零位步进至该逆转点处;测量灵敏部摆动到另一个逆转点处的摆动时间和摆动角度,计算出摆动周期和摆幅;灵敏部摆动到第二个逆转点时将悬带零位步进到第二个逆转点处以消除悬带扭转形变;控制锁放机构锁紧陀螺灵敏部使其停止摆动;根据(22)式计算出第一个逆转点的偏北角,然后计算出第二个逆转点的偏北角;将灵敏部主轴从第二个逆转点处步进至真北附近,完成预定向。
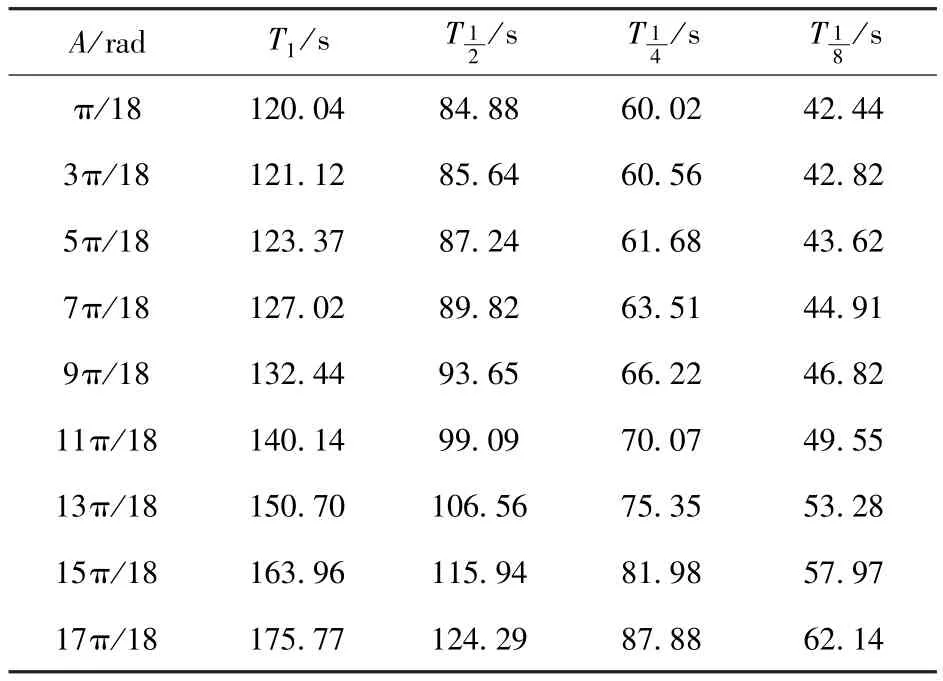
表1 不同转速情况下摆动周期比较Tab.1 Swing periods at different gyro-motor rotating speeds
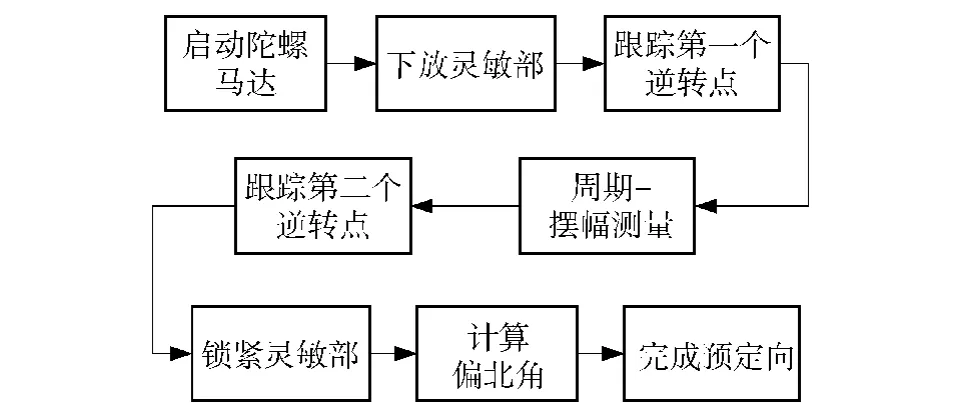
图6 周期-摆幅法预定向流程Fig.6 Flow chart of pre-orientation based on periodamplitude measuring
2.2 误差分析
根据(22)式知预定向精度受T0、T(A)、K、B(A)测量精度的影响,另外由于(22)式为近似公式,会带来方法误差。下面分别分析其对预定向的影响。
2.2.1 方法误差
方法误差由近似化处理引入,对各A值,由计算得到的偏北角值与真实值偏差如图7(a)所示。可以看出,推导公式过程中所作近似处理带来的误差很小,预定向时可以忽略。
2.2.2 周期测量误差的影响
计算公式中包含T0和T,其中T0事先标定好,T预定向时测量得到。其误差对预定向结果的影响分别如图7(b)和7(c)所示,可以看出预定向误差随周期误差的增大而增加;T值测量误差对预定向结果的影响比T0值测量误差大,T0误差为0.5 s时将带来0.8°的预定向误差,T误差为0.5 s时将带来1.4°的预定向误差。
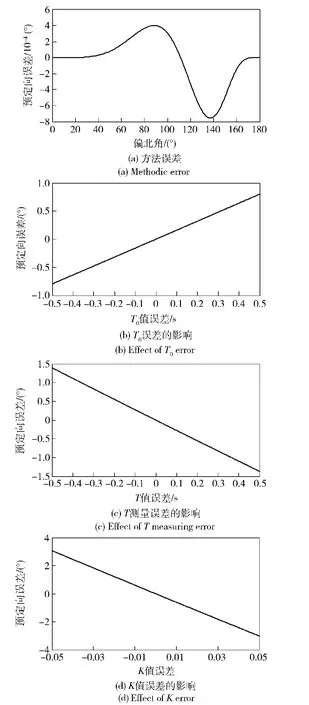
图7 测量误差对预定向结果的影响Fig.7 Effects of different measuring errors on pre-orientation accuracy
2.2.3 K值误差的影响
K值误差对预定向的影响如图7(d)所示,可以看出预定向误差随K值误差的增大而增大,当K值误差为0.05时,预定向误差约为3°.可见,预定向结果对K值误差更为敏感,这是因为其直接影响(21)式右边余弦值的大小。
2.2.4 摆幅测量误差的影响
从(22)式中可以看出,摆幅测量误差对预定向结果的影响呈线性关系,主要受逆转点位置测量准确度的影响。
2.2.5 转位误差的影响
预定向过程中有3次步进,每次步进时电机转位误差也直接影响预定向精度。
实际预定向时,如果通过标定将周期T0的误差控制在0.05 s,K的误差控制在0.01,T值测量误差控制在0.2 s,则其带来的预定向误差分别为0.1°、0.6°、0.6°;若摆幅测量误差为0.5°,转位误差为1′,则总的预定向误差约为1°,可以保证在5°以内。
2.3 试验验证
为验证本文所提方法的可行性,在实验室中的寻北定向综合试验系统上进行试验验证,试验系统组成如图8所示。
该试验系统主要由摆式陀螺寻北仪、数据采集模块、主控计算机和外围电路组成。数据采集模块主要由Agilent 34401A数字万用表和SDG1025数字信号发生器组成。摆式陀螺寻北仪由摆式陀螺仪、经纬仪、寻北控制盒等组成,由配套的控制盒控制陀螺寻北仪进行寻北;寻北控制盒内置完整的自动寻北流程,定向精度5″,要求初始架设方位在真北方向±20°以内;寻北控制盒还内置手动控制模式,可以控制寻北仪单独实现粗寻北、自摆零位测量、限幅、精寻北、锁放、跟踪等操作;两种模式下均可以通过修改控制程序实现对不同寻北方法的研究。
按照图6所示寻北流程编制粗寻北控制程序,依次使初始架设方位位于东北、东、东南、南、西南、西、西北7个位置附近(依次用1~7表示),首先进行预定向,预定向后进入内置的自动寻北流程,将预定向输出结果与最终寻北结果比较计算预定向误差,试验结果如表2所示。

图8 寻北定向综合试验系统组成Fig.8 System composition of synthetical test stand for north finding

表2 周期-摆幅法预定向试验结果Tab.2 Pre-orientation results based on period-amplitude measuring
从表2可以看出,采用周期-摆幅测量法可以实现全方位预定向,预定向误差最大不超过5°;预定向时间介于1/2摆动周期到一个摆动周期之间,随着初始架设方位的增加而呈增大趋势;预定向时间最长为48 s,不超过65 s,与理论分析结果一致,满足快速寻北要求。
3 结论
本文针对现有摆式陀螺寻北仪普遍存在的对初始架设方位要求严格的问题,在详细分析其大偏北角运动规律的基础上,提出了一种基于周期-摆幅测量的全方位快速预定向方法。分析结果表明:采用周期-摆幅测量法预定向,能够实现全方位寻北,有效克服了传统磁罗盘全方位预定向易受干扰、难以保证可靠性的不足;预定向时低速启动陀螺马达能有效缩短寻北时间,提高寻北效率,使预定向时间不超过65 s;预定向精度受各种误差的影响,一般能够控制在5°以内,满足后续限幅、精寻北等过程的精度要求。由于寻北仪的精度主要取决于后续的精寻北过程,因此该方法配合相应的限幅和精寻北方法,能够在不显著增加寻北时间的基础上使现有各种精度的寻北仪实现真正意义上的自主全方位寻北,摆脱对磁罗盘等辅助设备的依赖,提高系统的可靠性和使用灵活性。
(
)
[1]薛海建,郭晓松,周召发.一种任意二位置陀螺寻北模型及其数据处理技术[J].兵工学报,2014,35(4):559-566. XUE Hai-jian,GUO Xiao-song,ZHOU Zhao-fa.Model and data processing of arbitrary two-position north finder[J].Acta Armamentarii,2014,35(4):559-566.(in Chinese)
[2]Rommel N.Functional principle and technical concept of the highprecision surveying gyroscope GYROMAT-2000[C]∥Symposium on Gyro Technology.Stuttgart,Germany:Deutsche Gesellschaft für Ortung und Navigation,1994.
[3]杨玉含,黄先祥,周召发,等.基于电子罗盘的快速粗定向方法研究[J].计算机测量与控制,2012,20(3):768-770. YANG Yu-han,HUANG Xian-xiang,ZHOU Zhao-fa,et al. Method research of quickly coarse orientation based on electronic box and needle[J].Computer Measurement&Control,2012,20(3):768-770.(in Chinese)
[4]田育民,刘思伟,白云超.摆式陀螺经纬仪粗寻北的新方法[J].中国惯性技术学报,2009,17(4):441-448. TIAN Yu-min,LIU Si-wei,BAI Yun-chao.New method of rough north seeking applied in gyro-theodolite[J].Journal of Chinese Inertial Technology,2009,17(4):441-448.(in Chinese)
[5]张志利,陈河,周召发.摆式陀螺复合式全方位快速寻北[J].光学精密工程,2013,21(12):3072-3079. ZHANG Zhi-li,CHEN He,ZHOU Zhao-fa.Complex rapid omnibearing north seeking of pendulous gyroscope[J].Optics and Precision Engineering,2013,21(12):3072-3079.(in Chinese)
[6]王振业,郭晓松,周召发,等.摆式陀螺寻北仪的大偏北角运动特性分析[J].压电与声光,2013,35(2):204-208. WANG Zhen-ye,GUO Xiao-song,ZHOU Zhao-fa,et al.The motion characteristics in large azimuth of the pendulous gyroscope north-seeker analyzing[J].Piezoelectries&Acoustooptics,2013,35(2):204-208.(in Chinese)
[7]陈河,张志利,周召发,等.摆式陀螺大偏北角运动特性研究[J].电光与控制,2013,20(12):56-59. CHEN He,ZHANG Zhi-li,ZHOU Zhao-fa,et al.Research on motion characteristics of pendulous gyroscope in large azimuth[J].Electronics Optics&Control,2013,20(12):56-59.(in Chinese)
[8]Dong G M,Zhang W Y,Lin Y C.Study on automated gyrotheodolite based on unified north-finding algorithm[C]∥2nd International Conference on Materials,Mechatronics and Automation.Nanchang,China:IEEE,2012:931-935.
[9]Xie M J,Li L T,Wang Z Q.Study and application of variable period sampling in strap-down north seeking system[J].Energy Procedia,2012,16:2081-2086.
[10]Zhou Z F,Chang Z J,Zhang Z L.A new rapid north-seeking method of pendulous gyroscope[C]∥International Conference on Measurement,Information&Control.Harbin,China:IEEE,2012:173-176.
[11]李鹏松,孙维鹏,吴柏生.单摆大振幅振动的解析逼近解[J].振动与冲击,2008,27(2):72-74. LI Peng-song,SUN Wei-peng,WU Bai-sheng.Analytical approximate solutions to large amplitude oscillation of a simple pendulum[J].Journal of Vibration and Shock,2008,27(2):72-74.(in Chinese)
[12]Bayat M,Pakar I.On the approximate analytical solution to nonlinear oscillation systems[J].Shock and Vibration,2013,20(1):43-52.
[13]Hermann M,Saravi M,Khah H E.Analytical study of nonlinear oscillatory systems using the Hamiltonian approach technique[J].Journal of Theoretical and Applied Physics,2014,8(3):1-8.
Omni-bearing Fast Pre-orientation of Pendulous Gyroscope Based on Period-amplitude Measuring
CHEN He,ZHANG Zhi-li,ZHOU Zhao-fa,ZHAO Xiao-feng
(The Second Artillery Engineering University,Xi'an 710025,Shaanxi,China)
A novel omni-bearing pre-orientation method based on period-amplitude measuring is put forward through the analysis of motion characteristics of pendulous gyro north seeker in wide azimuth.The proposed method can be used to calculate the azimuth of the gyro shaft by measuring its swing period and amplitude.The effect of gyro-motor rotating rate on pre-orientation time is analyzed,the effect of pertinent parameter errors on pre-orientation accuracy is discussed,and the preliminary experiments are conducted to verify the new method.Both the theoretical and experimental results show that the swing period can be shortened by decreasing the rotating speed of the gyro-rotor,and the rapid pre-orientation can be achieved accordingly within 65 s with the accuracy of higher than 5°,which can meet the accuracy requirement of subsequent north seeking procedures.
ordnance science and technology;pendulous gyroscope north seeker;wide azimuth;omnibearing north-seeking;period-amplitude measuring
TH761;U666.1
A
1000-1093(2015)08-1458-08
10.3969/j.issn.1000-1093.2015.08.012
2014-12-19
国家自然科学基金项目(41174162、41404022)
陈河(1989—),男,博士研究生。E-mail:496076391@qq.com;张志利(1966—),男,教授,博士生导师。E-mail:zhangzl202@126.com

