涡环旋转伞充气过程及气动特性分析
马晓冬,郭锐,刘荣忠,吕胜涛
(南京理工大学智能弹药技术国防重点学科实验室,江苏南京210094)
涡环旋转伞充气过程及气动特性分析
马晓冬,郭锐,刘荣忠,吕胜涛
(南京理工大学智能弹药技术国防重点学科实验室,江苏南京210094)
为了探索灵巧子弹药的减速导旋伞——涡环旋转伞的充气性能和气动特性,利用任意拉格拉日-欧拉流-固耦合方法,模拟一种典型涡环旋转伞在无限质量和低速气流条件下的充气过程,得到伞衣动态变化过程、转速和投影直径时程变化曲线及充满后稳态下的流场变化特性。将充满伞衣幅的有限元模型转化为气动特性仿真模型,利用计算流体力学方法得到涡环旋转伞在低速气流作用下的气动力参数及流场流线、压力分布等特性。将两种方法得到的结果进行对比分析,结果表明:涡环旋转伞在来流12 m/s时能顺利充气展开并实现旋转,伞衣幅充满外形饱满,稳定转速约为3.3 r/s;阻力系数为1.36,大于一般结构轴对称降落伞;导旋力矩系数为0.87;流场分布具有中心对称性。
兵器科学与技术;涡环旋转伞;开伞过程;流-固耦合;计算流体力学;气动特性
0 引言
涡环旋转伞是一种常见的旋转降落伞,由于伞衣的高速旋转,使带有涡环旋转伞的物伞系统在下落过程中具有良好的运动稳定性[1]。此外,它还具有开伞动载小、成本低、易维护等优点,被广泛应用于兵器的弹道控制、航空航天等领域[2-3]。近年来,涡环旋转伞常作为灵巧弹药的减速导旋伞,可有效提高灵巧弹药在弹道末端的运动稳定性,从而进一步提升命中率。
降落伞的可靠充气是其正常工作的前提,但该过程涉及流-固耦合(FSI)、瞬间大变形结构动力学问题,物理过程最为复杂。近年来,国内外学者通过数值计算对降落伞的充气进行了大量研究。文献[4]针对末敏弹减速装置采用的平面圆伞,考虑伞衣结构内力和内部气流运动,建立充气过程的粒子节点动力学模型。文献[5]采用浸入边界法计算了三维模型伞开伞情况。文献[6-7]采用任意拉格拉日-欧拉(ALE)方法模拟降落伞的开伞过程,得到开伞充满时间和伞形的变化,给出了织物材料模型、风洞降落伞分析、降落伞充气研究及与空投试验的对比。降落伞充满后做下落运动,其气动特性影响着伞物系统的运动规律,同时,其气动力参数是降落伞系统稳定性研究和弹道计算的重要参数。与研究降落伞充气过程的FSI方法不同,研究物体气动特性、计算气动力参数主要利用计算流体力学(CFD)方法。文献[8]应用CFD方法对灵巧子弹系统进行亚声速范围气动仿真,得到伞弹阻力系数、升力系数和俯仰力矩系数,并与风洞试验进行了对比。文献[9]基于有限体积法和SST湍流模型对飘带伞和平头子弹组成的伞弹系统进行超声速数值模拟,采用数值纹影法显示流场分布,得到伞弹的阻力系数。综上,降落伞的已有研究多关注于轴对称的平面圆形或锥形等降落伞,对旋转降落伞尤其是涡环旋转伞的充气过程、气动特性等相关研究还有待探索。
本文以一种典型的涡环旋转伞为研究对象,结合FSI方法和CFD方法,对其充气过程及充气完成后的气动特性进行研究。首先建立初始充气模型,利用FSI方法模拟其充气展开过程,得到充气过程中伞衣动态变化过程、转速和投影直径等变化曲线,及稳态时的流场衍变规律;将FSI计算得到的充满伞衣幅有限元模型转化为气动特性仿真模型,进行CFD分析。
1 FSI计算模型
1.1 涡环旋转伞
图1(a)为涡环旋转伞展开后的几何模型,主要由4片伞衣幅和33根不同长度的伞绳组成。图1(b)为其平面展开图,伞衣幅展开为非轴对称的平面曲边七边形,伞衣幅之间关于伞轴中心对称排布。
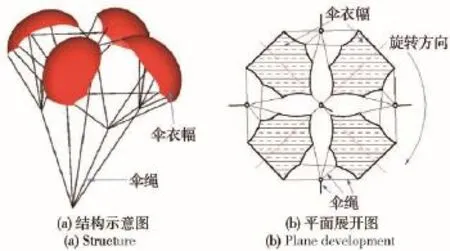
图1 涡环旋转伞结构示意图Fig.1 Configuration of vortex ring parachute
1.2 有限元模型
将伞衣幅建立成平面,2 892个二维壳单元划分网格,围绕伞轴按中心对称方式排布;679个绳索单元划分伞绳,并折叠至合适的长度,与伞衣幅连接[10];612 128个六面体实体网格划分流场。有限元模型如图2所示,限制边绳和中心绳交汇点的3个平移自由度,但不限制该点的转动,为无限质量充气情况;考虑到涡环旋转伞稳定下落速度范围为8~20 m/s,且为了方便下文对仿真结果的验证,设定来流速度为12 m/s;流场入口采用速度入口边界条件,流场其余边界采用无反射边界条件,涡环旋转伞位于流场中央位置;伞衣幅织物和伞绳的材料参数见文献[10],考虑伞衣幅的透气性。
为了使涡环旋转伞充气初始模型接近实际情况的“束状”,首先利用ALE方法[11-14]对图2(a)中模型进行FSI计算,当伞衣幅的形状变为如图2(b)所示时,约束伞衣节点的平移自由度,使伞系统转速为0,将此时模型作为涡环旋转伞充气模型的初始状态,重新进行耦合计算。
2 充气过程
涡环旋转伞充气过程如图3所示。开始阶段,气流主要作用于伞衣外缘,伞衣幅相互间发生轻微的靠拢,伞投影直径d减小,如图4所示。同时由于伞衣幅与气流作用表面具有一定的倾斜度,所以伞立即发生转动,如图5所示。随后,伞衣幅开始充气展开,伞投影直径急剧增大;伞衣幅从收拢状开始展开的一小段时间内,与其连接的伞绳没有拉直,使得伞衣幅没有形成较明显的倾斜度,故伞转速有所下降。约t=0.20 s时,各伞绳基本拉直,伞投影直径继续增加,伴随着伞转速快速提升。约t=1.24 s时,伞投影直径达到1.46 m且不再明显变化,说明涡环旋转伞充气完成。充满的伞衣幅形成凸面,与水平面间具有较大的倾斜度,在来流的作用下形成沿伞轴方向中心对称的力矩,使涡环旋转伞加速旋转。约t=2.10 s时,伞转速达到3.30 r/s且不再明显变化,达到稳定状态。仰视下落的涡环旋转伞系统,其逆时针旋转。
由于4片伞衣幅之间具有很大的空白区域,即结构透气量大,因此涡环旋转伞没有明显的初始充气阶段和主充气阶段,也没有明显的“呼吸现象”。充气过程中,靠拢的伞衣幅首先分散开,在气流和伞绳拉力作用下张满,类似“船帆”。涡环旋转伞充气完成后,绕伞轴平稳地旋转,伞轴没有明显的晃动,说明涡环旋转伞具有良好的运动稳定性。

图2 FSI有限元模型Fig.2 Finite element model of FSI
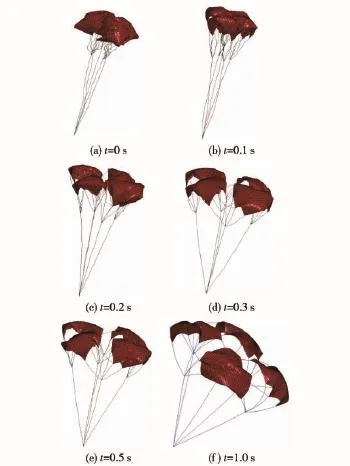
图3 涡环旋转伞充气过程Fig.3 Inflation process of vortex ring parachute
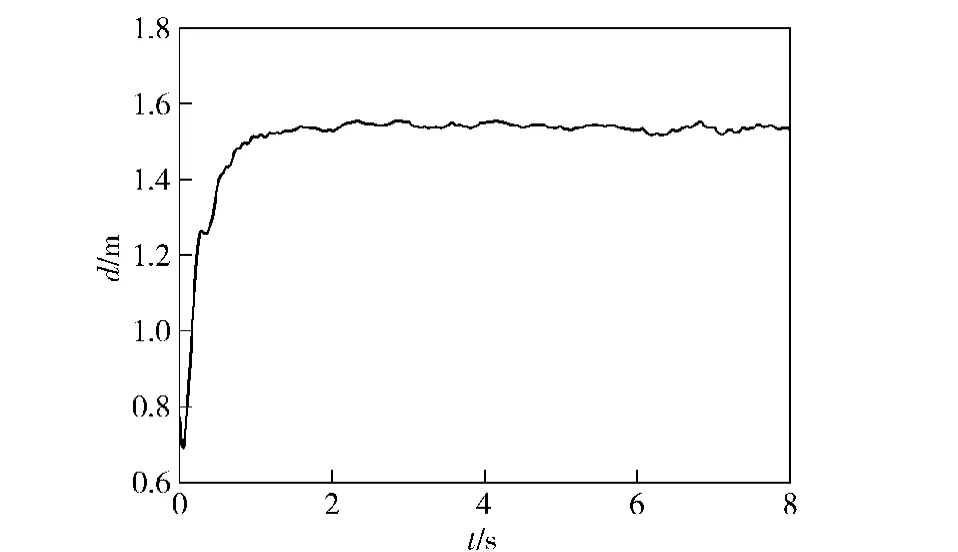
图4 伞衣投影直径Fig.4 Projective diameter of canopy
涡环旋转伞转速和伞衣幅外形的仿真结果和试验结果对比如图5和图6所示,其中伞塔试验设计及实施见文献[15]。图5得到:伞塔试验中,涡环旋转伞的稳定转速ω在3.3 r/s上下浮动,稳定落速为11.02 m/s,误差为8.2%,这是由于横风、模型制造误差等因素的影响。图6得到:试验中涡环旋转伞的充满外形与仿真结果基本一致,伞塔投放过程中,空中存在横风,导致两片伞衣幅外缘有相对较大的变形。
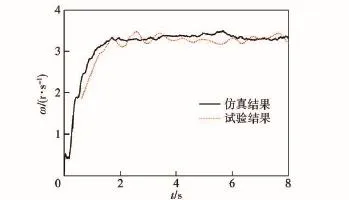
图5 系统转速Fig.5 Spinning rate
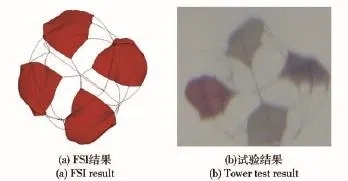
图6 充满时伞衣幅形状Fig.6 Shapes of canopies
综上,伞塔试验数据与仿真结果吻合良好,结合充气初始模型与实物模型初始状态具有较好的一致性,认为利用ALE方法可准确地模拟涡环旋转伞的开伞充气过程。
3 CFD计算模型
为了得到涡环旋转伞稳定条件下的流场特性及主要气动力参数,建立其CFD计算模型。
FSI计算得到的伞衣幅充满状态如图3(f)和图6(b)所示,利用LS-PrePost软件将其有限元模型转化为实体模型,如图7所示,进而构建CFD流场模型。由于伞衣幅充满形状为复杂的曲面,结构化网格划分流场较困难,故采用非结构化网格划分流场。
如图8(a)所示,涡环旋转伞流场为圆柱体,为减小流场边界影响,流场径向取20倍伞投影直径。由于伞衣幅厚度只有0.1 mm,采用尺寸0.1 mm的网格划分伞衣幅壁面,如图8(b)所示,远离伞衣幅区域的网格尺寸逐渐变大。网格总数为1 301 683.
计算过程中,湍流模型采用标准k-ε模型,控制方程采用质量守恒方程、动量守恒方程及能量守恒方程。流体采用理想气体,流动模式采用定常流动,流场入口速度12 m/s.对涡环旋转伞采用绝热刚体壁面假设和无滑移边界条件。由于涡环旋转伞充满后外形不再变化,因此将其假设为刚体壁面是合理的。参考面积为涡环旋转伞投影面积,参考长度为涡环旋转伞在伞轴所在平面内投影的高度。

图7 涡环旋转伞充满形状实体模型Fig.7 Geometry model of inflated canopy

图8 CFD模型Fig.8 CFD model
4 气动特性分析
4.1 流场特性
图9(a)为CFD计算伞衣幅附近静态下的流线分布情况。在伞衣幅外缘和伞衣幅间的空白区域,流线分别发生向外和向内的偏转。由于未考虑透气性,其正下方的流体向左或向右偏转从伞衣幅外沿流过。伞衣幅正上方流体较少。
与图9(a)不同,图9(b)为FSI计算动态过程的流线分布情况:流体从下向上流动,靠近伞衣幅底边外缘的流体向外偏转,绕过伞衣幅,有向外发散的趋势;流向伞衣幅间中央位置的流体向内靠拢,流体速度升高;由于考虑了伞衣材料的透气性,有部分流体穿过伞衣幅表面,其他从伞衣幅外沿流过。由于伞衣幅的结构非对称性且时刻发生转动,其上方流体变化较乱,流线方向随着位置变化很大。忽略伞衣幅上方较远空间位置,两种计算方法得到的伞衣幅附近流场变化情况比较接近,说明了两种方法模拟降落伞附近流场变化情况的正确性。
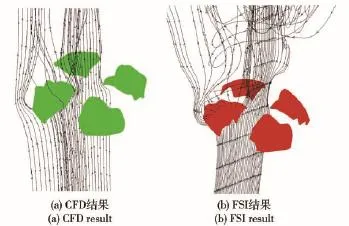
图9 流线图Fig.9 Streamlines
图10为流场压力云图。伞衣幅下表面直接与流动的空气作用,阻止流体通过,故其下方附近压力最高,远离伞衣幅位置的压力逐渐减小至标准气压;气流绕过伞衣幅向上流动,伞衣幅上表面附近流体少,且外沿附近流体速度高,导致伞衣幅上方出现明显的负压。伞衣幅上下表面附近的压差为涡环旋转伞提供阻力。充满稳定阶段,气流在伞衣幅上方形成涡旋,由于结构中心对称性及伞的旋转,涡旋在伞轴所在平面及其垂直平面时刻存在,且随着气流逐渐上升,涡旋中心连线如图11所示。大量涡旋产生涡阻,使得在同等条件下,涡环旋转伞受到的阻力大于其他轴对称结构的降落伞,即涡环旋转伞具有更大的阻力系数。
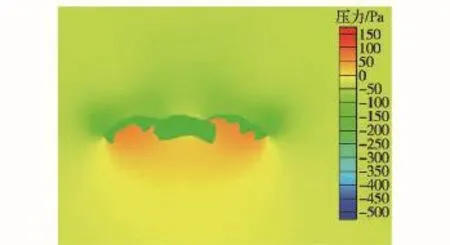
图10 流场静压力云图(CFD方法)Fig.10 Static pressure contour of fluid domain
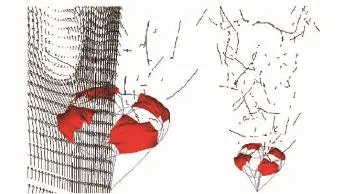
图11 涡旋中心连线(FSI)Fig.11 Composite diagram of velocity vectors and vortex cores
4.2 气动力参数
FSI方法可通过输出开伞动载来计算涡环旋转伞的阻力系数,而CFD方法可直接输出其主要气动力参数。
来流速度12 m/s时的开伞动载曲线如图12所示。由于涡环旋转伞的结构透气量很大,因此其开伞动载一直较平稳地增加,当伞充满后逐渐增大至最大值。由最大开伞动载计算公式[1]:
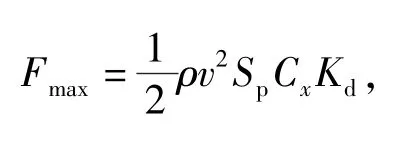
式中:ρ为空气密度;v为风速;Kd为动载系数(无因次),涡环旋转伞的动载系数在无限质量条件下约1.0[16];Sp为特征面积;Cx为阻力系数。开伞动载最大值约150 N,取4片伞衣幅的投影面积1.30 m2为特征面积,得涡环旋转伞的阻力系数为1.31.
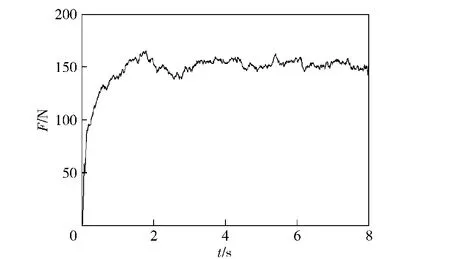
图12 开伞动载(FSI方法)Fig.12 Opening load
CFD计算得到涡环旋转伞的阻力系数为1.36,略大于1.31,误差为3.8%,主要是由于算法、网格的差异及伞衣幅透气性的影响。另外CFD可得导旋力矩系数为0.87,攻角为2°时升力系数为0.02.
5 结论
1)涡环旋转伞具有非轴对称结构,其伞衣幅在低速气流作用下充气展开后形成凸面,与水平面间有一定的倾斜度,可实现旋转性能;结构透气量大,充气过程没有明显的初始充气过程和主充气过程,也没有明显的“呼吸现象”。
2)伞衣幅间空隙及外缘附近的流体速度高;4片伞衣幅中心对称及转动使得其上方流场产生连续的涡旋;伞衣幅对流体的阻滞作用及大量涡旋产生的涡阻,使得涡环旋转伞的阻力系数大于一般其他轴对称降落伞。
3)FSI和CFD方法相结合,可输出涡环旋转伞主要气动力参数:阻力系数、升力系数和导旋力矩系数,可用于涡环旋转伞-子弹系统的弹道计算和运动稳定性分析。
4)应用FSI方法可模拟涡环旋转伞的开伞过程,得到伞衣变形情况、转速和投影直径变化等动力学响应,及稳态下的流场动态变化规律;对结果进行处理,输出稳态外形有限元模型的单元节点信息,转化为CFD仿真模型,研究其气动特性。此研究流程方法可用于各类型伞和柔性装置的设计优化:当动力学特性及气动特性不满足设计要求时,可微调柔性研究对象的结构,重复上述计算流程。
(
)
[1]王利荣.降落伞理论与应用[M].北京:宇航出版社,1997. WANG Li-rong.The theory and application of parachute[M]. Beijing:China Astronautics Publishing House,1997.(in Chinese)
[2]Ewing E G,Bixbu H W,Knacke T W.Recovery systems design guide,AD A070251[R].Gardena,CA:Irvin Industries Inc,1978.
[3]Guo R,Liu R Z.Dynamics model of the rigid and flexible coupling system for terminal-sensitive submunition[J].Journal of China Ordnance,2007,28(1):10-14.
[4]殷克功,刘荣忠,徐刚,等.末敏弹减速伞充气过程有限元方法研究[J].系统仿真学报,2009,21(9):2500-2502. YIN Ke-gong,LIU Rong-zhong,XU Gang,et al.Research on drag parachute inflation process of target-sensitivity projectile based on finite element method[J].Journal of System Simulation,2009,21(9):2500-2502.(in Chinese)
[5]Yongsam K,Charles S P.3-D parachute simulation by the immersed boundary method[J].Computers&Fluids,2009,38(6):1080-1090.
[6]Tutt B,Taylor A P.The use of LS-DYNA to simulate the inflation of a parachute canopy[C]∥18th AIAA Aerodynamic Decelerator Systems Technology Conference and Seminar.Munich,Germany:AIAA,2005.
[7]Tutt B,Charles R,Roland S,et al.Development of parachute simulation techniques in LS-DYNA[C]∥11th International LS-DYNA Users Conference.Dearborn,Michigan,US:LSTC,2010.
[8]李尧尧,姜春兰.阻力伞—灵巧子弹系统气动及稳定性研究[J].北京理工大学学报,2014,34(8):785-789. LI Yao-yao,JIANG Chun-lan.Analysis on the aerodynamic characteristics and the stability of parachute-bomb system[J]. Transactions of Beijing Institute of Technology,2014,34(8):785-789.(in Chinese)
[9]完颜振海,冯顺山,董永香,等.超音速伞弹流场特性数值分析[J].兵工学报,2011,32(5):520-525. WANYAN Zhen-hai,FENG Shun-shan,DONG Yong-xiang,et al. Numerical analysis of flow characteristics of supersonic submunition and parachute[J].Acta Armamentarii,2011,32(5):520-525.(in Chinese)
[10]马晓冬,刘荣忠,郭锐,等.涡环旋转伞系统开伞充气过程仿真研究[J].航天返回与遥感,2013,34(2):1-7. MA Xiao-dong,LIU Rong-zhong,GUO Rui,et al.Simulation research on inflation of vortex rotating parachute system[J]. Spacecraft Recovery&Remote Sensing,2013,34(2):1-7.(in Chinese)
[11]Souli M,Ouahsine A,Lewin L.ALE formulation for fluid-structure interaction problems[J].Computer Methods in Applied Mechanics and Engineering,2000,190:659-675.
[12]Aquelet N,Tutt B.Euler-lagrange coupling for porous parachute canopy analysis[J].The International Journal of Multiphysics,2007,1(1):53-68.
[13]David J B.A mixture theory for contact in multi-material eulerian formulations[J].Computer Methods in Applied Mechanics and Engineering,1997,140:59-86.
[14]Aquelet N,Tutt B.Euler-lagrange coupling for porous parachute canopy analysis[J].The International Journal of Multiphysics,2007,1(1):53-68.
[15]郭锐,刘荣忠,胡志鹏,等.涡环旋转伞开伞稳定性及减速导旋稳定性研究[J].空气动力学学报,2013,31(6):733-738. GUO Rui,LIU Rong-zhong,HU Zhi-peng,et al.Study on the inflation stability and motional characteristics of vortex ring parachute canopy[J].Acta Aerodynamica Sinica,2013,31(6):733-738.(in Chinese)
[16]Weese J H,Chernowitz G.气动力减速器原理及设计[M].回返技术翻译组,译.北京:国防工业出版社,1974. Weese J H,Chernowitz G.Performance of and design criteria for deployable aerodynamic decelerators[M].Recovery Technology Translation Group,translated.Beijing:National Defense Industry Press,1974.(in Chinese)
Analysis of Inflation and Aerodynamic Characteristics of Vortex Ring Parachute
MA Xiao-dong,GUO Rui,LIU Rong-zhong,LYU Sheng-tao
(ZNDY Ministerial Key Laboratory,Nanjing University of Science and Technology,Nanjing 210094,Jiangsu,China)
To explore the inflation performance and aerodynamic characteristics of vortex ring parachute which is often used as decelerating and spinning parachute of smart ammunition,the inflation process under the conditions of infinite mass and slow flow velocity is simulated using arbitrary Lagrange-Euler method.The canopy deforming process,time-history curves of spinning rate and projected diameter and fluid domain features at steady state are obtained.The finite model of inflated canopies is transformed to a simulation model of aerodynamic characteristics.The aerodynamic force parameters,the features of velocity streamlines and the pressure distribution are obtained by using computational fluid dynamics method.The results obtained by the two methods are compared and analyzed.The results show that the vortex ring parachute can inflate smoothly and rotateat 12 m/s.The shape of inflated canopy is plump and the steady spinning rate is about 3.3 r/s.The drag coefficient is about 1.36,which is greater than those of other typical parachutes with axial symmetry structure.The spinning moment coefficient is 0.87.The distributions of fluid domain features are centrally symmetrical around the parachute axis.
ordnance science and technology;vortex ring parachute;inflation;fluid-structure interaction;computational fluid dynamics;aerodynamic characteristics
V441.8
A
1000-1093(2015)08-1411-06
10.3969/j.issn.1000-1093.2015.08.006
2014-12-05
国家自然科学基金项目(11102088);江苏省研究生培养创新计划项目(CXLX12_0210)
马晓冬(1988—),男,博士研究生。E-mail:bqnj6222007@126.com;刘荣忠(1955—),男,教授,博士生导师。E-mail:liurongz116@163.com

