重型自动机械变速车辆换挡序列优化
刘海鸥,晋磊,董诗瑾,苗成生
(北京理工大学机械与车辆学院,北京100081)
重型自动机械变速车辆换挡序列优化
刘海鸥,晋磊,董诗瑾,苗成生
(北京理工大学机械与车辆学院,北京100081)
重型车辆在动力性和燃油经济性上有较大的提升空间。分析了配备自动机械变速器(AMT)的重型车辆换挡动力中断特性,在此基础上建立了AMT重型车辆整车模型,并利用动态规划(DP)求解出重型车辆在确定道路下的最优综合性能换挡序列。计算对比原有换挡规律和DP决策下的车辆运行性能,仿真结果表明,通过调整运行耗时和燃油消耗量的加权因子,可以获得兼备动力性和燃油经济性的综合性能最优换挡序列,在保证AMT重型车辆动力性的前提下改善了燃油经济性,对AMT重型车辆的自动控制具有指导意义。
兵器科学与技术;重型自动机械变速车辆;动态规划;换挡序列优化;最优综合性能
0 引言
工程机械、越野车以及重型轮式机动平台等都面临着工作环境复杂,动力性能与续航能力需求高,能量消耗大的问题[1],因此必须考虑其综合性能。军用地面无人平台的研究主要集中在运动规划和环境感知等方向,其控制主要考虑的问题在于无人平台的定位和路径跟踪等[2],但少有人考虑无人平台本身动力性和燃油经济性的研究。目前燃油经济性已经成为汽车行业发展的一个焦点,利用GPS定位、三维道路谱提供的数据改善燃油效率是较常见的方法。
相对于配用其他变速器的平台,配用自动机械变速器(AMT)的重型车辆具有机械结构简单,传动效率较高,使用成本低等特点[3]。然而,AMT的机械结构又决定了其在换挡过程中的动力中断,因此当车辆所处的道路条件为上坡时,AMT换挡过程中离合器分离与接合之间必然存在运行速度的损失[4-5]。常规的换挡规律制定过程中往往忽略换挡过程车速变化,因此针对AMT重型车辆的换挡规律必须考虑换挡过程中的车速变化。目前利用动态规划解决车辆控制优化的例子较多,例如利用动态规划(DP)算法求解混合动力或电动汽车的能量管理策略、换挡控制策略等[6-7],针对重型卡车的综合性能,利用模型预测控制方法、DP算法的换挡规律优化[8-10]。本文探索了利用道路坡度信息来降低AMT重型车辆在行驶过程中的燃油消耗量和行进耗时的可能性。利用DP求解具有3个状态变量、两个决策变量的综合性能优化问题,以行驶一定路程的运行耗时和所消耗的燃油量的加权和作为目标函数求解出动力性和燃油经济性综合性能最优的换挡序列。
1 AMT重型车辆系统建模
该重型车辆配备了大功率柴油发动机,具备6轮全驱功能,主变速器提供了5个挡位,副变速器采用行星齿轮系统提供2个挡区,该AMT共提供9个前进挡位,满足了其最高设计时速110 km/h和最大爬坡度60%的需求。其传动系统的结构简图如图1所示,车辆系统相关参数见表1.
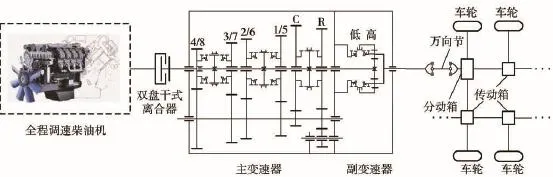
图1 AMT重型车辆传动示意图Fig.1 Transmission diagram of heavy-duty vehicle with AMT

表1 车辆系统参数Tab.1 Vehicle system parameters
根据发动机的测试试验,获取了发动机扭矩特性MAP和燃油消耗率曲线。图2所示为根据该发动机负荷特性绘制的万有特性曲线。发动机的输出扭矩如(1)式所示,其具体值则通过查表插值获得。

式中:Te为发动机扭矩(N·m);ne为发动机转速(r/min);thro为油门开度(%)。根据万有特性曲线可以查取不同扭矩和转速下对应的燃油消耗率,进而求出一段时间内的燃油消耗量,具体见(2)式和(3)式。式中:b为燃油消耗率(g/(kW·h));mt为燃油消耗量(g);[t0,tf]为一段时间间隔。

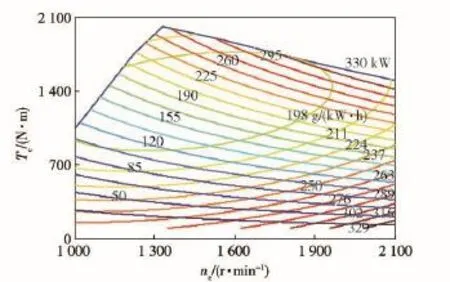
图2 发动机万有特性曲线Fig.2 Universal characteristics of engine
针对传动系统的建模,可将运动部件视为集中质量的刚体,忽略传动系统中温度的影响和轴的横向振动等,根据牛顿第二定理,可得发动机的动力学模型为
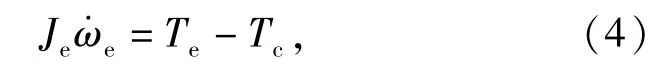
式中:Je为发动机至离合器主动部分的转动惯量(kg·m2);ωe为发动机转速(rad/s);Tc为离合器传递的扭矩(N·m)。AMT在挡运行时,满足发动机转速等于变速器输入轴转速的条件,若不考虑车轮打滑,则在挡时(5)式~(7)式成立。针对车辆的整车模型,主要考虑车辆行驶过程中外部阻力,各个阻力可表达为

式中:i和ηT分别表示在挡位ge时传动系统的总传动比和机械效率;ωw为车轮的转速(rad/s);ve为车辆运行的速度(m/s);rw为车轮滚动半径(m);Fo为作用于车轮上的驱动力(N);Fr为滚动阻力(N);m为该车辆总质量(kg);g为重力加速度(m/s2);f为道路滚动阻力系数;α为道路坡度角(rad);Fa为无风时的空气阻力(N);CD为空气阻力系数;A为迎风面积(m2);ρ为空气密度(kg/m3);Fg为坡道阻力(N)。参照车辆运动方程,在不考虑制动的情况下,可得该车辆加速度与驱动力、各个阻力的关系为
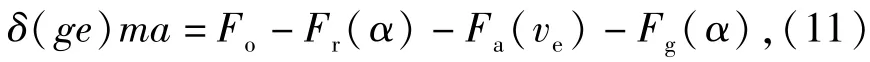
式中:a为车辆加速度(m/s2);δ为旋转质量转换系数。
2 最优综合性能换挡序列求解
本文针对已知坡度的道路,利用DP算法求解出AMT重型车辆在一定路程内行驶时平均运行速度和燃油消耗量加权最优的换挡序列。
DP是解决多阶段决策问题的一种方法,重型车辆在一定路程L内的综合性能最优换挡序列的求解,则可以看作求解一系列车速和挡位下,随着时间变化,换挡指令和油门开度的一系列阶段性决策。
2.1 主要概念的确定
针对该优化问题,首先需要确定出模型的阶段、状态变量、决策和策略、状态转移、指标函数等。按照空间特征将总路程等分为N个相互离散的阶段,每个阶段的步长(距离)为h(m),那么有L=N×h.另外,以k作为不同阶段的阶段变量,k=1,2,…,N.选择阶段k内的运行速度ve、挡位ge和道路坡度α作为相应阶段的状态变量,阶段k的一组状态变量可以表示为sk,如(12)式所示。
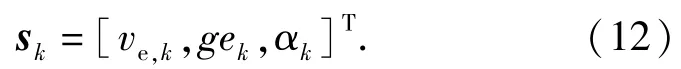
根据重型车辆的特点,考虑无制动的纵向控制,选取的决策变量为换挡指令ug和油门开度ut.第k阶段决策变量如(13)式所示。
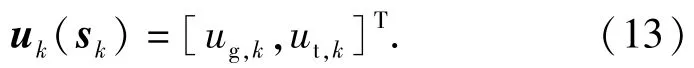
下一个阶段的状态变量sk+1与当前阶段状态变量sk和当前阶段决策uk(sk)的关系称为状态转移方程。本优化问题中的状态变量运行速度ve和挡位ge,其状态转移方程参照(14)式、(15)式,其中加速度ak由(11)式计算获得。道路坡度α由GPS定位和三维地图共同确定,不考虑其状态转移关系。

指标函数分为阶段指标函数和过程指标函数。在保证重型车辆动力性能的前提下尽可能降低燃油消耗,选用每个阶段的运行耗时tk(s)和阶段油耗量ms,k(g)的加权和作为阶段指标函数,所有阶段的指标函数总和作为全局指标函数值[11]。由于运行耗时和阶段油耗的数量级水平相同,故选用归一化加权因子,运行耗时的加权因子选为fβ∈(0,1),则阶段油耗量的加权因子为1-fβ,(16)式所示为本优化问题的阶段指标函数。

式中:

2.2 变量约束
考虑到该重型车辆的运行环境较为复杂,除了常规的铺装道路上运行速度较高外,陡坡爬行等工况下运行速度很缓慢,因此其运行速度ve范围较广,其取值范围可以表示如下:

式中:vmin和vmax分别表示允许的最小和最大运行速度。相应地,不同速度对应于不同的挡位和发动机转速。本重型车辆配备的发动机怠速为600 r/min,最高空载转速2 300 r/min,其理想工作转速在2 100 r/min以下,考虑到DP计算的可行性,将发动机转速限制如下:

该AMT为9挡有级式变速器,其换挡序列所允许的挡位变化除了顺序升降挡外,还需要考虑重型车辆不同载重、极端道路条件下的阻力变化,进而需要跳降挡和跳升挡,本优化问题不考虑制动过程的影响,故设定最多允许跳降3挡,跳升2挡,故挡位ge和换挡指令ug的约束如(21)式、(22)式所示。

为了限制AMT的换挡频率,保证动力中断之后速度损失有足够时间恢复,规定相邻两次换挡过程之间时间间隔约为3 s.如果上一个阶段换挡指令ug,k-1不为0,且当前阶段耗时满足1.5 s<tk<3.0 s,那么当前阶段的换挡指令赋值为ug,k=0.如(23)式所示,利用阶段耗时tk对换挡指令ug,k进行约束。

决策变量中的油门开度ut也有一定限制,即0~100%,为了便于建立DP的变量网格,规定每5%为一个间隔,故油门开度ut的约束表示如下:

2.3 优化模型建立及动态规划算法的实现
根据模型中主要参数的定义和变量约束,可以确定该优化问题的数学模型,(25)式表示优化目标在于求解最优的决策变量序列,使得系统全局的指标函数值J取得最小值。各约束条件参照上文。
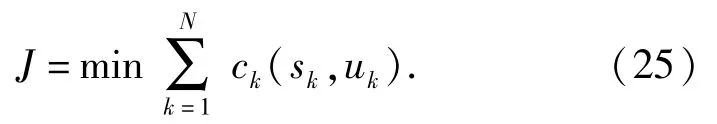
本优化问题选用逆序计算方法,从第N阶段开始进行计算,根据该阶段所有可能的状态和决策计算所有可能的指标函数值,通过比较确定出最优的阶段指标函数值及其对应的状态变量和决策。随后,阶段号k逐次递减并搜索当前阶段所有状态变量中满足状态转移关系的特定状态变量,基于此状态变量和相应的决策再次计算该阶段的最优指标函数,根据状态转移关系累加该阶段及之后所有阶段的最优指标函数值并确定最优的过程指标函数值、状态轨迹和策略,依此类推直到k=1,从而确定出最优状态轨迹和最优策略。
2.4 状态变量预处理及算法改进
2.4.1 变量网格简化
按照上述流程进行一次全局优化的计算量可能相当巨大,为了提高计算效率,分别对状态变量和决策变量简化变量网格。
划分好阶段个数N后,各个阶段的道路坡度α就唯一确定了,而运行速度ve和挡位ge是不确定的。根据发动机转速范围和不同挡位的总传动比可以确定出每个挡位下的运行速度范围,删除运行速度在该范围之外的所有取值。图3为三维的状态变量示意图,在每个阶段中都包含了挡位和速度的二维组合,即图中的网格交点,阶段k里圆圈表示简化后的状态变量网格。
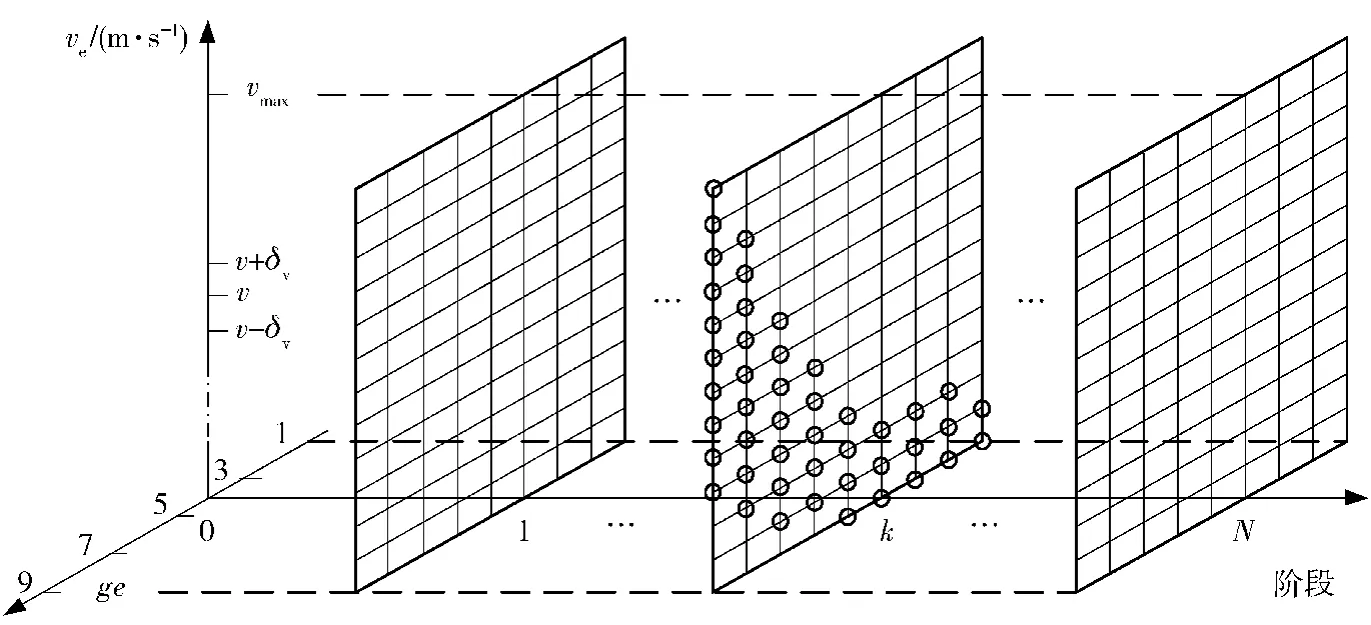
图3 状态变量示意图Fig.3 Grid diagram of state variables
关于决策变量的简化,油门开度ut是随机选择的,不进行简化;而换挡指令ug的简化主要依据(22)式和(23)式进行。完成对状态变量和决策变量的简化后,全局优化的计算量将会显著下降。
2.4.2 考虑AMT换挡特性的DP算法改进
本优化问题重点考虑了AMT的换挡特性,即换挡过程中离合器分离与再次接合之间存在动力中断,在此期间发动机与传动系统完全分离,重型车辆依靠惯性继续运行。当车辆在上坡行驶时,换挡必然面临着运行速度的损失。参照文献[12-13],在DP算法中相邻两个阶段如果发生了换挡,即使换挡完成后车辆能提供更大的驱动力,运行速度仍会出现先下降再上升的情况。此时ve的状态转移方程不再参照(14)式,而是将该状态转移分为两个部分,动力中断部分和动力恢复部分。可以简单地认为动力中断部分的驱动力完全为0,则在动力中断时间内车辆仅受到相应阻力的作用。
一般情况下AMT换挡过程的耗时主要与同步器两端速差、离合器两端速差相关。根据大量的实际数据统计,该AMT换挡过程耗时一般在0.5~1.6 s之间,为了便于计算,设定动力中断时间toff= 1.0 s.动力恢复部分是利用剩余的阶段耗时进行速度恢复,与在挡运行时状态转移方程类似。
综上所述,该优化问题中运行速度ve的状态转移方程需要根据当前阶段的决策换挡指令ug来确定,如(26)式~(28)式所示,ug,k=0时状态转移方程与(14)式原理相同;否则分别根据动力中断期间的加速度aoff和动力恢复期间的加速度aon和时间tk-toff进行计算。需要注意的是,如果tk-toff小于0,说明运行速度较快,此时令toff=tk即可。

另外,除了换挡过程中动力性能的差异,也考虑了换挡过程中的燃油效率。通常的做法是用怠速过程的燃油消耗率代替换挡过程中的燃油消耗率[8],但结合本平台自身的特性,换挡过程中发动机转速并未下降至怠速,故动力中断过程中与在挡过程的燃油消耗量差异忽略不计,均使用在挡时的油耗计算方法。
3 换挡序列优化计算及仿真
3.1 加权因子的取值
根据第2节内容,在Matlab中编写算法指令并进行调试,除了主函数外,还包含DP计算程序、状态变量预处理、决策组生成、状态转移搜索、指标函数和验算输出等子函数。在DP的理论计算中,使用该路段总耗时表征动力性,用全局油耗量表征燃油经济性,用全局指标函数值表征综合性能指标,所以运行耗时的加权因子fβ是个很重要的参数,理论上讲,fβ与1-fβ之比越小,则DP决策的结果倾向于越好的燃油经济性,同时动力性越差。但实际计算中,随着fβ的取值增大,DP决策结果中燃油消耗量的变化并不是绝对正相关的。对此,针对某种道路情况和油门开度,选择0.001~0.999之间若干个数值进行计算,并分析随着fβ变化运行耗时与燃油消耗量的变化情况。
为了降低DP全局优化的计算量,选取一段路程1 500 m的小坡度路面进行计算,人为设定重型车辆在该路面上行驶的初始运行速度为13 m/s,初始挡位为7挡,全路段运行速度在13~18 m/s之间,速度离散步长Δv为0.1 m/s,并设定油门开度始终保持在50%.因此,该优化问题是个固定始端的DP,理论计算中使用的参数设置如表2所示,该路段道路坡度随距离的变化关系如图4所示。

表2 参数设置表Tab.2 Parameters setting table

图4 道路坡度图Fig.4 Road slope diagram
根据不同fβ取值计算出的换挡序列,统计其全局运行耗时和燃油消耗量,并绘制出性能指标随着fβ变化而变化的关系曲线,如图5所示分别给出了运行耗时、燃油消耗量以及fβ和(1-fβ)之比(因子比值)。从图5可以看出,在当前的道路条件和油门开度下,随着fβ的增大,运行耗时整体上在减小,而燃油消耗量整体呈增大趋势。但在一定范围内,即使fβ取值改变,DP决策结果不变,则动力性和燃油经济性指标不变。另外,当fβ小于0.77时,燃油消耗量增长幅度较小,而fβ在(0.77,0.91)之间时燃油消耗量小幅度下降;在(0.91,0.975)之间时,运行耗时显著减小,同时燃油消耗量明显增大;在(0.975,1)之间时,两个指标基本稳定,仅有很小幅度的变化。因此,在此油门开度和图4所示道路条件下,选择(0.77,0.91)中的一个数作为fβ取值,可获得更优的综合性能。
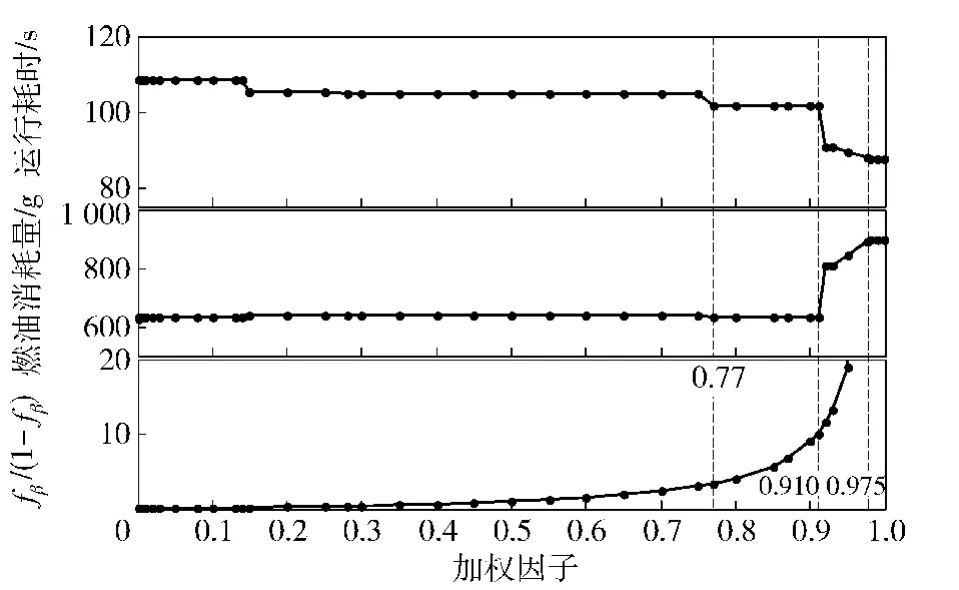
图5 性能指标变化曲线Fig.5 Curves of performance indicators
3.2 DP决策与原换挡规律的性能对比
为了说明DP理论计算出的决策具有最优的综合性能,以原有两参数换挡规律对应的性能作为参照。如图6所示,原车采用的换挡规律以速度和油门开度作为控制参数,且该两参数换挡规律已通过出厂实车测试,满足设计所要求的整车动力性指标。利用模型仿真得到原换挡规律在相同条件下的性能曲线,对比DP决策结果和原换挡规律下仿真结果,即在同一路段内对比车辆运行速度基本一致时的燃油消耗量。部分对比参数设置如表3所示,其中fβ=0.5即根据3.1节所述方法确定得到。

图6 原换挡规律曲线Fig.6 Original shift schedule curves

表3 对比参数设置Tab.3 Parameters setting table
50%油门开度下DP决策和原换挡规律的对比曲线如图7所示,其中实线均为原换挡规律下的曲线,虚线为DP理论计算的结果,对比结果见表4.

表4 50%油门燃油经济性对比结果Tab.4 Comparison of fuel economy with 50%throttle

图7 50%油门DP决策与原换挡规律对比曲线Fig.7 Comparison of DP strategy and original shift schedule with 50%throttle
根据图7和表4,可知当前的油门开度和道路条件下,全局上看DP决策和原有换挡规律跟踪同一运行速度时,能够保证二者具有相同的动力性能,但是DP决策的换挡序列在降速时能够保持较高挡位进而消耗较少燃油,在动力性能不变差的前提下提升了燃油经济性,使燃油经济性和综合性能得到改善和优化。
综上可知,调整fβ取值可以获得最优动力性能或者最优燃油经济性的换挡序列,通过理论计算,发现fβ与1-fβ之比越大,则DP决策的结果倾向于越好的动力性。经过仿真对比基本相同动力性能下的燃油经济性指标,表明DP决策在保证动力性能的前提下能够提升综合性能。
4 结论
针对AMT重型车辆的换挡规律问题,对重型车辆系统建模和换挡特性分析,利用DP对AMT重型车辆换挡序列进行求解,并将DP决策的结果导入Simulink中进行仿真分析。对比DP决策和原两参数换挡规律仿真,通过调整运行耗时和燃油消耗量的加权因子可以获得不同的最优综合性能换挡序列;仿真结果表明,50%油门开度下,DP确定的最优换挡序列在保证AMT重型车辆动力性能的同时,燃油经济性提升了6.65%,对AMT重型车辆的纵向控制具有指导意义。
(
)
[1]余志生.汽车理论[M].第5版.北京:机械工业出版社,2009. YU Zhi-sheng.Vehicle theory[M].5th ed.Beijing:China Machine Press,2009.(in Chinese)
[2]陈慧岩,张玉.军用地面无人平台技术发展综述[J].兵工学报,2014,35(10):1696-1706. CHEN Hui-yan,ZHANG Yu.An overview of research on military unmanned ground vehicles[J].Acta Armamentarii,2014,35(10):1696-1706.(in Chinese)
[3]席军强,丁华荣,陈慧岩.ASCS与AMT的历史、现状及其在中国的发展趋势[J].汽车工程,2002,24(2):89-93. XI Jun-qiang,DING Hua-rong,CHEN Hui-yan.The history and present status of ASCS and AMT and their development trend in China[J].Automotive Engineering,2002,24(2):89-93.(in Chinese)
[4]郭彦颖.重型卡车AMT系统关键技术的研究[D].长春:吉林大学,2010. GUO Yan-ying.Research on key technology for AMT system of heavy truck[D].Changchun:Jilin University,2010.(in Chinese)
[5]郝代.重型车AMT换挡过程动力中断的功率损失特性研究[D].长春:吉林大学,2011. HAO Dai.Research on the power loss characteristics caused by driving force interrupt during shifting process of heavy-duty AMT[D].Changchun:Jilin University,2011.(in Chinese)
[6]Seenumani G,Sun J,Peng H.A hierarchical optimal control strategy for power management of hybrid power systems in all electric ships applications[C]∥49th IEEE Conference on Decision and Control.Atlanta:IEEE,2010:3972-3977.
[7]Xiang Y,Guo L,Gao B.A study on gear shifting schedule for 2-speed electric vehicle using dynamic programming[C]∥25th Chinese Control and Decision Conference.Guiyang:IEEE,2013:3805 -3809.
[8]Hellström E,Ivarsson M,Åslund J,et al.Look-ahead control for heavy trucks to minimize trip time and fuel consumption[J].Control Engineering Practice,2009,17(2):245-254.
[9]Hellström E,Åslund J,Nielsen L.Design of an efficient algorithm for fuel optimal look-ahead control[J].Control Engineering Practice,2010,18(11):1318-1327.
[10]Ivarsson M,Åslund J,Nielsen L.Impacts of AMT gear-shifting on fuel optimal look ahead control,SAE Technical Paper 2010-01-037[R].Pennsylvania:SAE International,2010.
[11]Fu J,Bortolin G.Gear shift optimization for off-road construction vehicles[J].Procedia-Social and Behavioral Sciences,2012,54:989-998.
[12]Ngo V D,Navarrete J A C,Hofman T,et al.Optimal gear shift strategies for fuel economy and driveability[J].Proceedings of the Institution of Mechanical Engineers,Part D:Journal of Automobile Engineering,2013,227(10):1398-1413.
[13]Jacobson B,Spickenreuther M.Gearshift sequence optimisation for vehicles with automated non-power shifting transmissions[J].International Journal of Vehicle Design,2003,32(3):187-207.
Shift Sequence Optimization of Heavy-duty Vehicles with Automated Manual Transmission
LIU Hai-ou,JIN Lei,DONG Shi-jin,MIAO Cheng-sheng
(School of Mechanical Engineering,Beijing Institute of Technology,Beijing 100081,China)
Heavy-duty vehicles have larger space to promote both in dynamic performance and fuel economy. A dynamic model of heavy-duty vehicle equipped with automated manual transmission(AMT)is built based on the analysis of gearshift power interruption.A dynamic programming(DP)method is applied to solve the optimal gearshift sequence in known road condition.The performance comparison between original shift schedule and DP strategy is completed.The simulation results show that the optimal gearshift sequence provides good overall performance,including dynamics and fuel economy,by adjusting the fuel consumption and travel time weighting factor.In addition,the optimal gearshift sequence from DP strategy improves the fuel economy in ensuring the dynamics.
ordnance science and technology;heavy-duty vehicle with automated mannual transmission;dynamic programming;shift sequence optimization;optimal overall performance
U461
A
1000-1093(2015)08-1377-07
10.3969/j.issn.1000-1093.2015.08.001
2014-12-23
武器装备预先研究项目(3030021221505)
刘海鸥(1975—),女,副教授,硕士生导师。E-mail:bit_lho@bit.edu.cn

