一种新型WPT二次侧谐振补偿拓扑

郭 尧 魏 国 宋 凯 逯仁贵 朱春波

（哈尔滨工业大学 哈尔滨 150001）

1 引言

近年来，无线电能传输技术（Wireless Power Transfer,WPT）快速发展，从小功率的手机到大功率电动汽车等均有应用。该技术克服了传统用导线传输电力的诸多局限，使供电更加安全便利，展现出广阔的应用前景[1-3]。

从原理上看，无线电能传输可以分为微波式、激光式、电场耦合式和磁场耦合式几种，其中由于磁场耦合具有辐射低、传输距离适中等特点，因此成为当前的研究热点。

依据原副边线圈与谐振电容的不同连接方式，磁耦合谐振式无线电能传输可以分为串-串、串-并、并-串、并-并四种基本拓扑[4-5]。在此基础上，针对原边又提出了LCL[6]、CLC[7]、SPS[8]等复合型谐振拓扑，而针对副边的谐振拓扑则相对较少，普遍采用的也就是串联谐振和并联谐振拓扑。

假设负载为纯阻性，对于副边并联谐振，其反映到原边的阻抗非纯阻性，因此距离的变化会引起谐振频率漂移。同时，并联谐振等效为电流源特性，因此副边不能空载。相比之下，副边串联谐振反映到原边为纯阻性，具有较好的频率稳定性，同时输出等效为电压源特性，因此系统可以空载运行。尽管如此，受制于其 LC串联的特点，较大的负载值会导致Q值下降，从而降低传输的功率和效率。

本文提出一种用于磁耦合谐振式无线电能传输的新型二次侧谐振补偿拓扑，通过在 LC并联谐振的基础上增加一个T型阻抗变换网络，使其等效为高Q值串联谐振，在具有串联谐振诸多优点的同时，所提出的结构能够在更远的距离实现更大的传输功率和效率。

2 系统理论分析

所提出的WPT拓扑如图1所示，原边为传统的串联谐振，rp为一次侧内阻，为逆变桥内阻与一次线圈线阻的总和。rs为二次线圈线阻，M为一次线圈与二次线圈的互感，，k为耦合系数。

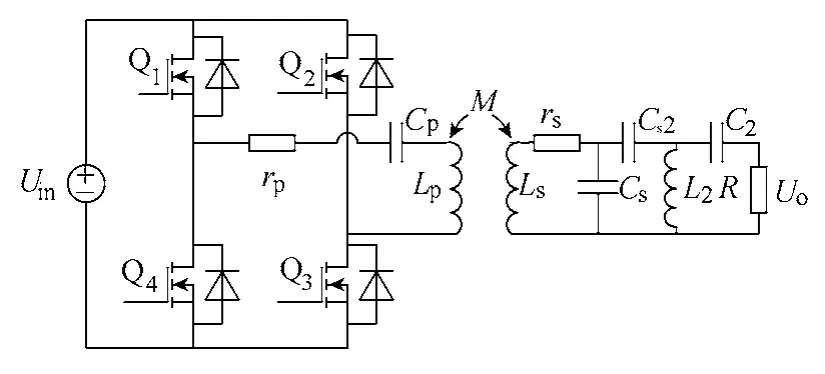
图1 系统电路结构Fig.1 System circuit structure

二次侧由接收线圈 Ls，并联电容 Cs，以及由Cs2、C2、L2构成的T型阻抗变换网络构成，其电抗关系为：

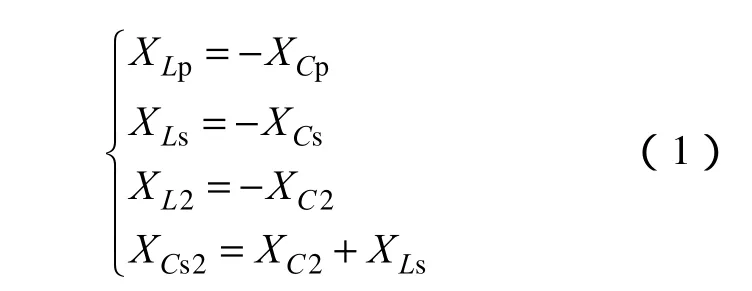
阻抗变换网络的加入使得二次侧等效为串联谐振，且具有更大的谐振容量。需要注意的是，模型中的rp、rs不能忽略，因为谐振时电流很大，即便很小的线阻也会对效率产生较大的影响。下面将对该结构详细分析。

2.1 阻抗特性分析

二次侧的阻抗变换如图2所示，Uoc是二次线圈感应的开路电压。谐振频率且Ls＜ L2，记，则有

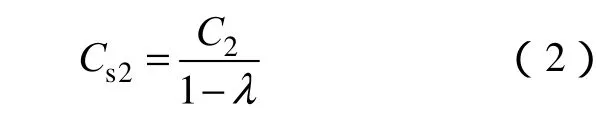
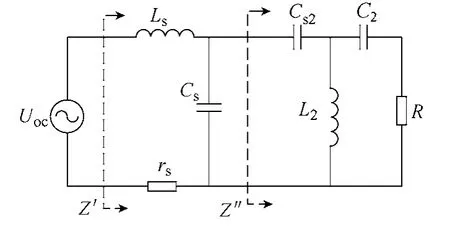
图2 二次侧电路的阻抗变换Fig.2 Impedance transformation of the secondary circuit

负载R经阻抗变换网络后记为Z′，并将其实部和虚部分开

因此Z′可以等效为电阻和电感 Ls的串联。进一步计算副边的总阻抗Z′，则有：

二次侧电路谐振时的品质因数为

与传统的二次侧串联结构相比，所提出的结构负载变为原来的λ2倍，提高了二次侧Q值，增强了接收端的谐振，从而使其更加适应弱耦合 ICPT的应用。实际上，能实现这种变换的组合有四种，而本文所提出的是一种使用电感个数最少的组合，因为在实际中，电感往往体积较大，采用这种结构最为实用化。

进一步的，将二次侧阻抗等效至一次侧，设Zr、为副边到原边的反映阻抗，则有

则逆变桥输出端的总阻抗Zin为

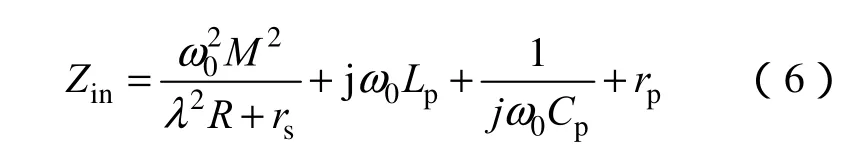
当工作于谐振频率时，Lp的感抗和Cp的容抗相互抵消，Zin仅有实部，因此耦合系数与负载变化将不影响谐振频率，采用这种结构的无线电能传输系统具有较好的频率稳定性，可以以定频的方式工作。

2.2 电路模型分析

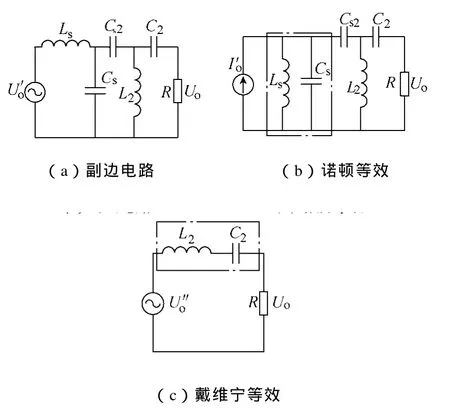
图3 二次侧电路等效变换Fig.3 Equivalent transformation of the secondary circuit

下面依据上述电路变换，对系统的输出电压增益与效率进行分析。

2.2.1系统增益计算

由图3b和图3c的变换过程，可以得到输出电压的表达式

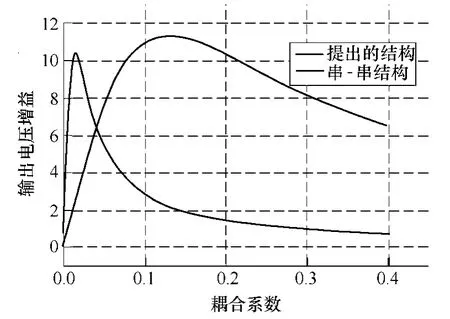
图4 两种结构增益对比Fig.4 Gain comparison of the two structures

将上述表达式中的λ2R用R代替，就变成传统串-串结构的增益表达式。对比所提出的结构与串-串结构的增益，如图4所示，在耦合系数较低时，所提出的结构增益大于串-串结构，这意味着采用该结构可以传输更远的距离。

由式（8）和图4可知，负载R与增益成正比，而当负载一定时，耦合系数增大的过程中存在一个增益极值点。式（8）对 M求导，令其等于 0，得到增益极值点对应的耦合系数为

最大增益为

由式（7）还可以得到负载电流与一次线圈电流的关系

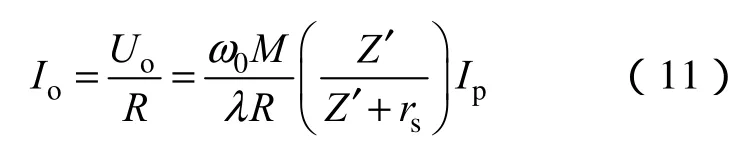
而二次线圈的电流与负载电流的关系为

因此一次线圈与二次线圈的电流比

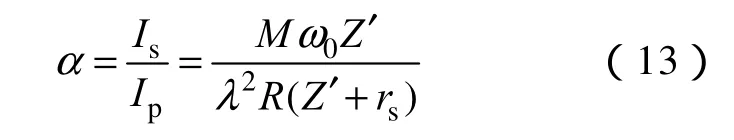
可以看到，采用这种结构的原副边线圈电流放大比与耦合系数成正比，且随λ的减小而增大。实际上由式（5）可知，参数λ选择越小，二次侧电路Q值越大，谐振电流越大。

2.2.2系统效率分析

设一次侧效率为ηp，二次侧效率为ηs，则有

系统总效率 η =ηpηs。将Zr、Z′的表达式代入式（14）有

由式（15）可知，一旦系统参数确定了，ηs就为一定值。随着耦合系数增大，反映阻抗增大，因此ηp升高。将上述表达式中的λ2R用R代替，就变成传统串-串结构的效率表达式。对比所提出的结构与串-串结构的效率，如图5所示：

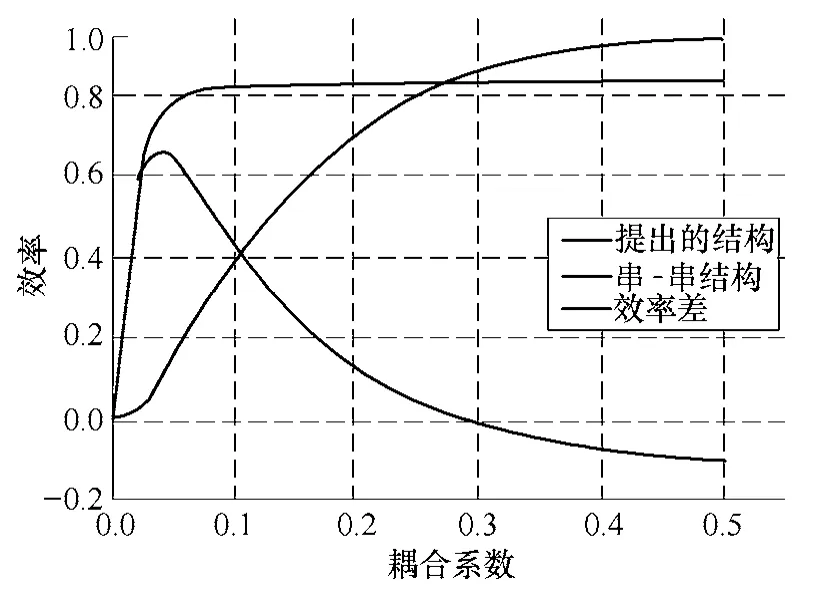
图5 两种结构效率对比Fig.5 Efficiency comparison of the two structures

可以看到，两种结构的效率均与耦合系数成正比。在耦合系数较低时，所提出的结构效率明显高于串-串结构，而当耦合系数较高时，串串结构的效率更高，因此所提出的结构更适合于弱耦合应用。可以求出效率差的过零点对应耦合系数为：

即实际中耦合系数0＜k＜k0时，更适合采用这种结构。

3 仿真与实验

3.1 仿真

使用PSPICE仿真，从频域分析电路相关特性，所采用的参数如表1所示。

表1 仿真选取的参数Tab.1 Parameters for simulation

电压增益的幅频特性随耦合系数的变化如图 6所示，随负载变化的曲线如图7所示。从图中可以看到，在谐振频率处，随着耦合系数增加，增益先增大后降低，由于采用该结构提升了Q值，在耦合系数 0.1时已经开始出现频率分叉现象。而增益与负载大小成正比，这与前面的分析一致。

图6 耦合系数变化时增益的幅频特性Fig.6 Frequency characteristics of gain with variation in k

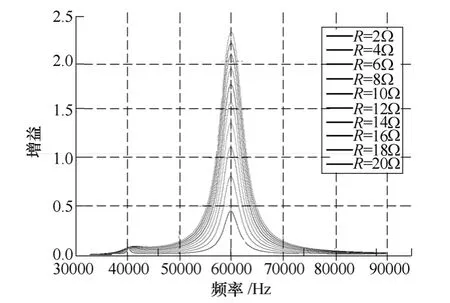
图7 负载变化时增益的幅频特性Fig.7 Frequency characteristics of gain with variation in the load

逆变桥输出端的电压电流相位差随耦合系数的变化如图8所示，随负载变化的曲线如图9所示。从图中可以看出，在谐振频率点，相角始终为零，谐振频率不随耦合系数与负载的变化而改变，具有较好的频率稳定性。

图8 耦合系数变化时逆变桥电压电流相角Fig.8 Phase angle between voltage and current with variation in k

图9 负载变化时逆变桥电压电流相角Fig.9 Phase angle between voltage and current with variation in the load

3.2 实验

为验证所提出的二次侧拓扑，搭建实验平台，如图10所示。一次侧与二次侧均为直径30 cm的圆形线圈，采用 litz线绕制以降低趋肤效应，原边匝数为6，副边匝数为5。两线圈从距离40 cm到距离10 cm时对应的耦合系数如图11所示。

图10 实验平台Fig.10 Experimental platform

图11 耦合系数与距离的关系Fig.11 Coupling coefficient in different distance

逆变电路为全桥，开关管选用IPW60R041C6，其导通电阻为41 mΩ，系统谐振频率 f0=60 kHz，R=12 Ω，λ=0.1。二次侧分别采用所提出的结构和传统串联结构，测量距离从10 cm到40 cm变化时的效率与输出电压增益，分别如图12和图13所示。

可以看到，在耦合系数较低时，所提出的结构相比传统串-串结构有较大优势，采用这种结构的接收端，可以传输更远的距离，且效率更高。

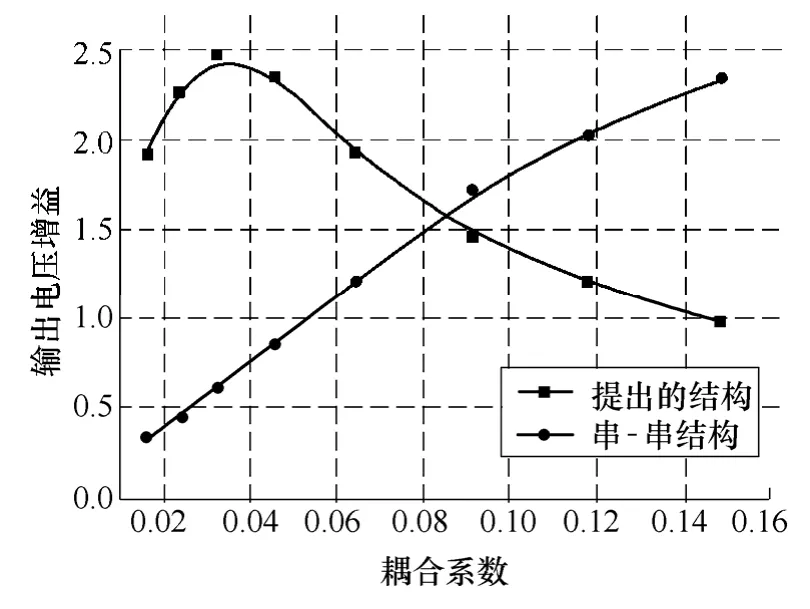
图12 两种结构传输效率对比Fig.12 Efficiency comparison of the two structures

图13 两种结构输出电压增益对比Fig.13 Comparison in output voltage gain of the two structures

4 结论

本文提出一种用于磁耦合谐振式无线电能传输的新型二次侧谐振补偿拓扑，并从阻抗特性与电路模型角度进行分析，给出其输出电压增益与效率的表达式。使用 PSPICE进行频域仿真并搭建实验验证平台，结果表明所提出的结构具有较好的谐振频率稳定性，并且在耦合系数较低时，传输性能相比较传统的串-串结构具有明显优势。值得注意的是，所提出的结构仅针对二次侧，而一次侧同样可以采用LCL、CLC等复合谐振结构以获得更好的传输性能，这也是下一步即将开展的研究工作。

[1] G N.Shinohara.Power without Wires [J].IEEE Microwave Magazine,2011,12(7):S64-S73.

[2] Kurs A,Karalis A,Moffatt R,et al.Wireless power transfer via strongly coupled magnetic resonances[J].science,2007,317:83-86.

[3] Litvak E,Foster K,Repacholi M.Health and safety implications of exposure to electromagnetic fields in the frequency range 300Hz to 10MHz [J].Bioelectromagnetics,2002,23:68-82.

[4] 武瑛.新型无接触供电系统的研究[D].北京:中国科学院研究生院（电工研究所）,2004.

[5] 田勇.分段导轨模式的电动车无线供电技术关键问题研究[D].重庆:重庆大学,2012.

[6] Dieckerhoff S,Ruan M J,Doncker R W De Design of an IGBT-based LCL-resonant inverter for highfrequency induction heating[C].IEEE Industry Application Conference.1999,3:2039-2045.

[7] 戴欣,余奎,孙跃.CLC谐振型感应电能传输系统的H_∞控制［J］.中国电机工程学报,2010,30(30):47-54.

Dai Xin,Yu Kui,Sun Yue.Study on H_∞ control method for CLC resonant inductive power transfer system[J].Proceedings of the CSEE,2010,30(30):47-54.

[8] Villa J L,Sallan J,anz Osorio,J F,et al.Highmisalignment tolerant compensation topology For ICPT system[J].IEEE Transactions on Industrial Electronics,2012,59(12):945-951.